应用思维导图，促进学生数学学习的能力提高

邓丽萍

摘要：数学是一门非常注重学习方法的学科，好的学习方法是提升学生学习效率和兴趣的关键。对于零零散散的知识点要善于总结归类，在归纳的同时进一步加深对知识点的记忆，更有利于今后的知识掌握和复习。而思维导图就可以很好的帮助学生归纳总结，整合数学难点，让学生掌握数学知识点之间的关系。

关键词：初中数学;思维导图;有效学习

数学思维导图以某关键词为中心，将与之关联的内容连接起来，帮助理清各知识点之间的关系。在理清各知识点内容时，可以把零散的内容绘制到一起形成系统性思维。从不同方向或角度制作数学思维导图，绘制的内容与结果往往是大不相同的，可以充分體现制作者的思考方向、特点等，与此同时也便于查验知识点。思维导图需要提炼内容的关键词，根据关键词的概括将环环相扣的知识点连接起来，从侧面提升抽象能力及概括能力，思维导图上下级节点之间会存在隶属关系（包含/被包含），没有隶属关系自然构不成上下层级关系，需要思考上下层级之间是否有能构成关系，可以用来培养逻辑思维能力。那么应用数学思维导图的作用及促进初中数学学习的优点有哪些呢，下面作具体阐述。

一、数学思维导图的作用

数学是数字与图形结合的一门学科，思维导图的作用及优点不仅能够有效地帮助孩子学习数学，能提高数学成绩，而且能扩散数学逻辑思维，增强分析解决问题的逻辑思维能力，进而带动其它学科成绩的快速提升，让学生的一生受益匪浅。数学思维导图由颜色、线条、图形、联想和想象五要素组成，数学思维导图的研发和使用，正是切合了数学本身的特点和数学对学习者的作用。

数学学不好主要体现在：学生理解力差，老师讲的内容没有弄明白;学生上课开小差，忽视了老师讲课的内容，而又碍于面子没有去请教老师和同学;还有学生没有找到学习乐趣厌倦数学科目，不喜欢学习数学。这种学习压状态抑了学生的兴趣和热情，严重影响了学生思维和能力的发展，初中学生知识学得越多，笔记记得越多，思维反而更易混乱。

这时候需要帮助学生树立一个正确的价值观，找到好的学习方法，养成良好习惯，数学其实是可以很简单的。所以转变学生的学习方式，把学习过程变得个性化，使学生的学习方式变成自主式、主动式、探究式，合作式尤为重要。思维导图更注重培养学生的逻辑思维能力，寻找知识之间的联系，建构知识体系和网络。在提高学生自主学习、合作交流能力的同时，学会将思维导图的思想方法尽可能多的应用于生活和学习的各方面，有利于提高学习和生活的效率。

二、思维导图促进初中数学学习作用分析

（一）应用思维导图，让学生积极开展课前预习

学习初中数学，一些学生往往难以形成自主预习的学习习惯和学习能力，这也就造成了数学教学课堂和学习效率的低下。面对这样的情况，教师可以构建预习思维导图，让学生积极开展课前预习。通过思维导图这样的方式，学生不仅能够衔接数学中的各个知识点，而且还能够深刻明确初中数学课程的学习目标和学习方向，在持续不断的训练当中养成课前自主预习的学习习惯、数学教师应根据有关规定，设计教学计划，通过前面而综合的观察学生们的数学学习情况，安排学生的预习计划和训练计划。通过这样的方式，来充分保障学生能够有计划并且有效率的学习新的数学知识，避免学生被落下。

例如，数学教师在讲解有关“圆”的知识时，可以先通过设计思维导图的方式，带领和引导学生进行学习，运用这种方法帮助学生主动预习和了解有关圆的基本性质、相关概念、弧长、面积、圆心角等的知识。通过运用思维导图这种教学方法，可以让学生准确无误的了解这节数学课需要把握好的重难点知识，然后再让学生掌握知识的清晰脉络和各个知识间的相互关系和相互联系，依据思维导图来制定数学课程的有关学习计划和学习方向，根据思维导图将学习到的数学知识点进行有效整理和整合。对于圆问题的解答前，同学们可先结合自己学习内容，制作关于圆的思维导图，完善圆的知识结构，然后再进行解题，便会提高解题的正确率。关于圆知识点的思维导维导图如下图。

例题：如下图，圆O的直径为AB，CB、CA与圆相交于点D、E，DC=DB，过点D作圆O的切线，与直线AC相交于点F。（1）证明：FD⊥CA;（2）若圆O的直径为10，∠FDC为30°，求DB对应的弧长。图4分析：第（1）问，分析问题与条件，问题为求证FD⊥CA，根据问题所需，分析条件DC=DB、D为切点。以此开展想象，因为在△ABC中，O点为圆心，DC=DB，所以点O和点D是三角形的边AB和BC的中点，所以OD为△ABC的中位线，再结合D点为切点，可以证明FD⊥CA。第（2）问，分析问题与条件，问题是求BD的弧长，条件为∠FDO为90°、∠FDC为30°，半径为5。以此扩展想象，根据条件可得△OBD为等边三角形，然后根据弧长公式解得答案。在此制作的思维导图（如下图）。

解：第（1）问，连接DO，因为DF为圆的切线，所以FD⊥DO，所以∠FDO=90°。又因为DC=DB，AO=BO，可得OD是△ABC的中位线，OD与AC平行，∠FDO=∠DFC=90°，所以直线DF和AC垂直。第（2）问，因为∠FDC为30°，∠FDO为90°，可求出∠BDO为60°，所以△BOD为等边三角形，∠BOD为60°，根据弧长公式，求得BD的弧长为。

（二）应用思维导图，提高解题效率和正确率

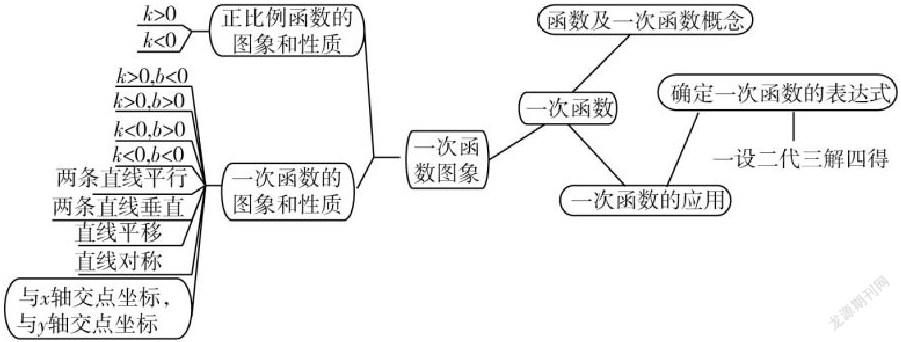
在数学解题过程中，运用思维导图可以有效发散思维，帮助同学们找到问题的关键，然后开展诊断性学习。像如在学习函数知识时，可以借用思维导图的展示，结合题目中的问题与条件，探索问题解答过程，发挥思维导图的重要作用，帮助学生快速提高解题效率和正确率。首先，展示一次函数的断维导图（如下图），结合例题通过思维导图寻找解题条件，帮助学生快速求解答案。

例题：甲、乙两车匀速从A地向B地出发，甲车行驶1小时后乙车出发，乙车到达B地休息1小时后原路返回直到与甲车相遇。甲车的速度为80千米/时，甲、乙两车的距离y（千米）与乙车行驶时间x（小时）之间的函数关系如图（如下图）。

分析：此问题以题目为中心制作思维导图，写出已知条件与问题，已知条件即甲车先出发1小时、甲车的速度为80千米/时、乙车行驶2小时与甲车相遇、乙车行驶6小时后在B地停留1小时再返回.问题即乙车的速度、H点坐标、m和n的值。根据甲车先出发1小时，再过2小时与乙车相遇，由此可求出乙车的速度.根据已知的乙车行驶速度与时间，求出A、B两地的距离.H点坐标的求解，可结合甲车速度、乙车到B地停留1小时，求出甲、乙两车经过n小时相遇.解：根据图象可知乙车行驶2小时后与甲车相遇，再结合甲先出发1小时，可列等式80×3=乙车速度×2，由此可得乙车的速度为120千米/时.又因为乙车行驶6小时到达B地，得到A、B两地相距120×6=720（千米），所以点H的坐标为（7，80），m的值为160，由此可求得。

此类问题的解答从思维导图寻找解题条件，再结合图象即可求出答案。

（三）应用思维导图串联知识点，提高學习能力

在初中数学的学习过程中，虽然单个的知识点非常容易被学生理解、记住和运用，然后加以实践。但是如果进一步将学到的所有知识点进行汇总，然后把它们通通堆放在一起，那么这些知识点就会变得非常复杂和难以理解。如果想要让学生对这些复杂的知识点进行有效记忆和实际运用，数学教师就可以采用思维导图的这种教学方式，用思维导图将每一个相互关联的知识点连接起来，有利于学生对知识点进行掌握和记忆，也非常有利于学生对于知识的理解和运用。

例如，数学教师在讲解三角形的相关知识点、圆的相关知识点、函数的相关知识点的时候，就可以运用思维导图给学生进行讲解，运用思维导图可以让学生清楚地知道、理解和掌握每一节知识内容的主要知识点和次要知识点，然后设计出主干和分支，将知识点逐步分层。在绘制思维导图时，教师要指导学生，引导学生制作思维导图，通过次用思维导图这样的教学方式，学生之间不仅可以相互交流、沟通、研究和讨论。

在学生逐渐熟练的掌握思维导图绘制的方法技巧和要点之后，数学教师就可以让学生们慢慢试着逐渐扩大有关知识点的网状结构和联系范围。例如，数学教师可以让学生把有关圆和三角形的相关知识点联系和结合在一起，将二次函数和一次函数的知识点结合在一起。这样就可以让初中数学所要学习的知识点更加简单和明了，也强化了初中数学各个知识之间的相互联系。通过制作思维导图，可以锻炼学生的逻辑思维能力，增强学生把握、回忆和连接数学知识的能力，进而提高初中学生应用数学知识的能力。

三、结语

综上所述，在初中数学教学过程，无论是对学生的解题过程中，还是新知识点的学习掌握，又或是复习总结，运用思维导图可以有效发散思维，帮助同学们找到问题的关键，然后开展诊断性学习。通过思维导图对知识点的展示，结合题目中的问题与条件，探索问题解答过程，发挥思维导图的重要作用。能快速的串联各知识点让学生快速理解新知识，有效的辅助学生学习和复习效果。

参考文献：

[1]贺佳.思维导图在初中数学解题中的应用[J].科学咨询（教育科研）.2020（04）.

[2]赵亚军.思维导图在初中数学教学中的有效性[J].数学大世界（上旬）.2021（04.

[3]吴佩俊.关于构建初中数学高效课堂的几点思考[J].数学学习与研究.2019（23）.

注：本文系南宁市教育科学“十三五”规划2019年度课题《应用思维导图，促进学生数学学习能力的提高》（课题编号：2019C774）阶段性研究成果.