随机需求与机会约束下多源联合选址-库存-定价问题研究＊

■ 崔竞 曹云植

中国科学院大学经济与管理学院 北京 100190

0 引言

随着人们经济水平的提高，市场需求不断多样性化，在供应链管理库存中，由不确定因素带来的供应链波动性产生的影响日益上升，越来越多的学者将其考虑到模型中，Tang[1]从产品供应管理、产品管理、信息管理等方面的不确定性做了深入研究；Prater E 等[2]构建了高度敏捷供应链，分析其对于不确定性的影响，发现目前并没有完全消除不确定因素的方法，只能缓解不确定因素的影响。为缓解不确定中断带来的影响，Zhu 和Cao[3]建立两阶段随机规划模型，并提出相应的分解算法进行求解。在不确定需求背景下，针对多产品产能约束的网络设计问题，Sarayloo等[4]建立了两阶段随机规划模型，并提出一种基于启发式学习的算法进行求解。在血液供应链中，针对不确定需求和血液的易腐性，Deh‐ghani 等[5]运用随机规划模型提出了血液供应链中的主动转运策略，运用算例证明了该策略能有效节约成本。

经典的供应链决策系统由战略、战术及运营层组成，针对各层面的独立决策管理问题已有深入的研究，例如在库存管理方面，徐贤浩等[6]提出库存商品价值变化情况下的库存决策问题；Mitra 等[7]对报童问题进行拓展，将销售期分为日常与倾销期，在周期末对剩余库存打折出售，对需求分布做出不同假设，提出了三种模型进行求解；Guo 等[8]以短生命周期产品为研究对象，在不确定需求下求出不同情况的最优订货策略。但将供应链各层面问题进行联合建模决策的文章还较少。Amiri-Aref 等[9]处理了不确定需求下多梯度供应链网络中选址-库存问题，采用情景迭代与样本均值结合的方法进行求解；Pirkul 等[10]采用拉格朗日和启发式算法求解相应库存决策问题中建立的混合整数规划模型，王林等[11]在选址-库存模型中考虑了资源约束与数量折扣，运用改进的自适应差分算法对模型求解。

研究不确定环境下供应链联合决策问题时，大多学者只单独考虑某种因素，例如需求、供货提前期等，本研究以整体收益为目标函数，同时考虑不确定需求与价格及其相关关系，建立单/多周期下两阶段随机规划模型，联合决策选址-库存-定价问题，采用遗传算法GA与粒子群算法PSO 分别求解，并对结果进行比较分析。本研究是国家自然科学基金重点项目“大数据驱动的高速铁路高可用性研究”的阶段性成果之一，主要针对在大数据背景下，面对不确定需求，运用随机规划的方法解决供应链网络中的联合选址-库存-定价问题问题。

1 问题描述

市场环境中，同一需求地可有多个供应来源，在两阶段联合选址-库存-定价问题决策模型中，第一阶段确定供应地选址问题；第二阶段确定供应地至需求区运输、库存及定价问题。模型考虑时间条件（单/多周期）、随机环境（确定/不确定）以及随机变量（需求和价格）等三维影响因素下的6种工况，即为图1中1～6结点对应的情况。

图1 6种决策工况说明图

1.1 模型参数及变量说明

本研究模型参数及变量说明如表1。

表1 模型参数及变量表

1.2 随机需求

需求不确定时，建立随机机会约束条件，采用蒙特卡洛逼近概率运用大数定律的思想求解，对于P{f(x) ≤β}，通过随机数或者伪随机数给出N次f(x)的值，其中共有M 次f(x) ≤β，由大数定律可知，当N 足够大时，M/N 可以作为P{f(x) ≤β}的近似值[12]。运用随机数给出N×N个f(x)的值，放入矩阵Z 中，对矩阵Z 每列进行从小到大排序，从每列中选第N×β个值求平均数，作为概率约束条件中的需求值。

1.3 随机价格

模型在考虑随机价格与需求之间关系时，构建产品与需求之间为线性函数[7]为：

Qj=b-a×Pj

添加缓冲变量为ω，即函数式变为：

Qj=b-a×Pj+ω

假设参数b、a、ω服从于正态分布函数，则价格推导过程为：

（1）收益函数为：

W=Qj×Pj=(b-a×Pj+ω)×Pj

（2）收益期望值为：

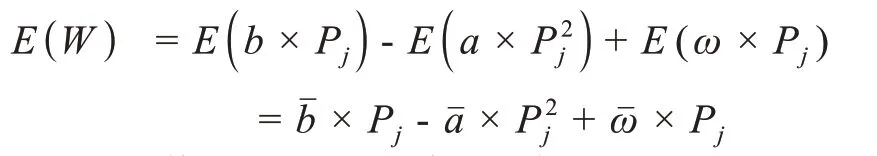
（3）期望值函数对价格求导，令导数为零，得初始价格为：

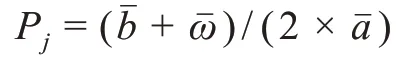
2 问题建模

2.1 问题假设

本研究建立多源联合选址-库存-定价问题决策模型，对库存配送网络系统做以下条件假设：

（1）每个需求区需求服从正态分布并相互独立；

（2）考虑价格与需求关系时，两者成反比关系；

（3）需求区物品可源于不同供应地；

2.2 收益及成本说明

（1）销售收入Z1为：

（2）供应地固定建造成本Z2为：

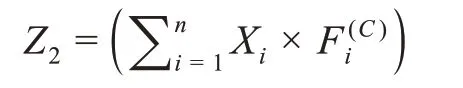
（3）需求地存储成本Z3为：

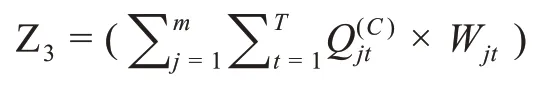
（4）结余成本（未销售的产品成本）Z4为：

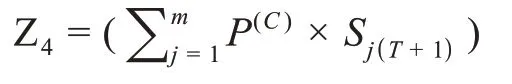
（5）缺货成本Z5为：

（6）运输成本Z6为：

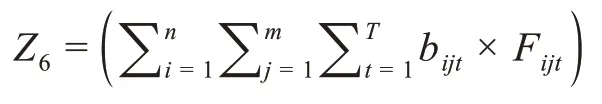
（7）采购成本Z7为：

（8）最后一周期倾销收入Z8为：

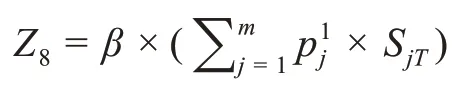
2.3 建立目标函数及约束条件

以整体收益为目的，将供应地固定建造成本、需求区运输成本、仓储成本等考虑到模型中，建立如下目标函数及约束条件：

约束(1)表示当Y= 0时，产品价格确定，该约束表示各周期无缺货现象，满足顾客需求。约束(2)表示当Y=1 时，产品价格不确定，引起顾客需求不确定，建立概率约束条件，顾客服务水平为85%。约束(3)表示t周期末需求区j的缺货量。约束(4)表示周期t内存储量由前一周期剩余量和需求区的配送量组成。约束(5)表示需求区t周期末剩余量。

3 算法设计

本研究建立了不确定需求与价格下机会约束随机规划模型，为解决机会约束条件，即约束(2)，遂将蒙特卡洛法与启发式算法进行结合，具体流程见图2。

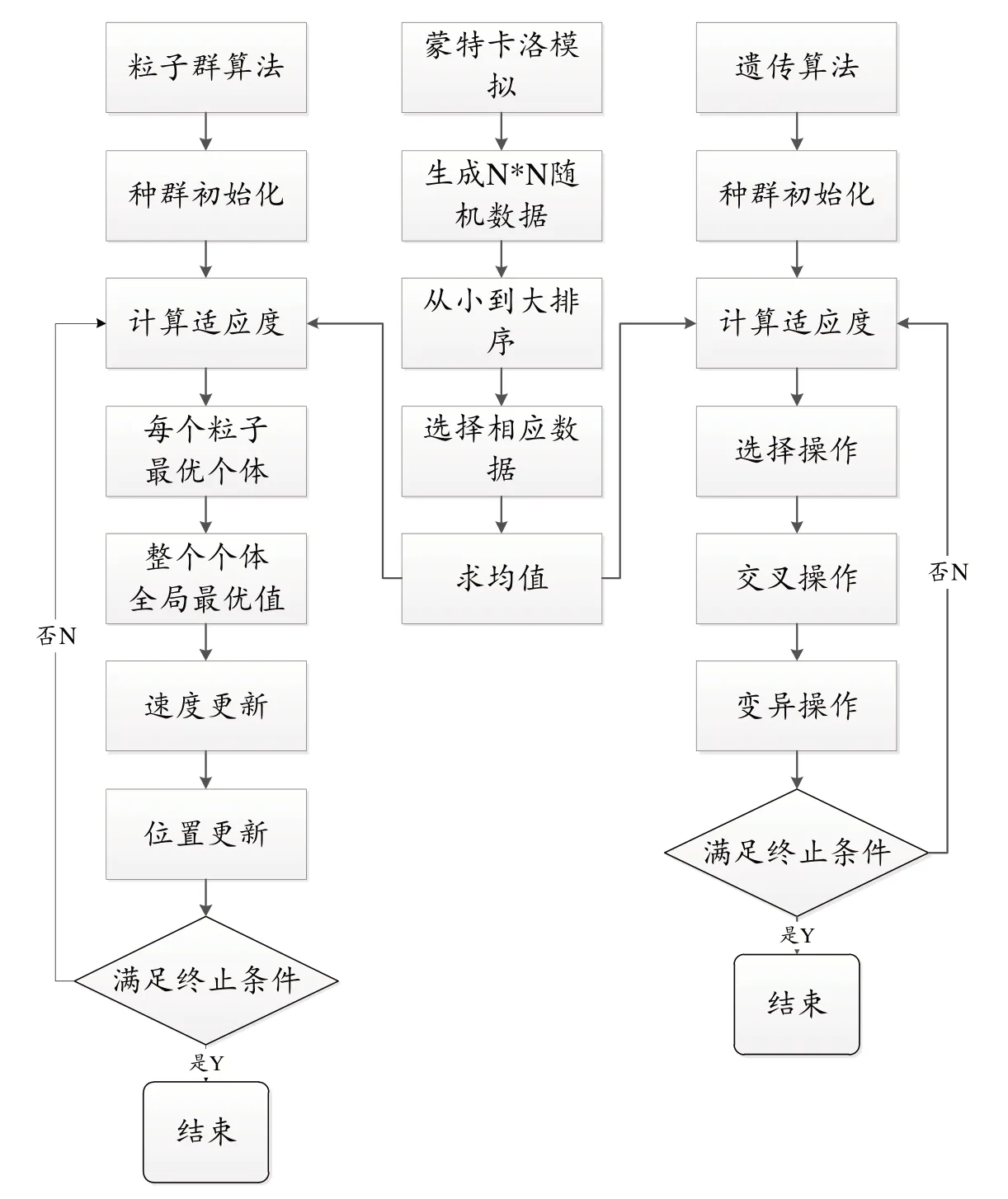
图2 求解算法流程图

3.1 遗传算法与粒子群算法准备过程

遗传算法与粒子群算法前期准备过程类似，主要包括参数初始化、确定种群编码方式等。

3.1.1 前期参数初始化

对遗传算法中初始种群数、进化次数、交叉变异率和粒子群算法中初始种群规模、进化次数、学习因子、速度范围等参数进行初始化，确定前期所需要的数据（表2）。

表2 算法初始参数数据

3.1.2 种群编码方式

本研究将决策变量按顺序引入同一矩阵中，对于决策变量Xi，编码方式为二进制编码，其余决策变量按照变量范围与随机概率的积作为变量的值，使得数据能够相对均匀的分布在范围内。

3.1.3 选择适应度函数

本研究以整体收益作为目标函数和适用度函数，求解最优决策方案。

3.2 遗传算法执行过程

遗传算法中将生成初始种群、选择、变异、交叉作为主要操作过程。

构建初始种群：对已编码的染色体，一次性选择足够的数量生成初始种群。

选择操作：以适应度函数值为基准，从初始种群中选择一定数量的个体作为新种群，采用轮盘赌选择法，计算出初始种群各个体适应度值，及其占总体的比率，得出个体被选择的概率和累计概率，通过随机数选择个体，重复N次后产生优势个体群。

交叉操作：任选两个体，产生随机数与给定的交叉率进行对比从而确定是否进行交叉操作，若进行交叉，选择相同位置基因进行交叉，见图3，否则返回原始个体。

图3 交叉和变异操作示意图

变异操作：变异操作为提高算法的全局搜索能力，以避免落入局部最优解。变异时先任选个体，判断是否变异后，产生随机数确定不同的变异操作。

终止操作：设定进化代数判断算法是否终止。

3.3 粒子群算法执行过程

粒子群算法执行过程包括速度与个体更新。

（1）速度更新

在粒子群执行过程中，粒子飞行速度(=(vi1,vi2,vi3…vis)）会根据上一种群中的全局最优值和个体最优值进行优化，具体操作如下：

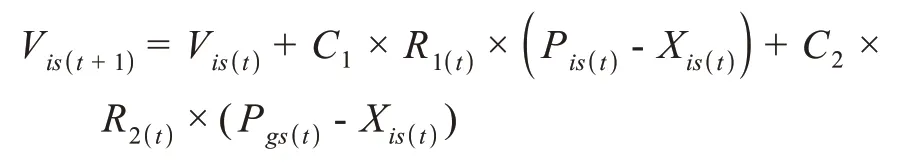
（2）个体更新

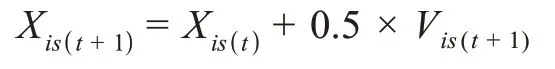
4 算例

4.1 数据

本研究以X 公司单/多周期两阶段联合选址-库存-定价为例，共有2 个供应地，3 个需求区，分别记为i1、i2,j1、j2、j3，单周期的T取1，多周期T取3，供应地固定建造成本为100，需求确定性模型中需求地需求分别为70,86,93，价格确定模型中销售价格为50，其余数据见表3、表4，分别求解6 种工况（图1 中1～6 结点对应的情况）的模型，即单/多周期下确定需求与价格、随机需求与确定价格以及随机需求与不确定价格模型。

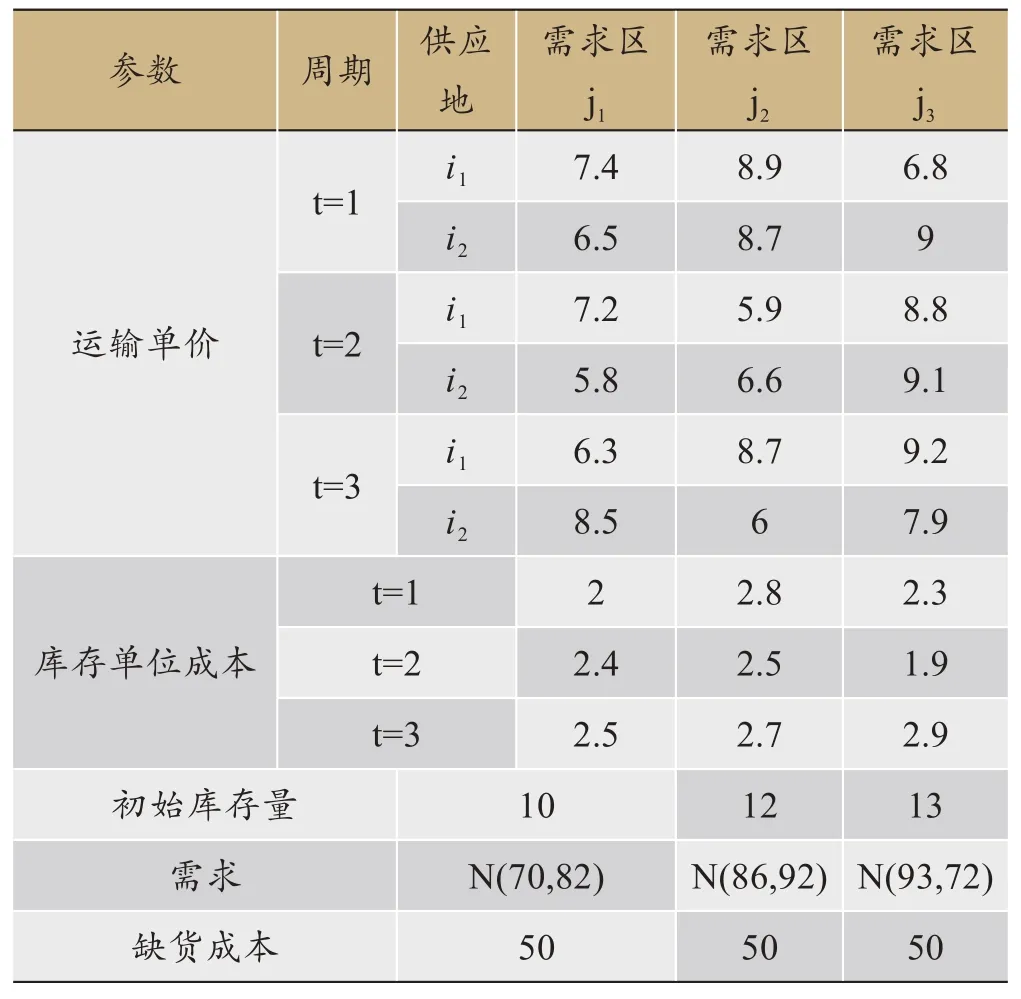
表3 价格确定性模型初始数据一览表

表4 价格不确定性模型数据

4.2 结果

根据上述模型及初始数据，分别用遗传算法（GA）与粒子群算法（PSO）MATLAB 自主程序求解，得到6 种工况下结果及适应度值，计算结果与收敛结果见图4。

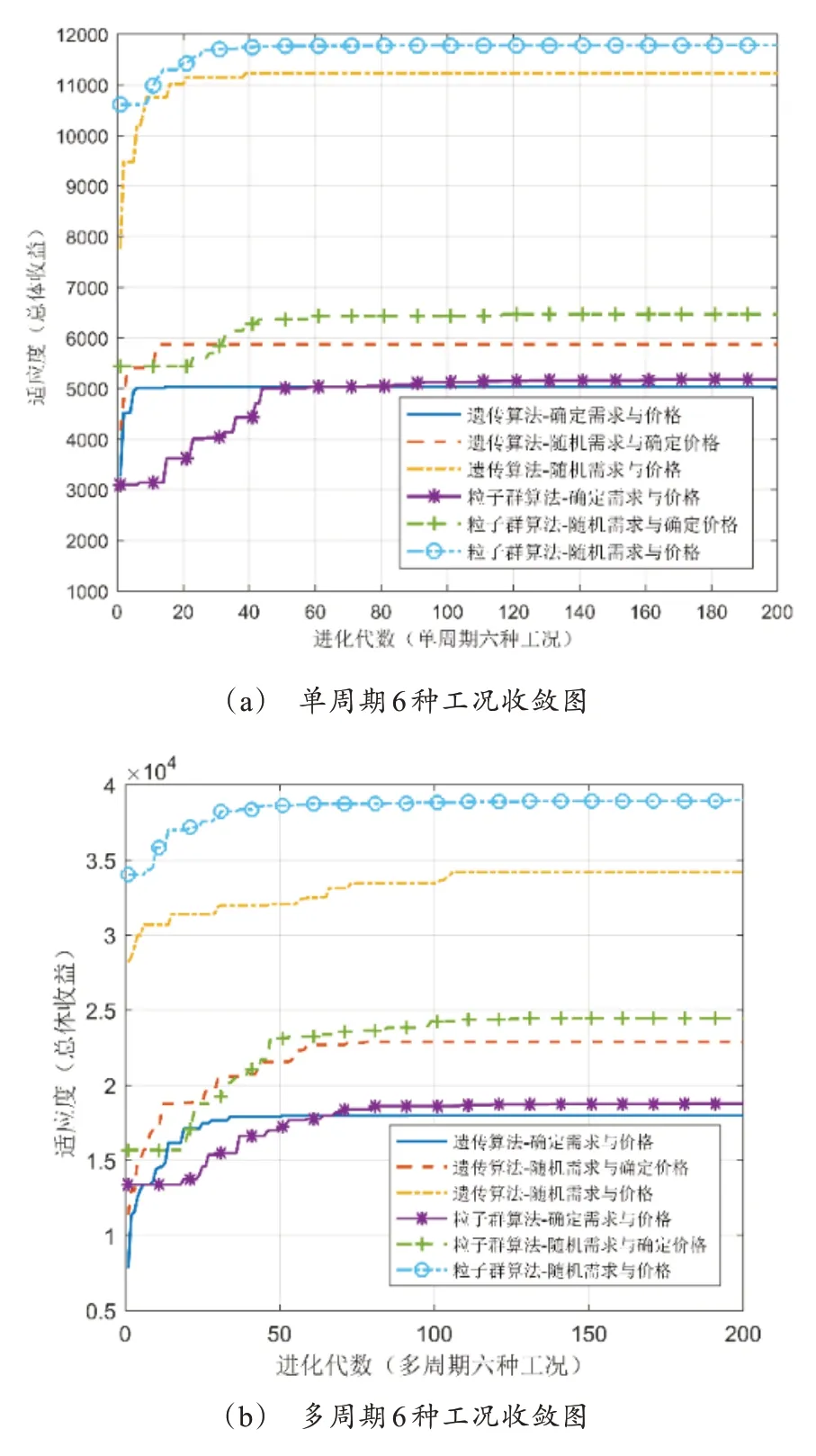
图4 单/多周期算法收敛图

5 结果与算法对比分析

5.1 不确定模型与确定模型结果对比

随着不确定因素（需求和价格）的逐步引入，产品总体收益不断上升，尤其将两种不确定性因素同时引入到模型中，适应度值有了明显的增加，首先，不确定需求更真实模拟了供应链中由于顾客、环境等因素导致的市场不稳定现象；其次，本研究在考虑价格不确定时，存在产品倾销期，尤其是针对短生命周期产品，避免产品浪费，节约了成本，提高了供应链整体收益。

5.2 单/多周期结果对比

将单周期与多周期收益对比分析，以粒子群算法求解结果为例，多周期适应度值为3个单周期收益值和，取多周期适应度值的1/3，与单周期比较，在确定需求与价格、随机需求与确定价格、随机需求与不确定价格3种工况下，将单周期数据与多周期数据分别比较，见图5。对于每种工况，多周期均高于单周期收益。相较于单周期模型，多周期模型有效处理周期间库存的传递，考虑了由于供需不匹配导致的库存积压问题，将多周期库存问题引入到模型中可以更准确决策长期的订货问题，从而能够提高供应链整体收益。

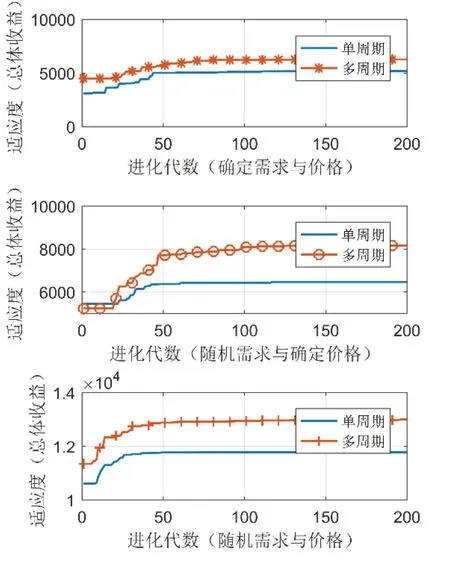
图5 单/多周期结果对比图

5.3 算法计算效果对比

针对每个模型，分别采用了遗传算法和粒子群算法求解最优决策结果，如图5，对比分析两种算法计算效果：（1）遗传算法的收敛速度略快于粒子群算法。（2）粒子群算法的最优适应度值总是略高于遗传算法。因此，针对不同的情形应采用不同的算法进行求解，例如，当不考虑运行时间，或运行时间重要性较低时，粒子群算法更适用于问题的研究；反之，若时间要求高，需要及时进行决策时，遗传算法更适合。

6 结论

本研究在随机需求与价格下，针对联合选址-库存-定价问题，建立机会约束随机规划模型，将单/多周期与不确定因素进行结合，求解出6 种不同工况下供应链整体收益及其决策变量。通过算例，比较结果得出以下结论：（1）模型中考虑产品周期性即周期间库存传递，相比单周期，在战略阶段选址问题中，多周期模型提供了更准确有效的决策，整体收益相较于单周期模型有所提高。（2）本研究应用了两种启发式算法，其中粒子群算法相比较遗传算法，针对本研究问题，收敛速度不如后者，但结果较优，若不考虑收敛速度与运行时间，粒子群算法更有效。（3）考虑不确定因素的收益结果优于确定型结果，尤其是同时考虑不确定需求与动态定价时，更符合市场情况，验证了随机规划模型的合理性。为随机环境下联合选址-库存-定价研究提供参考。

在供应链联合选址-库存-定价问题中，不确定性的因素带来的影响越来越大，本研究只在针对随机需求以及动态定价的背景下，分析了单、多周期的决策问题，未来可针对更多的不确定性问题进行研究，例如生产不确定性、供应中断不确定性、成本不确定性等。