军用装备运输振动环境：全息分析与再现

吴家驹 苏华昌 贺智国 贾亮

军用装备运输振动环境：全息分析与再现

吴家驹 苏华昌 贺智国 贾亮

（北京强度环境研究所，北京 100076）

本文讨论了军用装备运输振动环境的全息分析与再现方法。基于乘积模型的信号解调，将运输振动分解成载波和调制波，结合谱分析获得表征运输振动的关键特征参数，以此统计制定试验条件，同时给出了运输振动再现方案与保真度评价方法。通过多个案例的演示验证，该方法展示出广泛的适应性和灵活性，具有较好的应用价值。

疲劳损伤谱；高峭度控制;变烈度控制；谱密度控制；时间波形再现；全息分析；保真度

0 引言

按照军用装备环境试验标准，运输振动用功率谱定义的平稳高斯随机过程来表征。完整的环境条件取决于任务场景（包括路面类型、速度和距离）的详细规定。根据功率谱反演的时间历程进行序贯的单维随机振动试验，完成运输振动环境的模拟。使用功率谱表征运输振动环境需要几个假设。第一是时域的平稳性，即各种统计平均随时间的变化都非常缓慢；第二是幅值域的正态性，即振动幅值呈高斯分布；第三是在整个时间间隔内的振动可以用短样本的各种平均来描述，而没有过度的不确定性。然而实际的环境，却是非平稳非高斯的随机振动，而且多自由度同时存在。基于功率谱的平稳高斯随机振动试验方式，难以模拟实际环境中的高峰值和时变烈度；而单维序贯的试验方式，也不能模拟多自由度同时激励的影响。实际环境的高峰值、时变烈度和多自由度之间的相干特征，是造成传统方式试验结果的不确定性（“欠”试验）的主要因素。虽然可以通过增大功率谱密度值来“等效”高峰值和时变烈度的作用，不过所造成的“过”试验程度很难控制。业界一直在努力改进运输振动环境的模拟方式，新版美军标从军用装备运输振动环境的维度和正态性两个层面，来规划运输环境的模拟[1]。文[2,3]提出了基于外场实测数据的六自由度谱密度矩阵试验条件制定，并引入“峭度”参数作为补充试验条件的非高斯随机振动试验方法。文[4]提出用乘积公式作为分析运输振动的数学模型，将非平稳随机振动分解成功率谱表征的平稳载波和跌宕周期谱表征的调制波。文[5]则建议用时变烈度的分布函数表征调制波，文[6]提出兼顾分布函数和跌宕周期的非平稳随机振动的分析和综合方法，给出了适合控制仪器实现的试验条件制定步骤。上述研究成果可以用来处理任务场景详细规定的运输振动环境模拟。在实践过程中笔者发现只用功率谱不足以表征运输振动环境的全部特征信息，还需要引进新的参数。本文提出一种新的运输振动环境模拟表征方法，通过用方差谱、峭度谱、跌宕周期谱和累积分布函数四个关键参数来表征运输振动环境各自由度的内在信息，将提取这些参数的详细过程称为“全息分析”。结合当前可提供的振动试验控制算法，给出再现全息谱的方法，并用几个军用装备运输的实测振动时间历程，以改进的疲劳损伤谱为评判准则，通过虚拟试验演示验证了新的运输振动环境模拟方法的保真度。

1 运输振动的全息分析

谱分析是揭示随机数据统计特征的有效工具。传统上定义为时间频率转换的谱分析，是基于那些统计特征不随时间变化的平稳性假设，采用线性分解得到的。对于非平稳随机振动，单一的谱分析不足以反映整个过程的非平稳特征。最好的方法是除了需要记录波动幅度（能量密度）的分布外，还要用时间函数表示幅度的变化并能重现的全息分析。军用装备的运输振动环境是一个多自由度随机过程，每个自由度都明显地具有非平稳的属性。其特征可用承受基础运动激励的单自由度系统说明

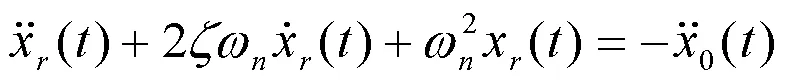
其中基础激励是随车速变化着的高低不平路面场

如果车速不变，那么基础位移对时间的导数

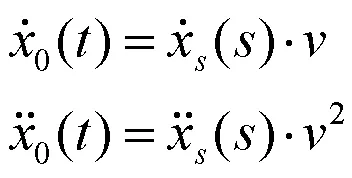
(4)式右端第一项是路面起伏对距离的导数，如果假设路面是平稳的，那么它也是平稳的。倘若速度不变，那么激励和响应都是平稳的，烈度正比于速度平方。多自由度线性系统的输入输出关系也是如此，只不过烈度正比于速度平方的关系不一定能维持

这个乘积公式称为乘积模型。式中wth的量纲与响应信号xth的相同，反映烈度随时间变化，称为调制波；th是根均方值为1的无量纲时间历程，称为载波。文[4]基于乘积模型的信号解调研究了时变烈度与时变车速（GPS测量）的关系。图1展示出车速与振动量值的相关性。前一时段的名义车速为15mph，时变车速的均值为16.05 mph，标准差为0.17，拟合速度指数为0.39；后一时段的名义车速为20mph，时变车速的均值为19.38 mph，标准差为0.23，拟合速度指数为0.62。其实，对于根据实测振动制定试验条件来说，指数的具体值并不太重要。

图1 车速与振动量值的相关性

依据运输振动产生机理，特定工况的实测信号能分解成平稳载波和缓变调制波。载波与调制波是两个彼此独立的随机过程，可以分别做统计处理。它们各自的幅值域和时域分布都对载荷信号的破坏潜能有重要影响。在以往的分析中，大多假定载波是具有高斯分布的平稳随机过程，只用“方差谱”表征就足够了。方差谱定义为分频窄带信号的二阶距。可是，很多符合平稳条件的外场测量信号的载波，总体计算的峭度也接近高斯分布值，但幅值分布却偏离高斯分布。这种平稳非高斯载波的定义，除了二阶距以外，还需要高阶距。其中最简单的是信号分频的四阶中心距，这里将其称为“峭度谱”。峭度谱定义为窄带信号的峭度，即四次中心距与二次距平方之比，为无量纲参数。这样，平稳载波时间维度的表征是方差谱，空间维度的表征是峭度谱。调制波通常是一个甚低频的随机过程，其时间维度的表征是跌宕周期谱，空间维度的表征是累积分布函数。至此描述运输振动环境的要素可以归纳为：载波的方差谱和峭度谱，调制波的跌宕周期谱和烈度的累积分布函数。这四组参数合起来才能比较完整地表征运输振动环境。图2是针对实测波形的数据处理流程，包括信号的解调和解调后信号的统计特征计算。

图2 实测运输振动信号分解流程

1.1 解调信号

有多种方法实现信号的解调[7]，其中滑动平均算法更容易规范化。按传统的韦尔奇周期图计算方法，取一帧时间波形(th)，计算其标准差。然后再取新的时间波形（重叠50%），做同样计算，直至信号结束。插值得到与信号等长的时变调制波(th)，原信号除以调制波形成平稳载波(th)。

1.2 统计特征

调制波跌宕周期谱分析的原理是认为一个缓变非负时间序列可用几个不同周期的正弦叠加而成。具体方法是先用调制波的自相关函数形成 Hankel 矩阵，然后通过奇异值分解所得的到奇异值和向量，计算跌宕周期和幅值相位[8]。时变烈度的幅值分布按通常的统计方法计算，或进一步用经典的概率分布函数拟合实测数据，获得简单的表征参数。载波方差谱和峭度谱的具体计算方法是先将原始信号带通（等带宽或对数等带宽）滤波，然后计算滤波后的窄带信号的方差与峭度。带宽要与信号的长度匹配，以保证谱的统计精度。

1.3 制定条件

以上是基于一种工况（同一路面、同一速度）测得的时间历程的统计分析，制定条件还要考虑不同工况（不同路面、不同速度）的特征参数统计。其中时变烈度在很多情况下适用对数正态分布，通过相平均制定试验条件；但形成跌宕周期谱的试验条件，用时平均算法为好，因为初始相位的差异，相平均可能会平均掉时域信号的强势分量。试验分析证明，输入信号的周期越长，响应越能维持分布的“尾巴”[5]。

图3是运输振动全息谱分析实例。第一行是外场实测时间历程（th）。第二行是原信号经滑动平均得到的解调信号，其中第一列反映烈度随时间变化的调制波（th），第二列是反映随机路面和车载系统耦合特征的平稳载波（th）。第三行是全息谱分析结果，其中前两列是分别从调制波提取出的烈度分布函数（PDF）和跌宕周期谱（RPS），反映受驾驶员控制的车速变化。后两列是分别从平稳载波提取出的方差谱（PSD）和峭度谱（KUS），反映路面起伏的分布和车载系统的非线性。

图3 运输振动全息谱分析实例

2 运输振动环境再现方法

虽然精确再现运输环境需要综合跌宕周期谱、烈度分布函数、方差谱和峭度谱四组参数，不过在环境再现的实际操作时，参数可以根据任务目的和控制设备能力来搭配选择。目前流行的单维随机振动试验，平稳高斯的用谱密度控制，密（SDC）模块实现，非平稳的用“时间波形再现”（TWR）模块实现。新近推出的变烈度控制，烈（VIC）模块实现非平稳随机振动试验控制。“高峭度控制”（HKC）模块实现平稳非高斯随机振动试验控制，模拟诸如运输振动中的瞬态振动和“炮震类”（搓板路、履带式车辆）振动。图4是运输振动信号综合框图。

图4 运输振动信号综合框图

图4的第一行是基于烈度分布函数生成平稳调制波流程。根据试验时间的长短，产生均匀分布随机数序列（0-1），逐个匹配时变烈度的分布函数的出现概率（0-1）所对应的烈度值，形成新的随机数构成的时间序列。在现行的技术标准中，处理非平稳数据的办法是分段平稳，用逆幂率实现时间缩比。也就是说，将烈度不同的分段平稳随机振动等效成单一烈度的试验条件。标准建议用逆幂率法则等效[1]

第二行是随机烈度序列按选定的跌宕周期重新排序，生成非平稳调制波流程；按跌宕周期谱、由多个正弦叠加形成相同长度的时间序列。将依据分布函数随机产生的时间序列，按照跌宕周期产生的时间序列重新排列（两者从小到大排列，前者位置移动到所对应的后者位置），得到既满足分布函数又满足跌宕周期的调制波。

第三行根据功率谱生成平稳高斯载波流程。传统的方法有两种：带通滤波和“逆韦尔奇”变换。

第四行是基于峭度谱生成平稳非高斯载波流程。将已满足方差谱的时间序列逐个进行窄带滤波，滤波后的信号经多项式变换，使其满足该窄带的峭度，然后将所有窄带信号叠加形成载波时间历程。根据同一组试验条件参数，可以重构出高斯和非高斯两类载波、平稳和非平稳两类调制波。调制波和载波可以有多种组合方式：高斯载波和平稳调制波组合适于谱密度控制，高斯载波和非平稳调制波组合适于变烈度控制，非高斯载波和非平稳调制波组合适于时间波形再现控制。不同组合方法所产生的效果并不相同，因而需要一个判断保真度的方法。可以参考传统基于输入谱的疲劳损伤谱方法，但需要改造才能适应非平稳载荷。

3 再现保真度评价方法

为了检查振动环境的模拟效果，或者比较实测振动环境两个工况的恶劣程度，需要建立一个有效的评价方法。振动所造成的破坏大体上可归为门槛型和累积型两类。在受到振动激励时，装备或因响应瞬时峰值过大，超过门槛值发生破坏；或因响应幅值的振动循环次数太多，造成累积损伤。响应的大小不仅取决于激励的烈度和分布，也取决于装备的品质因子，需要结合起来考虑。门槛型的通常用“冲击响应谱”击响应谱动来比较，累积型的则用“疲劳损伤谱”（FDS）来比较。两者都是基于基础加速度激励下，一组单自由度系统相对位移响应随系统固有频率的变化来描述（图5）。疲劳损伤谱描述了载荷信号作用于单自由度系统固有频率之间的关联，能准确反映载荷信号对实际装备的破坏能力。

图5 基础激励单自由度系统

根据疲劳损伤谱的基本原理，单自由度系统的应力与相对位移成正比。可使用标准的SN曲线，通过Miner线性损伤累计准则来计算累积损伤值。大多数情况下，人们并不关心某个信号的疲劳损伤谱的绝对数值，而只关心不同信号之间疲劳损伤谱的对比。对于多个载荷信号，只要采取相同的弹簧刚度系数和SN曲线截距，无论具体取值如何，疲劳损伤谱的比例关系维持不变。目前流行的“疲劳损伤谱”能表示成解析式，但是输入都是以功率谱的形式给出的[1]

利用该方法，可以对非平稳运输振动进行累积损伤计算，以此来评价对比不同模拟方法的保真度。

4 应用案例

第一个例子是前面讨论车速与烈度关系所用的数据，如图6所示。图6a）为车辆在同一路面行驶时，同一个测点测得的前后两段时间历程。传统做法是将它们看成“弱”平稳的，取相同时长，计算其整体的均方根值、峭度和波峰因子（表1）。对两段时间历程作深入谱分析，得到功率谱图6b）、概率密度函数图6c）和累积损伤谱图6d）。从图6可以看出，低速时段的累积损伤明显低于高速时段的累积损伤，符合常理，然而与之相反，表1所示低速时段的三个参数比高速时段更高，这说明用信号整体的均方根值、峭度和波峰因子来反映载荷的“潜能”未必确切。

图7～图10对应的四个案例，是几种不同类型运输振动环境的全息谱分析和基于相同参数的场景再现。其中图7～图9是火箭全箭轮式车辆运输时，不同工况下测量的车轴、车架和箭体振动信号及其综合效果比较。图10 是搓板路上结构振动信号综合效果对比。左图为时间历程，右上图为幅值概率密度函数，右下图为累积损伤谱。调制波的重构既计及烈度分布函数又满足跌宕周期要求；载波分别用功率谱按逆韦尔奇方法重构成高斯载波，和基于高斯信号的对数等带宽滤波后多项式变换形成的非高斯载波。最上面的图为原信号，排第二的图为非高斯载波和非平稳调制波的合成，排第三的图为高斯载波和非平稳调制波的合成，排第四的图为高斯载波和等效平稳调制波的合成。

纵观信号的累积损伤谱，各种重构方法都有很高的保真度。其中置顶曲线，说明全息复现的好处。两种基于高斯载波的相对简化方法，在应对车轴一类强烈非线性信号时就出现保真度下降情况。可以参照累积损伤谱，通过提高烈度的办法，来保证模拟的保守性。

图6 实测的运输环境损伤比较

表1 两种车速下的振动特征参数

图7 车轴振动综合效果对比

图8 车架振动综合效果对比

图9 箭体振动综合效果对比

图10 搓板路上结构振动综合效果

5 结论

本文提出了军用装备运输振动环境的全息分析与再现方法。基于军用车辆运行随机振动产生机理，用乘积公式作为装备运输振动的统一分析模型。通过滑动平均，将实测信号分解成平稳载波和时变调制波：载波用方差谱与峭度谱，调制波用跌宕周期谱与烈度分布函数作为表征参数。通过参数的不同组合可以形成不同的环境模拟方法，利用改进的疲劳损伤谱可以判断环境模拟的保真度。通过多个案例的演示验证，展示出该方法具有广泛适应性和灵活性。后续，将在如何折中规范的简约性与试验条件的保守性方面开展进一步研究。

[1] MIL-STD-810H. Department of defense test method standard: environmental engineering considerations and laboratory tests[S]. 2008.

[2] MIL-STD-1540c. Test requirements for launch[J]. Upper-Stage and Space Vehicles , 1994.

[3] NASA-HDBK-7005. Dynamic environmental criteria[S]. 2001.

[4] 吴家驹, 常洪振, 王求生. 军用车辆运输振动分析[J]. 强度与环境, 2018, 45(5): 1-6. [Wu Jiaju, Chang Hongzhen, Wang Qiusheng. Analysis of military vehicle transport vibration[J]. Structure & Environment Engineering, 2018,45(5): 1-6.]

[5] Rouillard V. The synthesis of road vehicle vibrations based on the statistical distribution of segment lengths[C]. 5th ACAM 2007 , Brisbane Australia.

[6] 吴家驹, 贺智国, 王璟南. 非平稳随机振动与烈度控制[J]. 强度与环境, 2019, 46(2): 1-6. [Wu Jiaju, He Zhiguo, Wang Jingnan. Non-stationary random vibration and intensity control[J]. Structure & Environment Engineering, 2019, 46(2): 1-6.]

[7] Bendat J S, Piersol AG, Random data Analysis and measurement procedures[M]. JOHN Wiley & SONS, 1990.

[8] 吴家驹, 贺智国, 付玮. 非高斯随机振动与峭度控制[J]. 强度与环境, 2018, 45(6): 1-6.[Wu Jiaju, He Zhiguo, Fu Wei. Non-Gaussian random vibration and kurtosis control[J]. Structure & Environment Engineering, 2018, 45(6):1-6.]

Military Equipment Transportation Vibration Environment:Holographic Analysis and Reconstruction

WU Jia-ju SU Hua-chang HE Zhi-guo JIA Liang

(Beijing Institute of Structure and Environment Engineering, Beijing 100076)

The holographic analysis and reconstruction of military equipment transportation vibration is discussed in this paper. Base on the product model of the signal demodulation, the characterization and spectrum analysis of the carrier and modulated wave is elaborated. The key parameters of transportation vibration are obtained, and the reconstruction scheme of and the fidelity evaluation method of transportation vibration environment are given. Through the demonstration and verification of several cases, this method shows a wide range of adaptability and flexibility, and has good application value.

Fatigue damage spectrum(FDS); High kurtosis control; Variety density control(VIC); Spectrum density control(SDC); Time wave reproduce(TWR); Holographic analysis; Fidelity

V416.5

A

1006-3919(2022)02-0057-08

10.19447/j.cnki.11-1773/v.2022.02.008

2021-08-25；

2021-12-26

吴家驹（1939－），男，研究员，研究方向：随机振动分析与试验；（100076）北京9200信箱72分箱.