四边固支复合材料矩形平板轴压失稳的解析解

苏雁飞 赵占文 张彬

四边固支复合材料矩形平板轴压失稳的解析解

苏雁飞 赵占文 张彬

(航空工业第一飞机设计研究院，西安 710089)

为了得到四边固支（CCCC）复合材料矩形平板的轴压稳定性计算公式，首先构造了一种满足边界条件的位移函数，应用能量法得到了一种在四边固支边界下复合材料矩形层压板临界失稳载荷计算的解析解。该解析解所得失稳载荷与有限元方法和参考文献的计算结果相差小于5.5%，与试验值结果误差小于5%，位移函数所得波形与有限元结果吻合良好，本文方法可用于四边固支不同长宽比复合材料矩形平板在轴压载荷下的失稳载荷计算。

固支；复合材料；层压板；轴压；稳定性

0 引言

纤维增强复合材料因其优异的疲劳、高比刚度和高比强度特性，在航空航天领域得到了广泛应用。为了提高航空航天飞行器的性能，大量采用薄壁加筋的结构形式，而薄壁结构在外载作用下很容易发生失稳，导致结构承载能力降低，甚至结构失效破坏，因此，复合材料薄壁结构的稳定性问题一直是强度专家学者研究的重点。

对于预测不同边界条件和受载情况下复合材料层压板的临界失稳载荷，除了采用有限元等数值分析方法，解析方法的研究一直占有重要地位。顾诵芬[1]列出了复合材料层压板在四边简支等典型边界条件下受轴压或剪切载荷的失稳载荷计算方法，Shufrin[2]推导了矩形层压板在不同边界条件下求解失稳载荷的半解析解，Qiao[3]采用瑞利-利兹法得到了非加载边弹性约束的复合材料矩形平板受均匀轴压载荷的失稳载荷显式解，Chen[4]计算了弹性约束边界下复合材料矩形平板的剪切临界失稳载荷，袁坚锋[5]研究了复合材料层合板在两边简支两边固支边界下受面内弯曲载荷作用的失稳问题，Lopatin[6]分析了复合材料矩形平板在两边固支两边自由边界下面内弯曲的稳定性。除了解析方法，学者还进行了相关的试验方面研究。万华亮[7]通过试验方法研究了复合材料加筋壁板的失效模式与屈曲稳定性，郭文婧[8]对大尺寸复合材料薄壁加筋结构进行了轴压稳定性试验研究。目前，飞机设计师主要采用复合材料设计参考手册[9,10]给出的半解析半经验公式，通过查询曲线，计算四边固支边界的层压板在均匀压缩载荷下的临界失稳载荷，但该方法只有当屈曲半波数小于3时才适用。通过采用瑞利-利兹法，本文提出了一种在四边固支边界下复合材料矩形层压板临界失稳载荷计算的解析解。

1 模型简化

受到轴压载荷作用的四边固支层压板，其分析模型见图1。图1中为层压板长度；为加载边的宽度；N为单位长度上的均布轴压载荷。定义层压板的长度方向为方向，宽度方向为方向，向符合右手坐标系。

图1 轴压载荷下四边固支矩形板

2 公式推导

将式(2)代入式(5)中，则有

将式(4)和式(6)代入式(7)，可得

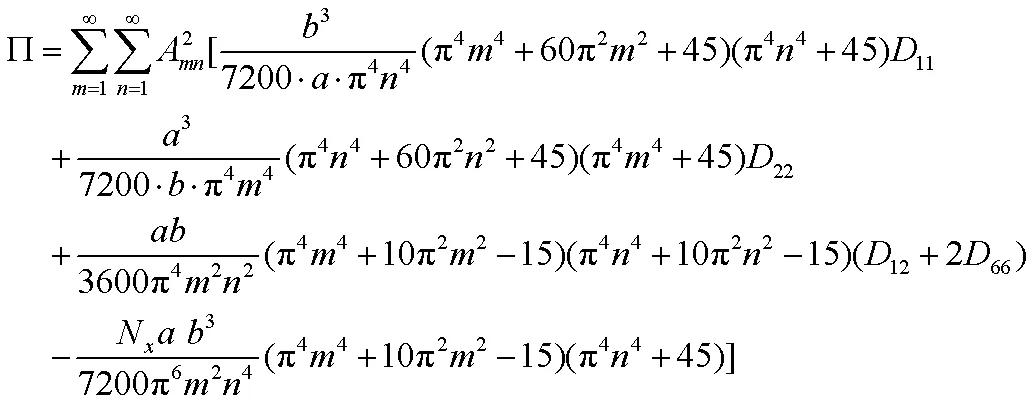
根据最小势能原理，有

将(8)式代入式(9)可得

3 算例分析

3.1 构型设计

某复合材料层压板结构，其所用材料为3238A/CF3031，材料单层厚度为0.23mm，所用材料的性能见表1。设计6种不同构型，层压板构型尺寸见表2。表2中层压板铺层均为[(±45)/ (0/90)/ (±45)2/(0/90)/ (±45)]。

表1 材料特性表

表2 层压板构型表

3.2 结果对比

本文方法、有限元计算与文献[9,10]计算四边固支层压板轴压失稳载荷结果对比见表3。应用MAC.NASTRAN所得各构型的失稳模态图见图2。由图2与表3，应用有限元计算所得波形数与本文所得到的波形数m结果完全一致；且该解析解所得失稳载荷与有限元方法和参考文献的计算结果相差小于5.5%。在=/2时，本文与有限元的面外位移波形对比见图3，可以看出，理论计算的失稳波形与有限元分析结果吻合良好。

表3 计算结果对比表

图2 有限元计算各构型失稳模态图

4 试验研究

一般情况下，设计合理的帽型加筋可以使蒙皮的支持达到固支的状态[11]。为了验证理论计算方法的正确性，设计了复合材料帽形加筋壁板轴向压缩试验。

4.1 试验件构型

试验件考核段长度为500mm，沿轴向布置4根帽形筋条，筋条间距为180mm。试验件两端各延长50mm，端部进行灌胶处理。试验件共计3种构型，每组3件。试验件材料为单向带，材料单层厚度0.14mm，材料性能见表4。3种构型帽形加筋的尺寸均一致，试验件的剖面示意图见图4，帽形筋条剖面示意图见图5，帽形加筋的铺层顺序为[45/02/-45/90/0]s，厚度1.68mm。仅改变蒙皮铺层以及厚度，各构型蒙皮铺层信息见表5。

表4 材料性能表

表5 试验件参数表

图4 试验件剖面尺寸示意图

图5 帽形加筋剖面示意图

4.2 试验件支持与加载

将试验件通过专门的加载夹具安装在材料试验机上进行试验，轴压试验现场见图6。

4.3 试验现象与试验结果

帽形加筋壁板轴压试验的现象为，随着载荷增大，目视观察可见筋条间蒙皮出现较明显的凹凸波纹，试验件出现初始失稳；载荷再增加，筋条发生脱粘，期间不断伴有声响；随着载荷继续增大，筋条脱粘的范围不断扩大，直到筋条发生弯曲破坏或筋条全部脱粘，试验件失去承载能力，试验结束。通过载荷-应变曲线判断初始失稳载荷的大小，试验件正反面贴片，试验失稳点的判断方法为：对称面贴片应变片均值曲线斜率发生拐折的位置，即为试验件发生初始失稳的初始点。每种类型的一件试验件的载荷-应变曲线见图7。

图6 轴压试验现场示意图

每种构型三件试验件的初始失稳载荷平均值定义为该构型试验件的失稳载荷。试验件的失稳载荷见表6。

表6 试验件失稳载荷表

4.4 试验与计算

应用本文方法计算三种构型试验件的失稳载荷与试验值对比结果见表7，其中筋条间距的取值方法见图4。本文中三种构型的试验件取值均为=131mm。由表7，本文所得到的四边固支复合材料矩形平板轴压失稳的解析解与试验结果吻合很好，最大误差不超过5%。

表7 失稳载荷对比表

5 结论

对于在单向轴压载荷下的四边固支复合材料矩形层压板，本文公式计算的失稳波形与有限元模拟结果一致，临界失稳载荷与有限元方法和参考文献的结果最大相差5.5%，与试验值相比最大误差不超过5%，充分证明了本文方法正确可靠，解决了现有工程方法适用范围受屈曲半波数限制的问题，可以满足工程应用的要求。

[1] 顾诵芬. 飞机复合材料结构设计与分析[M]. 上海交通大学出版社, 2011:123.

[2] Shufrin I, Rabinovitch O, Eisenberger M. Buckling of symmetrically laminated rectangular plates with general boundary conditions-A semi analytical approach[J]. Composite Structures, 2008, 82(4):521-531.

[3] Qiao P, Shan L. Explicit local buckling analysis and design of fiber-reinforced plastic composite structural shapes[J]. Composite Structures, 2005, 70(4): 468-483

[4] Chen Q Y, Qiao P Z. Shear buckling of rotationally-restrained composite laminated plates[J]. Thin-walled Structures, 2015, 94:147-154.

[5] 袁坚锋, 尼早, 陈保兴. 面内弯曲载荷作用下两边简支两边固支复合材料层合板的屈曲[J]. 航空学报, 2014, 35(4): 1026-1033. [Yuan Jianfeng, Ni Zao, Chen Baoxing. Buckling of SSCC composite laminates under in-plane bending load[J]. Acta Aeronautica et Astronautica Sinica, 2014,35(4):1026-1033.]

[6] 万华亮, 龚伟明, 覃俊娥. 复合材料帽型加筋壁板轴压稳定性研究[J]. 强度与环境, 2019, 46(1): 31-34. [Wan Hualiang, Gong Weiming, Qin Jun’e. Research on the buckling and post-buckling behavior of hat-stiffened composite panels under axial compressive load[J]. Structure & Environment Engineering, 2019, 46(1): 31-34. ]

[7] 郭文婧, 孙金云, 巴晓蕾, 等. 复合材料薄壁加筋结构轴压稳定性测试分析[J]. 强度与环境, 2020, 47(6):15-21. [Guo Wenjing, Sun Jinyun, Ba Xiaolei, et al. Testing and analysis on the stability of composite structure stiffened with thin wall ribs under axial compression[J]. Structure & Environment Engineering, 2020, 47(6):15-21. ]

[8] Lopatin A V, Morozov E V. Buckling of the CCFF orthotropic rectangular plates under in-plane pure bending [J]. Composite Structure, 2010, 92(6): 1423-1431.

[9] 中国航空研究院. 复合材料结构稳定性分析指南[M]. 北京: 航空工业出版社, 2002: 7-8.

[10] 飞机设计手册总编委会. 飞机设计手册第九册[M]. 北京：航空工业出版社, 2002: 581-582.

[11] 杨俊清, 王俊, 孟庆功. 复合材料帽形加筋壁板轴压屈曲工程算法验证研究[J]. 民用飞机设计与研究, 2019, 1:18-23. [Yang Junqing, Wang Jun, Meng Qinggong. The engineering calculation method of hat-stiffened composite panel under axial compression[J]. Civil Aircraft Design & Research, 2019,1:18-23.]

Buckling Analytic Solution of CCCC Rectangular Composite Laminates under Axial Compression Load

SU Yan-fei ZHAO Zhan-wen ZHANG Bin

(The First Aircraft Institute of the Aviation Industry Corporation of China, Xi’an 710089, China)

In order to obtain the local buckling load of rectangular composite laminates with four sides clamped(CCCC) under axial compression load, a deflection function satisfying the boundary conditions is created, then the critical buckling load is derived using the energy method. It is found that the local buckling load given by analytical solution is not greater than 5.5% compared with the finite element simulation and conference results, and less than 5% compared with test results, and the shape of buckling wave matches well, and . The analytical solution presented can be used for calculate the local buckling load of CCCC rectangular composite laminates with any ratio of length to width under axial compression load.

Clamped, Composite, Laminates, Axial compression, Buckling

V214.3

A

1006-3919(2022)02-0028-06

10.19447/j.cnki.11-1773/v.2022.02.004

2021-05-14；

2021-12-24

航空科学基金(2017ZD03020)

苏雁飞(1983—)，女，高级工程师，研究方向：机身强度设计；（710089）西安市72号信箱303分箱.