锡铅钎料力学性能及本构模型综述

邢睿思 王龙 侯传涛

锡铅钎料力学性能及本构模型综述

邢睿思 王龙 侯传涛

（北京强度环境研究所 可靠性与环境工程技术重点实验室，北京 100076）

锡铅钎料广泛用于航天仪器设备封装结构中，而随着仪器设备向功能多样化和体积小型化发展，仪器设备服役功率更大、温度更高。为了实现封装结构精细化设计，提升仪器设备可靠性与耐久性，需要研究锡铅钎料本构关系，准确模拟其力学行为。本文梳理了锡铅钎料力学性能相关试验研究成果，分析锡铅钎料塑性变形特征。针对宏观唯象本构模型，回顾了国内外相关研究结果，总结了模型特征和适用范围，评价了不同模型对锡铅钎料力学性能的预测效果，为不同载荷环境下本构模型选取提供支撑。

锡铅钎料；力学性能；率相关；本构模型

0 引言

钎料合金广泛用于航天仪器设备封装结构中（如焊点、引脚等结构），主要承担信号联通与机械支撑双重作用，一旦失效可能造成器件甚至系统整体失效，其可靠性成为影响仪器设备可靠性的关键因素之一。近年来，国内外专家学者针对钎料合金机械性能[1]、微观结构[2-4]、本构模型[5]、寿命预测模型[6-10]、仿真分析方法[11]等诸多方面进行回顾与总结，归纳了钎料合金可靠性评价相关问题的发展脉络与研究进展，提出了相关技术理论的优势与不足，为后续发展奠定了基础。Zhang等[1]回顾了合金元素对Sn-Ag无铅钎料机械性能、蠕变行为以及微观结构的影响。Mu等[2]梳理了无铅钎料合金金属间化合物（IMCs）的晶体结构、凝固过程、界面反应及其热机械性能的相关研究成果。MohdSalleh等[3]介绍了Ni含量对无铅钎料IMCs及微观结构的影响，指出在Sn-Cu钎料合金中添加Ni能够改善IMCs层的性能及微观结构，降低热循环下焊点微裂纹出现的可能性。Yao等[5]总结了无铅钎料机械性能试验测试、理论分析和数值仿真相关研究成果。详细介绍了蠕变、单轴拉伸及循环载荷条件下相应的粘塑性本构模型理论框架及发展历程。同时，梳理了封装焊点疲劳寿命预测模型及掉落冲击下的数值仿真分析方法。Lee等[7]归纳了封装焊点疲劳寿命预测模型特点与应用场景，介绍了基于应力、塑性应变、蠕变应变、能量和损伤的寿命预测模型的发展历程。Wong等[9]介绍了蠕变疲劳基本理论，回顾了蠕变疲劳分析方法在电子封装领域的应用。综上，相关的综述类文献从材料和结构的角度出发较为全面的总结了钎料合金可靠性评定工作，对材料性能与可靠性评定方法进行了较为充分的讨论，然而在钎料本构模型方面仅仅介绍了相关理论的基本框架，缺乏对比分析，没有形成本构模型预测能力的评价方法。因此，本文详细梳理了钎料合金粘塑性本构模型的发展历程，分析模型的特点并评价不同本构模型的预测能力，最终针对锡铅钎料给出不同本构模型相应的适用范围。

1 本构模型

航天仪器设备在服役过程中既会面临较大的振动、冲击等机械载荷，也会面临较长贮存条件下的温度循环及大电流等热、电载荷。封装结构处于复杂、严苛的服役环境下，对于一般金属材料，当环境温度超过0.3倍金属熔点温度时（Tm），蠕变对于材料的影响已经不可忽视。钎料合金普遍熔点较低（如63Sn37Pb熔点为456K），在室温环境下会发生明显的蠕变变形。考虑到钎料合金在变形过程中，塑性变形与蠕变同时产生、相互影响的特性且二者的位错运动机制是统一的，采用统一的具有单一内变量的本构模型更符合物理意义，因此统一粘塑性本构模型得到广泛应用。

1.1 MATMOD模型

早在1976年Miller[12]提出了一个统一粘塑性本构模型用以描述金属材料非弹性变形过程中的蠕变行为以及短时塑性现象，并将其命名为MATMOD模型。模型的粘度函数为双曲正弦函数与幂函数组合的形式，使用单一背应力描述随动强化，拖拽应力描述各向同性强化。同时，背应力与拖拽应力均为率相关函数且含有恢复项用以描述初始强化的非线性特征。模型流动率方程如式（1）所示

其中，为背应力，为拖拽应力。’为温度相关项，其函数表达式为

其中，为理想气体常数，m为金属熔点，、为材料参数。当≥0.6m时，激活能为定值；当<0.6m时,激活能随温度降低而下降。内变量演化方程如式（3）

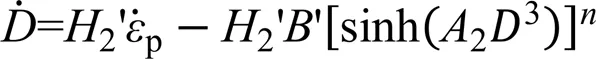
MATMOD模型能够预测材料短时塑性变形、长时蠕变变形、循环变形以及静态恢复和动态会议效应。然而模型中各向同性强化率和随动强化率方程相互影响且形式复杂，不利于理解以及模型参数确定。基于此，Miller等[13-14]提出了简化的MATMOD模型以解决上述问题，同时为了进一步提高模型对于固溶强化材料如锆合金、铝合金以及奥氏体不锈钢的预测精度，改进的MATMOD模型在各向同性强化率中引入固溶强化项扩展模型适用范围。在随后的发展过程中，包括应变软化等瞬态现象，温度、应变率、加载方向改变时载荷历史效应等影响因素，相继被引入到MATMOD模型中扩展模型的预测范围[15-16]。

1.2 Bodner-Partom模型

1.3 Anand模型

Anand本构模型[24]广泛地应用在电子封装领域，将形变阻抗与位错密度、固溶体强化及晶粒尺寸等微观参量进行关联，用以描述材料应力-应变关系。由于Anand本构模型数学形式简单，模型参数少，且易于确定，因此被嵌入到ANSYS与ABAQUS等有限元软件中并广泛地应用在电子封装焊点的力学分析与寿命预测中[25-28]。同时，大量的研究学者针对Anand模型不足，考虑环境温度影响[29]、动态再结晶[30]、加工硬化或软化规律[31]以及辐照影响[32]等不同影响因素，建立了众多修正的本构模型提升模型预测精度，扩展模型适用范围

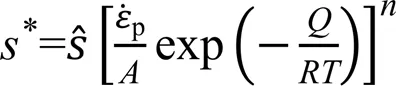
1.4 VBO模型

Krempl和Cernocky认为非弹性应变率由过应力决定，根据不锈钢及钛合金单轴拉伸试验结果，以幂函数的形式定义了流动率，发展了基于过应力的粘塑性理论（VBO模型）[33-36]。模型总应变率由弹性应变率和塑性应变率两部分组成

1.5 Garofalo-Arrhenius模型

典型的蠕变试验可以分为三个阶段：初始蠕变阶段、稳态蠕变阶段和加速蠕变阶段，其中稳态蠕变阶段持续时间最长，如何刻画不同温度和加载条件下材料稳态蠕变率也成为国内外学者的关注重点。Garofalo-Arrhenius模型采用双曲正弦函数描述材料稳态蠕变应变率，并用于封装焊点仿真分析与寿命预测中[38-41]，模型基本形式为

其中，1和2为温度相关参数具体形式为

1.6 Wiese模型

Wiese等开展了无铅钎料蠕变变形试验研究并提出了Wiese本构模型用描述材料稳态蠕变应变率。稳态蠕变应变率由两部分组成，分别用来描述低应力和高应力作用下焊点蠕变速率。由于Wise形式简单，易于嵌入有限元程序，被广泛用于分析封装焊点可靠性及疲劳寿命[42,43]。

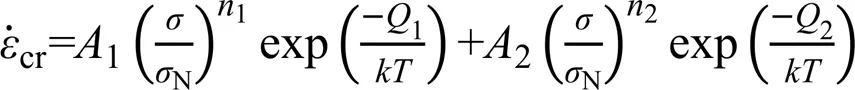
1.7 Norton模型

Norton蠕变方程作为最简单的稳态蠕变模型之一被广泛应用于金属材料本构方程流动率中，模型形式简单、参数获取难度低，因此在钎料合金中应用较为常见[44-45]。

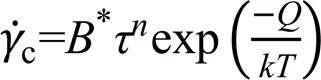
1.8 Johnson-Cook模型

Johnson和Cook[46]基于不同应变率下扭转试验、霍普金森杆试验和准静态拉伸试验结果，提出了Johnson-Cook粘塑性本构模型，模型应力表达式由应变强化项、率相关项和温度相关项三部分构成，模型表达式清晰、物理意义明确且参数获得容易被广泛用于预测金属材料动态载荷下的变形。然而模型不能准确描述宽泛应变率和较大温度范围内材料的本构关系，针对模型不足，Maheshwari等[47]修正了应变率相关项和温度相关项提升了模型的预测精度。Wang等[48]考虑温度对应变强化和应变率强化的影响，建立了修正的J-C本构模型。近年来，针对钎料合金[49,50]、铝合金[51]以及高熵合金[52]等材料动态载荷下力学响应的不同特征，建立了相应的修正的J-C本构模型，进一步提升模型预测能力

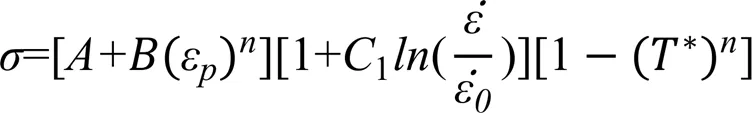
其中，m为材料熔点温度，r为参考温度一般取室温。

1.9 Zerilli-Armstrong模型

Zerilli和Armstrong[53]继J-C模型之后提出了Z-A本构方程用以描述材料动态载荷下的塑性变形。模型综合考虑应变硬化影响、应变率硬化影响、温度影响以及晶体结构影响。模型基本形式如下

2 分析与讨论

2.1 锡铅钎料力学性能分析

由于应用环境的相似性，锡铅钎料力学性能具有相似性。如图1所示，313K、0.02s-1应变率条件下，63Sn37Pb、60Sn40Pb、40Sn60Pb和10Sn90Pb饱和应力相差不超过10MPa；398K、0.02s-1应变率条件下，63Sn37Pb、60Sn40Pb、40Sn60Pb和10Sn90Pb饱和应力相差不超过5MPa，（数据引自文献[57]）。

图1 锡铅钎料单轴拉伸试验应力-应变曲线

因此，本文以63Sn37Pb锡铅钎料为例分析锡铅钎料力学性能并为后续本构模型特性分析提供数据支撑。

63Sn37Pb锡铅钎料室温环境下不同应变率下(3×10-5～1800 s-1)动态拉伸试验和准静态拉伸试验结果[58-60]如图2所示。材料呈现典型的率相关特征，随着应变率的增加材料整体应力水平不断提高。当应变率低于0.2s-1时，随着应变增加，应力在经过初始阶段快速增加后保持恒定；当应变率介于0.2与200s-1之间时，随着应变增加，应力在初始阶段快速增加后进入线性增加阶段，应力增加速率保持恒定；而当应变率进一步提高至1800s-1时，应力增加在不同阶段皆呈现非线性特征。可知，材料在低应变率条件下存在应力饱和值而高应变率条件下应力持续增加不存在饱和值。

不同温度下63Sn37Pb锡铅钎料拉伸试验结果如图3所示，材料在不同温度下应力-应变曲线与室温下呈现相同特征。此外，当应变率保持恒定时，材料应力水平随温度上升不断下降。为了进一步分析材料率相关及温度相关特征，取不同试验条件下5%应变对应应力值，将其定义为饱和应力，绘制塑性应变率-饱和应力与温度-饱和应力曲线，结果分别如图3和图4所示，相关特征将在后续章节中结合不同本构模型详细讨论。本文所使用63Sn37Pb试验数据部分引自文献，其中应变率范围在1200～1800 s-1内的试验数据引自文献[58]；应变率范围在2×10-3～200 s-1内的试验数据引自文献[59-60]；应变率范围在3×10-5～2×10-3s-1内的试验数据通过锡铅钎料单轴拉伸试验获取。

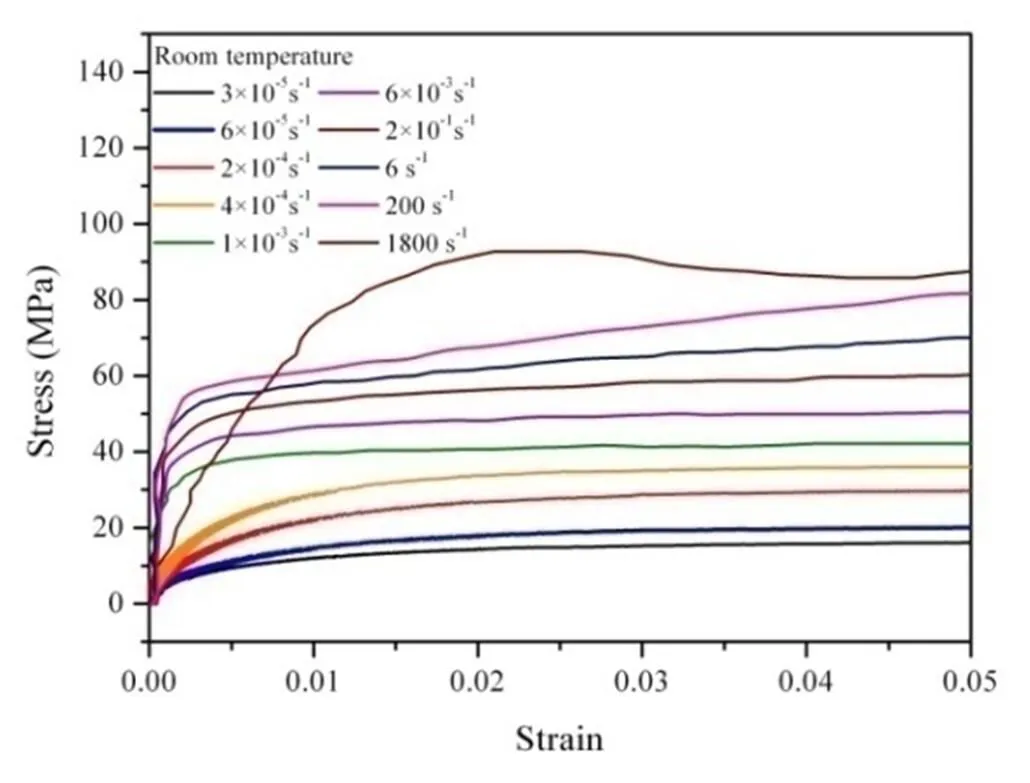
图2 室温环境下63Sn37Pb锡铅钎料单轴拉伸试验应力-应变曲线

图3 不同温度环境下63Sn37Pb锡铅钎料单轴拉伸试验应力-应变曲线[59]

2.2 本构模型率相关特征分析

室温环境下饱和应力随塑性应变率演化过程试验结果与模型预测结果如图4所示。在双对数坐标下，63Sn37Pb锡铅钎料饱和应力-塑性应变率曲线，在低应变率段（小于0.2 s-1）呈现高度非线性特征，在高应变率段（大于0.2 s-1）非线性特征并不明显反而更接近线性特征。Miller模型流动率方程为双曲正弦函数与幂函数组合的形式，既能够较好的预测低应变率阶段材料饱和应力的非线性增长，又能较好预测的高应变率段饱和应力近似线性增长的特征。此外，随着塑性应变率增加Miller模型呈现明显的饱和效应即随着塑性应变率的增加，饱和应力增加十分有限。整体而言，Miller模型能够较好的描述锡铅钎料饱和应力和塑性应变率间的关系，在所有模型中预测效果最好。

B-P模型流动率方程采用指数函数与幂函数组合的形式，在低应变率段接近线性增长，而在高应变率段呈现明显的非线性增长特征且随着塑性应变率增加饱和应力增长速度越来越快，不具有饱和效应。B-P模型仅能较好预测应变率介于1×10-4与1×10-2s-1之间材料的饱和应力，整体预测效果不佳，可见B-P模型并不适用于较大应变率范围内锡铅钎料率相关性能的预测。

J-C模型流动率方程为指数函数形式，Kock模型在此基础上引入粘度指数，两者在形式上较为接近，同时模拟曲线也极为接近，且均呈现明显的饱和效应。在低应变率段模型过高的估计了材料饱和应力值，而在高应变率段模型能够较好的预测材料饱和应力值。

Anand模型和Garofalo模型的流动率方程与Miller模型相似，均为指数函数与幂函数组合的形式，然而相比于Miller模型Anand和Garofalo模型饱和效应相对不明显。模型在低应变率段预测结果同样较为准确，而在高应变率预测偏差较大。

Dorn模型流动率方程为幂函数形式，且不具有饱和效应，仅能较好预测应变率介于1×10-4与1×10-2s-1之间材料的饱和应力。Wiese模型两项均为幂函数形式，可以看作两个Dorn模型的叠加，模型在低应变率段预测效果较好而在高应变率预测偏差极大且不具有饱和效应。

Z-A模型流动率函数为指数函数与对数函数组合的形式，模型在全应变率段线性增加，整体预测偏差较大。

SVBO模型同样为幂函数形式类似，且在全应变率段线性增加，整体预测偏差较大。VBO模型则呈现，明显的饱和效应模型在高应变率段能够较好的预测材料饱和应力，而当应变率低于1×10-4模型预测偏差较大。

综上，在低应变率段，Miller、Anand、Garofalo和Wiese模型能够较好的预测63Sn37Pb锡铅钎料饱和应力-塑性应变率曲线；在高应变率段，Miller、J-C、Kocks和VBO模型预测结果较好。然而必须指出模型参数是根据室温环境下低应变率段试验结果确定的，不能轻易断定在高应变率段预测结果欠佳的模型就不一定适于高应变率段锡铅钎料饱和应力的预测，在实际选取模型时还要根据具体使用场景判定应变率范围重新确定参数。

2.3 本构模型温度相关特征分析

环境温度作为影响钎料合金力学性能的重要因素，同样是统一粘塑性本构模型需要重点考虑的对象。一般情况下，描述温度影响的方法可以分为两种：其一是在原有方程基础上外乘温度修正项，如Dorn模型在流动率方程上外乘Arrhenius项；其二是构建关键材料参数与环境温度的函数，如B-P模型中材料参数。本文选取Miller、B-P等9个本构模型分析温度相关特征，模型流动率方程及模型参数如表2所示。

塑性流动率为1×10-3s-1时，饱和应力随温度演化过程试验与模型预测结果如图5所示，在双对数坐标下，饱和应力随温度的降低而不断增加且增加速率不断下降，与应变率饱和效应相似，饱和应力随温度降低同样呈现饱和趋势，本文称其为低温饱和效应。

图4 塑性应变-饱和应力试验与本构模型预测结果

图5 温度-饱和应力试验与本构模型预测结果

进一步分析温度对模型率相关特征的影响，选取环境温度在228K～423K之间，应变率在1×10-5～1×10-2s-1之间数据进行分析，不同温度下饱和应力随塑性应变率变化试验结果与模型拟合曲线如图6所示，63Sn37Pb锡铅钎料应变率敏感度随温度的降低而不断下降，即随着温度降低，饱和应力随应变率增加的增加幅度越来越小。如图6a) 所示，Miller模型拟合曲线随温度降低而逐渐变得平缓，即相同应变率下曲线斜率不断减小。

表2 不同本构模型流动率方程与模型参数

模型能够较好的描述锡铅钎料应变率敏感度随温度的变化情况。B-P模型与J-C模型拟合曲线分别如图6b) 和c) 所示，不同温度拟合曲线近似相互平行，模型并不能很好刻画温度对锡铅钎料应变率敏感度的影响且整体预测偏差较大。Anand模型、G-A模型与Wiese模型预测结果如图6 d)、e)、f)所示，模型均能较好的描述锡铅钎料应变率敏感度随温度的变化情况，其中Anand模型对低温环境下试验结果的预测精度略低而其他环境温度下预测精度较高。Wiese模型与对低温环境下试验结果预测偏差较大而其他环境温度下预测精度较高。G-A模型能够较好的预测低温环境下饱和应力随塑性应变率变化曲线而高温环境下预测偏差较大。Dorn模型与Z-A模型预测结果与B-P模型类似如图6g)、h)所示，模型同样不能刻画温度对锡铅钎料应变率敏感度的影响且预测精度较低。

图6 塑性应变率-饱和应力试验与本构模型预测结果

2.4 本构模型应变强化特征分析

根据前文所介绍的不同统一粘塑性本构模型具体特征，可将模型分为三类：第一类本构模型以G-A、Wiese和Dorn模型为代表，模型仅能描述蠕变试验中稳态蠕变应变率与应力间的关系，因此只能描述单轴拉伸曲线中饱和应力值与塑性应变率间的关系，不能描述应变强化效应，即不能刻画单轴拉伸应力-应变曲线中初始强化段；第二类本构模型以Miller、B-P和Anand模型为代表，模型考虑了温度相关、率相关以及应变强化等影响因素且在恒定应变率下应力增长存在饱和值与锡铅钎料在低应变率段力学性能一致；第三类本构模型以J-C和Z-A模型为代表，模型考虑了温度相关、率相关以及应变强化等影响因素且在恒定应变率下应力增长不存在饱和值与锡铅钎料在高应变率段力学性能一致。综上可知，第二类和第三类能够描述材料应变强化特征，而第二类本构模型更适于锡铅钎料在低应变率段力学性能预测而第三类锡铅钎料在高应变率段力学性能预测。根据前文分析结果可知，在第二类本构模型中Miller模型和Anand模型能够较好的描述材料在低应变率段率相关与温度相关特征，因此选取其作为进一步分析对象。同时，选取J-C与Z-A模型作为研究对象，根据锡铅钎料在高应变率段试验结果重新确定模型材料参数，进一步分析模型预测能力。忽略各向同性强化和环境温度影响以简化模型参数聚焦应变强化特征，Miller模型简化后应力表达式为

Anand模型表达式如式(11)-(13)所示，去除其中Arrhenius项即为不考虑温度影响的Anand本构模型。J-C与Z-A模型分别为

模型参数如表3所示。

表3 不同本构模型参数

锡铅钎料单轴拉伸试验及本构模型预测结果如图所示，Anand模型能够较好的模拟材料初始强化阶段非线性特征，而Miller模型在初始强化阶段拟合曲线近似线性增长不能很好的描述材料力学性能，可见Anand本构模型更适于描述锡铅钎料在低应变率段的力学性能。

高应变率段本构模型拟合曲线如图8所示，J-C和Z-A模型均能模拟材料应变强化特征，其中J-C模型拟合曲线稳定增长阶段斜率随应变率提高而不断增加，而Z-A模型不同应变率下拟合曲线近似平行，结合文献中试验结果如图3所示，可知J-C模型与锡铅钎料在高应变率段力学性能更为吻合。

图7 单轴拉伸试验与本构模型预测结果

图8 J-C与Z-A本构模型应力-应变拟合曲线

3 结论

本文结合国内外相关研究成果以63Sn37Pb为例分析了锡铅钎料塑性变形特征，梳理了钎料合金统一粘塑性本构模型的发展历程，总结并分析不同本构模型率相关、温度相关以及应变强化特征，得出以下结论：1）锡铅钎料呈现典型的率相关、温度相关和应变强化特征。材料在低应变段材料存在饱和应力值。饱和应力随应变增加呈现非线性增长，且饱和应力变化存在应变率饱和效应；饱和应力随温度降低不断增加且呈现低温饱和效应。2）Miller、Anand、G-A和Wiese本构模型应变率饱和效应不明显，但能够较好的描述材料在低应变率段率相关特征；Miller、J-C、Kocks和VBO本构模型呈现明显应变率饱和效应，能够较好的描述材料在高应变率段率相关特征。3）Miller、Anand和G-A模型能够较好的描述材料低温饱和效应，B-P、Wiese、Dorn和Z-A不能描述材料低温饱和效应。Miller、Anand、G-A和Wiese模型能够较好的描述温度对材料应变率敏感度的影响，其他模型则不能很好的反映材料应变率敏感度随温度变化情况。4）Anand模型预测结果更接近锡铅钎料低应变率段应变强化特征，而J-C模型预测结果更接近锡铅钎料高应变率段应变强化特征。

综上，本文以63Sn37Pb锡铅钎料为例，分析了不同本构模型的特征与预测能力，为不同载荷环境下本构模型选取提供支撑，对航天仪器设备封装结构精细化设计提供基础。

[1] Liang Z, He C W, Guo Y H, et al. Development of Sn Ag-based lead free solders in electronics packaging-ScienceDirect[J]. Microelectronics Reliability, 2012, 52(3): 559-578.

[2] Mu D K, Mcdonald S D, Read J, et al. Critical properties of Cu6Sn5 in electronic devices: Recent progress and a review[J]. Current Opinion in Solid State & Materials Science, 2016, 20(2):55-76.

[3] Salleh M AA M, Sandu I G, Abdullah M M A, et al. Nickel (Ni) Microalloying Additions in Sn-Cu Lead-free Solder. Short Review[J]. IOP Conference Series: Materials Science and Engineering, 2017, 209:012084.

[4] Anderson I E, Choquette S, Reeve K T, et al. Pb-free solders and other joining materials for potential replacement of high-Pb hierarchical solders[C]. IEEE, 2018:1-11.

[5] Yao Y, Long X, Keer L M. A review of recent research on the mechanical behavior of lead-free solders[J]. Applied Mechanics Reviews, 2017, 69(4):040802.

[6] Winslow J W, Silveira C D. A Brief. Selective review of thermal cycling fatigue in eutectic tin-lead solder[J]. 1993.

[7] Lee W W, Nguyen L T, Selvaduray G S. Solder joint fatigue models: review and applicability to chip scale packages[J]. Microelectronics Reliability, 2000, 40(2):231-244.

[8] Tonapi S, Gopakumar S, Borgesen P, et al. Reliability of lead-free solder interconnects-a review[C]. IEEE, 2002.

[9] Wong E H, Van Driel W D, Dasgupta A, et al. Creep fatigue models of solder joints: A critical review[J]. Microelectronics Reliability, 2016, 59:1-12.

[10] Fang L, Bo J, Wei T. Review of board-level solder joint reliability under environmental stress[C]. 2016 Prognostics and System Health Management Conference (PHM-Chengdu). IEEE, 2016.

[11] Massiot G, Munier C. A review of creep fatigue failure models in solder material-simplified use of a continuous damage mechanical approach[C]. International Conference on Thermal & Mechanical Simulation & Experiments in Microelectronics & Microsystems. IEEE, 2004.

[12] Miller A K. An inelastic constitutive model for monotonic, cyclic, and creep deformation: Part I-equations development and analytical procedures[J]. Trans. ASME, Journal of Engineering Materials and Technology, 1976, 98(2):97.

[13] Miller A K, Sherby O D. A simplified phenomenological model for non-elastic deformation: Predictions of pure aluminum behavior and incorporation of solute strengthening effects[J]. Acta Metallurgica, 1978, 26(2):289-304.

[14] Schmidt C G, Miller A K. A unified phenomenological model for non-elastic deformation of type 316 stainless steel, Part II: Fitting and predictive capabilities. 1981.

[15] Lowe T C. Procedures for determining MATMOD-4V material constants[M]. 1993.

[16] Henshall G A, Helling D E, Miller A K. Improvements in the MATMOD equations for modeling solute effects and yield-surface distortion[J]. Unified Constitutive Laws of Plastic Deformation, 1996:153-227.

[17] Bonder S R. Constitutive equations for elastic-viscoplastic strain-hardening materials[J]. Trans. ASME, Journal of Applied Mechanics, 1975.

[18] Bodner S R.Evolution equations for anisotropic hardening and damage of elastic-viscoplastic materials[J]. 1985.

[19] Moreno V, Jordan E H. Prediction of material thermomechanical response with a unified viscoplastic constitutive model[J]. International Journal of Plasticity, 1986, 2(3):223-245.

[20] Fz A, Na A, Kw B, et al. Constitutive equations for the viscoplastic-damage behaviour of a rubber-modified polymer[J]. European Journal of Mechanics - A/Solids, 2005, 24(1):169-182.

[21] Skipor A F, Harren S V, Botsis J. On the constitutive response of 63/37 Sn/Pb eutectic solder[J]. Journal of Engineering Materials and Technology, 1996, 118(1):1-11.

[22] Chabaud B M, Brock J S, Williams T O. Benchmark analytic solution of the dynamic sphere problem for Bodner–Partom elastic-visco plastic materials[J]. European Journal of Mechanics- A/Solids, 2015, 49(1):114-124.

[23] Klosowski P, Zerdzicki K, Woznica K. Identification of Bodner-Partom model parameters for technical fabrics[J]. Computers & Structures, 2017, 187(JUL.):114-121.

[24] Anand L. Constitutive equations for hot-working of metals[J]. International Journal of Plasticity, 1985, 1(3):213-231.

[25] Wilde J, Becker K, Thoben M, et al. Rate dependent constitutive relations based on Anand model for 92.5Pb5Sn2.5Ag solder[J]. IEEE Transactions on Advanced Packaging, 2002, 23(3):408-414.

[26] Yu D J, Xu C, Gang C, et al. Applying Anand model to low-temperature sintered nanoscale silver paste chip attachment[J]. Materials and Design, 2009, 30(10):4574-4579.

[27] 童军, 侯传涛, 荣克林. 温循载荷作用下电路板焊点的疲劳寿命评估[J]. 强度与环境, 2014, 41(4):48-52. [Tong J, Hou C T, Rong K L. Life evaluation of solder joints of circuit boards under thermally cyclic loading[J]. Strength and environment, 2014, 41(4):48-52.]

[28] 景博, 李龙腾, 胡家兴. 耦合环境应力下电子设备焊点退化试验研究[J]. 强度与环境, 2020, 47(1):55-63. [Jing B, Li L T, Hu J X. Degradation experiment study on solder joint of electronic equipment under coupling stress[J]. Strength and Environment, 2020, 47(1):55-63.]

[29] Xu C, Gang C, Sakane M. Prediction of stress-strain relationship with an improved and constitutive model for lead-free solder Sn-3.5Ag[J]. IEEE Transactions on Components & Packaging Technologies, 2005, 28(1):111-116.

[30] Bianchi J H, Karjalainen L P. Modelling of dynamic and metal dynamic recry stallisation during bar rolling of a medium carbon spring steel[J]. Journal of Materials Processing Technology, 2005, 160(3):267-277.

[31] Puchi-Cabrera E S, JD Guérin, Barbera-Sosa J L, et al . Plausible extension of Anand's model to metals exhibiting dynamic recrystallization and its experimental validation[J]. International Journal of Plasticity, 2018: S0749641917306411.

[32] Wang Y Y, Zhao J J, Zhang C. Viscoplastic equations incorporated into a finite element model to predict deformation behavior of irradiated reduced activation ferritic/martensitic steel[J]. Fusion Engineering and Design, 2017, 118:129-134.

[33] Cernocky E P, Krempl E. A non-linear uniaxial integral constitutive equation incorporating rate effects, creep and relaxation[J]. International Journal of Non-Linear Mechanics, 1979, 14(3):183-203.

[34] Cernocky E P, Krempl E. A theory of viscoplasticity based on infinitesimal total strain[J]. Acta Mechanica, 1980, 36(3-4):263-289.

[35] Krempl E, Mcmahon J J, Yao D. Viscoplasticity based on overstress with a differential growth law for the equilibrium stress[J]. Mechanics of Materials, 1986, 5(1):35-48.

[36] Krempl H E. Extension of the viscoplasticity theory based on overstress (VBO) to capture non-standard rate dependence in solids[J]. International Journal of Plasticity, 2002.

[37] Maciucescu L, Sham T L, Krempl E. Modeling the deformation behavior of a Sn-Pb solder alloy using the simplified viscoplasticity theory based on overstress (VBO)[J]. Asme Journal of Electronic Packaging, 1999, 121(2):92-98.

[38] Darveaux R, Banerji K. Constitutive relations for tin-based solder joints[J]. IEEE Transactions on Components Hybrids & Manufacturing Technology, 1992, 15(6):1013-1024.

[39] Lau J H, Lee S. Modeling and analysis of 96.5Sn-3.5Ag lead-free solder joints of wafer level chip scale package on buildup microvia printed circuit board[J]. Electronics Packaging Manufacturing IEEE Transactions on, 2002, 25(1):51-58.

[40] Tseng S C, Chen R S, Lio C C. Stress analysis of lead-free solders with under bump metallurgy in a wafer level chip scale package[J]. International Journal of Advanced Manufacturing Technology, 2006, 31(1-2):1-9.

[41] Amalu E H, Ekere N N. Modelling evaluation of Garofalo-Arrhenius creep relation forlead-free solder joints in surface mount electronic componentassemblies[J]. Journal of Manufacturing Systems, 2016, 39:9-23.

[42] Wiese S, Roellig M, Wolter K J. Creep of thermally aged SnAgCu-solder joints[J]. IEEE, 2005.

[43] Stoeckl S, Yeo A, Lee C, et al. Impact of fatigue modeling on 2ndlevel joint reliability of BGA packages with SnAgCu solder balls[C]. Electronic Packaging Technology Conference. IEEE, 2005, 2:857-862.

[44] Lee S R, Zhang X. Sensitivity study on material properties for the fatigue life prediction of solder joints under cyclic thermal loading[J]. Circuit World, 1998, 24(3):26-31.

[45] Lau J H, Lee S W, Pan S H, et al. Nonlinear time dependent analysis of Micro via-in-pad substrates for solder bumped flip chip applications[J]. Journal of Electronic Packaging, 2002, 124(3):205211

[46] Cook J. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressure[J]. Engineering Fracture Mechanics, 1985, 21(1): 31-48.

[47] Maheshwari A K, Pathak K K, Ramakrishnan N, et al. Modified Johnson-Cook material flow model for hot deformation processing[J]. Journal of Materials Science, 2010, 45(4): 859-864.

[48] Wang B, Liu Z, Song Q, et al. A modified Johnson-Cook model and its application to high-speed machining of 7075-T7451 aluminum alloy[J]. Journal of Manufacturing Science and Engineering, 2019, 141: 1-15.

[49] 秦飞, 安彤, 王旭明. 考虑损伤效应的无铅焊锡材料的率相关本构模型[J]. 北京工业大学学报, 2013, 39(1):5. [Qin F, An T, Wang X M. Rate-dependent constitutive model for lead-free solders considering damage effect[J]. Journal of Beijing University of Technology, 2013, 39(1):5. ]

[50] Vafaeenezhad H, Seyedein S H, Aboutalebi M R, et al. Incorporating the johnson-cook constitutive model and a soft computational approach for predicting the high-temperature flow behavior of Sn-5Sb solder alloy: a comparative study for processing map development[J]. Journal of Electronic Materials, 2017, 46:467-477.

[51] Zhang Y B, Song Y, Hong X, et al. A modified Johnson-Cook model for 7N01 aluminum alloy under dynamic condition[J]. Journal of Central South University, 2017, 24(011):2550-2555.

[52] Bobbili R, Madhu V. A modified Johnson-Cook model for FeCoNiCr high entropy alloy over a wide range of strain rates[J]. Materials Letters, 2018, 218:103-105.

[53] Zerilli F J, Armstrong R W. Dislocation‐mechanics‐based constitutive relations for material dynamics calculations[J]. Journal of Applied Physics, 1987, 61(5): 1816-1825.

[54] Abed F H, Voyiadjis G Z. A consistent modified Zerilli-Armstrong flow stress model for BCC and FCC metals for elevated temperature[J]. Acta Mechanica, 2005, 175(1-4):1-18.

[55] Jiang L, Li F, Cai J, et al. Comparative investigation on the modified Zerilli–Armstrong model and Arrhenius-type model to predict the elevated-temperature flow behavior of 7050 aluminum alloy[J]. Computational Materials Science, 2013, 71(3):56-65.

[56] Zhang H, Wang G, Kent D, et al. Constitutive modeling of the flow behavior of a β titanium alloy at high strain rates and elevated temperatures using the Johnson-Cook and modified Zerilli-Armstrong models[J]. Materials Science & Engineering A, 2014, 6(12):71-79.

[57] 张莉. 焊锡钎料温度与应变率相关拉伸性能的本构描述[D].天津大学, 2014.[Zhang L. Constitutive description of temperature and strain rate dependent tensile behaviors of solder[D]. Tianjin University, 2014.]

[58] 秦飞, 安彤. 焊锡材料的应变率效应及其材料模型[J]. 力学学报, 2010, 42(3):9. [Qin F, An T. Strain rate effects and material models of solders[J]. Chinese Journal of Theoretical and Applied Mechanics, 2010, 42(3):9.]

[59] Pang H, Wang Y P, Shi X Q, et al. Sensitivity study of temperature and strain rate dependent properties on solder joint fatigue life[C].Electronics Packaging Technology Conference. IEEE, 1998.

[60] Boyce, Lee B, Neilsen, et al. On the strain rate and temperature-dependent tensile behavior of Eutectic Sn-Pb Solder[J]. Journal of Electronic Packaging, 2010, 133:031009-1.

Review of Mechanical Properties and Constitutive Model of Tin-Lead Solder

XING Rui-si WANG Long HOU Chuan-tao

（Science and Technology on Reliability and Environmental Engineering Laboratory,Beijing Institute of Structure and Environment Engineering,Beijing 100076,China）

Tin-lead solders have been widely used in the package structure of aerospace instruments. With the miniaturization of volume and functional diversification of aerospace instruments, the instruments service in higher temperature and power. In order to satisfy the precise design requirements and improve the reliability and durability of the package structures, the constitutive model of tin-lead solders should be investigated. In this paper, a review was presented on the mechanical properties and macro phenomenal constitutive models of tin-lead solders. Different constitutive models were summarized and discussed in details, which was beneficial for model selection.

Tin-lead solders; Mechanical properties; Rate dependent; Constitutive model

V417+.4

A

1006-3919(2022)02-0015-13

10.19447/j.cnki.11-1773/v.2022.02.003

2021-07-15；

2021-10-22

科技部国家重点研发计划（2021YFB3801700）;重点实验室基金（6142911180512）

邢睿思（1991—），男，博士，工程师，研究方向：结构完整性，（100076）北京9200信箱72分箱.