曲线纤维复合材料后掠机翼的颤振特性优化

杨执钧 于洋 高博 郭静

曲线纤维复合材料后掠机翼的颤振特性优化

杨执钧1于洋2高博1郭静1

（1北京强度环境研究所可靠性与环境工程技术重点实验室，北京，100076; 2北京强度环境研究所，北京，100076）

曲线纤维铺层是制造变刚度复合材料层合板的一种新技术，本文以12层曲线纤维复合材料后掠机翼为研究对象，研究了不可压缩流动中后掠机翼的颤振特性优化，分析了纤维方向、优化层数和铺层厚度对颤振特性的影响。数值仿真中分别采用有限元法和高阶面元法建立后掠机翼的结构模型和气动力模型，利用VG法求解后掠机翼的颤振边界。计算结果表明，后掠机翼全部铺层采用曲线纤维时优化后颤振速度，比仅最外层采用时提高31.1%，比全部铺层采用直线纤维时优化后颤振速度提高14.3%。铺层全部采用二维方向可变曲线纤维时的颤振速度比一维角度可变的颤振速度仅提高1.7%，证明纤维方向沿展向可变对颤振边界影响更大。纤维方向和厚度共同优化时，在不改变后掠机翼总厚度的情况下可使后掠机翼的颤振速度再次提高5.4%。研究表明，采用曲线纤维进一步提高了复合材料层合板的可设计性，通过调整曲线纤维路径可以明显改变复合材料后掠机翼的颤振特性。

颤振特性优化；曲线纤维；变刚度复合材料；高阶面元法

0 引言

气动弹性优化是气动弹性领域的一个分支，其目的是通过对结构和气动共同优化，以被动的方式提高飞行器性能。气动弹性优化目标主要包括提高颤振速度[1-2]，减重[3]，减阻[4]，阵风响应减缓[5-6]，最佳颤振特性[7]以及组合目标[8-10]。为了达到以上目标，气动弹性优化通常涉及修改机翼的刚度和机翼弯曲、扭转变形之间弹性耦合。已有大量学者研究采用复合材料层合板设计的机翼结构[11-12]，通过对纤维方向和分层序列进行调整，充分利用复合材料结构的弯扭耦合效应，设计出满足结构刚度、强度以及气动弹性等性能指标要求且使得结构重量更轻的飞行器结构。因此，自上世纪80年代以来，复合材料机翼的气动弹性优化研究取得了重大进展。

新型飞行器的探索，包括大长细比弹性机翼、翼身融合飞行器以及变形机翼，依赖于多学科的设计优化方法，其中先进的复合材料结构气动弹性优化可能是关键的技术。然而传统的纤维增强复合材料层合板采用的是直线纤维，也就是说纤维方向在单层内是不变的，导致气动弹性优化的可设计空间受限，无法发挥复合材料层合板的全部优势。在过去的20年内发展的复合材料曲线纤维技术，可以令复合材料单层纤维按照不断变化的“局部零点”排列，即纤维是沿着机翼内部实际载荷情况的路径弯曲排列而成。这种含曲线纤维铺层的复合材料称为变刚度复合材料。变刚度符合材料中的纤维层可与载荷精准对齐，将有助于生产出具有更高展弦比、更轻质坚固且阻力更低的机翼。

Gurdal等[13-14]首先提出了变刚度复合材料的概念，通过分析和实验证明曲线纤维复合材料层合板与直线纤维复合材料相比，其屈曲强度和后屈曲性能有较大提高。Lopes等[15]研究结果表明曲线纤维的不连续性能够降低几何间断导致的应力集中。Honda和Narita[16]将曲线纤维应用于变形机翼的研究中。杜宇等[17]采用有限元法研究了变刚度复合材料的失效性能。随后学者们研究了变刚度复合材料层合板在气动弹性裁剪中的应用。Haddadpour和Zamani[18]采用薄壁梁机翼模型分别研究了由曲线纤维复合材料和直线纤维复合材料构成的机翼颤振速度。分析结果表明,使用变刚度复合材料可以通过气动弹性优化得到更高的颤振速度。变刚度复合材料的优化空间可通过定义高阶非线性纤维方向和二维方向可变曲线纤维设计进一步增加，Stodieck等[19]以曲线纤维层合板矩形机翼为研究对象，研究了不同插值样本个数、优化铺层层数和二维角度优化对其颤振特性优化影响，研究表明，通过改变曲线纤维方向能够极大提高机翼气动弹性稳定性，减缓突风载荷。

本文以曲线纤维变刚度复合材料层合板构成的后掠机翼为研究对象，建立变刚度复合材料壁板颤振的气动弹性模型。研究了不同插值样本个数、优化铺层层数、角度厚度共同优化和二维角度优化对颤振速度的影响。

1 后掠机翼气动弹性模型

1.1 结构模型

本文采用变刚度曲线纤维复合材料梯形层合板作为后掠机翼的结构模型，其几何模型参数见图1，机翼几何、结构参数和材料属性见表1。

图 1 后掠机翼几何模型示意图

为了模拟被翼肋支撑的机翼蒙皮，数值仿真中假设机翼弦向刚性，即在弦向截面内不产生变形，仅沿展向产生弯曲扭转。为了简化弯扭耦合的影响，本文仅研究层合板纤维方向关于中性面对称的情况，后掠机翼由12层理想复合材料层合板构成，即层合板中不存在断裂、杂质等，并假设板厚度相对于弦向、展向可以忽略不计，此时层合板满足位移连续变化、小扰动和线性变形假设。

表1 后掠机翼几何、结构参数和材料属性

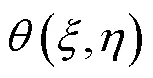
图2 后掠机翼相对坐标示意图

通过拉格朗日多项式拟合样本点纤维角度能够强制确保样本点纤维角度为人工定义角度，其余点纤维角度随样本点角度改变产生非线性变化，曲线阶次随着样本点数目的增加而提高。相对于其他拟合方式，如B曲线拟合等，拉格朗日多项式拟合更适用于样本点少于5个的情况，本文研究样本点个数为1至5，因此最终选择朗格朗日多项式拟合纤维方向。

1.2 气动力模型

飞行器的气动力计算，目前较为精确的方法为使用计算流体力学（CFD）对整个流场进行模拟，从而计算出飞行器表面的非定常气动力，然而CFD方法具有计算时间长，易发散等缺点。因此，本文使用高阶面元法计算飞行器表面的非定常气动力。相对于低阶面元法，高阶面元法精度更高，可较为准确模拟后掠机翼受到的非定常气动力。气动弹性计算时，通常需要计算出作用在气动单元上的非定常气动力，记作

由于气动力计算使用的气动网格与后掠机翼的结构模型通常节点、单元不一致，因此为了进行气动弹性的分析，需建立气动变形与结构的弹性变形之间的映射关系。一方面，通过样条插值方法将结构点的位移映射到气动模型的网格点上，另一方面，计算得到的气动力也通过样条插值传递到结构模型的节点上。根据参与插值的有限元模型的复杂程度，在进行插值时，不需要选取全部有限元节点，只需要选取能够表征结构主要模态的节点进行插值。结构变形与气动变形之间的转换关系可以写为

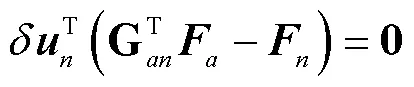
根据虚功原理，得到

1.3 气动弹性模型

通过方程(7)，得到了气动力在有限元节点上的等效载荷，运用拉格朗日方程，得到气动弹性方程

则得到广义模态坐标系下的气动弹性系统动力学方程

为简化上述气动伺服弹性方程，定义空气动力状态矢量为

合并方程(9)、方程(12)和方程(13)，气动伺服弹性系统可转化为如下状态方程形式

其中

2 后掠机翼颤振特性优化

本文优化参数为12层曲线纤维复合材料后掠机翼的纤维方向及铺层厚度，优化目标为后掠机翼达到最高颤振速度，主要研究内容由如下构成：1)研究曲线纤维层数对后掠机翼颤振特性优化影响；2)在层数固定时，研究层内样本点个数对后掠机翼颤振特性优化的影响；3研究相同层数和样本点时，铺层厚度对后掠机翼颤振特性优化的影响。

优化变量由不同铺层的样本点角度构成，对于优化层数为12层的对称曲线纤维复合材料层合板，每层设置样本点个数为5个时，优化变量总数为30个优化角度，每一个样本点纤维方向变化范围为0到180度。本文优化算法采用随机初始种群的遗传算法，优化种群个数随优化变量个数增加而增大，范围固定在50到200之间，以优化变量达到收敛条件或者达到200代结束。尽管遗传算法能够寻找多变量设计空间的全局优化结果，但其收敛性差导致结果可能并非最优结果，考虑该种情况下，每次优化计算采用不同初始种群多次优化寻找最优结果。

本文研究了三个不同的后掠机翼优化参数对提高颤振边界的影响，第一个优化参数为曲线纤维层合板数目，因为层合板沿中性面对称，相对于中性面两侧铺层的厚度、铺层角度等参数一致，因此对于沿中性面对称的12层层合板，仅有6层可单独优化，由于外部铺层对复合材料层合板弯曲刚度和弯扭耦合刚度影响更大，因此分别采用外部1层、3层、6层作为研究对象，未进行优化铺层的纤维方向固定为0度；第二个优化参数为每层的样本数，展向样本数变化范围为1(标准直线纤维)到5(4次方纤维方向变化)，同样弦向样本数变化范围为1(一维方向可变曲线纤维)或者3(二维方向可变曲线纤维)；第三个优化参数为单层复合材料层合板的厚度，优化时保证层合板厚度沿中性层对称，整体后掠机翼的厚度固定，即研究不改变质量情况下，各层厚度对后掠机翼颤振特性优化的影响。

2.1 不同铺层层数颤振特性优化

本节研究不同铺层数目优化对颤振边界的影响，该研究以优化外层1层作为标准对比对象，分别研究了优化外层1层、外层3层和外层6层所能够得到最高颤振边界的结果。每层中可优化样本数为5，其位置沿展向等间距分布，得到结果如表所示

表2 后掠机翼颤振速度随优化铺层层数的变化

可以发现，在铺层样本点数固定情况下，优化层数增加能够提高颤振边界的优化结果，优化层数为6时颤振边界相比优化层数为1时提高31.1%。优化外层3层相比优化外层1层提高颤振速度幅度较大，而优化6层相比优化外层3层提高幅度较小，由于外部铺层远离中性面，其弹性模量的变化对复合材料整体刚度影响最大，这与复合材料层合板理论相吻合，外层层合板对整体弯曲刚度、弯扭耦合刚度起到最主要影响，对于优化算法而言，优化6层的优化参数是优化3层参数的一倍，在此情况而言优化可选择最外半层即可。

图3 不同铺层层数优化时纤维方向随展向坐标变化

图3给出了样本个数为5时，选择不同优化层数后，纤维方向随展向坐标变化。图例中“2 of 6”表示总优化层数为6层时，提取优化结果的第二层纤维方向随展向坐标的变化。由数值计算结果可知，优化1层纤维方向与优化3层和6层最外层最优纤维方向类似，而优化3层纤维方向与优化6层时的外部3层最优纤维方向类似。这种情况下，为了减小优化变量，可以采用先优化外层1到2层，固定外层最优纤维方向后，再优化内层纤维方向。图4给出了优化外层1层时最外层纤维方向，可以发现纤维方向在翼根处存在较大的纤维方向变化，纤维角度在0到200mm内由50°急剧增大到160°，而在其余展长处纤维方向的变化较小，铺层方向与来流方向在XY平面内基本垂直。图5给出了优化1层时后掠机翼的颤振边界，可以发现该后掠机翼的第三阶模态为主要颤振模态，颤振形式为后掠机翼的第二、三阶弯扭耦合失稳。靠近翼根处纤维方向急剧变化能够增大模型在翼根处的扭转刚度，远离翼根处纤维方向有助于增大模型的弯曲刚度，因此该纤维方向有助于在合适的位置提高层合板的局部弯扭刚度，提高后掠机翼的颤振边界。图6和图7给出了优化6层时最外层纤维方向和后掠机翼的颤振边界，此时颤振主要模态为第二阶弯曲模态，颤振形式同样为第二三阶弯扭耦合失稳，因此优化后最外层纤维方向结果类似。

图4 优化1层时最外层纤维方向示意图

图5 优化1层时后掠机翼颤振边界V-G图

图6 优化6层时最外层纤维方向示意图

图7 优化6层时后掠机翼颤振边界V-G图

2.2 不同样本数颤振特性优化

本节仿真中固定优化铺层数为6，计算后掠机翼颤振速度随优化样本个数的变化。由表3结果可知，优化层数固定时，颤振边界随着样本个数的增加而提高，样本点个数为5时颤振速度相比样本点个数为1时提高14.3%。图8给出了不同样本个数优化后，最外层纤维方向随展向坐标变化，可以发现随着样本个数增加，纤维方向变化更加剧烈。文献[19]研究了大展弦比矩形板颤振速度随优化样本个数的变化，发现样本数增加至5个时可获得最高颤振速度，增加样本点数无法继续提高颤振边界。该现象在后掠机翼气动弹性模型中并未发现，原因是由于后掠机翼所受气动力沿展向波动较大，导致最优纤维方向沿展向变化幅度剧烈，因此达到最优纤维方向需较多样本点。图8显示最优优化角度波动较大，在此情况下增加样本点数依然有助于提高颤振边界。

表3 后掠机翼颤振速度随优化样本个数的变化

图8 不同样本个数优化最外层纤维方向随展向坐标变化

相比于沿展向一维角度优化，沿展向、弦向共同变化的二维角度优化能够再次提高颤振边界，考虑到优化变量个数问题，沿展向、弦向共同变化的二维角度优化仅选择优化层数3层，展向样本点数为5进行开展仿真。在其他条件相同的情况下，在展向样本点处沿弦向设置3个等间距样本点，即每层优化变量为15个，对于优化层数3层的情况下总共优化变量达到45个，优化后的后掠机翼最外层纤维方向如图9所示。二维角度优化仅相比一维角度优化时，在翼根和翼尖处沿弦向存在变化，此时颤振边界速度为27.27m/s，仅比沿展向一维优化提高1.7%，该结果和大展弦比矩形板得到结论与文献[19]一致且符合理论分析，对于曲线纤维构成的后掠机翼，沿展向角度优化对于提高弯曲刚度、弯扭耦合刚度等起到重要影响，因此能够较大幅度提高颤振边界速度。对于弦向优化、二维优化而言，大展弦比机翼沿弦向刚度较大，提高弦向刚度对颤振边界影响较小，可以忽略不计。

图9 二维角度优化时最外层纤维方向示意图

2.3 纤维方向和铺层厚度共同优化

本节重点研究曲线纤维纤维方向优化和厚度优化的关系，其中厚度优化时每层厚度变化但整体厚度保持一致，需要采用满足等式约束的遗传算法优化。首先研究纤维方向和厚度共同优化，对铺层6层进行优化结果见表4，对比表3可以发现采用纤维方向和厚度共同优化相比单独优化纤维方向能够更加有效提高颤振边界，以优化层数6层展向样本点5个为例，颤振边界提高5.4%。

表4 纤维方向厚度共同优化时后掠机翼颤振速度

图10给出了纤维方向厚度共同优化时，最外层纤维方向随展向坐标变化，对比纤维方向和厚度共同优化结果和单独纤维方向优化结果可以发现，厚度的改变对纤维方向影响较小，因此猜测纤维方向和厚度可单独优化。在该研究中，优化每层厚度时采用满足等式约束的遗传算法优化，能够保证优化后各单层铺层的厚度在人工给定的厚度之上，因此采用该方法在铺层厚度的工艺方面是可实现性的。

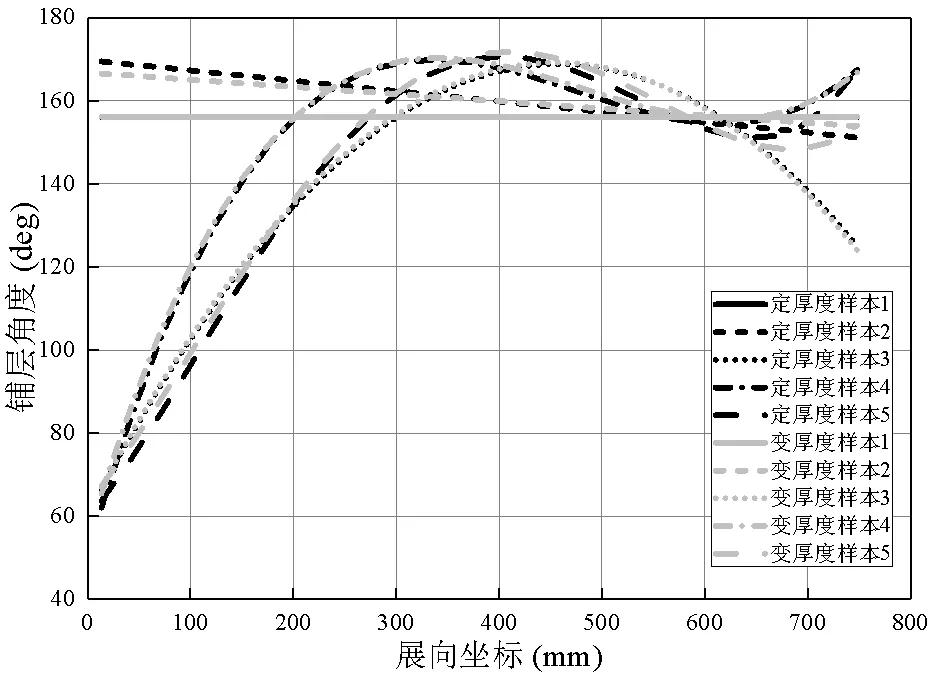
图10 纤维方向厚度共同优化时最外层纤维方向随展向坐标变化

随后对厚度单独优化，其纤维方向为该优化层数和样本个数条件下最优纤维方向，优化结果见表5，对比仿真结果发现，采用纤维方向和厚度分层次优化与纤维方向和厚度共同优化结果相差不大，如果考虑到优化变量个数问题，为了选取更高效率优化结果可以采用分层优化。

表5 纤维方向厚度分步优化时后掠机翼颤振速度

3 结论

本文研究了曲线纤维层合板构成的后掠机翼中纤维方向和厚度的改变对颤振边界的影响。根据数值仿真发现：1)后掠机翼外部铺层优化角度对颤振速度影响更大，本文中考虑到计算效率等因素推荐选择优化3层铺层即优化铺层占整体铺层的一半；2)后掠机翼沿展向最优角度相比于大长细比矩形复合板变化剧烈，因此颤振速度在较大样本个数范围内随着样本个数的增加而提高；3)后掠机翼沿展向优化纤维方向对结果产生较大影响，而不需要采用沿展向和弦向的二维纤维方向优化算法；4)后掠机翼纤维方向和厚度共同优化能够再次提高颤振边界，选择分步优化即先优化纤维方向后优化厚度，可以在几乎不增加计算量的情况下提高颤振边界。

后续工作将开展结构更为复杂的曲线纤维层合板后掠机翼的颤振特性优化，采用更为精确的气动力开展气动弹性计算分析。目前技术已可实现复合材料曲线纤维的铺层加工，随着技术的引进，曲线纤维复合材料的优化对提高材料刚度等方面产生重要影响。

[1] Weisshaar T A. Aeroelastic tailoring of forward swept composite wings[J]. Journal of Aircraft, 1981, 18(8): 669-676.

[2] Shirk M H, Hertz T J, Weisshaar T A. Aeroelastic tailoring theory, practice, and promise[J]. Journal of Aircraft, 1986, 23(1): 6-18.

[3] Eastep F E, Tischler V A, Venkayya V B. et al. Aeroelastic tailoring of composite structures[J]. Journal of Aircraft, 1999, 36(6): 1041-1047.

[4] Weisshaar T A, Duke D K. Induced drag reduction using aeroelastic tailoring with adaptive control surfaces[J]. Journal of Aircraft, 2006, 43(1): 157-164.

[5] Pettit C L, Grandhi R V. Optimization of a wing structure for gust response and aileron effectiveness[J]. Journal of Aircraft, 2003, 40(1): 1185-1191.

[6] Kim T U, Hwang I H. Optimal design of composite wing subjected to gust loads[J]. Computers & Structures, 2005, 83(19-20): 1546-1554.

[7] Arizono H, Isogai K. Application of genetic algorithm for aeroelastic tailoring of a cranked-arrow wing[J]. Journal of Aircraft, 2005, 42(2): 493-499.

[8] Kameyama M, Fukunaga H. Optimum design of composite plate wings for aeroelastic characteristics using lamination parameters[J]. Computers & Structures, 2007, 85(3-4): 213-224.

[9] Guo S. Aeroelastic optimization of an aerobatic aircraft wing structure[J]. Aerospace Science and Technology, 2007, 11(5): 396-404.

[10] Guo S, Li D, Liu Y. Multi-objective optimization of a composite wing subject to strength and aeroelastic constraints[J]. Journal of Aerospace Engineering, 2012,226(G9): 1095-1106.

[11] 谯盛军, 高行山, 王富生. 全复材机翼桁条的结构布局和尺寸对刚度的影响分析[J]. 强度与环境, 2014, 41(1): 50-56. [Qiao Shengjun, Gao Hangshan, Wang Fusheng. The influence analysis of stiffness on stringer layout and dimension of full composite wing [J]. Structure & Environment Engineering , 2014, 41(1)：50-56.]

[12] 张钧然, 王富生, 岳珠峰. 基于CFD/CSD耦合技术的复合材料机翼操纵效率分析[J]. 强度与环境, 2015, 42(2): 45-51. [Zhang Junran, Wang Fusheng, Yue Zhufeng. Control efficiency analysis of aircraft wing based on CFD/CSD coupling technique[J]. Structure & Environment Engineering , 2015, 42(2)：45-51.]

[13] Lopes C S, Gurdal Z, Camanho P P. Variable-stiffness composite panels: buckling and first-ply failure improvements over straight-fibre laminates[J]. Computers & Structures, 2008, 86(9): 897-907.

[14] Gurdal Z, Tatting B F, Wu C K. Variable stiffness composite panels: effects of stiffness variation on the in-plane and buckling response[J]. Composites Part A: Applied Science and Manufacturing, 2008, 39(5): 911-922.

[15] Lopes C S, Gurdal Z, Camanho P P. Tailoring for strength of composite steered-fibre panels with cutouts[J]. Composites Part A: Applied Science and Manufacturing, 2010, 41(12): 1760-1767.

[16] Honda S, Narita Y. Natural Frequencies and vibration modes of laminated composite plates reinforced with arbitrary curvilinear fiber shape paths[J]. Journal of Sound and Vibration, 2012(1): 180-191.

[17] 杜宇, 杨涛, 李志猛, 等. 纤维曲线铺放的变刚度复合材料层合板的失效分析[J]. 宇航材料工艺, 2013, 43(5)：22-25.[Du Yu, Yang Tao, Li Zhi-meng, et al. Failure analysis of variable-stiffness composite laminates with curvilinear fiber placement[J]. Aerospace Materials & Technology , 2013, 43(5): 22-25.]

[18] Haddadpour H, Zamani Z. Curvilinear fiber optimization tools for aeroelastic design of composite wings[J]. Journal of Fluids and Structures, 2012, 33(1): 180-190.

[19] Stodieck O, Cooper J, Weaver P. Optimization of tow-steered composite wing laminates for aeroelastic tailoring[J]. AIAA Journal, 2015, 53(8): 2203-2215.

[20] M Karpel, E Strul. Minimum-state unsteady aerodynamic approximations with flexible constraints[J]. Journal of Aircraft, 1996, 33(6): 1190-1196.

Aeroelastic Tailoring of the Swept-back Wing made of Composite Laminates with Curvilinear Fiber

YANG Zhi-jun1YU Yang2GAO Bo1GUO Jing1

（1 Science and Technology on Reliability and Environmental Engineering Laboratory, Beijing Institute of Structure and Environment Engineering, Beijing 100076, China; 2 Beijing Institute of Structure and Environment Engineering, Beijing 100076, China）

The manufacture for laminates with curvilinear fibers is a new technology for manufacturing composite laminates with variable stiffness. In this paper, the swept-back wing of 12-layer composite laminates with curvilinear fiber is studied. Aeroelastic tailoring of the swept-back wings in incompressible flow and the effects of fiber angle, optimal layer numbers and layer thickness on flutter characteristics are analyzed. In the numerical simulations, the structural model and aerodynamic model of the swept-back wing are established by finite element method and higher order panel method, respectively. The flutter boundary of the swept-back wing is computed via VG method. The results show that the flutter speed of the swept-back wing made of all laminates with curvilinear fiber is 31.1% higher than that made of only the outer layer with curvilinear fiber, and 14.3% higher than that made of laminates with linear fiber. The flutter velocity with two-dimensional fiber angle variations used is only 1.7% higher than that with one dimensional fiber angle variations used, which proves that the variable fiber direction along the span-wise direction has a greater influence on the flutter boundary. When fiber angles and thickness are optimized together, the flutter velocity of the swept-back wing can be increased by 5.4% without changing its overall thickness. The results show that the design ability of the aeroelastic tailoring can be further improved via using composite laminates with curvilinear fibers. The flutter characteristics of the composite swept-back wing can be significantly changed by adjusting the path of curvilinear fibers.

Aeroelastic tailoring; Curvilinear fibers; Variable stiffness composite laminate; Higher order panel method

V414.8

A

1006-3919(2022)02-0034-08

10.19447/j.cnki.11-1773/v.2022.02.005

2021-09-15；

2021-12-25

国家自然科学基金（11502023、11502024）

杨执钧（1991—），男，博士，工程师，研究方向：气动弹性分析与控制；（100076）北京9200信箱72分箱.