焊缝尺寸对焊接金属波纹管刚度的影响研究

冯震 聂帅 田纪云 马世华 胡婷婷

焊缝尺寸对焊接金属波纹管刚度的影响研究

冯震 聂帅 田纪云 马世华 胡婷婷

（北京航天动力研究所，北京 100076）

基于焊接金属波纹管各切片金相图的焊缝尺寸测量数据和有效熔宽及熔深拟合数据，进行2D轴对称全模型绘制并使用有限元分析方法开展焊缝尺寸对焊接金属波纹管刚度的影响研究。研究发现焊缝尺寸和膜片之间的贴合干涉现象对焊接金属波纹管的刚度影响较大，焊缝尺寸越小则焊接金属波纹管整体刚度越大，压缩距离增大会导致膜片之间的贴合干涉现象加剧致使波纹管刚度增大。

金属波纹管；焊缝尺寸；压缩距离；刚度

0 引言

波纹管补偿器通过调节波纹压缩位移量，实现各工况下产生的机械位移、热膨胀的补偿[1-2]。其工作原理为依据焊接金属波纹管两侧气液腔压力变化自动改变初始压缩距离，进而完成液腔中工质挤出量的调节。因此焊接金属波纹管的整体刚度大小是不同工况下压缩位移自动调节功能实现的关键因素，直接决定金属波纹管补偿器性能的优劣。焊接金属波纹管的整体刚度受膜片尺寸、波形及波数等众多参数影响。黄笑梅、王占生等[3-5]结合仿真及试验的方法开展了金属膜片厚度、波数、波形对焊接金属波纹管的刚度影响研究。焊接金属波纹管的膜片材料属性及接触也会对焊接金属波纹管组的整体弹性产生影响。娄路亮、刘江等学者[6-7]从金属膜片的材料本构方程及接触方面开展焊接金属波纹管刚度的影响研究。除此之外，焊接金属波纹管上下膜片之间的焊接形式及形貌对波纹管强度有影响。王升林、Stephen O、Zhang D K等[8-10]开展了焊接接头形貌对焊接金属波纹管受力情况的影响研究。目前焊接金属波纹管刚度的有限元分析，通常采用单组波的模型进行仿真计算并用单组波计算获得的刚度值除以整体波数后获得的刚度值作为整体焊接金属波纹管的刚度值，此方式忽略膜片之间贴合干涉带来的刚度差异。还有一些仿真计算虽然是进行全波数建模，计算其整体刚度。但是未考虑同一焊接金属波纹管不同焊接波组之间焊接尺寸的差异性。本文结合焊接金属波纹管各膜片切片有效熔宽、熔深统计数据，完成不同焊接尺寸的焊接金属波纹管整体2D轴对称建模。依据X光影像确定焊接波纹管上下膜片贴合部位并在仿真时对贴合部位设置非线性接触，解决以往焊接尺寸和上下膜片贴合情况未知造成仿真计算刚度与实测刚度偏差较大的问题。通过实验数据和有限元仿真结果的对比与分析，开展焊缝尺寸对焊接金属波纹管整体刚度的影响研究。

1 焊接金属波纹管刚度差异对比

1.1 焊接金属波纹管简介

焊接金属波纹管属于薄壁轴对称结构，由厚度0.2mm的双正弦型金属膜片通过氩弧焊焊接而成，其中金属膜片采用AM350不锈钢板压制而成。通过氩弧焊焊枪先两、两焊接金属膜片内圆焊缝，再进行焊接外圆焊缝，其中内圆、外圆焊缝均为等厚端接焊缝，最后焊接上下封头形成完整的焊接金属波纹管。焊接金属波纹管具有良好的密封性和抗力学振动特性且能有承受较大的压力。因其金属膜片较薄使其整体轴向刚度较小，在受到较小内外压差下均能调整压缩量，因此具有较好的动作灵活性和挤出性能。

图1 焊接波纹管组件实物图

1.2 焊接金属波纹管理论计算和实测刚度对比

焊接金属波纹管依据内外侧气液腔压差实现轴向伸缩，因此焊接金属波纹管的轴向刚度对焊接金属波纹管整体性能十分重要。国内外常采用下述的波纹管理论刚度计算公式[11]来预估整体金属波纹管的刚度

式中为波纹管组件刚度，N/mm；为材料弹性模量，MPa；m为膜片中径，mm；为膜片厚度，mm；为波数；为膜片宽度，mm；o为膜片外径，mm；i为膜片内径，mm；对该型号的金属膜片产品进行随机抽样并测量其内外径尺寸及厚度。抽样件膜片测量参数如表1所示。

表1 金属膜片抽样尺寸参数

通过对抽样结果分析可知该型号金属膜片产品内外圆尺寸及厚度一致性较好，可知大部分膜片外圆尺寸应该为230.96mm，内圆尺寸在190.52mm，厚度为0.202mm。按照上述公式计算其焊接金属波纹管刚度，该型号不同批次的焊接金属波纹管刚度应为2.387N/mm。通过统计该同型号不同批次的焊接金属波纹管实测刚度并与该型号金属波纹管理论计算刚度进行对比，发现13台焊接金属波纹管刚度散度较大。焊接金属波纹管实测刚度偏离理论计算刚度情况如图3所示。

图3 不同批次焊接金属波纹管组件刚度

通用理论刚度计算公式获得的刚度和图3不同批次产品刚度分布分析可知除材料参数、波数及膜片尺寸数据外还有其他因素对焊接金属波纹管的刚度影响较大。通过对比分析不同批次产品的生产记录数据发现不同批次产品的焊缝熔宽尺寸有差别。

1.3 焊缝尺寸对压缩端约束反力的影响研究

在该波纹管膜片焊接时保持焊枪的速度、电流及电压的一致性可保障焊接处焊缝的质量满足要求。参照该型号产品焊接速度、电流及电压等工艺要求进行膜片试焊并对焊接结构进行金相检查，其焊缝形貌如图4所示。对试焊件膜片组内外圆焊缝尺寸参数进行测量发现内外圆焊缝熔宽及熔深在不同的范围内，具体如表2所示。

表2 试焊件膜片组有效熔宽与熔深

根据上下限焊缝的熔深和熔宽分别绘制两组膜片焊接结构并进行仿真计算，下限焊缝尺寸结构对应小焊头，上限焊缝尺寸结构对应大焊头。对两种尺寸对应的大小焊头模型进行下端固定约束，上端压缩位移均为1mm。获得上端压缩位移处的支反力结果图5和图6所示，其中下限焊缝尺寸结构的焊头处变形为0.0506mm、支反力为185.69N，上限焊缝尺寸结构的焊头处变形为0.0518mm、支反力为178.11N。通过不同焊头尺寸结构在相同条件下的变形情况可知相比于大焊头，小焊头的变形量较小且正弦波型附近的变形有较大影响。因此小焊头会提高单组焊接金属膜片组整体的刚度。由胡克定律可知在相同压缩位移下，所需压缩力越大则结构刚度越大。因此下限焊缝尺寸结构（小焊头）刚度（Min=185.69N/mm）大于上限焊缝尺寸结构（大焊头）刚度（Max=178.11N/mm）。因此证明焊缝尺寸差异对焊接金属波纹管的整体刚度有较大影响。

2 焊缝尺寸对整体刚度的影响研究

2.1 焊缝有效熔宽与熔深的关系

选取该型号某台产品的焊接金属波纹管进行等间隔焊接膜片组标记及排序（13处），并测量标记处的内外圆焊缝有效熔宽，如表3所示。

然后对标记处的膜片组进行切片并做金相检查，然后测量不同标记处的焊缝有效熔深。最后根据所测得的有效熔宽和熔深数据进行内外圆焊缝熔宽和熔深的关系拟合获得内外圆焊缝熔宽和熔深的拟合曲线，拟合曲线如图7所示。

表3 内外圆焊缝熔深熔宽对应表

2.2 全焊缝形貌的建模及计算

对某批次产品进行熔宽测量并根据上述焊缝熔宽与熔深拟合关系式计算该条焊缝的熔深数值，最后依据熔深和熔宽数值进行全模型焊接金属波纹管建模。对同批次产品充压使其有一定压缩位移后进行X光检测，根据影像结果设置仿真模型中焊接金属上下膜片接触位置。在小冲压压力下即小压缩量下，内外焊缝焊菇上下膜片夹缝处无明显贴合情况，在压缩量增大上下膜片在膜片焊接直线段处开始贴合，且贴合情况不同。仿真计算中对全模型内外焊接直线段贴合位置设置接触，接触类型为frictionless。计算模型进行下端固定，计算11种压缩距离下上端压缩约束处的约束反力。

在给定的各压缩距离下发现焊接金属波纹管在受压时各膜片之间存在贴合干涉问题，该贴合干涉的存在导致膜片变形和受力发生变化。75mm和95mm压缩距离下的焊接金属波纹管上下膜片贴合干涉情况如图8所示。

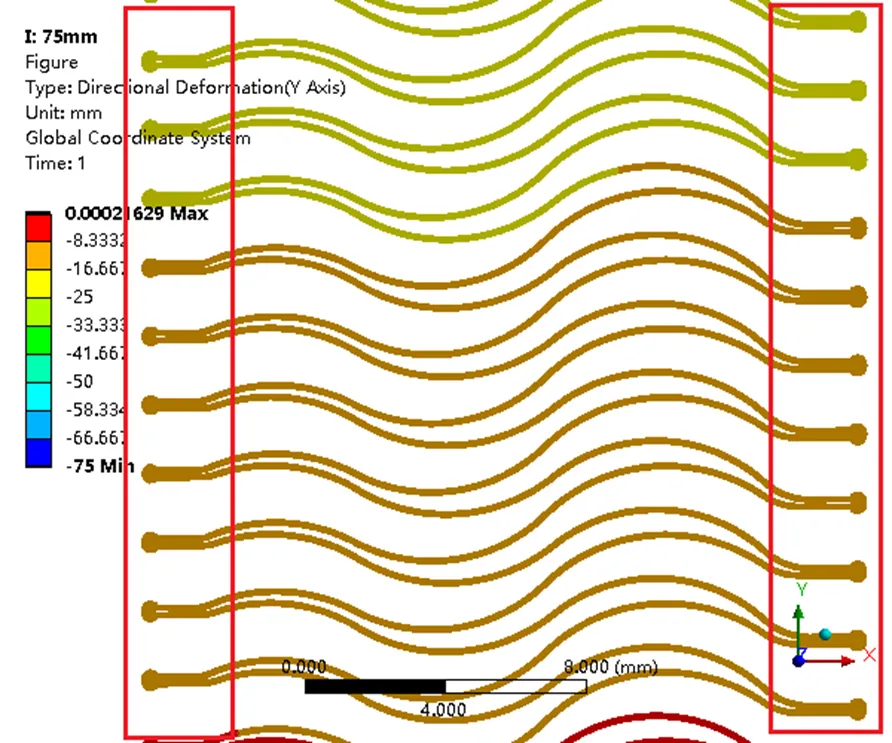
图8中红色线框为上下膜片内外圆焊头附近直线段膜片部位，通过对比分析可知上下膜片内外圆焊头附近直线段膜片部位贴合情况不同。同一压缩距离下不同部位膜片组的贴合干涉情况存在差异，不同压缩距离下的同区域膜片贴合干涉情况也存在不同。

对比不同压缩量下相同内外焊缝位置的应力，发现同一组内外膜片，外圆焊缝整体应力小于内圆焊缝，对于内圆焊缝，焊缝直线段膜片外侧应力大于焊缝直线段膜片夹缝内侧应力。对于外圆焊缝，焊缝直线段膜片外侧应力小于焊缝直线段膜片夹缝内侧应力。从小压缩量（5mm）和大压缩量（85mm）相同焊缝位置的应力分布趋势相同。因此可知随着压缩量的增大，相同位置的应力结果也逐渐增大。在较大的应力下，上下膜片夹缝之间的间隙减小进而产生贴合进而导致焊接波纹管刚度增大。应力分布结果如图9和图10所示。

采用弹簧试验机对焊接金属波纹管整体刚度进行测量。通过给定不同的压缩距离和获得相应压缩距离下对应的弹簧力。该批次焊接金属波纹管各压缩距离和弹簧反力实测值的关系如图11所示。依据上述仿真计算获得的相同11组压缩距离下的支反力与对应压缩位移下的实测弹簧力对比，对比图如图12所示。

通过图11和图12分析可知在压缩距离为75mm内，压缩距离和弹簧力成正比例关系。压缩距离在75mm至105mm之间时，随着压缩距离的增加波纹管上下膜片之间贴合干涉现象严重致使弹簧力急剧增大。其中在压缩距离为105mm时，实测弹簧力（254MPa）和仿真计算值（241.81MPa）之间的误差为4.7%。

图11 压缩距离与弹簧力关系图

图12 实测-仿真压缩距离与弹簧力对比图

3 结论

1) 通过对单组焊接波纹管仿真分析，发现焊缝尺寸大小对焊接金属波纹管整体刚度影响较大，焊缝尺寸越小焊接金属波纹管整体刚度越大。除此之外同条焊缝的熔宽值和其对应的熔深值存在正相关关系。

2) 通过对含不同焊接接头的全波数波纹管模型进行仿真分析，发现焊接金属波纹管在一定压缩距离下膜片之间存在贴合干涉现象。随着压缩距离的增大，上下膜片贴合干涉现象加剧致使整体波纹管刚度增大。

3) 通过对比不同压缩量下相同位置处内外焊缝应力情况，发现同一组内外膜片中外圆焊缝附近区域应力小于内圆焊缝附近应力。随着压缩量的增大，相同位置的应力也逐渐增大。上下膜片焊接形成的夹缝间隙减小进而产生贴合，导致在大压缩量下焊接波纹管刚度增大。

[1] 倪洪启, 李祥瑞, 王树强, 等. 波纹管补偿器加压变形的有限元分析[J]. 机械工程师, 2015(3): 78-79.[NI H Q, LI X R, WANG S Q, et al. Finite element analysis of compression deformation of bellows compensator [J]. Mechanical engineer, 2015(3): 78-79.]

[2] 徐至煌. 波纹管补偿器安全状态可靠性计算及软件开发应用[J]. 石油化工设备, 2020, 49(4): 33-38.[XU Z H. Safety state reliability calculation and software development and application of bellows compensator [J]. Petrochemical equipment, 2020,49 (4): 33-38.]

[3] 阿斯耶姆·肖开提.多层焊接金属波纹管刚度实验与数值计算对比分析[J]. 机械设计与研究, 2014, 12(6): 48-50.[Asyam shokaiti. Comparative analysis of stiffness experiment and numerical calculation of multilayer welded metal bellows [J]. Machine Design and Research, 2014, 12(6):48-50.]

[4] 黄笑梅,芮训诚. 影响焊接波纹管刚度及承压能力的参数研究[J]. 机械设计与制造, 2014, 11(1): 34-37. [Huang X M, Rui X C. Research on parameters affecting the stiffness and pressure bearing capacity of welded bellows [J]. Mechanical design and manufacturing, 2014,11 (1): 34-37.]

[5] 王战生. 焊接波纹管接头设计分析[J]. 机械制造文摘(焊接分册),2019, 3: 23-27.[Wang Z S. Design and analysis of welded bellows joint [J]. Abstract of mechanical manufacturing (welding volume), 2019,3: 23-27.]

[6] 娄路亮, 胡晓军, 隋国发, 等. 焊接波纹管的非线性力学分析与试验研究[C]. 第九届全国膨胀节学术会议,安徽:中国压力容器学会膨胀节委员会、合肥通用机械研究院,2006: 13-19.

[7] 刘江, 殷明霞, 周宏, 等. 多层波纹管结构参数与轴向刚度关系研究[J]. 强度与环境, 2016, 43(6): 24-28.[Liu J, Yin M X, Zhou H, et al. Study on the relationship between structural parameters and axial stiffness of multilayer bellows [J]. Structure & Environment Engineering, 2016, 43 (6): 24-28.]

[8] 王升林, 冯震, 刘士杰, 等. 焊接结构对某型金属波纹管使用寿命的影响分析[J]. 强度与环境, 2021, 48(1): 32-41.[WANG S L, FENG Z, LIU S J, et al. Analysis on the influence of welded structure on the service life of a certain type of metal bellows [J]. Structure & Environment Engineering [J]. 2021, 48(1):32-41.]

[9] Stephen O, Jeffrey L. Failure analysis of a metal bellows flexible hose subjected to multiple pressure cycles[J]. Engineering Failure Analysis, 2012, 22: 11-22.

[10] Zhang D K , Zhao Y , Dong M Y , et al. Effects of weld penetration on tensile properties of 2219 aluminum alloy TIG-welded joints[J]. Transactions of Nonferrous Metals Society of China, 2019, 29(6): 1161-1168.

[11] 李志强, 马咏梅, 朱涛, 等. 机械密封焊接波纹管波片的应力计算及分析[J]. 化工机械, 2019, 6(6): 36-41.[Li Z Q, Ma Y M, Zhu T, et al. Stress calculation and analysis of wave plate of mechanical seal welded bellows, chemical machinery [J]. 2019, 6(6): 36-41.]

Study on the Effect of Weld Size on the Stiffness of Welded Metal Bellows

FENG Zhen NIE Shuai TIAN Ji-yun MA Shi-Hua HU Ting-Ting

(Beijing Aerospace Propulsion Institute, Beijing 100076,China)

Based on the measurement data of weld size and morphology of each slice of welded metal bellows and the fitting relationship data between effective weld width and penetration depth, the 2D axsymmetric full model is drawn, and the influence of weld size on the overall stiffness of welded metal bellows is studied by finite element analysis method. It is found that the weld size and the bonding interference between the upper and lower diaphragms have a great impact on the stiffness of the welded metal bellows. The smaller the weld size, the greater the overall stiffness of the welded metal bellows. The increase of the compression distance will aggravate the bonding interference between the upper and lower diaphragms, resulting in the increase of the stiffness of the welded metal bellows.

Welded metal bellows; Weld size; Compression distance; Stiffness

V416

A

1006-3919(2022)02-0008-07

10.19447/j.cnki.11-1773/v.2022.02.002

2022-01-25；

2022-03-04

冯震（1978—），男，高工，研究方向：空间温控系统与热控流体回路；（100076）北京市9200信箱11分箱.