“轴对称”教法探析

孙静娴

[摘 要]轴对称图形的性质并不难理解，学生通过对图形的观察与分析，也能发现一些特征，但是只有经历知识的整个建构过程，通过观察、操作、对比、辨析，才能实现对知识的深刻理解与领会。

[关键词]轴对称;情境;任务;空间想象

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2022）11-0048-03

“轴对称”一课，教学目标是让学生通过单独画图、合作探究、交流探讨等，认清轴对称图形的主要特征，指引学生研究、概括、描述出轴对称图形的各种性质，并学会根据相关性质画出标准的轴对称图形;教学重点是加深学生对轴对称图形特征的认识和理解，促使学生发现和归纳轴对称图形的各种性质;教学难点是让学生找到对应点并理解对应点到对称轴等距的结论，能根据轴对称图形的各种性质画出标准的轴对称图形。

一、创设情境，激趣导入

师：英国剑桥大学是世界著名学府，也是学子们梦寐以求的学习圣地。老师这里有一道剑桥大学的全球招生考试题，你们想不想一试身手？

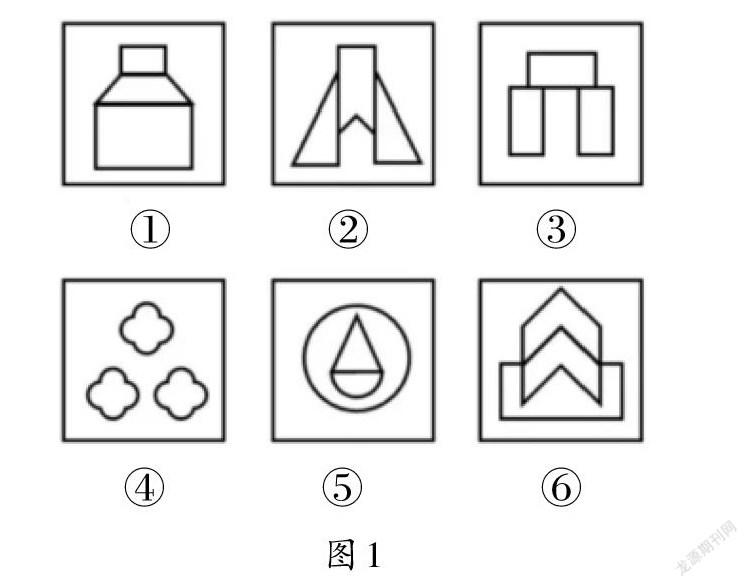
动画演示题目：将以下6个图案（如图1）分为两类，每类图案都有各自的特征或者规律。

【设计说明：通过一道剑桥大学的全球招生考试题导入新知，最大限度地吸引学生的眼球，激发学生的学习兴趣，激活学生的认知经验、求知欲和好奇心。】

二、任务驱动，探究新知

1.指定对称轴，画出轴对称图形的另一半

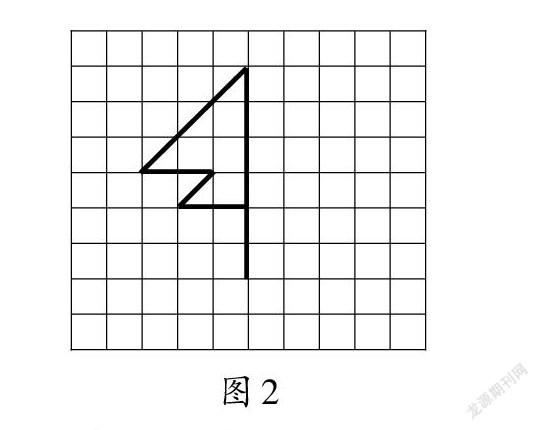
教师指定好一条对称轴，同时给出轴对称图形的左边图案，让学生补全右边图案（如图2）。

个人独立完成的任务：

（1）想象构思右边的图案;

（2）尝试画出右边的图案。

合作探究完成的任务：

（1）互相评判对方所画的图形是否是轴对称图形;

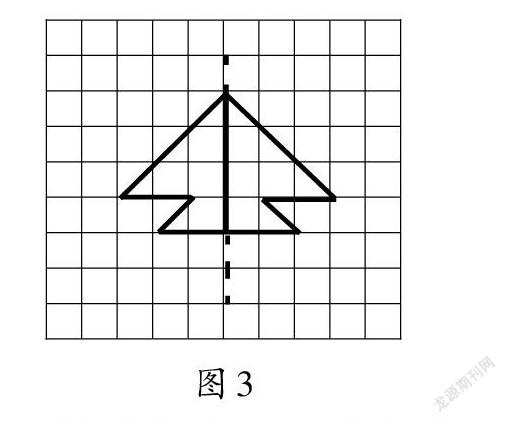
（2）向对方解说自己画图的详细流程和方法。学生按照教师的指示补全图案，完整的图案看起来像一条“小鱼”（如图3）;

（3）反馈交流。定好轮廓上的重要顶点，沿着对称轴在另一边描出对应顶点，然后将所有新画出的对称顶点顺次连线。经过观测发现，每组对应点到对称轴的距离相等。

【设计说明：借助方格图这个有力的“画布”，可以清晰地展示轴对称图形的各种性质，同时使得蕴含在轴对称图形中的各种数据、几何位置的特性都一一暴露出来，长度相等的数据特征和对应点的连线与对称轴垂直的几何特征也都呈现在学生眼前，学生的认知经验在实践中得到了进一步丰富。学生在画图中完成感性认知，在判断中完成理性认知，在解说中完成智性认知，有关结论都是学生自己归纳总结出来的，是学生思维发展的成果。但是依靠方格图，学生只会抽象地感知格数相等，借此判断距离相等，要想让学生认识到实际长度相等，还需要进一步引导。】

2.隐藏对称轴，画出轴对称图形的另一半

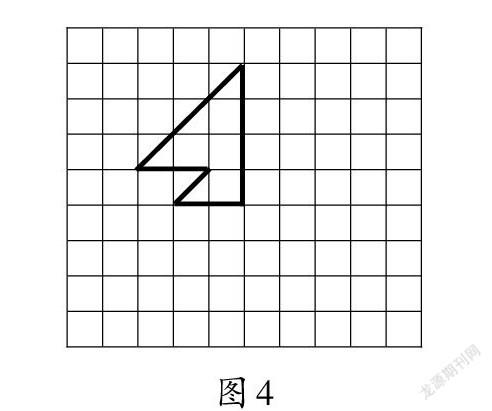
师：除了这条对称轴，还有没有别的对称轴，如果改换对称轴，画出的又会是什么图形？

课件演示：[ ]

个人独立完成的任务：

（1）定——自定义对称轴;

（2）想——参照新的对称轴想象出另一半图案的轮廓;

（3）画——画出另一半图案。

合作探究完成的任务：

（1）交互裁决，判别所画的图形是否是轴对称图形;

（2）介绍解说，各自陈述自己的画法和流程;

（3）分类整理，将组内各种图案作品归类存放。

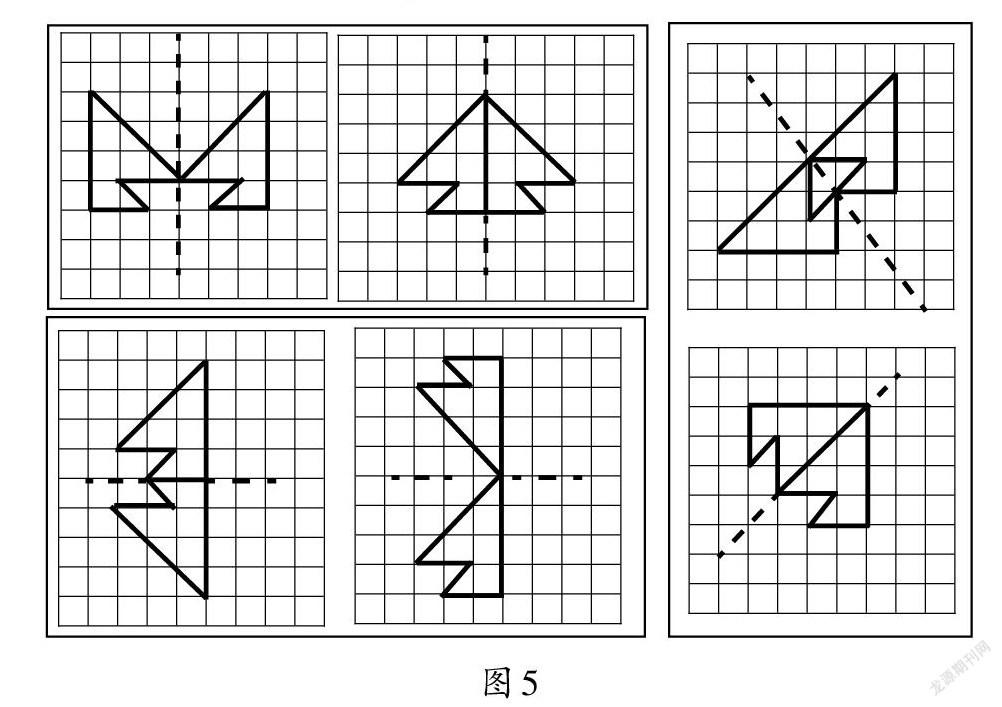
学生绘制的作品主要有以下几种（如图5），共分为三类。教师指引学生观察后总结出：对称轴的方位有别，据此画出的轴对称图形的全貌也有差异。但是，无论是哪种画法，各图形中的对应点与对称轴间隔的格数都相等。

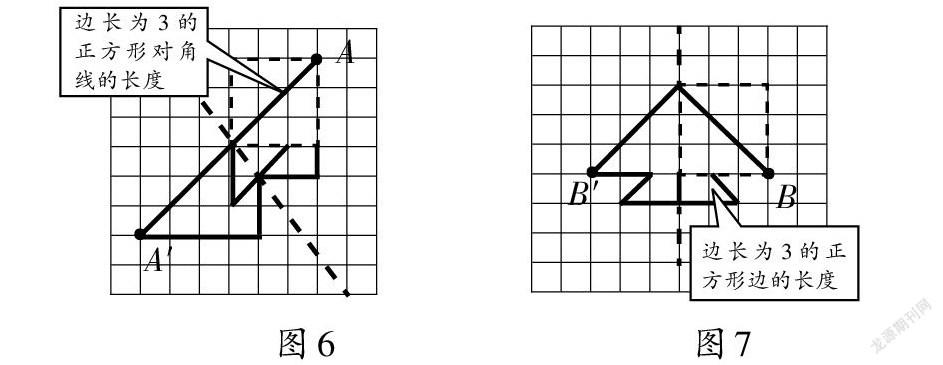
生1（对比图6和图7）：图6中的对应点 A 与 A'距离对称轴3格。

师：图6中的这个3格间距与图7中 B 和 B'到对称轴的3格间距是否一样？

生2：图6中的3格间距其实是3个方格形成的正方形的对角线，而图7中的3格间距则是3个方格形成的长方形的边长，虽然方格跨度相等，但是实际长度不同，因此用“对应点到对称轴间隔的格数相等”表述不严谨，存在歧义，应订正为“对应点到对称轴的距离相等”。（以下简称“对应点等距”）

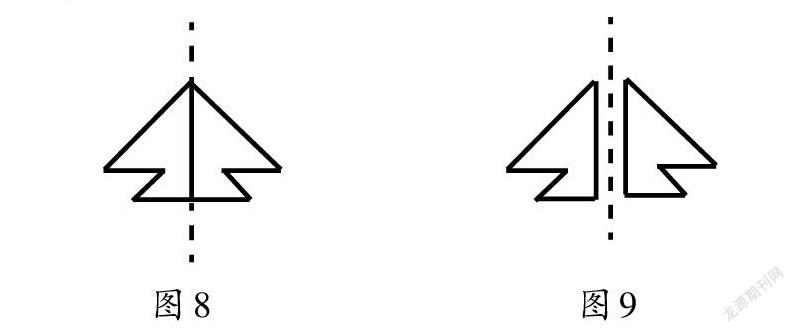
师（用动图模拟裁纸刀，顺着对称轴裁开图7，继续用动图连贯演示右边图形向右平移3格）：如果继续保持和左边图形的轴对称关系，该怎么做？（学生提出两种方案，要么同向平移对称轴，要么反向平移另一边的图形）综合来看两个图形（如图8和图9），有什么相同点和不同点？

生3：图8可以看作一个轴对称图形，或者说一个图形存在轴对称性质，而图9则是两个图形呈轴对称关系，总的来说，它们都是关于某条轴对称，两种情形下的图形统称为轴对称图形。（教师单独补写“轴”字，完善和揭示课题）至此，一个轴对称图形到两个图形成轴对称关系的衔接与切换已经平稳完成。

【设计说明：对于竖直和水平方向的轴对称图形，由于受到方格十字交叉线的干扰，学生仍是将对应点到对称轴的距离用“格数”这个界限模糊的词来形容。因此，出现其他倾斜角度的对称轴时，“格数”已经不再能代表距离长短。于是教师抓住这一“变异”进行深挖，重点解析，在此基础上引导学生讨论、辨析、修正，得出“对应点到对称轴的距离相等”这一严谨表述。同时，为了丰富和完善学生对轴对称图形的认识，教师因势利导，将“小鱼”图形对半剖开，通过先破坏对称性，然后借助平移对称轴或者平移另一半图形来继续达到对称状态，引发学生反思，自然而然地完成一个轴对称图形向两个图形成轴对称关系的转换，大大丰富了轴对称的含义，而学生对轴对称的理解也更为全面和通透。】

三、应用对称，强化空间想象力

师：在“小鱼”的旁边有一块石头和一片树叶，你能画出它们的对称图形吗？（说明：石头尚在方格图中，而树叶则偏离了方格图）

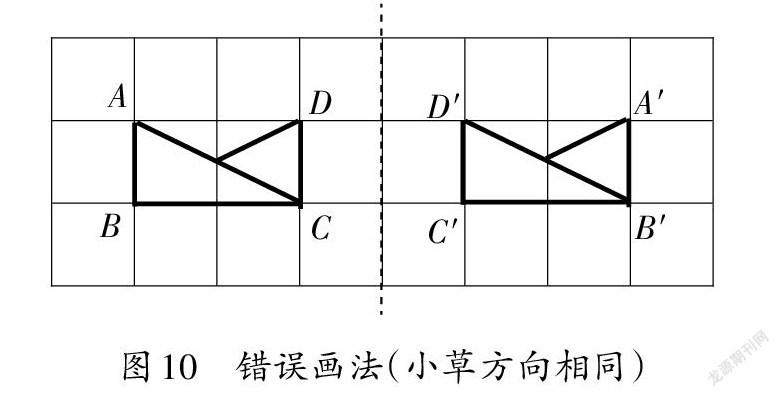
师（从学生的作业中挑出典型错例，开展讲评，如图10）：尽管对应点到对称轴的直线距离相同，但是各对应点的连线错乱。原图是 A点连 C点，新作的对称图却是D'点连B'点，应该是A'点连C'点。

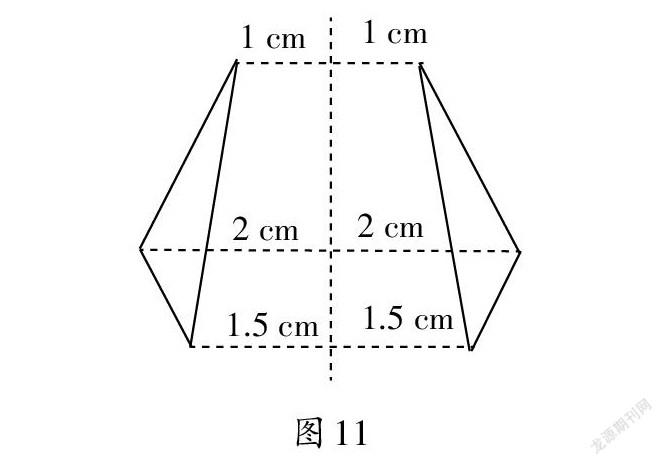
（请画对树叶轴对称图形的学生现场解说，如图11）生：对应点到对称轴的距离相等，对应点连线与对称轴所在直线成垂直关系。

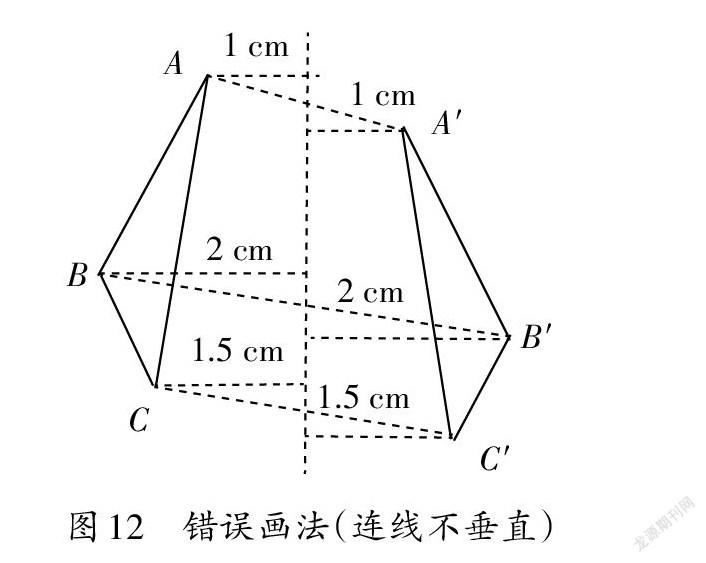
师（出示图12）：即使满足对应点等距，但是连线没有垂直于对称轴，仍然得不出轴对称图形。

【设计说明：学生有了足量的活动经验，几乎都能完成小草的轴对称图形，但出现了“连线错误”的新型错误。于是教师给出专项纠正练习，这既是对“对应点等距”的巩固，又是对连线错误的预防。怎样做才能显露轴对称的主要特性——对应点等距呢？最好的做法就是舍弃方格图，只有戒除这个依赖，学生的认知才会深刻。让学生在白纸上画出树叶的轴对称图形的这一举措让学生对轴对称图形的认识更加清晰，“对应点等距、连线垂直”这一结论的得出也就水到渠成了。】

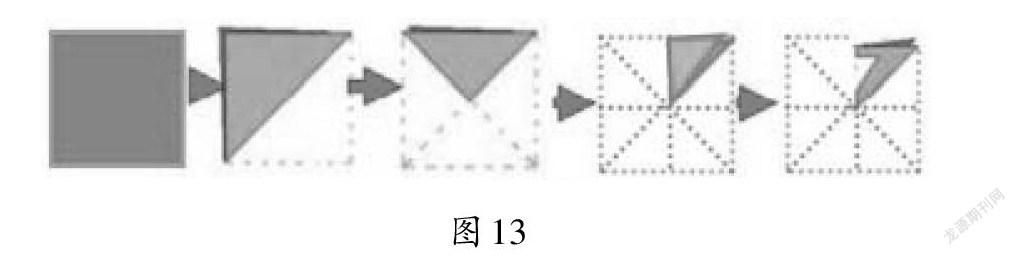
师（出示图13）：按照图示，想象这张纸剪去一块后的展开图。

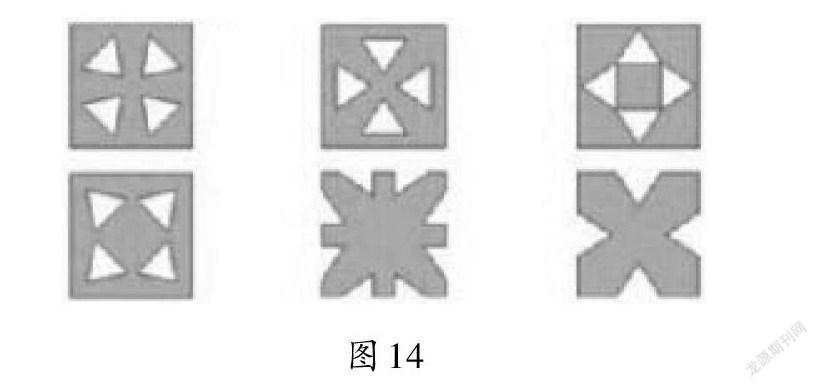
师（出示图14）：你选哪个？说明理由。重点围绕“对称轴在哪里”及“另一半图案是怎样的”展开说明。

【设计说明：让学生应用对称的性质想象展开后的轴对称图形，进一步发展学生的空间观念。】

把课堂还给学生不能成为空头支票，需要教师舍得放权。本课通过“先立后破”“重组材料”，从有方格图辅助到舍弃方格图在白纸上画图，学生学习过程精彩，各种感受都很深刻，同时靠自己探索出了知识。

[ 参 考 文 献 ]

[1] 黄龙玲，邹立坝.“轴对称的再认识”教学实录与评析[J].小学数学教育，2021（Z3）：82-84.

[2] 杨灵君.怎样在轴对称图形教学中发展学生的空间想象能力[J].小学教学（数学版），2021（Z1）：143.

（責编 黄春香）