高中数学立体几何平面化思想的实践探究

周玉珍

(福建省南平第一中学 353000)

1 高中数学立体几何与平面几何的关联与对应

高中数学立体几何，是初中平面几何的延伸，二者同属几何学，知识方法具有关联性.平面几何培养学生的推理论证能力和代数化简能力，而立体几何培养学生的逻辑推理与空间想象能力.教师在立体几何中的教学方式，只有符合学生的认知发展规律，能够引导学生观察、类比、归纳，才能取得良好的教学效果.学生在立体几何中的学习方式，只有完善思维结构特征，能够将问题分析、迁移、转化，才能取得良好的学习效果.而学习立体几何，可以借助平面几何类比得到立体几何，或将立体几何转化得到平面几何，二者在教学与学习中既有统一性，又有关联性.作为平面几何的延伸，立体几何在知识、方法及思想上和平面几何是相呼应的，其本质是二维对三维的对应关系.

2 高中数学立体几何的平面化思想的定义

立体几何的平面化思想，即将空间中的点、线、面的关系，通过转化的思想，使之转化到某一个平面内，利用平面几何相关的知识、定理进行研究的思想方法.在解决问题时，抓住平面几何图形的特征，比如三角形的中位线原理，三角形全等原理，三角形的相似比关系，或者通过解三角形，得到题目所需的代数、几何关系，对于更为复杂的几何问题，应用转化与化归、函数与方程、数形结合等思想解决问题.

3 高中数学立体几何问题应用平面化思想的对策

3.1 平面抽离法

当几何体中的线与面的关系不明确时，可以将问题所涉及的局部平面抽离出空间，借助其平面图形更加直观的观察，并结合平面几何知识，得到需要的线线、线面或面面关系.以立体几何探究性问题为例：已知平面ABCD⊥平面AA1D1D，其中正方形AA1D1D棱长为1，矩形ABCD中，AB=2，点E是线段AB的中点，试问：线段AB上是否存在点P，使平面D1PC与平面PCD的夹角大小为60°？若存在，求出BP的长，若不存在，说明理由.

解题分析(1)立体几何问题平面化: 过点D1作D1H⊥PC，可证明得到PC⊥平面D1DH，从而证明得到DH⊥PC，说明∠D1HD即为平面D1PC与平面PCD的夹角；

(2)平面抽离：在立体几何中抽离出与未知量有关的平面图形，将知识化归为平面几何问题；

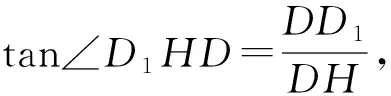
3.2 侧面展开法

常应用在立体几何的折叠问题中.通过对几何体的侧面进行展开，结合其侧面展开图研究问题，是平面化思想的重要手段与方法.通过化曲为直、化折为直，结合侧面，展开研究其平面与几何体的关联性，找到题目所需的的数量关系和位置关系，借助平面几何相关知识解决问题.以立体几何的折叠问题为例：在△ABC中，AD⊥BC，ED=2AE，过E作FG∥BC，且将△AFG沿FG折起，使∠A′ED=60°，求证：A′E⊥平面A′BC.

解题分析(1)几何体的侧面展开：借助展开后的平面图形，结合立体图形研究，抓住图形的两个关键：不变的线线关系，不变的数量关系；

(2)立体几何问题平面化：由平面图形的AD⊥BC，得到空间中的AE′⊥BC，在△A′ED中，构造余弦定理，计算得到A′D⊥A′E；根据线面垂直的判定定理推导证明，得到A′E⊥平面A′BC.

3.3 截面法

常用于立体几何的截面问题与球的切接问题.截面法大体分为两种，交线法与性质法.应用交线法作截面，作图关键在于确定截点，作图依据为基本事实；应用性质法作截面，作图关键在于找到平行的直线或平面，作图依据为线面平行、面面平行的性质定理.通过作出与未知量有关的截面图形，数形结合，产生与问题有关的平面几何关系，将立体几何问题平面化.

以立体几何的截面问题为例：正方体ABCD-A1B1C1D1的棱长为2，M、N分别是A1B1、A1D1的中点，过直线BD作平面α，使得平面α∥平面AMN，求平面α截该正方体的截面面积.

解题分析(1)性质法作截面：以C1D1，B1C1的中点P，Q为截点，连接PQ，B1D1，DP，BQ，NP，得到截线，根据面面平行的性质定理，作出满足条件(过直线BD，且与平面AMN平行)的截面DBQN；

(2)立体几何问题平面化：根据平面几何中梯形的定义，证明得到四边形DBQN为梯形，通过梯形的面积公式，计算得到截面DBQN的面积.

以外接球问题为例：三棱锥P-ABC中，△ABC为直角三角形，AB=AC=1，△PBC是正三角形，平面ABC⊥平面PBC，求三棱锥P-ABC的外接球的半径.

解题分析(1)交线法找球心：根据等腰直角三角形的性质，可知△ABC的外接圆圆心是BC的中点D，直线PD⊥平面ABC；根据正三角形的性质，可知△PBC的中心O为△PBC的外接圆圆心；过O作平面PBC的垂线l，找到球心也就是两垂线的交点O；

(2)立体几何问题平面化：根据外接球的定义，易得OB为三棱锥P-ABC的外接球半径，借助正三角形的性质和直角三角形的勾股定理，列出代数关系，计算得到球半径.

4 高中数学立体几何的平面化思想的实践难点

高中数学立体几何问题中，如何寻找关键的平面，如何转化为平面几何问题，是教师教学的难点，也是学生解题的难点，它的实质是利用几何相关的定义和性质定理将立体几何问题平面化，从思想上要注意空间与平面的相互转化.

5 高中数学立体几何的平面化思想的教学案例

5.1 高中数学必修第二册《立体几何初步》中应用平面化思想的教学实例

已知正方体ABCD-A1B1C1D1棱长为1，线段AD的中点为M，动点P在不含边界的正方形ABCD内运动，满足B1P∥平面A1BM，求线段C1P的最小值.

教学内容分析必修第二册《立体几何初步》中，处理立体几何的最值问题，需要将动态问题静态化，应用几何推理与代数推理相结合的办法实施.也就是找到动点在变化过程中的特殊的、确定的位置，借助平面几何的相关定理或进一步转化为函数、不等式问题来处理.

解题思路分析：根据面面平行的相关定理，推导得到动点P落在定直线DN上；关联平面几何的知识，代入点到直线的距离公式，或者构造勾股定理，计算点C1到直线DN的距离.

解题难点分析由线面平行的判定定理、面面平行的性质定理推导关系，构造截面，找到动点P所在的定直线的过程，是解题的难点.

平面化思想的应用分析：

(1)作出截面：由B1P//平面A1BM，转化得到过点B1的平面与平面A1BM平行，作出截面B1QDN，从而构造出与之相关的不变因素，即动点P在定直线DN上；

(2)动态问题静态化：动点P到定点C1的距离C1P，转化成定点C1到定直线DN的距离，当C1P⊥DN时，C1P取得最小值.根据三垂线定理，可证明底面上CP⊥DN，最终将问题转化成平面几何的最值问题；

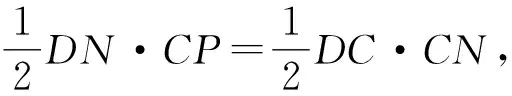
5.2 高中数学选择性必修第一册《空间向量与立体几何》中应用平面化思想的教学实例

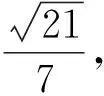
教学内容分析：选修第一册《空间向量与立体几何》中，空间向量法是解题的重要工具.解题的难点在于建系及写出坐标，对于较复杂的不能直接建系的几何体，将局部平面抽离出几何体，转化到该平面图形中研究坐标系及求解坐标.

解题思路分析：由面面垂直的性质定理，可以证明AC与CD、CE分别垂直.结合平面与平面的夹角公式，构造线线平行，根据线面平行的判定定理，推证得到CD//平面ABE；建立空间直角坐标系，求出所需的各点坐标，计算所需的方向向量，求得平面的法向量，利用空间向量中直线与平面的夹角公式，列出方程关系，计算未知数的值，代入得到点G的坐标，求出线段AG的长度.

解题难点分析(1)建系中的难点：根据面面垂直的性质，证明AC⊥平面CDE，可得AC为z轴，难点在于底面BCDE上要找到经过点C且互相垂直的两条直线；

(2)坐标化的难点：底面BCDE上各点的坐标，及线段AB上的点G的坐标的求解.

高中数学立体几何问题的平面化思想，即空间向平面转化、三维向二维转化的思想，是立体几何中最基本也是最重要的数学方法，贯穿着整个立体几何学习的始末.平面化的本质是应用平面化思想的对策,包括平面抽离法、侧面展开法、截面法，把空间中的元素转化到与已知条件和未知结论有关的平面中解决.应用平面化思想解题的过程中需要把握三个要点，一要弄清立体几何中线与面的位置、数量关系；二要找到三维中的几何元素对应的二维平面的几何元素；三是利用平面几何知识解决问题，构造已知元素与未知元素的代数关系式.立体几何问题的平面化思想，对突破空间障碍，对提高解题效率，灵活学习立体几何有巨大的帮助.