由2022年八省联考第8题引发的研究
李昌成
(新疆乌鲁木齐市第八中学 830002)
1 题目呈现
题目(2022年八省联考第8题) 设a,b都是正数,e为自然对数的底数,若aea+1+b A.ab>eB.b>ea+1C.ab 学生普遍反映本题无从下手,很难建立题设与问题间的关系.根据2021年全国高考乙卷第12题的结构、命题点位、解题方法,考生有大概的思路:构造,再利用单调性作答,但是很难具体实施解题思路. 解析由aea+1+b aea+1 ① 提取公因式,得aea+1 ② ③ ④ ⑤ ⑥ ⑦ 因为a,b都是正数, ⑧ ⑨ 本题还有其他构造方法,只是构造更加巧妙,对学生要求能力更高,尤其是等价转化的能力,抽象概括的能力! 另解1 设φ(x)=xlnx-x,则 φ′(x)=lnx+1-1=lnx. 由前文知b>e,所以φ′(x)>0. 所以φ(x)=xlnx-x在(e,+∞)上单调递增. 又φ(ea+1)=ea+1lnea+1-ea+1=(a+1)ea+1-ea+1=aea+1,由aea+1+b 所以φ(ea+1)<φ(b).所以b>ea+1. 另解2 设λ(x)=lnx+x(x>0), 则λ(x)在(0,+∞)上单调递增. 由aea+1+b 0 取自然对数,得 lnaea+1 化简,得lna+a+1 移项,得lna+a 所以λ(a)<λ(lnb-1). 因此a 解得b>ea+1. 关于构造思想,教材在不同章节均有一些思想渗透,我们要深入领悟.对导数而言,在人教A版选修2-2的第32页安排了以下经典证明习题: (1)ex>1+x(x≠0). (2)lnx 这两个习题给我们提供了学习构造法的平台,从代数的角度可以分别构造函数f(x)=ex-x-1(x≠0),h(x)=lnx-x(x>0),g(x)=x-ex(x>0),再利用这些函数的单调性证明不等式. 也可以依托函数y=ex,y=1+x,y=x,y=lnx,在同一直角坐标系中,通过图象直观感知不等式的正确性.事实上,基于这两个不等式结构和条件,我们可以构造大量的不等式,例如: (3)ex≥1+x((1)式扩大定义域). (4)ex-1>x(将(1)中x换成x-1). (6)2lnn (1)已知f′(x)g(x)+f(x)g′(x)>0,构造函数h(x)=f(x)g(x). (7)已知f′(x)+f(x)>0,构造函数h(x)=exf(x). (8)已知xf′(x)+f(x)>0,构造函数h(x)=xf(x). (9)已知xf′(x)+nf(x)>0,构造函数h(x)=xnf(x). 显然,以上条件不等式中不等号变为小于号,不影响函数构造. A.a C.b 于是f(0)=0,g(0)=0,h(0)=0,f(0.01)=a,g(0.01)=b,h(0.01)=c. 分别求导,得 所以g′(x) 结合导数的几何意义,得b 故选B. 例2 (2015年全国高考Ⅱ卷理科第12题)设函数f′(x)是奇函数f(x)(x∈R)的导函数,f(-1)=0,当x>0时,xf′(x)-f(x)<0,则使得f(x)>0成立的x的取值范围是( ). A.(-∞,-1)∪(0,1) B.(-1,0)∪(1,+∞) C.(-∞,-1)∪(-1,0) D.(0,1)∪(1,+∞) 因为当x>0时,xf′(x)-f(x)<0,故当x>0时,g′(x)<0. 所以g(x)在(0,+∞)单调递减. 又因为函数f(x)(x∈R)是奇函数, 故函数g(x)是偶函数. 所以g(x)在(-∞,0)上单调递减. 又g(-1)=g(1)=0, 当0 当x<-1时,g(x)<0,则f(x)>0. 综上所述,使得f(x)>0成立的x的取值范围是(-∞,-1)∪(0,1). 故选A.2 试题解答



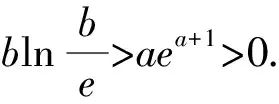



3 解答说明

4 追根溯源


5 常见构造模式





6 高考链接





