基于特征选择算法的个人信用预测模型

查志成，梁雪春

(南京工业大学 电气工程与控制科学学院，江苏 南京 211816)

0 引 言

随着互联网金融的飞速发展，个人信用数据的规模变得极其庞大。高维数据会使计算复杂度增加，训练效率低下[1]。特征选择算法通过选取优质特征，降低数据集特征维度，提高分类效率和准确率，且有去噪、防止过拟合的作用[2]。同时，降维后的模型具有更低的时间成本，也更容易被理解和解释[3]。

最初，学者们以实际数据为依托，通过算法进行智能筛选特征。张永梅等[4]通过mRMR算法来选择合适的特征，改善了XGBoost(extreme gradient boosting)的预测准确率。曾鸣等[5]通过卡方检验计算出每一个特征与类别的相关性，剔除无关的特征。近年来若干方法相互组合来筛选特征成为主流，陈谌等[6]提出了RFG-χ2来对特征进行选择，并应用在支持向量机上，得到最佳属性集且有很好的预测效果，但是没有考虑是否存在冗余特征。王名豪等[7]提出了RF-GBDT算法，得到的最优特征子集作为XGBoost的输入，分类效果比特征选择之前更佳，但是未考虑特征与标签之间的相关性。刘启川等[8]使用卡方检验和信息增益计算特征贡献度并设定阈值筛选特征，但是该算法没有结合搜索策略，选出更好的特征。

针对以上问题，本文提出了基于皮尔森相关系数和MI-GBDT的结合搜索策略的最优特征子集的选择方法，并将此算法应用于Lending Club平台公开的2016年～2020年的部分贷款数据上，为预测模型筛选出最优特征子集。

1 理论基础

1.1 皮尔森相关系数

皮尔森相关系数(Pearson correlation coefficient，PCC)是统计学3大相关系数之一，用于考察两变量之间的线性关联程度。对于两个随机变量X=(x1,x2,…,xn)，Y=(y1,y2,…,yn)， 样本的皮尔森相关系数如式(1)

(1)

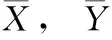
r的绝对值越大则两变量越相关；r的正负值表示两变量是正相关还是负相关；当r为0时表示两变量无相关性，当r为1或-1时表示两变量完全相关。

1.2 互信息理论

互信息(mutual information，MI)常被用来对特征间的相关性进行评价，是一种有效的信息度量方法[9]，它可以反映两变量之间的线性与非线性关系。设两个离散型随机变量X=(x1,x2,…,xn)，Y=(y1,y2,…,yn)， 且p(x,y)，p(x)，p(y) 分别为 (X,Y) 的联合分布函数，X的边缘分布函数，Y的边缘分布函数，则X，Y的互信息I(X;Y) 定义为

(2)

从式(2)可以看出，I(X;Y) 的意义是X，Y共享信息的一个度量，即如果知道其中一个变量，对另一个变量不确定度减少的程度。例如，若X,Y相互独立，那么知道X并不能对Y提供任何信息，则它们的互信息为0。

1.3 梯度提升决策树模型

梯度提升决策树(gradient boosting decision tree，GBDT)是由Friedman提出并改进的集成学习算法[10]，由多颗决策树组成，是梯度提升(Gradient Boosting)和决策树结合后的应用。GBDT中梯度提升采用了最速下降的近似方法来拟合回归树，用损失函数的负梯度近似表示Gra-dient Boosting中的残差，决策树采用了CART回归树。

设训练集S={(x1,y1),(x2,y2),…,(xN,yN)}， 损失函数为L， 最大迭代次数为T， 最终构造的强分类器为f(x)， 则GBDT的算法流程可描述为：

步骤1 初始化弱分类器

(3)

选取平方误差函数作为损失函数

(4)

步骤2 对迭代轮次t=1,2,…,T：

(1)计算样本n=1,2,…,N的负梯度rtn

(5)

(2)用 {(x1,rt1),(x2,rt2),…,(xN,rtN)} 拟合一个回归树，得到第t棵树的叶节点区域Rtj,j=1,2,…,J(J为叶子节点个数)；

(3)对j=1,2,…,J， 拟合出使损失函数达到最小的叶节点区域值，如式(6)

(6)

(4)更新强分类器

(7)

式中：I为示性函数。

步骤3 得到最终的回归树，如式(8)

(8)

2 模型建立

2.1 GBDT进行特征选择

利用GBDT进行特征选择属于特征选择中嵌入式方法。GBDT是生成回归树的过程，每个特征的重要度时可以根据该特征在分裂后，平方损失的减少值来衡量，减少的越多则该特征重要度越大，然后根据每个特征的重要度来进行特征的筛选。

对某一特征i，它的全局重要度可以通过它在每一棵树的单棵重要度的平均值来衡量，特征i全局重要度表达式如式(9)所示

(9)

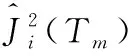
(10)

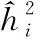
2.2 基于特征排序的搜索策略改进

在基于特征排序的特征选择算法中，对于已经按照重要度排好序后的特征集，选取前K个特征可以得到一个局部最优特征子集，然而前K个特征并不一定都对模型分类有帮助，K个特征之后的特征也有可能对分类效果有所提升，本文在此基础上对搜索策略进行改进，对K之前的某些特征进行删除，对K之后的某些特征进行添加，筛选出更优的特征子集，使分类性能进一步提高。改进后的搜索策略分为3个阶段：

第一阶段：对于按照某种评价准则降序排序后的特征，依次加入分类器中，模型的分类准确率一般会随着特征数量的增加呈现出先上升后下降的趋势，如图1所示，准确率达到最大时的特征数量记为K。

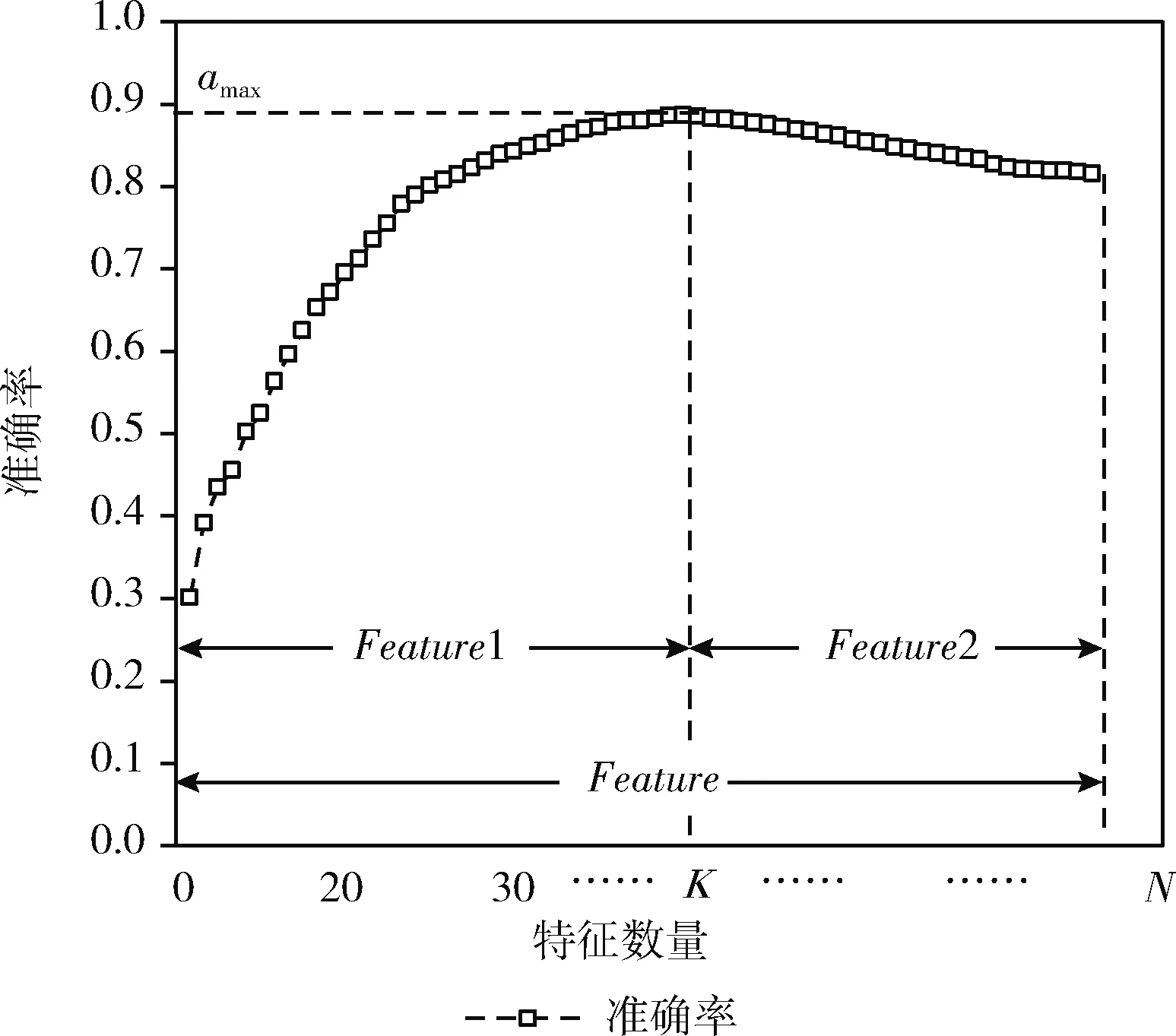
图1 准确率随特征数量变化

算法流程如下：

输入：排序后的特征集Feature={f1,f2,…,fN}

输出：K，最大准确率amax，

前K个特征集Feature1={f1,f2,…,fK},

剩余特征集Feature2={fK+1,fK+2,…,fN}。

Begin

(1) setF={} //设一个空集

(2) fori=1 toNdo

F=F+fi//向集合F中添加特征fi

ai=CAL_Acc(F) //计算特征子集F对应的数据在分类器下的准确率

(3)amax=max(a) //找出最大准确率

(4)K=argmax(a) //找出最大准确率对应的特征数量

(5)Feature1={f1,f2,…,fK}，Feature2={fK+1,fK+2,…,fN}

End

第二阶段：对于前K个特征组成的特征集合Feature1， 需要删除某些影响分类效果的特征。从后往前依次删除Feature1中的特征，每次删除后代入分类模型计算对应的准确率，若准确率未得到提升，则把该特征放回。算法流程如下：

输入：Feature1={f1,f2,…,fK}，amax

输出：删除一些特征后的特征集Feature1′

更新后的最大准确率amax

Begin

(1)Feature1′=Feature1

(2) Fori=Kto 1

Feature1′=Feature1′-fi

//减去集合Feature1′中的特征fi

atemp=CAL_Acc(Feature1′)

//计算特征子集Feature1′对应的数据在分类器下的准确率

if(atemp>amax)then

amax=atemp//若准确率提升， 则更新amax

else

Feature1′=Feature1′+fi

//若准确率未提升， 则添回删除的特征fi

End

第三阶段：对于K之后的特征集合Feature2， 需要筛选出某些能进一步提升分类效果的特征。从前往后依次将Feature2中的特征添加进Feature1′中，每次添加后代入分类模型计算对应的准确率，若准确率未得到提升，则把该特征删除。算法流程如下：

输入：Feature1′，amax，Feature2

输出：最终筛选出的特征集Feature3，amax

Begin

(1)Feature3=Feature1′

(2) Fori=K+1 toN

Feature3=Feature3+fi

//将Feature2中的特征fi加入Feature3中

atemp=CAL_Acc(Feature3)

//计算特征子集Feature3对应的数据在分类器下的准确率

if(atemp>amax)then

amax=atemp//若准确率提升， 则更新amax

else

Feature3=Feature3-fi

//若准确率未提升， 则删除添加的特征fi

End

2.3 皮尔森相关系数和MI-GBDT特征选择方法构建

图2 皮尔森相关系数和MI-GBDT 特征选择模型实现流程

步骤1 设训练集S={(xi,yi)|i=1,2,…,N}， 其中xi为特征向量，yi为标签变量，N为总样本数。特征集F={fi|i=1,2,…,m}， 其中m为特征维度。计算每个特征fi与标签之间的互信息值I,得到互信息值I的集合，I={Ii|i=1,2,…,m} 然后按照互信息值将特征由大到小排列，得到有序特征集合Order1={fi|i=1,2,…,m}。

步骤2 计算各个特征之间的皮尔森相关系数R={rij|i=1,2,…,m;j=1,2,…,m}, 其中rij表示特征i与特征j之间的皮尔森相关系数。然后根据Order1中的顺序，依次遍历里面的特征，并检查它的与其余特征的皮尔森相关系数是否有大于0.6的，若有，则删除互信息值小的那个，被删除的特征不再参与接下来的遍历过程。有序特征集合Order1删除冗余特征后的集合记为Order2。 此步骤是利用皮尔森相关系数去除冗余特征，算法流程如下：

输入：各个特征之间的皮尔森相关系数R={rij|i=1,2,…,m;j=1,2,…,m}， 有序特征集合Order1={fi|i=1,2,…,m}

输出：去除冗余特征后的有序特征集合Order2

Begin

(1)Order2=Order1

(2) fori=1 tom

forj=1 tom(j≠i)

if(rij≥0.6)

Order2=Order2-fj//删除冗余特征

End

步骤3 由于特征集发生了变化，所以重新计算剩余特征与标签特征之间的互信息值，并将其归一化，将互信息值I统一映射到[0,1]区间上，得到归一化后的互信息值Inrm={Inrmi|i=1,2,…,m}， 转换公式如式(11)

(11)

步骤4 计算每个特征的综合重要度ci, 并对特征按照综合重要度从大到小排列，得到有序特征集合记为Order3， 计算公式如式(12)

(12)

步骤5 对于排序后的特征，按照2.2节改进的搜索策略结合分类器进行特征选择，便可以得到最终的特征子集Order4和其分类准确率amax。

3 实验分析

3.1 实验数据及其预处理

为验证特征选择算法的有效性，本文选取了Lending Club平台官网上公开的2016年到2020年的199万条个人信用数据记录，数据包括了用户的基本信息、经济状况、信用状况和借款详情等，共144维，其中1个为标签特征。

首先要对数据进行预处理：

(1)标签特征处理。标签特征名称为loan_status(贷款状态)，共有8种取值：Current(进行中)、Issued(发出)、Fully Paid(全部偿还)、Charged Off(冲销，投资人有损失)、Default(违约)、In Grace Period(在宽限期)、Late (16～30 days)(延期16～30天)、Late(31～120 days)(延期31～120天)，将Charged Off作为好账处理，Default、Late(16～30 days)、Late(31～120 days)作为坏账处理，其余的无法判断状态，将对应的样本剔除。

(2)缺失值处理。对于缺失值大于15%的特征，将该特征删除；对于缺失值小于5%的特征，将对应的样本删除；对于其余缺失的数值型特征用平均值填补；对于其余缺失的类别型特征用众数填补。

(3)删除贷后变量。像out_prncp(剩余未还本金)、total_pymnt(已还金额)、recoveries(扣除费用后的总回收率)、last_credit_pull_d(信用证收回了这笔贷款的月份)等特征都属于贷后特征，会暴露标签信息，所以要删除。

(4)数据规范化。利用零-均值规范化(z-score)对特征进行规范化处理。

(5)字符串转换。对于一些原始类别中的取值为字符串的，采用标签编码把字符串转换成数字。

表1 预处理后的数据情况

3.2 特征选择

对处理完的数据进行特征选择，首先用式(2)计算72个特征(loan_status是标签特征不参与排序)与标签之间的互信息值，并按照从大到小进行排序，互信息值越大，说明与标签之间的关联度越大，重要度越高。

然后用式(1)计算各个特征(除标签特征)之间的皮尔森相关系数，得到以下的皮尔森相关系数图谱(取其中10个特征展示)，如图3所示。

图3 各特征之间的皮尔森相关系数图谱

从图3中可以看出有一些特征之间的相关系数比较高，属于冗余特征，应予以去除。所以根据2.3节中的去冗余特征算法，找出所有强相关特征(皮尔森相关系数绝对值大于0.6的)，删除其中互信息值低的特征。最终删除了29个冗余特征，除标标签特征外还有43个特征。

去冗余后的特征皮尔森相关系数图谱(取其中10个特征展示)如图4所示。

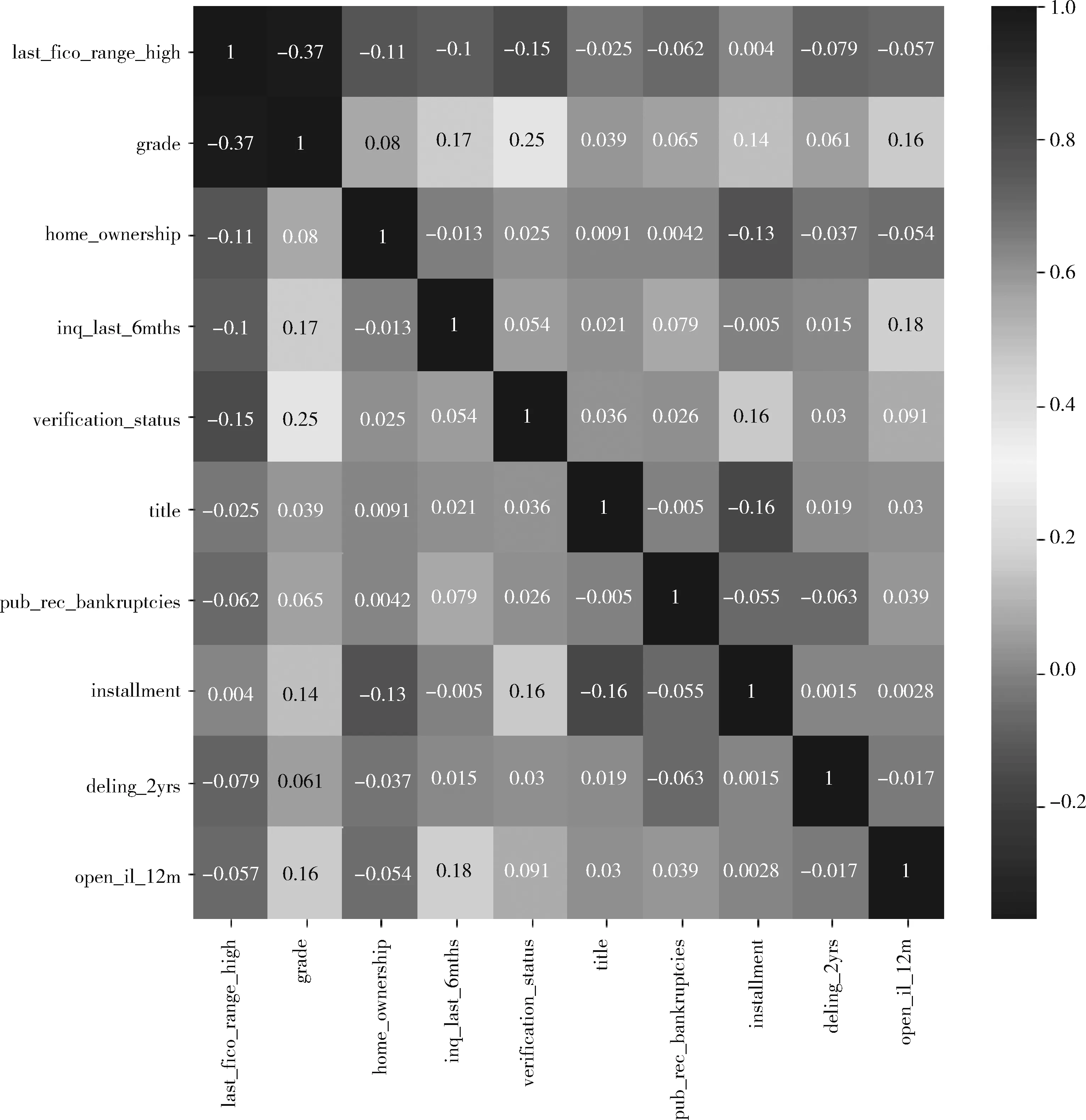
图4 去冗余后各特征之间的皮尔森相关系数图谱

从图4中可以看出，剩余的特征中不再含有强冗余的特征。

由于特征集发生了改变，现在需要重新计算各个特征与标签特征之间的互信息值，并进行归一化处理。接着利用式(9)计算各个特征的全局重要度，然后根据互信息值与全局重要度，用式(12)计算特征的综合重要度，并按照从大到小来排序，由于特征较多，取排名前十的特征展现出来，如表2所示。

得到特征的重要度排序之后，按照流程所描述的搜索策略对特征进行遍历。由于选择特征的时候需要用到分类器，不同的分类器最终得到的特征子集也是不同的，这取决

表2 特征综合重要度排序(前十位)

于最终的信用风险评估选取什么样的模型。现在分别选取决策树、支持向量机、朴素贝叶斯分类器进行实验。

实验结果见表3。

其中，当分类器选用决策树时，留下的4个特征分别为last_fico_range_high(借款人最近一次FICO所属于的上限范围)、grade(风险等级)、term(贷款期数)、application_typ(贷款是个人申请还是共同申请)。

表3 特征选择实验结果

当分类器选用支持向量机时，留下的5个特征分别为last_fico_range_high、grade、home_ownership(注册过程中提供的房屋所有权状态)、verification_status(总收入来源是否核实)、pub_rec_bankruptcies(公开记录破产数)。

当分类器选用朴素贝叶斯分类器时，留下的5个特征分别为last_fico_range_high、installment(若贷款产生，贷款人每月支付的款项)、term、emp_length(就业年限)、annual_inc(注册过程中提供的年收入)。

3.3 结果分析

为了验证本文提出的特征选择算法对模型分类的有效性，现在对测试集进行实验验证效果。将预处理后的数据集记为Original_data，去冗余特征后的数据集记为Selection1_data，经过MI-GBDT结合搜索策略选择特征后的数据集记为Selection2_data，用3种分类器针对不同特征子集下数据集实验，测试结果见表4。

表4 不同子集不同分类器下的模型性能比较

从表4中可以看出，使用PCC和MI-GBDT模型选择特征后，再用分类模型进行训练预测，分类性能有了显著的提高。

去冗余特征后的数据集Selection1_data对于原数据集，在决策树和朴素贝叶斯分类器下准确率略微有些下降，分别减少0.16%和0.9%，但是对不平衡数据集而言更有参考价值的AUC值分别上涨了0.001和0.015，训练时间也快了一倍。在支持向量机下，去冗余特征后的数据集的分类准确率比原数据集提升了15.7%，AUC值提升了0.039，训练时间更是提升了一倍。说明了基于皮尔森相关系数选择特征的有效性，在去除了冗余特征的同时，改善了分类效果，并且大大的减少了训练时间。

经过MI-GBDT结合搜索策略选择特征后的数据集Selection2_data对于原数据集Original_data和Selection1_data，效果提升则更为明显。在决策树下，准确率分别提高了4.33%和4.49%，AUC值分别提高了0.081和0.08。在朴素贝叶斯分类器下准确率分别提升了13.29%、14.19%，AUC值分别提高了0.015和0.052。在支持向量机下准确率分别提升了20.27%、4.57%，AUC值分别提高了0.046和0.007，时间更是提高了157.56 s和88.9 s。说明了MI-GBDT在去除完冗余特征的基础上，又进一步大幅提升了分类效果和模型训练时间。

将上述结果用3组柱状图来表示，可以更清晰展示本文特征选择算法对分类效果的提升，如图5和图6所示。

图5 不同特征子集在3种分类器下的准确率

图6 不同特征子集在3种分类器下的AUC值

4 结束语

本文提出了一种基于皮尔森相关系数和MI-GBDT的个人信用特征选择方法。针对个人信用指标存在冗余和无关指标的问题，根据皮尔森相关系数去除了冗余特征，利用互信息和GBDT分别从数据的信息相关性和分类能力两方面对特征的重要度进行度量，按照综合重要度大小对特征进行了排序，结合改进的搜索策略选出了最优特征子集。将此特征选择算法应用在3种传统分类器上，实验结果表明该算法筛选出的特征可以大幅提升分类器的分类效果，并且大大降低了数据的维度，提高模型的训练效率，使个人信用风险评估变得更加高效可靠。