D2D异构网络资源分配算法
段昌盛,孙 浩,魏 翔
(1.华中科技大学 电子信息与通信学院,湖北 武汉 430074;2.恩施职业技术学院 信息工程学院,湖北 恩施 445000;3.广西大学 商学院,广西 南宁 530004;4.云南国土资源职业学院 计算机系,云南 昆明 652501)
0 引 言
随着社会信息化、数字化的不断发展,人们对移动通信更高数据传输速率、更低网络延迟、更高能量效率以及更可靠的网络连接的需求不断增加,为满足社会对移动通信的巨大需求,第五代(5G)移动通信网络作为移动通信的关键技术需要进行重大的模式转换[1,2]。设备到设备(device to device,D2D)通信是5G移动通信的关键技术之一,通过运用蜂窝资源,使D2D用户设备(D2D user equipment,DUE)直接通信,无需接入点或基站的相互作用,减少基站的负载,提高通信系统的频谱效率及通信效率[3,4]。
基于能量收集的D2D异构通信网络是一种蜂窝网络[5,6]。其中,DUE从各种类型的能源中收集能量,将所获取的能量用于D2D通信,并以Underlay模式复用蜂窝用户设备(cellular user equipment,CUE)的频谱资源块[7,8]。在能量收集的D2D异构通信网络中,具有能量收集功能的用户设备可从周围的射频(radio frequency,RF)信号源中获取能量,但所收集能量的大小及持续时间与D2D链路的能量效率有关[9,10]。因此,能量收集技术的应用给D2D通信的资源分配带来了新的挑战。
为此,针对频谱效率、能量效率、网络延迟等不同目标的资源分配,众多专家学者针对D2D通信系统资源分配方法进行了大量的研究。文献[11]提出了一种基于链路状态预测的资源分配方法,提高D2D链路的总能量效率。文献[12]提出了一种基于社区网络的D2D资源分配框架,增强D2D资源共享,从而提升系统频谱效率。文献[13]提出了一种基于改进图着色的资源分配方法,用于降低信道复用所产生的干扰,提升系统吞吐量。但上述方法未考虑用户的能量收集功能,忽略了能量收集时间与D2D通信传输时间之间的最佳耦合关系。文献[14]提出了一种基于大规模认知蜂窝网络的能量传输模型和信号模型,以实现无线能量采集和安全的信息传输;文献[15]提出了一种新的蜂窝通信架构,可显著提高本地数据传输的频谱效率。但上述基于能量收集的D2D通信蜂窝网络中未考虑能量收集中的时隙分配、功率和资源联合分配等问题,实际应用效果不佳。
为此,针对D2D异构通信网络中的资源分配问题,提出了一种基于能量收集的D2D异构网络的资源分配方法(EH-DNH)。首先,基于系统模型提出了以最大化能量效率为目标的联合资源分配问题;通过等效变换将非凸优化问题转化为凸优化问题,并进行最优求解;其次,基于拉格朗日约束优化,提出了结合能量收集时隙分配、资源块和功率分配的迭代算法。最后,通过搭建仿真环境验证了所提方法的有效性。
1 系统模型与问题描述
1.1 系统模型构建
本文考虑一个下行链路EH-DHN场景,其中包含1个基站;C个下行链路蜂窝用户,表示为ω={1,2,…,C};D对D2D用户设备,表示为ψ={1,2,…,D}, 每对D2D用户设备都有一个DUE发送器(DUE_T)和一个DUE接收器(DUE_R)。如图1所示为系统模型结构。假设每个DUE都有能量收集功能,DUE发送器可以从周围的射频信号源中收集能量,将能量的收集过程建模为泊松过程。为便于建模,本文采用时隙机制,令EHi,k表示从时刻tk-1到时刻tk所收集的能量,并设置t0=0,tk=T。 令τk=tk-tk-1表示为时间间隔长度,tk和tk-1表示能量到达时刻,φ={1,2,…,K}, 则tk时刻的能量收集量EHi,k如式(1)所示
EHi,k~Poisson(λτk) ∀i∈ψ; ∀k∈φ
(1)
式中:λ表示平均每秒收集的能量。

图1 系统模型
为蜂窝网络中的每个CUE分配彼此正交的下行链路频谱资源块,并假设为CUE分配的频谱资源是预先确定的。令ρij,k∈{0,1}(i∈ψ,j∈ω,k∈φ) 表示第j个频谱资源块在第k个时隙中被第i个D2D链路的使用情况。假设CUE的每个下行频谱资源块最多可以由一个D2D链路共享,则其约束条件如式(2)所示
(2)

由此可得到,在第k个时隙中,为第j个资源块中的第i个D2D链路分配的数据传输速率如式(3)所示
(3)
式中:pij,k表示第k个时隙中第j个CUE资源块上第i个D2D对的发射功率,pj表示从基站到第j个CUE的发射功率,N0表示噪声功率。令Ri,k表示第k个时隙中第i个D2D对的数据传输速率,其数学表达如式(4)所示
(4)
令Pi,k表示第k个时隙中第i个D2D对的发射功率,其数学表达如式(5)所示
(5)
1.2 问题描述
在保证D2D链路能量收集约束和CUE服务质量的情况下,研究了能量收集时隙分配、频谱资源块与功率分配的联合优化问题,以实现对所有D2D链路平均能效的最大化。令EEi,k表示为第k个时隙中第i个D2D的能量效率,如式(6)所示
(6)
式中:Ps和ε为静态电路功率和功率放大器效率的倒数。则系统能效为所有D2D链路的平均能效,如式(7)所示
(7)
因此,可将D2D链路平均能量效率最大化的联合优化问题表示为如式(8)~式(13)所示
(8)
(9)
(10)
(11)
(12)
ρij,k∈{0,1}pij,k≥0 0≤tij,k≤τkpj≥0 ∀i∈ψ;j∈ω;k∈φ
(13)
其中,EHi,k表示从时刻tk-1到时刻tk收集的能量;τk表示连续两个到达的能量之间的时间间隔;Rj表示每个CUE的最小传输速率。其中,式(9)表示每个D2D链路仅可以重复使用CUE的其中一个资源块,且每个资源块最多能被一个D2D链路重复使用;式(10)表示能量约束,表明系统所消耗的能量总量必须小于等于初始能量与所收集的能量之和;式(11)定义了能量传输持续时间的约束条件,表明D2D传输的持续时间不能大于时隙长度;式(12)定义了CUE的QoS约束,表明每个CUE的数据传输速率必须大于最小传输速率。
2 联合优化算法
2.1 问题等效转换
由于pij,k,tij,k和pj是连续变量,而ρij,k是二进制变量,因此式(8)~式(13)所提资源分配优化问题,是一个结合了非凸目标函数和QoS约束的混合整数非线性规划问题,难以直接求解。为解决这一非凸优化问题,利用函数来描述CUE链路的传输功率。类似于文献[16],为了解决这个非凸优化问题。假设第j个CUE的资源块被第i个D2D在第k个时隙中重复使用,即ρij,k=1。 由式(12)计算得到如式(14)所示方程
(14)
式中:α=2Rj-1。

(15)
(16)
(17)
(18)
(19)
由式(16)~式(19)可知,进行等效变换后,新的优化问题的优化变量已减少为l={ρij,k,pij,k,tij,k}。
此时,最佳能量效率EE*的数学表达如式(20)所示
(20)
由此可知,最大化系统能效的充要条件是每个D2D对的能效都必须是最优的。因此,可将优化目标函数重写为式(21)所示方程
(21)

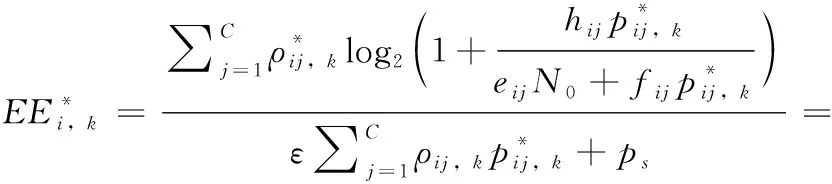
(22)

(23)
(24)
根据非线性分数规划理论,可将优化问题转换为相应的减法形式,如式(25)所示

(25)

同时,根据非线性分数规划理论和最大化系统能效的充要条件,还可将优化问题转换为如式(26)所示方程

(26)
转换后的等效优化问题可表示为如式(27)~式(30)所示

(27)
(28)
(29)
(30)

为此,本文将ρij,k取值范围放宽到[0,1]区间,同时引入变量xij,k=ρij,kpij,k。 将式(27)~式(30)所示问题转换为易于处理的优化形式,并用 (xij,k/ρij,k) 替换pij,k, 得到如式(31)~式(34)所示

(31)
(32)
(33)
(34)
此时,变换后的优化问题的目标函数在 (ρij,k,pij) 中是凸的。此外,该优化问题中的所有约束在ρij,k和xij,k中均为凸的。因此,变换后的优化问题是凸优化问题,可根据卡罗需-库恩-塔克(Karush-Kuhn-Tucker,KKT)条件进行最优求解。
2.2 优化迭代算法
通过放宽式(27)~式(30)的约束条件,将拉格朗日函数定义为式(35)所示

(35)
式中:λ1,j,k≥0,λ2,i,k≥0,λ3,i,k≥0, 分别为式(28)、式(29)、式(30)约束条件对应的拉格朗日乘数。由此进一步得到对偶函数,如式(36)所示

(36)
式中:γ=(λ1,j,k,λ2,i,k,λ3,i,k),l={ρij,k,pij,k,tij,k}。

(37)

(38)
进一步分析可知,式(36)对偶函数可解耦为C个独立的子问题,则第j个频谱资源块对应于的子问题可表示为如式(39)所示
(39)
式中:lj={ρj,k,pj,k,tj,k}。 令ρj,k,pj,k和tj,k分别表示在第k个时隙中第j个频谱资源块处的ρ,p,t的第j列。
由于式(28)的约束,可将单个频谱资源分配给一个D2D链路,且频谱资源块指示符ρj,k除了有一个二进制非零项外,为一个全零矩阵。因此,可通过计算得的最优值,如式(40)所示
(40)
式中:ηi,j,k如式(41)所示
(41)
因此,由式(40)可知,第k个时隙中的第j个频谱资源可分配给第i个D2D对,此时的ηi,j,k值最高。同时,根据式(41)可知,ηi,j,k取决于不同的信道增益。因此,可以从暂时放宽的约束条件中获得整数解。
3 仿真结果与分析
3.1 参数设置


表1 仿真参数
由于能量收集过程是呈现泊松分布的,在到达tk时刻的速率为λ=3 mJ/s,则收集的能量在[0,100] mJ之间呈均匀分布。在仿真中,为每个配置进行300次独立运行,取其平均值作为最终结果。
在此次仿真中,将对所提资源分配方法与以下方案进行对比分析:
(1)基于时隙分配、资源块和功率分配的优化方法(STRP):该方法是在保证能量收集约束和CUE服务质量的情况下,将所有D2D链路的频谱效率最大化。
(2)基于能量收集时间和传输时间的优化方法 (ETRP-E):该方法的主要目的是将能量收集时间等于以能量效率为目标的传输时间。
(3)基于能量收集时间和传输时间相等的资源分配优化方法(STRP-E):该方法中,令第k个时隙的第i个D2D链路的频谱资源块传输时间和能量收集时间等于τk/2, 从而提高频谱效率。
(4)基于D2D通信的联合节能资源分配和功率控制方法(JRAPC):该方法的主要目标是使每个DUE在使用电池电源时都具有相同的初始能量,从而最大程度地提高所有D2D链路的平均能效。
3.2 不同参数下的能效仿真分析
如图2所示,分别为QoS约束下,在不同CUE数量下,当Rj=12 bits/s/Hz和Rj=16 bits/s/Hz时的系统平均能效。由图可知,除JRAPC方法外,系统平均能效随CUE数量的增加而增加。其主要原因是,在JRAPC方法中,带有电池供电的CUE没有能量收集功能,其传输时间tij、kis等于τk。因此,CUE的可用能量随时隙的增加而减少。同样,带有电池电源的DUE在JRAPC方法中也没有能量收集功能,其传输时间tij,k等于τk。因此,DUE的可用能量也会随着时隙的增加而减少。
同时,由图2可知,所提ETRP方法和ETRP-E方法可获得比STRP、STRP-E和JRAPC方法更高的能量效率。这是因为通过ETRP方法目标函数解决的优化问题是平均能量效率最大化,但通过STRP方法处理的优化问题是使频谱效率最大化。由于ETRP可获得最佳能量收集时间(是ETRP-E能量收集时间τk/2的二分之一),因此ETRP可获得比ETRP-E更高的能量效率。同理,STRP方法也可获得比STRP-E更高的能量效率。
此外,由图2可知,QoS约束越低,系统所获取的平均能量效率越高,主要因为pj随Rj的增加而增加,而EE随着pj的增加而减小。

图2 不同CUE数量的平均能效

图3 不同QoS阈值的能量效率
如图3所示,为不同QoS阈值、不同CUE数量下系统的平均能源效率。其中,CUE的数量分别为C=10和C=6。由图可知,所提ETRP和ETRP-E方法可获得比STRP、STRP-E和JRAPC方法更高的能量效率。为满足更高的QoS阈值要求,Rj从基站到第j个CUE的传输功率需求将更高,因此系统的平均能量效率将随QoS阈值的降低而降低。由此可知,ETRP在降低QoS阈值的情况下,可达到比ETRP-E更高的能量效率,但ETRP的相对优势将随着QoS阈值的降低而降低。因为当QoS阈值较高时,从基站到第j个CUE的传输功率将较高。同理,在相同的情况下,STRP也可以达到比STRP-E更高的能量效率。
同时,由于频谱资源块的数量等于系统模型的CUE数量,因此由图4、图5可知,系统可通过更大的CUE数量获得更高的平均能量效率。其中,由于JRAPC方法无法实现能量收集,因此与ETRP、ETRP-E、STRP和STRP-E方法相比,JRAPC方法的能量效率最低。
如图4所示,分别为能量到达率λ=6 mJ/s和λ=3 mJ/s时,不同D2D对距离下的系统平均能量效率。由图可知,所提出ETRP和ETRP-E方法的能量效率均高于STRP、STRP-E和JRAPC方法。同时,由于第j个资源块上第i个D2D链路的发送器和接收器之间的信道增益随D2D对距离的增加而减小,而平均能量效率随信道增益的减小而减小,因此系统平均能量效率随D2D对距离的增加而减小。此外,由图可知,ETRP方法获得的能量效率始终高于ETRP-E,主要因为ETRP方法可获得最佳的能量收集时间。同理,STRP的能量效率也高于STRP-E。
综上,由于所提方法在每个时隙中可获得更多的能量,其能量到达率就越高,因此所提方法可在更大的能量到达率(λ=6 mJ/s)下获得更高的平均能量效率。
如图5所示,为当D2D对距离分别为20 m和30 m时,不同的基站和CUE距离下系统的平均能效。由图可知,所提ETRP和ETRP-E方法的能量效率均高于STRP、STRP-E和JRAPC方法,且系统平均能量效率随基站和CUE之间的距离增加而降低。其主要原因是基站与第j个CUE之间的传输信道增益gj,随基站与CUE之间距离的增加而减小。为满足QoS约束,系统需要较高的传输功率pj和较低的传输信道增益gj。因此,当pj较高时,其获得的能量效率则较低。在不同的基站和CUE距离下,ETRP方法所能达到的能量效率总是高于ETRP-E方法。此外,当基站和CUE之间的距离达到150 m时,STRP和STRP-E方法的能量效率非常低,且接近于零。综上,所提方法可在较短的D2D对距离(20 m)情况下,获得较高的平均能量效率。

图4 不同D2D对距离的平均能效
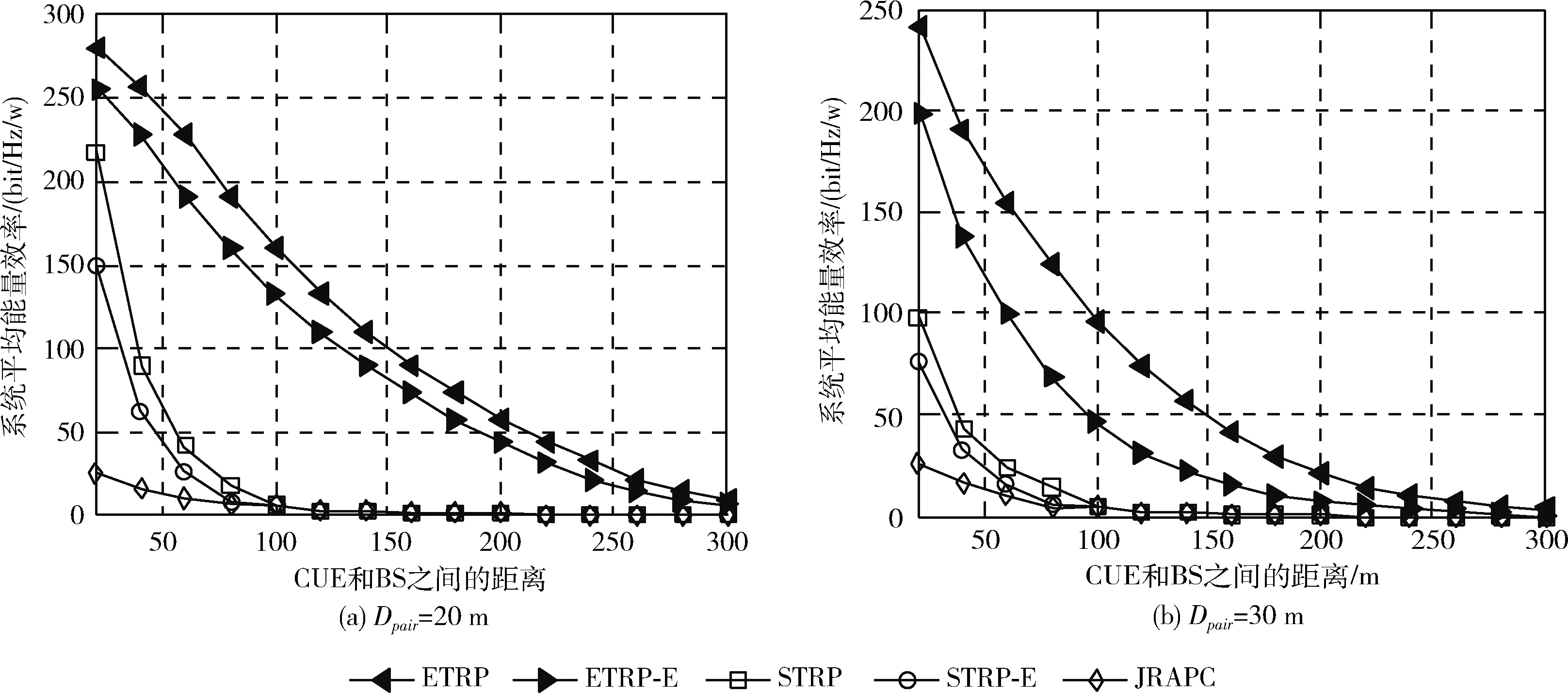
图5 不同BS和CUE距离的平均能效

图6 不同能量到达率下的平均能量效率
如图6所示,为当基站和CUE之间的距离分别为60 m和80 m时,不同能量到达率下的系统平均能量效率。由图可知,所提ETRP和ETRP-E方法可获得比STRP和STRP-E方法更高的能量效率,且系统平均能量效率随能量到达率λ的增加而增加。其主要原因是在每个时隙中,所提方法能够获得更多的能量,因此其能量到达率更高。同时,由于ETRP可获得最佳的能量收集时间,ETRP总能达到比ETRP-E更高的能量效率,且能够随着λ的增加而增加。
4 结束语
针对D2D异构通信网络中的资源分配问题,提出了一种基于能量收集的D2D异构网络高效资源分配方法,并通过仿真计算得出以下结论:
(1)所提方法通过等效变换将非凸优化问题转换为凸优化问题,能够有效保证在每个D2D链路的能量效率最大化。
(2)与ETRP-E、STRP、STRP-E和JRAPC几种方法相比,所提方法在不同的网络参数设置下均能达到更高的能量到达率,从而实现更高的能量效率。
(3)本文研究中,尚未考虑CUE的每个下行链路频谱资源块在多个D2D链路共享下的场景,后续研究中将继续针对该问题研究能量到达过程的复杂建模方法,以及不同目标DUE的模式场景。

