基于隐马尔可夫的机械臂浅深度插入控制策略*

贺道坤

(南京信息职业技术学院 智能制造学院,江苏 南京 210023)

0 引 言

在我国的工业生产领域中,有关机械零件的装配还有一部分要依靠人工来完成。近年来,随着机械领域的快速发展以及制造业的业务拓展需求,自动化装配成为主流,机械臂装配也一直是机械领域研究的前沿[1-3]。

人工装配存在着装配精度差、效率低及成本高等缺点,使得借助机械臂的自动装配技术得到了人们的重视,其自身也得到了快速发展[4-6]。

其中,有一种机械臂装配应用场景,被称之为“轴孔装配(peg-in-hole assembly)[7,8]”。轴孔装配是目前工业生产中常见的作业形式,广泛出现在汽车、轨道交通、飞行器等领域的机械系统制造装配中。

通过自动化轴孔装配可以在最小化零件数量种类的同时,最大限度地提高零件的夹持性和插入性,从而极大地提高装配的效率,缩短机械产品的生产周期,这已成为轴孔装配的主流解决方案[9]。

在该研究领域,国内现在已有大量的研究成果。朱博文等人[10]详细阐述了机械零件自动轴孔装配的种类和发展现状,分析了装配系统中所应用的关键技术,并且指出,当前自动轴孔装配技术存在搜寻过程的周期不确定性强、搜寻效率较低等不足。为了保证机器人在任意的抓取位姿都能够完成3种形状轴孔零件的装配任务,刘少军等人[11]提出了一种利用力传感器实现主从双臂协调运动的轴孔装配策略,但该策略受到传感器性能的约束。针对工业机器人自动装配效率低、环境适应性差等问题,潘柏松等人[12]提出了一种基于几何约束物理模型与隐马尔可夫链模型相结合的机器人轴孔装配策略,但对于高精度、小间隙轴孔零件,采用该装配策略时,其加工误差对于机器人轴孔自动装配系统的影响较为明显。

在该领域,国外也有不少研究成果。NGUYEN H T等人[13,14]结合角动量守恒定律,提出了一种基于RNS的翻滚目标机械臂装配算法,但对于拥有6自由度的机械臂而言,该算法的应用范围受到很大的限制。HOGAN F R等人[15]提出了一种基于数据驱动的机械臂装配模型,从而避免了直接从大量的原始数据中学习重复的抓取策略;然而，该模型需要根据当前装配构型的预测值不断地调整接触点,因此是一个动态的装配过程。与之类似,CALANDRA R等人[16]提出了一种端到端的装配模型,以预测当前装配下的最优策略,但也存在适用场景受限的不足。

在轴孔装配方面,由于其重力所产生的扰动力与插装力在同一轴线上,插装过程容易控制,从技术上来考虑,这种装配方式难度相对较小。水平方向装配是一种较为新颖的装配方式,由于其重力产生的扰动力与装配力方向垂直,在插装的过程中容易晃动,装配难度相对较大。

然而,还有一类将垂直控制与水平控制相结合的装配方式,对于机械臂而言,其控制策略更难以掌握。其中之一是被称之为“浅深度插入(shallow-depth insertion)”的机械臂装配方式,指的是通过机械臂将相对较小较薄的零部件插入相对较浅的凹槽中。在灵巧性以及抓取方式上,与通常的机械臂轴孔装配相比,这种应用场景有着很大的不同。

在传统的轴孔装配中,机械臂抓住部件侧面,并与相对较深的孔壁接触。然而,对于浅深度插入装配任务,机械臂如再采取这种握持方式,则对于较小、较薄部件就可能抓不稳,甚至不能侧握。

在机械臂装配任务中,由于被操纵的对象会与环境接触,力控制技术是必要的,装配运动需要设计合适的力控参数。对于简单的装配任务,如轴孔装配任务,可以采用固定的力控制参数,或采用试错方式获得力控制参数来加以实现。然而,对于浅深度插入这类更为复杂的装配任务,则必须根据任务状态对力控制参数进行调整。

为此,为得到适用于机械臂浅深度插入的控制策略,笔者提出一种基于隐马尔可夫的浅深度插入控制策略,即通过采集人工操作数据,获得浅深度插入力控参数,利用阻尼控制律对人工操作过程进行建模,发挥隐马尔可夫处理多时间序列的关联优势,对力控参数的时间序列数据进行建模,得到用于机械臂浅深度插入的控制策略。

1 基于人工操作数据的浅深度插入策略

1.1 浅深度插入操作分析

此处以干电池插入为例进行具体说明。

对于机械臂来说,将圆柱形操纵对象插入装有弹簧盒中的这类浅深度插入操作是一项常见但复杂的装配任务,需要机械臂根据反作用力和物体的构型来控制整个装配运动。

浅深度插入示例如图1所示。

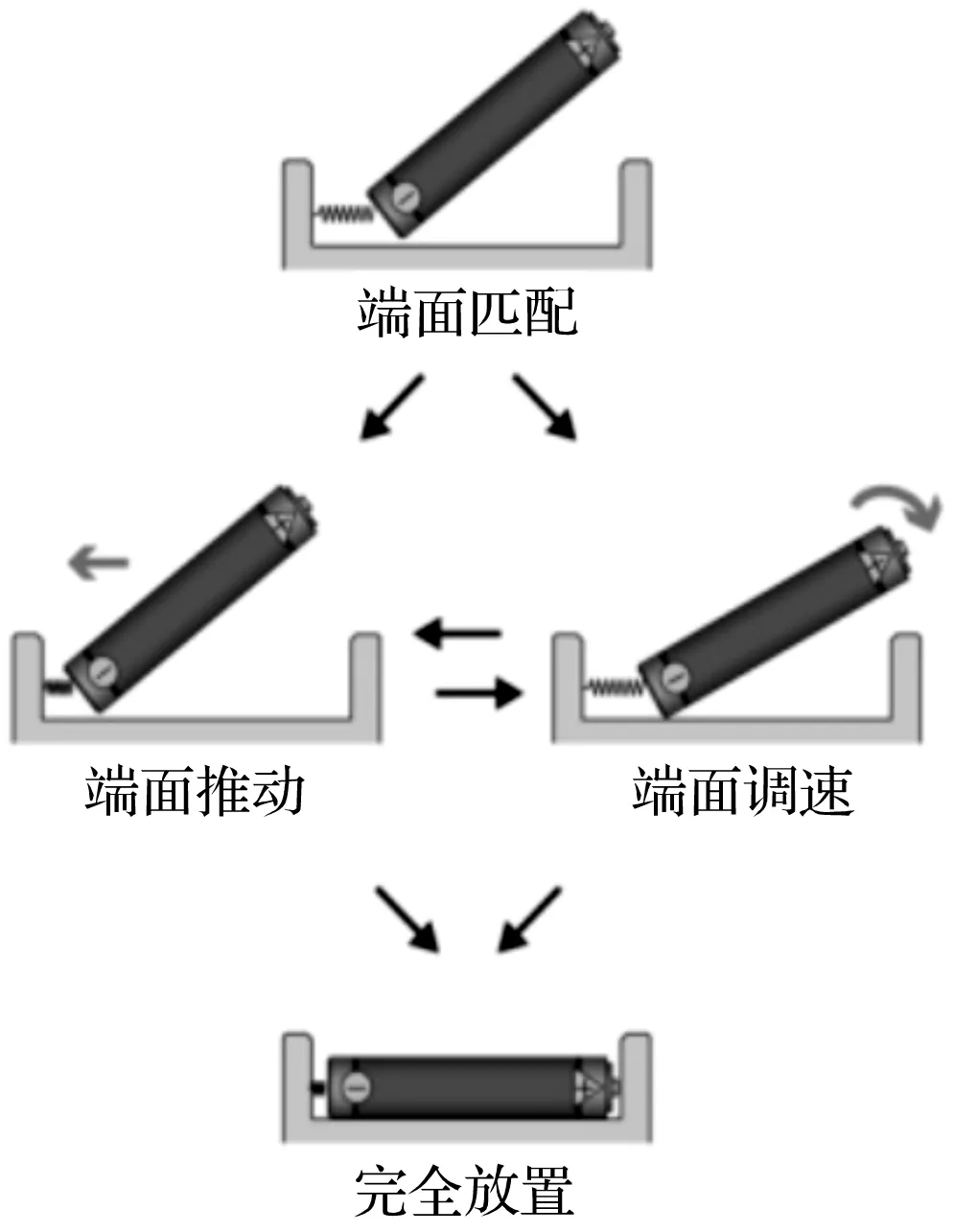
图1 浅深度插入示例

上述浅深度插入操作可分为以下基本动作:

(1)电池与被接触对象的端面匹配;(2)电池向端面的推动运动;(3)用于被接触对象方向的旋转运动;(4)电池与被接触对象的完全放置。

1.2 人工操作数据获取分析

对于机械臂而言,浅深度插入控制是一项复杂的装配任务,在装配过程中需要进行一些力控参数的切换。对于人工操作而言,浅深度插入控制却可以轻而易举地完成。

从策略上来看,机械臂浅深度插入控制技术可以很好地借鉴人工操作的控制策略,进一步降低机械臂的操控难度。其具体步骤如下:

首先,笔者利用代表机械臂的实验装置获得人工操作数据,并确保所获得的装配策略能够应用于机械臂(操作员的动作必须像机械臂一样受到限制,人工操作数据应该包括被操纵物体的位置和物体与环境之间的反作用力);

然后,基于实测的人工操作数据,笔者识别演示中力控参数的时序数据,对所获得的力控制参数的时序数据进行建模,并将其划分为一些控制策略,确保能够将这些策略有效应用于机械臂;

最后,采用隐马尔可夫进行建模(隐马尔可夫是一种可用于建模和随机数据分析的统计框架[17]),这样不仅可以描述可观察的随机过程,而且可以描述数据背后的不可测过程;通过对隐马尔科夫模型进行分析,从而构建机械臂浅深度插入控制策略。

1.3 人工操作数据获取过程

浅深度插入示例如图2所示。

图2 人工操作数据采集设备

图2中的人工操作数据是使用一个模拟机械臂的设备来进行测量的,该设备中间部分装有6自由度的力传感器(包括力传感器设备重量为0.5 kg,这让人工操作者可以轻松地进行操控)设备的末端装有代表干电池的圆柱体部件(其尺寸与电池相同,即直径1.4 cm,长度5 cm)。

人工操作数据采集过程示例如图3所示。

图3 人工操作数据采集过程示例

为全面获取人工操作数据,操作者运用设备重复40次浅深度插入动作,每10次试验中有短暂的休息时间。其间,操作者用高速摄像机拍摄,根据直接线性变换(direct linear transformation,DLT)方法[18],使用空间位置测量系统实时标记贴附在设备手柄上的重心位置,并通过标记的位置计算设备的位置和方向;电池部件与卡槽之间的反作用力由设备中的力传感器测量;对位置测量和力测量的采样频率分别为240 Hz和1 kHz。

测量的人工操作数据情况如图4所示。

由图4可知:期初2 s～2.3 s左右,设备处于搜索运动阶段;随后,由于沿弹簧方向(y轴)的反作用力fy的增大,设备沿y轴的位置减小,开始对弹簧压缩的推动;从大约2.8 s开始,设备绕x轴方向角rx逐渐减小,而绕同一轴的力矩绝对值mx增大,旋转运动在3.2 s～3.8 s间完成,其力矩出现多次波动。

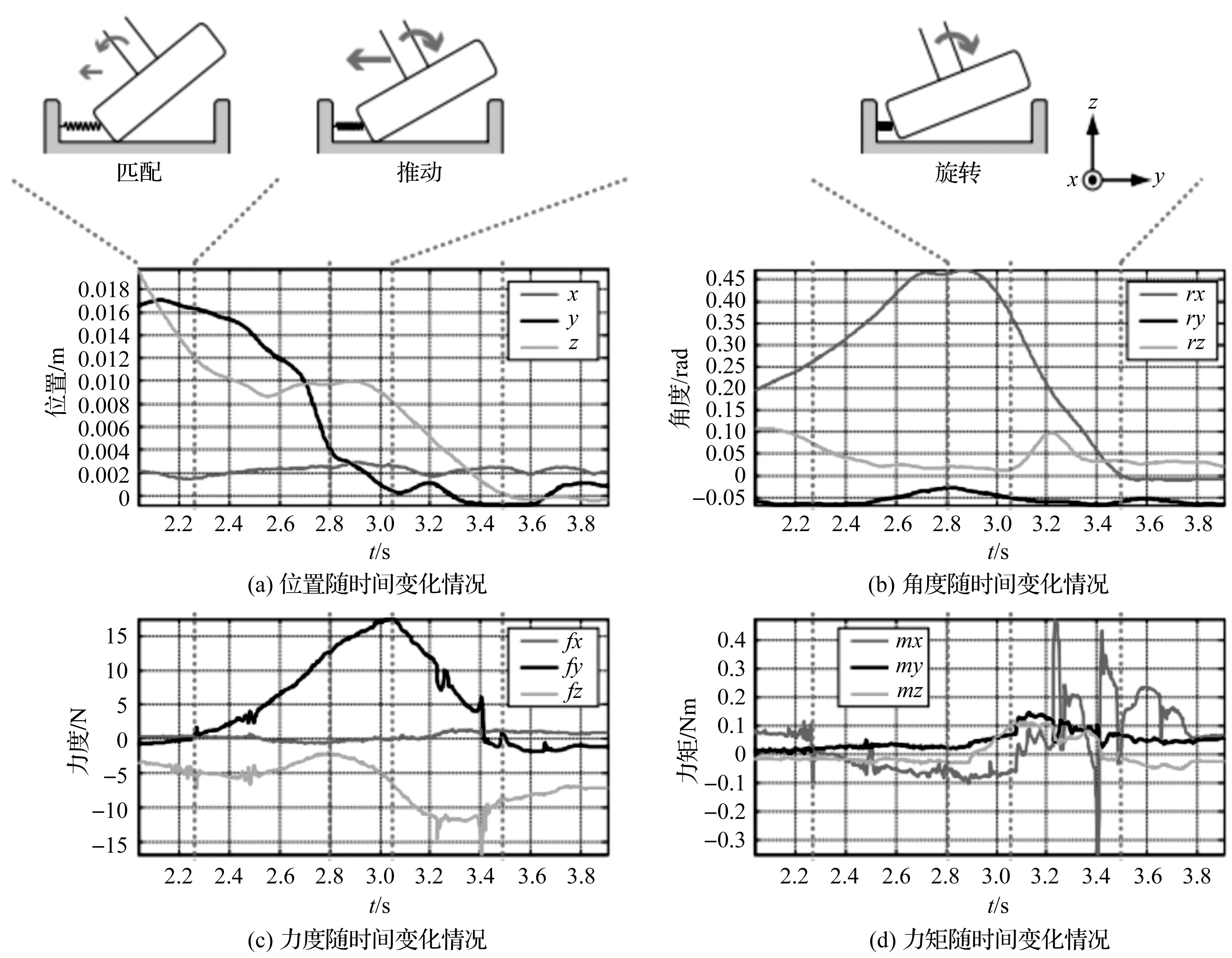
图4 测量的人工操作数据情况x,y,z—空间坐标轴方向,m;rx—x轴方向角,rad;ry—y轴方向角,rad;rz—z轴方向角,rad;fx—x轴方向作用力,N;fy—y轴方向作用力,N;fz—z轴方向作用力,N;mx—绕x轴的力矩,Nm;my—绕y轴的力矩,Nm;mz—绕z轴的力矩,Nm

2 人工操作过程的阻尼控制律模型

在接下来的步骤中,笔者根据测量到的人工操作数据,在每个采样时间里估计人工操作员使用的力度控制参数。

由于机械臂操控需要综合考虑控制力与作用于物体上反作用力对机械臂速度的影响,笔者采用符合实际的阻尼控制律对人工操作过程进行建模,即将人工操作过程等效为机械臂,将其运动速度分解为自用运动速度以及反作用力速度。

阻尼控制律模型如下:

vref=v0+Afout

(1)

式中:vref—应用于机械臂的参考速度,m/s;v0—标称速度,m/s;A—通道矩阵;fout—作用于物体上的反作用力,N。

标称速度和通道矩阵均被视为阻尼控制参数,并由它们确定机械臂运动。此外,通道矩阵还决定了应如何根据反作用力对参考速度进行修正,标称速度则描述了自由空间运动。

简便起见,笔者假定通道矩阵A为对角矩阵,并对通道矩阵采用约束条件ai,j≥0(i,j=x,y,z,rx,ry,rz),以此来对相关参数进行估计。

为了更好地模拟人工演示动作,笔者关于p轴(p=x,y,z,rx,ry,rz)将式(1)改写为:

(2)

式中:xp—设备模块沿p轴或绕p轴所测量的位置信息,m;Ap—通道矩阵A沿或绕p轴的行向量,且Ap=[ap,x,ap,y,…,ap,ry,ap,rz];带有k的值—t=kΔ时的实测数据,其中:Δ—采样周期;θp—需要估计的参数。

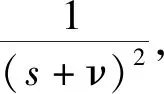
双线性z变换模型式为:

(3)

(4)

其中:

Xp(k)=T1(z)xp(k)

(5)

F(k)=T0(z)f(k)

(6)

(7)

(8)

笔者利用带遗忘因子的递归加权最小二乘(weighted least squares,WLS),对推导出的离散时间模型进行更新,可得到如下更新模型:

(9)

其中:

(10)

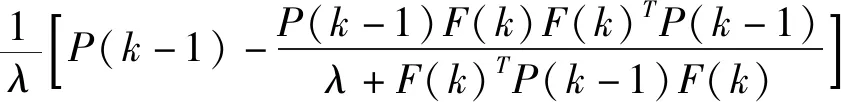
(11)

(12)

式中:Cp—一个只有0或1的矩阵;O0—一个零矩阵。

利用拉格朗日待定乘子求解该约束最小二乘问题,得到如下更新模型:

(13)

3 隐马尔可夫建模

笔者通过识别人工操作数据,获得阻尼控制参数的时间序列数据,并基于隐马尔可夫(hidden Markov model,HMM)对机械臂浅深度插入控制进行定量建模。笔者采用连续参数隐马尔可夫模型来避免控制行为输出符号的量化误差。

3.1 隐马尔可夫过程参数

事实上,隐马尔可夫过程是随机跃迁连接有限状态的集合。连续参数隐马尔可夫通常有以下5个参数:

(1)状态S=S{si}(i=1,2,…,N)。其中:N—设计者初步确定的状态数;

(2)输出符号O={ok}(k=1,2,…,∞)。通常为隐马尔可夫过程的可观测数据;

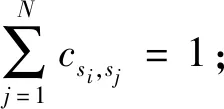
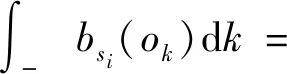
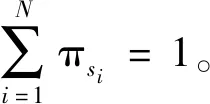
3.2 隐马尔可夫信号输出

对于浅深度插入的信号输出而言,由于机械臂浅深度插入几乎可以用y-z平面来描述,所以其输出y的矢量模型为:

(14)

其中:

x′=[yzrx]T

(15)

(16)

(17)

此外,符号的输出概率可由多维高斯分布定义为:

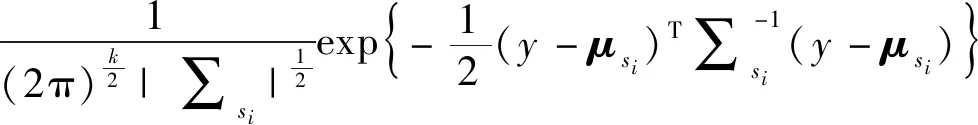
(18)

式中:k—输出信号向量的维数,且k=12;μsi—均值向量,μsi∈Rk;∑si—协方差矩阵,∑si∈Rk×k,为了便于机械臂的实现,假设其为对角矩阵。

3.3 隐马尔可夫拓扑结构

在机械臂浅深度插入过程中,由于笔者选择了控制策略组合来实现装配任务,在其任务完成过程中,其控制策略在某些时间段要重复使用。

对于随机变化的控制策略,由于其具有相当大的动态适应性,隐马尔可夫模型(HMM)在揭示多个时间序列之间的关联关系方面具有显著优势,能够有效评估人类与机械臂操作的相似性。

因此,笔者采用遍历模型来表示隐马尔可夫的状态连接,并针对隐马尔可夫拓扑结构的确定与参数估计,笔者利用MATLAB的隐马尔可夫工具箱,根据辨识出的阻尼控制参数序列,对隐马尔可夫参数进行估计。

其中,状态数按估计协方差矩阵的值来确定,其评估值由以下模型确定:

(19)

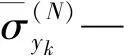
3.4 隐马尔科夫状态转移

隐马尔科夫状态转移过程如图5所示。

图5 隐马尔科夫状态转移过程示图

为了掌握机械臂浅深度插入所需的装配策略,笔者对上述隐马尔科夫模型进行分析。

在图5中,笔者根据估计的初始状态概率π和状态转移概率C,描述了机械臂浅深度插入隐马尔科夫的状态转移过程。总体而言,隐马尔科夫的状态连接过程形成了一个从左至右的串行流程,即机械臂浅深度插入可以通过一些串联的控制策略来实现。

其中,每个状态下执行的控制策略为:

(1)初始状态s1。人工操作在该状态下进行电池端面与v0和A较小的弹簧匹配运动,整体过程缓慢;

(2)过程状态s2。与s1相比,ω0x的平均值增大而arx减小。这一过程主要执行刚性旋转运动;此外由于y增加和fy减少,在推动前将实现“电池”方位的微调;

(3)过程状态s3。在此状态下,沿弹簧方向的反作用力fy以及ω0x将增大,而ay将减少;

(4)过程状态s4。与状态s3相似,fy和ω0x逐渐增加,而ay逐渐减少。此外,v0y将大大降低。在这一状态下机械臂将继续推进;

(5)过程状态s5。这一状态中虽然v0y继续减小,但ay将增至最大;

(6)过程状态s6。围绕旋转轴,该状态保持与状态s5相同的控制策略。在弹簧方向上,由于v0y逐渐增加,y保持较大的值,并进行顺应性调整运动;

(7)过程状态s7。由图5可知,该状态是由状态s5至状态s8的过渡状态;

(8)过程状态s8。最终到达该状态,即完全放置状态。

通过隐马尔可夫获得的浅深度插入控制策略如表1所示。

表1 通过隐马尔可夫获得的浅深度插入控制策略

当浅深度推动运动转变为旋转运动时,沿弹簧方向和绕旋转轴方向的控制策略将由刚性控制转变为柔性控制。此外,笔者还推导出了沿插入轴旋转运动的组合控制策略。

4 测试验证

机械臂装配过程中,为了验证该控制策略能够对机械臂浅深度插入进行很好地控制。笔者拟在多种应用场景中,采用UR10 6自由度机械臂分别开展机械臂浅深度插入实验。

笔者通过机械臂模拟设备采集到的阻尼控制参数如图6所示。

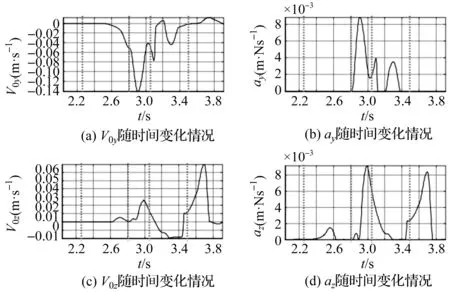
图6 机械臂模拟设备采集的阻尼控制参数v0y,v0z—沿y轴、z轴的标称速度,m/s;ω0x—绕x轴的标称速度,rad/s;ay，az—沿y轴、z轴的通道矩阵元素,m/Ns;arx—绕x轴的通道矩阵元素,m/Ns

隐马尔可夫相对各参数标准差分布如图7所示。

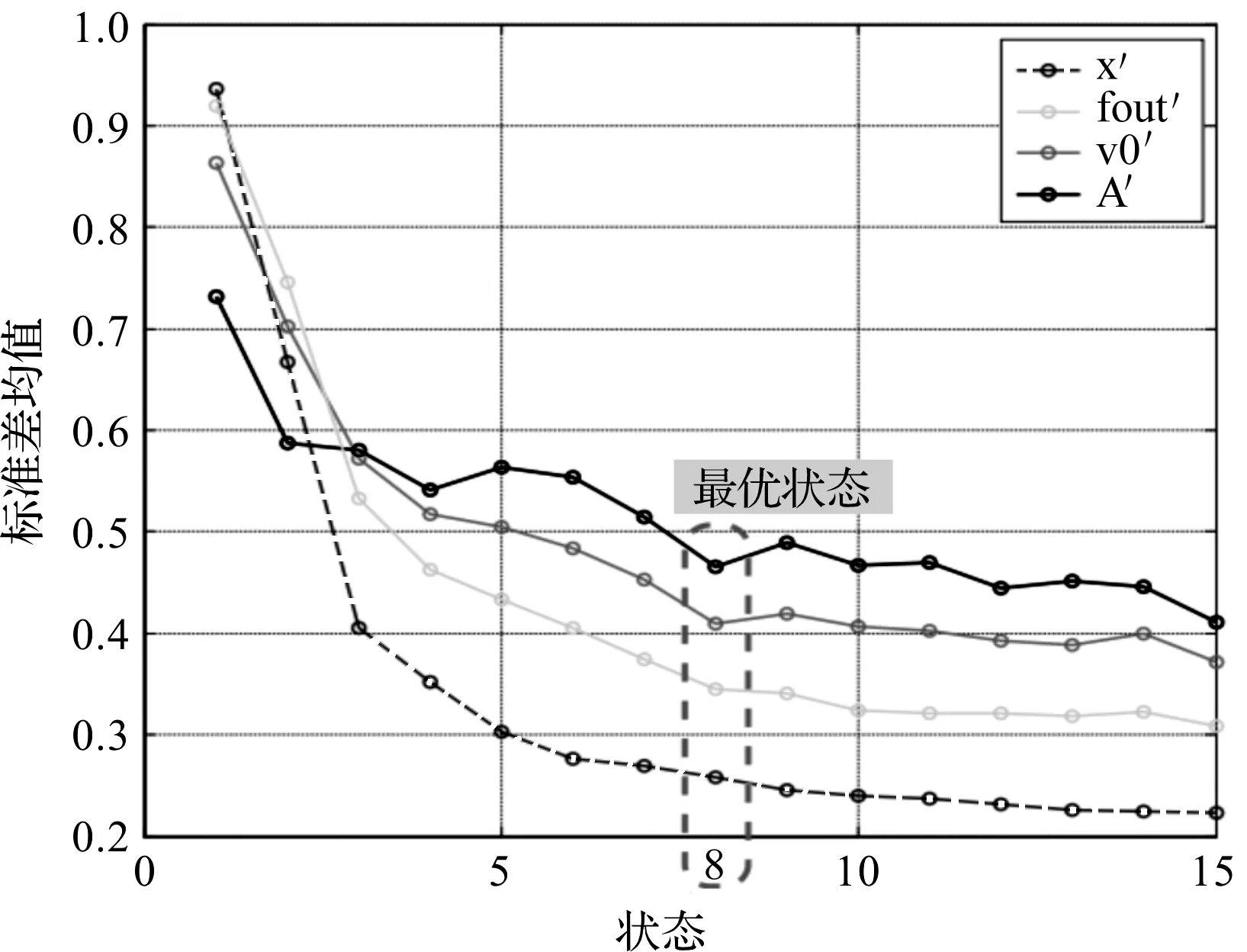
图7 隐马尔可夫相对各参数标准差分布

机械臂设备示图如图8所示。

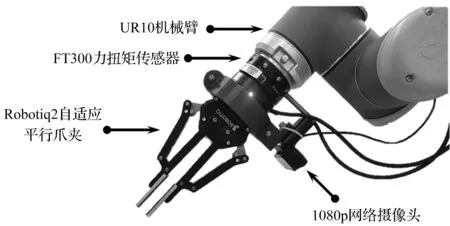
图8 机械臂设备示图

图8中的设备是安装在通用UR10 6自由度机械臂上的Robotiq2自适应平行爪夹器。其传感方式采用FT300力扭矩传感器作为手腕力扭矩传感器,信息采集使用1 080 p网络摄像头进行视觉感知与数据采集。

基于Python编写ROS2包,以实现机械臂浅深度插入控制策略。在该软件包中,定义了3个功能函数,分别为:“倾斜”、“抓握调整”和“放置”,并通过协调机械臂的驱动器来实现。

机械臂“倾斜”行为演示图如图9所示。

图9中,它以旋转中心和倾斜角作为输入,然后控制机械臂执行刚体旋转运动,从而改变放置物与被接触对象的夹角。

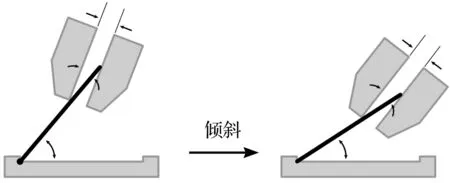
图9 机械臂“倾斜”行为演示图

机械臂“抓握调整”行为演示图如图10所示。

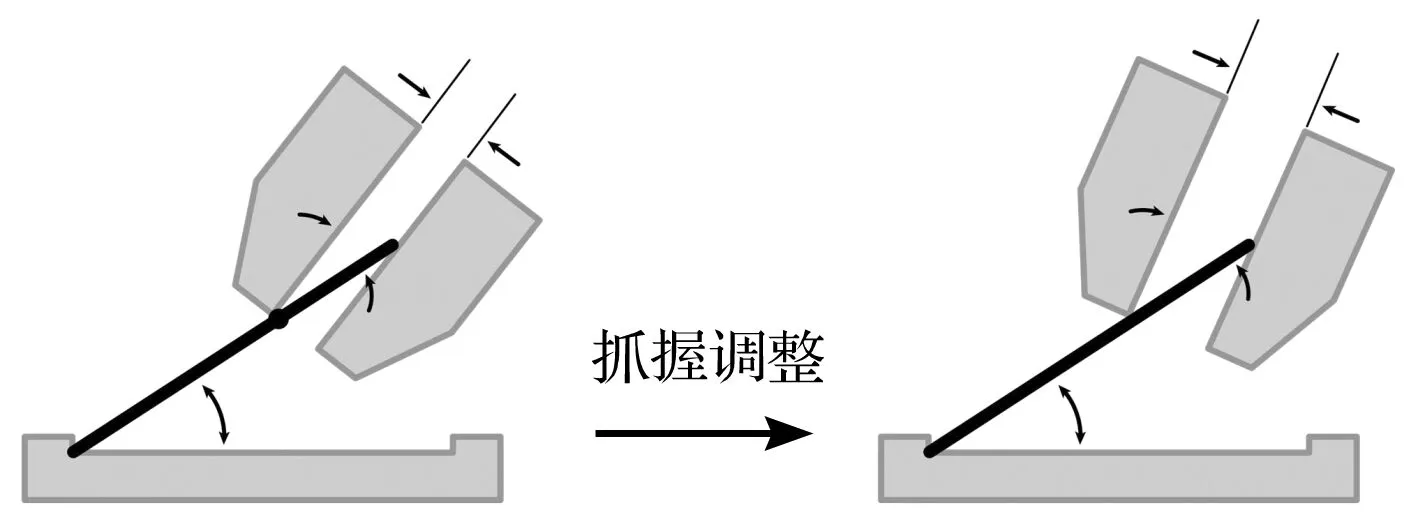
图10 机械臂“抓握调整”行为演示图

该过程主要是针对不同放置物,根据不同被接触对象采取一系列推动和旋转动作。它以旋转中心、期望位移、物体与机械臂的尺寸、物体与机械臂的相对位置作为输入,然后控制机械臂与物体的夹角,而物体与被接触对象的夹角保持不变。

机械臂的“放置”行为演示图如图11所示。

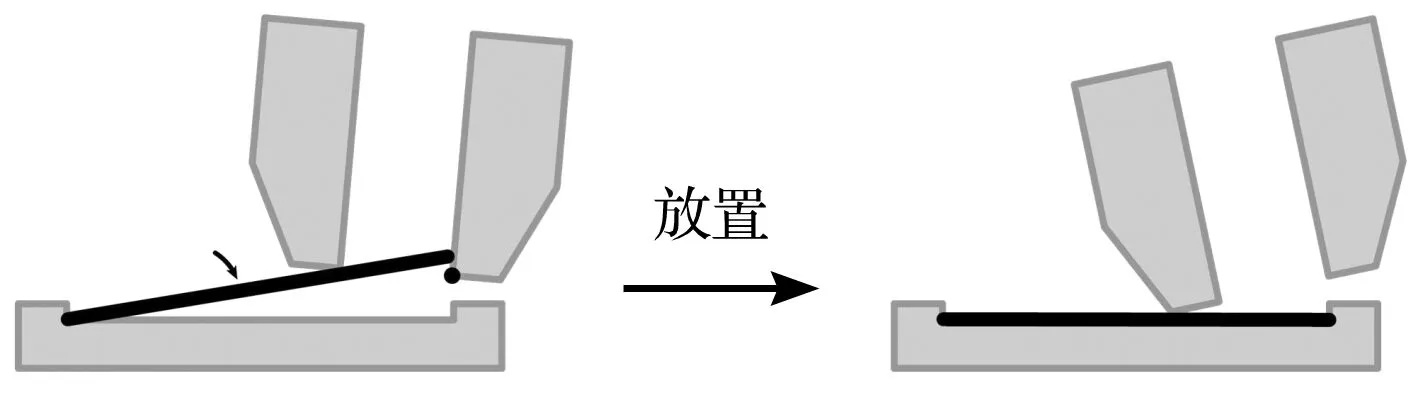
图11 机械臂“放置”行为演示图

由于函数的相似性,可将该方式看作是“倾斜”派生出来的。不同之处在于,机械臂在缩减物体与被接触对象夹角的同时,需要让物体缓缓离开机械臂夹板,直至物体被完全放置于被接触对象上。

然后,笔者通过机械臂进行实际的浅深度插入控制,实现了干电池的装配任务。

机械臂干电池装配测试过程如图12所示。

图12 机械臂干电池装配测试过程

在此基础上,笔者对于手机电池和乐高拼图又开展了相应的浅深度插入控制。

机械臂对手机电池和乐高积木的装配测试过程如图13所示。

图13 机械臂对手机电池和乐高积木的装配测试过程

通过测试可知,机械臂装配过程中,通过笔者提出的基于隐马尔可夫的机械臂浅深度插入控制技术,能够分别在干电池安装、手机电池装配和乐高积木搭建等多种应用场景中很好地实现机械臂浅深度插入控制。

5 结束语

针对浅深度插入装配机械臂难以操控的问题,笔者提出了一种基于隐马尔可夫的机械臂浅深度插入控制策略,并在多种应用场景中,采用UR10 6自由度机械臂分别开展了机械臂浅深度插入实验。

研究结论如下:

(1)基于人工操作数据采集浅深度插入力控参数,基于实测的人工操作数据,识别演示中力控参数的时序数据,利用阻尼控制律对人工操作过程进行建模;结果表明,人工操作数据能够等效为机械臂行为,有助于机械臂控制策略的获取;

(2)利用隐马尔可夫模型对力控参数的时间序列数据进行建模,得到了用于机械臂浅深度插入的控制策略;结果表明,该策略可以由隐马尔可夫模型在各个状态下的符号输出概率表示,有效避免控制行为输出符号的量化误差;

(3)通过分析得到的控制策略,推导出了机械臂为完成浅深度插入装配任务所需的基本动作,如匹配、推动、旋转和放置等;结果表明,该项研究能够实现机械臂对干电池安装、手机电池装配和乐高积木搭建等多种应用场景的自如控制。

在今后的工作中,笔者将继续对需要根据应用场景随时切换控制策略的机械臂装配任务开展深入研究,并通过对其他装配任务的实践分析,为机械臂积累更为有效的控制策略。