双机驱动振动系统的麻雀优化滑模同步控制*

贾一君,张 楠,安兆喆,吴世玲

(北京建筑大学 城市轨道交通车辆服役性能保障北京市重点实验室,北京 102616)

0 引 言

同步是自然界中一种广泛存在的现象。机械振动系统的同步是指振动系统中两个或者多个运动部件以相同或者相近的速度或者角速度运行[1]。20世纪60年代,苏联科学家BLEKHMAN I I[2,3]对双电机的振动同步问题进行了研究,并提出了振动系统自同步理论。

我国学者闻邦椿院士等人[4-7]在自同步理论研究中引入了小参数平均法,对同一平面内双电机振动同步问题进行了研究,并得出了系统同步性条件与稳定性条件。张学良等人[8-11]设计了平面单质体三机及多机驱动自同步振动系统。田晓冲等人[12]针对四电机驱动的振动筛进行了同步性研究及力学分析。陈晓哲等人[13]将机体排布方式从平面引至空间,研究了双机同轴排布的自同步振动理论。方潘等人[14]对空间三机振动同步系统进行了研究,得到了两同轴电机与第三电机排布位置及转子质量对同步性、稳定性的影响。

随着现代同步理论的发展以及对振动系统同步状态精度要求的提高,诸多新型算法被引入振动系统同步控制之中。DONG C F等人[15]将模糊算法与PID参数整定相结合,设计了基于主从控制结构的系统同步控制器。姜娇等人[16]采用矢量控制策略及PI控制算法,实现了反向转动双机驱动振动筛电机的快速反应。黄志龙等人[17]提出了一种相邻交叉耦合控制策略,实现了四激振器激励下,振动机械-物料系统的精确控制。

上述同步控制的实现依赖于大量人工经验和复杂的控制结构,且存在控制精度不高、达到稳态所需时间较长等问题。因此,利用新型智能优化算法简化控制结构、代替人工经验、实现高精度控制等具有一定的实际意义。

麻雀搜索算法(sparrow search algorithm,SSA)主要是根据自然界中麻雀特有的觅食以及反捕食行为规律,加以改进得到的一种新型智能算法[18]14-15。

笔者将麻雀算法与直流电机滑模控制相结合,设计出基于主电机转速和主从电机相位差的同步控制器,对双机驱动机械振动系统主从电机进行转速与相位差的高精度控制。

1 系统动力学模型

1.1 双机驱动振动系统动力学模型

双机驱动振动系统在结构上由刚性振动壳体、激振器、支撑弹簧组成,激振器1、2呈平面对称排布,支撑弹簧对称安装在固定架上。

在系统稳态工况下,两个激振器进行速度相等、方向相反的圆周运动。

双机驱动振动系统动力学模型如图1所示。

图1 双机驱动振动系统动力学模型m1,m2—偏心转子质量;O1,O2—偏心转子回转中心;r1,r2—偏心转子回转半径;φ1,φ2—偏心转子相位

为简化分析,笔者在图1中用偏心转子表示激振电机。

系统的动能为:

(1)

式中:m—机体质量;Jm—机体转动惯量;Ji—激振器偏心转子绕各自回转中心的转动惯量;xi,yi—激振器偏心块在Oxy坐标系中的横纵坐标。

yi可具体表示为:

xi=x+(licosβi+rcosφi)cosψ+(lisinβi+rsinφi)sinψ
yi=y-(licosβi+rcosφi)sinψ+(lisinβi+rsinφi)cosψ

(2)

式中:βi—振动系统偏心转子回转中心到机体质心的连线与x轴夹角。

系统的势能为:

(3)

式中:ky,ky—x向、y向弹簧刚度;Lx,Ly—机体质心到x向、y方向弹簧连接点的距离。

系统能量散逸函数为:

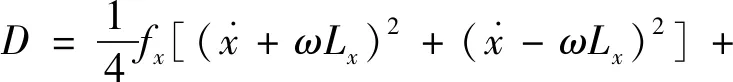
(4)

式中:fx,fy—x向、y向弹簧阻尼系数;fi—激振电机各转轴的阻尼。

对于整个系统,其拉格朗日方程为:

(5)

系统的广义力为:

Qi={Qx,Qy,Qz,Qφ1,Qφ2,Qφ3,Qφ4}T

(6)

其中:Qx=Qy=Qz=0;Qφi=Tei，Tei—激振电机的电磁转矩。

笔者将求得的系统动能方程、势能方程以及能量散逸函数表达式代入拉格朗日方程,可以得到系统x,y,ψ向的运动微分方程和两个偏心转子的回转方程:

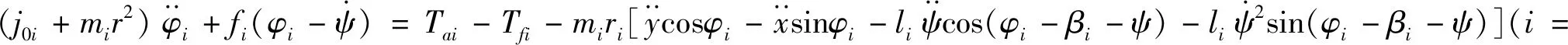
(7)

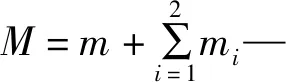
1.2 直流电机数学模型

在电机选择方面,考虑到直流电机有结构简单、制造容易、维护方便、运行可靠等特点,并且相对于交流电机,直流电机在启动、调速、制动、协调运转方面的性能更优,笔者采用直流电机驱动方式,以满足实际应用的复杂性与合理性。

为了主要研究振动系统稳定时的同步情况,笔者将直流电机的电枢电阻设置为常值函数,直流电机机械特性方程如下:

(8)

式中:Tm—电机电磁转矩;Tf—电机负载转矩;J—电枢转动惯量;ω—电机转速。

电磁转矩与电枢电流有如下关系:

Tm=Ktφia

(9)

式中:φ—电机磁极的磁通量;Kt—电机结构常数;ia—电枢电流。

2 麻雀优化变结构滑模控制器

双机驱动振动系统的控制系统主要包括双机驱动机械振动系统动力学模块、主从控制器、直流电机-偏心转子模块。

双机驱动振动系统控制系统框图如图2所示。

图2 双机驱动振动系统控制系统框图

首先,笔者设定目标转速ω,直流电机1(即主电机)转速ω1与目标转速ω相比较后,经主电机角速度控制器处理得到主电机电流信号i1,电流信号经主直流电机-偏心转子模块得到电磁转矩Te1、转子相位φ1等相关参数信号，进入双机驱动振动系统力学模块;

同时,直流电机2(即从电机)转速积分后得到相位φ2,与主电机相位φ1相比较后,经从电机相位控制器处理得到从电机电流信号i2,电流信号经从直流电机-偏心转子模块得到电磁转矩Te2、转子相位φ2等相关参数信号，进入双机驱动振动系统力学模块。力学系统解算得到系统x、y、ψ运动信号返回直流电机-偏心转子模块。

2.1 指数趋近率滑模

滑模变结构控制是一种针对复杂控制系统设计的变结构控制策略,可以实现被控系统在切换面沿设定轨迹滑动直至趋于稳定的效果。滑模运动包含两个阶段,即趋近运动和滑动模态。系统从任意初始状态向切换面趋近,最终运动至切换面的过程叫做趋近运动,即s→0。

根据滑模变结构原理,滑模可达性条件只能确保任意一位置的运动点在空间中的有限时间内到达切换面,但并不规定其具体的运动轨迹。因此,可以尝试利用趋近率的方法确保趋近运动过程中的动态品质。

指数趋近率的作用可以看作:使趋近速度逐渐由一个相对较大值向0趋近,这个过程所耗时相对较少,且运动点可以以一个相对较小的速度到达切换面,采用如下形式的指数趋近率:

(10)

式中:E1，k1—均为正数。

2.2 主电机转速控制器设计

取主电机状态变量为:

(11)

式中:ω*—给定转速;ω1—主电机转速。

将式(8，9)代入式(11),并对其进行求导,可得:

(12)

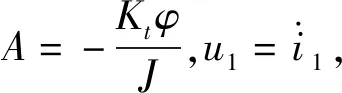
(13)

系统滑模面为:

s=c1x1+x2

(14)

c1为正数,满足Hurwitz条件。

由式(10，14)可得控制量i1表达式:

(15)

2.3 从电机相位控制器设计

取从电机状态变量为:

(16)

系统滑模面为:

(17)

同样,采用指数趋近率,有:

(18)

式中:E2，k2—均为正数。

由以上式子可得控制量表达式:

(19)

2.4 主电机麻雀优化变结构滑模控制

麻雀算法具有寻优能力强、收敛速度快等优点,是一种新颖的智能算法。利用麻雀算法对式(15)中E1、k1进行参数寻优,可以取得较好的抑抖效果和趋近速度。

设计适应度函数为:

F=0.5|s|

(20)

在麻雀群体中有发现者与加入者两种类型的麻雀,发现者负责寻找食物并报警给群体提供觅食方向,加入者根据发现者提供的信息不断更新自身位置直至获取食物[18]16-18。

假设群体中共有n只麻雀,待优化变量数量为m,则群体初始位置X表示为如下形式:

(21)

发现者根据如下规则不断向最优位置Xi,j搜索迫近:

(22)

式中:t—迭代次数;itermax—最大迭代次数;R—预警值;ST—安全值;Q—服从正态分布的随机数;L—元素全部为1的1×m的矩阵。

其中:i=1,2,3,…,n;j=1,2,3,…,m。

加入者根据如下规则不断更新位置Yi,j:

(23)

式中:Yw—全局最差位置;Yp—当前搜索条件下全局最优位置。

其优化流程如图3所示。

图3 麻雀优化变结构滑模控制系统框图

经过一定次数的迭代后,麻雀算法给出当前时刻下最优的切换项系数E1、K1。

3 同步控制系统仿真分析

为了验证该系统控制同步设计的合理性,笔者利用Simulink搭建电机-振动系统仿真模型,如图4所示。

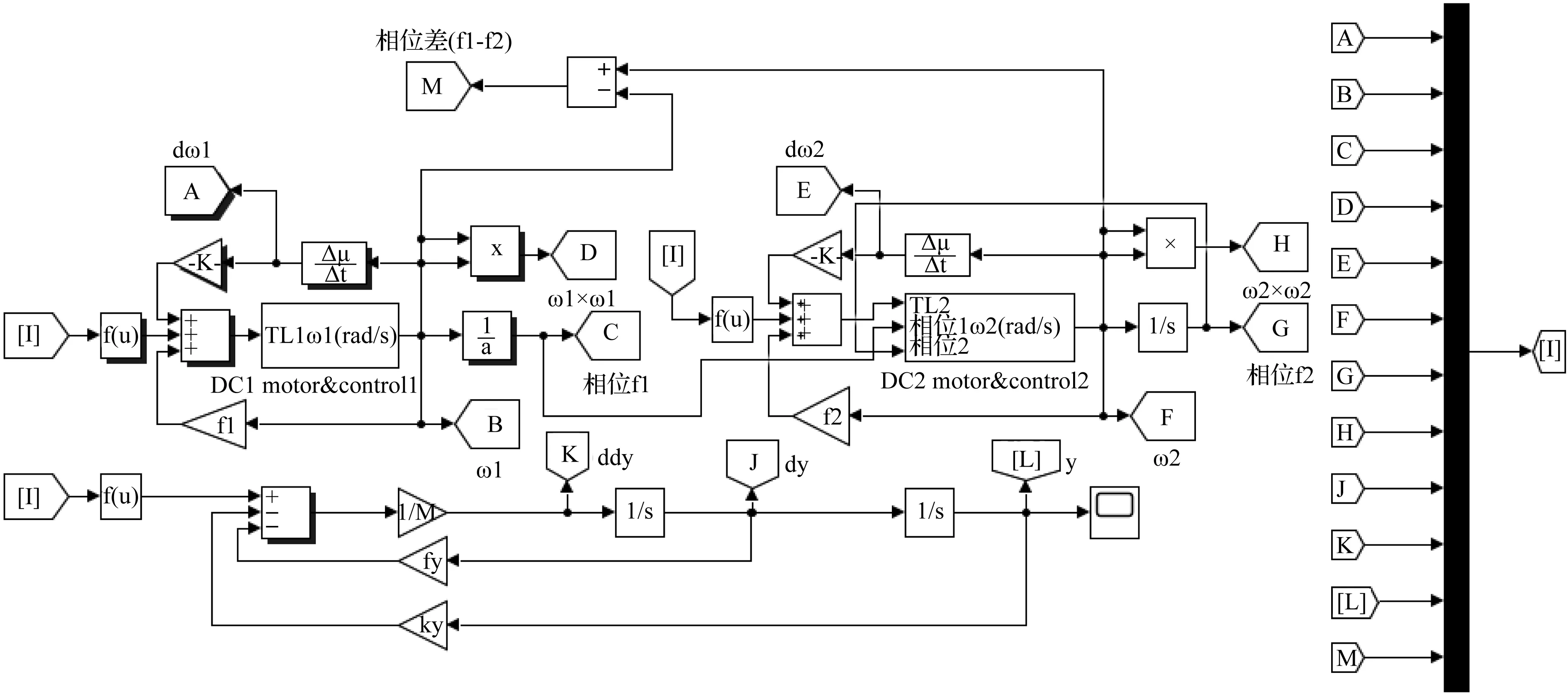
图4 双机驱动振动系统同步控制仿真模型

采用龙格-库塔算法和变步长控制策略,系统仿真参数如表1所示。

表1 振动系统仿真参数

当主、从电机角速度与相位差均趋于稳定,则振动系统进入同步状态[19]。

同步控制仿真实验结果如图5所示。

由图5(a)可以看出,主电机角速度(图5(a)中用实线表示)在经历0 s～20 s的调整阶段后,平滑到达预设定的角速度20 rad/s;从电机角速度曲线(图中用虚线表示)在滑模控制器作用下跟随主电机角速度平滑达到预设定的角速度,且实现了较好的跟踪效果;

图5 同步控制仿真实验结果

图5(b)显示两电机相位差最初为-2 rad,在滑模控制器的作用下,两电机相位差在经历一个较大波动后也实现稳定,最终稳定在0 rad左右;

图5(c,d)为机体x、y方向位移。图5(c)表明:在经历了约40 s的调整阶段后,机体x方向位移最终趋于0,振动系统x方向趋于静止;

图5(d)表明:在经历了约30 s的调整阶段后,机体y方向位移最终趋于-0.02 m～0.02 m的弦类往复波动;

图5(e)为机体整体位移,从中可以看出,在经历一段时间的无规律波动后,振动系统逐渐过渡为x方向位移为0、y方向位移为-0.02 m～0.02 m的弦类往复波动(图中线条密集部分);

图5(f)为振动机体Ψ方向摆动,最终为小范围内的稳态弦类波动。双机驱动振动系统主要应用于直线式往复振动工作场合。

图5结果表明:系统设计满足生产实际要求,且主从电机角速度、相位差以及振动系统整体运动均处于稳定状态,可见双机驱动振动系统的麻雀滑模同步控制是有效的、稳定的。

4 结束语

笔者应用Lagrange方程建立了双直流电机驱动型振动系统的机电耦合模型,设计了基于主电机角速度差与主从电机相位差的主从变结构滑模控制器,并利用麻雀优化算法对主电机滑模切换项系数进行了优化。

研究结果表明:

(1)采用麻雀优化滑模控制算法可以将主电机转速与预设转速之差控制在0.5 rad/s之内;从电机转速跟踪效果较好,主从电机相位差可稳定在0.1 rad之内;

(2)在主从电机控制器作用下,振动机体水平方向基本维持不动,竖直方向表现为-0.02 m～0.002 m的稳态弦类波动,满足振动类机械实际工作的要求。

实际研究发现,在振动机械的生产作业中,为满足差异化工艺需求,往往需要3台及以上振动电机同步工作。

在后续的研究中,笔者计划将麻雀滑模控制算法应用于对多台电机的同步控制之中。