基于零力矩点理论的汽车起重机稳定性研究*

周庆辉,张晨龙,刘耀飞,3,张希望,谢贻东,李 欣

(1.北京建筑大学 机电与车辆工程学院,北京 100044;2.北京市建筑安全监测工程技术研究中心,北京 100044;3.中铁建设集团有限公司,北京 100040;4.北京市机械施工集团有限公司,北京 100045)

0 引 言

由于其灵活的机动性,汽车起重机在建筑施工领域得到了广泛应用[1]。在起重机实际施工过程中,复杂的环境以及许多不确定因素会造成起重机失稳倾覆,导致事故的发生。

在所有的起重机事故中,汽车起重机事故约占84%[2]。因此,汽车起重机的稳定性一直是现场安全管理的重要方面,也是学者关注的热点。

FUKAGAWA A R等人[3]分析了地面变形对汽车起重机倾覆性的影响,并设计了相应的报警系统。TOWAREK Z[4]在考虑了吊臂旋转的基础上,建立了汽车起重机的动力学模型。GIUSEPPE等人[5]采用刚体静态理论,对起重机的稳定性进行了分析,并提出了一种在重物提升期间监测起重机实际稳定性的方法。KACALAK W等人[6]利用现代CAD/CAE计算技术,通过分析所吊装货物的移动,对起重机装卸系统的稳定性进行了评估。王伟等人[7]通过研究,给出了理想条件下起重机的防倾翻检测方法。SHAIKH A A[8]通过配置起重机的可移动配重,在保持其稳定性的同时,提高了起重机的站立力矩与起重能力。方维等人[9]利用ADAMS软件,构建了QY20汽车起重机的动力学仿真模型。谢飞[10]对斜坡工况下汽车起重机的工作稳定性进行了仿真研究。张成等人[11]利用“贡献矩”原理法,对汽车起重机的支腿反力进行了计算。

在这些起重机稳定性的计算中,力矩法是最常用的方法。但由于力矩法数学模型本身存在局限,即缺少对动载荷的考虑,力矩法会导致一定的误差。

在对汽车起重机进行的抗倾覆稳定性分析中,载荷摆动、振动等因素引起的动载荷是不可忽视的。因为在起重机处于吊装载荷极限的时候,钢丝绳的摆动、回转速度变化、重物升降等吊装情况的动态变化,这些因素都极有可能造成汽车起重机整机倾覆。

零力矩点(zero moment point,ZMP)是判定动态稳定运动的重要指标。YU B H等人[12]利用ZMP理论,对挖掘机抗倾覆动态稳定性问题进行了研究。靳立强等人[13]基于零力矩点位置和模糊控制,对商用车的防侧翻控制进行了研究。夏光等人[14]基于ZMP理论,对平衡重式叉车防侧翻模型进行了研究。

笔者采用零力矩点理论,对汽车起重机抗倾覆稳定性进行研究,具体分析吊重摆动、变幅运动和回转运动对起重机最大起重量的影响,提出一种基于ZMP理论的起重机稳定性检测方法。

1 汽车起重机模型

1.1 物理模型

汽车起重机的倾覆稳定性计算模型如图1所示。

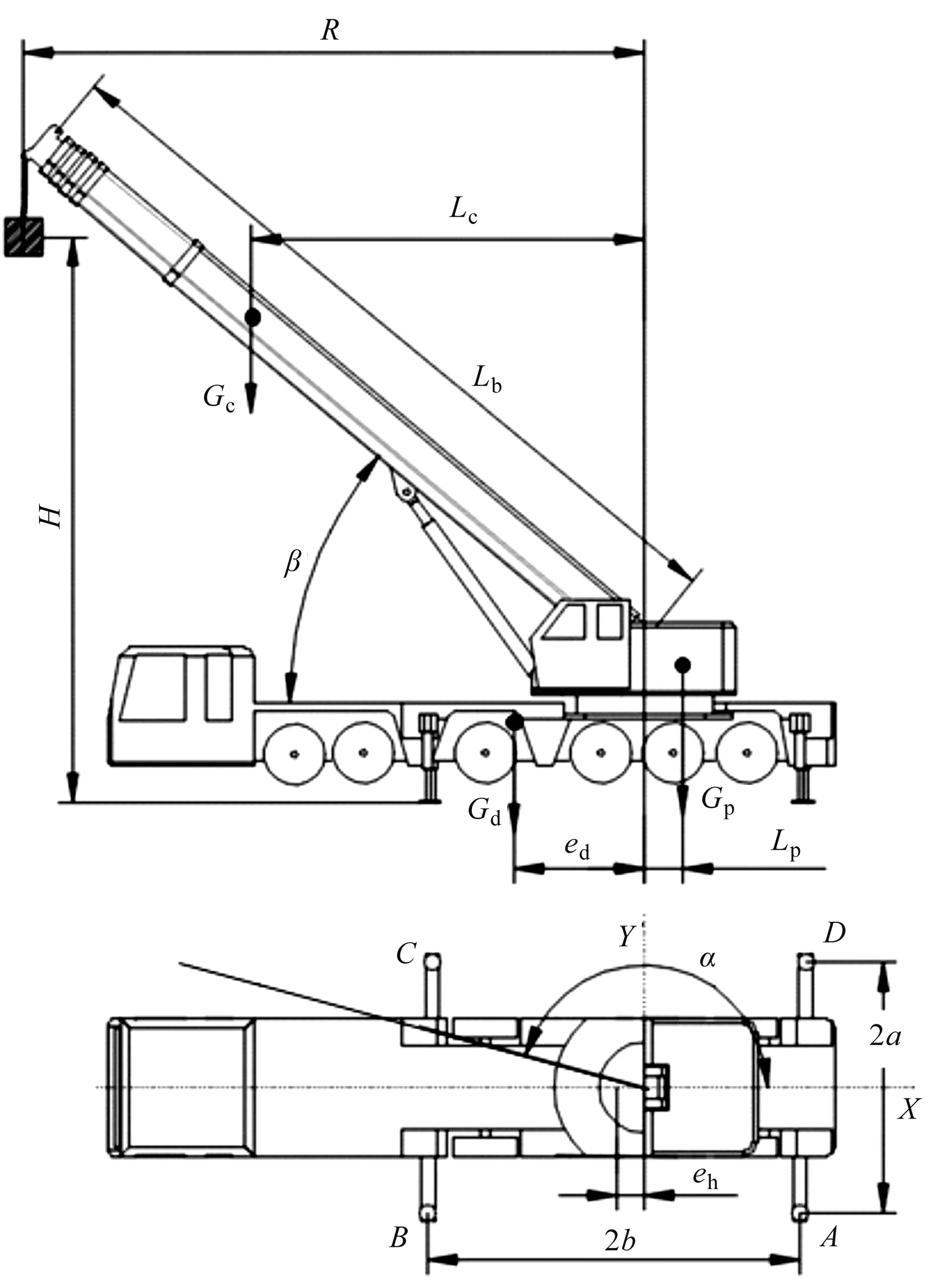
图1 汽车起重机模型

为了方便计算,此处假设汽车起重机的主体及吊臂为刚体,地面基础为刚性结构,视吊物为质点;忽略支腿中心线相隔的距离,忽略臂架各节臂重心位于臂架几何中心位置,忽略旋转过程中产生的摩擦力矩。

汽车起重机在吊装作业时,按4个支腿进行支撑。汽车起重机各符号的含义如表1所示。

表1 各符号含义

1.2 起升能力计算

零力矩点(ZMP)是指在某一时刻,在支撑面上,汽车起重机重力、外力和惯性力的合力没有水平分力的那一点。零力矩点ZMP落在支撑面内,可保证汽车起重机运动过程的稳定性。

重力和惯性力的合力为:

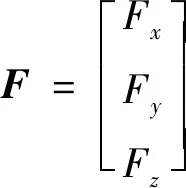
(1)

该合力对各个坐标轴的矩为:

(2)

将合力从参考坐标系原点移动到ZMP点(ZMP点处合力矩对X,Y轴分量为零),则有:

(3)

由此可得到:

(4)

以回转轴与地面交点为坐标原点建立直角坐标系,可以得到起重机各部分质量质心坐标;将得到的各部分的质心坐标值和质量代入式(4),可以计算出零力矩点(ZMP)在x,y轴的坐标值xzmp、yzmp。

在实际的计算中,需要根据汽车起重机4个支腿位置及安全裕度来确定ZMP的稳定区域[15],依据式(3)反向推导出ZMP点与起重量的关系,然后依据ZMP稳定区域的限制,求出最大起重量。

当惯性力为0时,汽车起重机为静态稳定运动,如图2所示。

图2 静态稳定运动时,ZMP与重心投影点的变化情况

图2中,当吊装作业的工作幅度为7.32 m,吊重为8 000 kg;吊臂回转一圈,工作台回转角度从0°～360°变化时,ZMP和重心投影点分别随回转角度变化。

由图2可知:ZMP与重心投影点重合,ZMP和力矩法得到的结果是相同的。

某QY25型的主要参数数值如表2所示。

表2 某QY25型汽车起重机的主要参数值

1.3 动力学模型

在施工中,汽车起重机回转动作会经常启动、停止,吊重也会频繁起升、降落,从而不可避免地产生惯性力,导致起重机的吊重摇摆。倘若ZMP正好落在倾覆边而处于临界条件,吊重摇摆产生的惯性力将会造成ZMP向外偏移,从而导致汽车起重机整机的倾覆。

为了分析吊重摇摆运动时对起升能力的影响,需要对汽车起重机建立动力学模型。

汽车起重机以回转中心做原点;回转角度α按顺时针旋转方向为正;x轴的正方向是起重机的车头方向;y轴的正方向是起重机的左侧方向;则x、y、z坐标系如图3所示。

图3 汽车起重机动力学模型θ1—切向摆角,rad;θ2—纵向摆角,rad;Lb—吊臂长度,m;l—钢丝绳长,m;α—回转角度,rad;β—工作幅角,rad

此处以切向摆角θ1和纵向摆角θ2做广义坐标进行受力分析,代入Lagrange方程中,即:

(5)

式中:t—时间;T—系统动能;V—系统的势能;L—拉格朗日算子,L=T-V。

将各参数代入公式,系统两方程变为如下形式[16]:

(6)

式中:g—重力加速度,m/s2。

(7)

由于摆角比较小,简化摆角的无穷小量,得到了回转运动时的汽车起重机动力学模型如下:

(8)

2 动力学模型求解

根据吊重摆角的运动,利用式(8)可以得到吊重加速度、吊臂回转加速度等参数值,将其代入到式(4)中,可以分别计算出起重机静态稳定运动与动态载荷变动时的最大起重量。

静态与动态时,汽车起重机最大起重量的对比如图4所示。

图4 静态与动态时,起重机最大起重量对比

图4为当吊重发生摆动时,吊臂回转一圈,回转角度从0°到360°时最大起重量的对比图。

由图4可见,吊重摆动导致载荷动态变化,得到的最大起重量将小于静态时的数值。这是由于载荷动态变化使得运转零部件质心处附加了瞬时加速度,产生了惯性力,从而使起重机的起升能力比静载荷时要小。

3 模型求解验证

3.1 静态最大起重量实验验证

考虑到人员安全和实验条件,对汽车起重机进行倾覆性真实实验的风险和难度较大。因此,笔者采用某汽车起重机的等比缩放模型,进行起重机最大起重量验证实验。

汽车起重机模型如图5所示。

图5 汽车起重机模型

笔者对该模型按照起重工况的实际工作参数进行起重量加载实验。

该模型起重工况臂长为200 mm,变幅转角为45°,回转角度分别取0°、30°、45°、60°、90°、120°、145°、150°、180°;在吊钩的竖直方向上,吊装有重量标识的砝码,逐渐增加吊装的重量,直至发生倾覆失稳,得出静态最大起重量。

根据ZMP方法得到汽车起重机的最大起重量如图6所示。

图6 最大起重量图(单位:g)

图6中,圆点是实验得到的最大起重量。ZMP得到的最大起重量与实验结果具有很好的吻合度,在0°、45°、90°、135°、180°时,汽车起重机最大起重量和实验结果基本一致;

在回转角度30°、60°时,起重机最大起重量略大于理论计算值;在回转角度120°、150°时,最大起重量略小于计算值,这是由于汽车起重机在偏后方作业比在偏前方作业的稳定性相对要好。

3.2 QY25型汽车起重机的计算验证

起重量特性表中的起重量是起重机械在正常工作情况下所允许的最大起重量,是起重机生产厂家根据多年设计经验积累出来的,是起重机设计、选型、施工和运维重要的参考依据。

根据表中的起重工况,笔者利用ZMP理论进行了计算,得出最大起重量,和表中数据进行比较,可以验证理论模型的正确性。

当某QY25型汽车起重机臂长为17.68 m时,根据不同的变幅角度,可以得到理论计算最大起重量,如表3所示。

表3 QY25型汽车起重机最大起重量对比

由表3可知,理论计算值和起重特性表中值具有很好的相关性,起重机最大起重量随变幅角度的减小而减小。

但特性表中的数值相对偏小,这是因为起重特性表的设计充分考虑到了起重机的各种特殊工况的稳定性,因此笔者选取了较大的稳定安全系数,即以牺牲部分起重能力为代价,换取较高的安全稳定性。

4 最大起重量的影响因素

4.1 吊重摆动的影响

在QY25型汽车起重机中,笔者选取基本臂长10.4 m,工作幅度分别为5.5 m、6.0 m和6.5 m。

在正后方作业时,起重机钢丝绳长度为5 m,摆角控制在20°以内。

起重机最大起重量变化如图7所示。

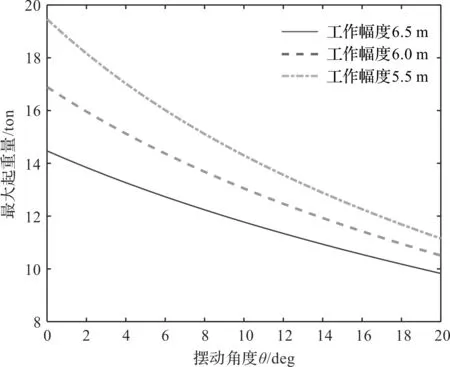
图7 最大起重量随摆角变化图

吊重的摆动对起重机的最大起重量影响较大,随摆角的增加,最大起重量减小;

在同一工作幅度如6.5 m时,摆角为0°,起重机最大起重量为14.4 t;当摆角达到20°时,最大起重量大约减少了4.7 t。

4.2 变幅运动的影响

保持吊臂长度为17.68 m,变幅角度分别为45°、50°、55°时,最大起重量的变化如图8所示。

图8 臂长17.68 m,变幅时汽车起重机的最大起重量(单位:t)

在吊臂旋转一圈,回转角度从0°～360°变化时,最大起重量随着变幅角度的减小而减小,各最大起重量图形和变化趋势基本相同,并呈现出由外到内的包含关系。这也符合实际作业情况,即吊臂起升角度越小,起重能力越小;当吊臂水平时,起升角度为0°,起重能力最低。

4.3 回转运动的影响

在图8中还可以看出:吊臂在0°～360°的回转过程中,随回转角度不同,零力矩点ZMP所落的区域不同,起重机失稳的临界边界也不同,起重机的最大起重量也随之变化。

例如:在支腿附近区域作业,起重机的起升能力最强,最大起重量的数值也最大。同时,回转运动的频繁启动、停止,会产生回转加速度,导致吊重的摇摆,xzmp(或yzmp)将减小,最大起重量也随之减小。

5 防倾覆检测方法

在汽车起重机中,起重臂长度传感器、变幅油缸起升角度传感器、回转角度传感器可以分别实测出实际臂长、实际变幅角度和实际回转角度,根据ZMP理论,能够计算得到各工况最大起重量。

同时,吊重传感器可以测量出实际起重量。这样,能够与计算得到的最大起重量进行比较,一旦实测起重量超过最大起重量时,就可以报警或强制制动,避免超载,防止倾覆,以保证整机稳定性。

笔者用指数Smoment表示实测起重量Qr与最大起重量Qmax的比值,即:

(9)

根据式(9),可以计算得到不同变幅角度时,Smoment随回转角度变化的曲线,如图9所示。

图9 Smoment变化图

Smoment数值越接近1,倾覆可能性越大,作业越危险。

图9中,变幅角度在25°时,Smoment最大值为0.97;而在变幅角度为65°时,Smoment最大值仅为0.20,因此变幅角度越小,也倾向于倾覆失稳,作业也要更危险;

在相同的变幅角度均为25°时,回转角度位于90°和270°时,也就是吊臂在正侧方作业位置时,起重机危险性最大;而吊臂在支腿附近作业时,危险性最小,相对最安全。

6 结束语

针对汽车起重机的稳定性问题,笔者采用ZMP理论建立了汽车起重机的动力学模型,提出了一种基于ZMP理论的最大起重量计算方法;并通过实验的方式验证了ZMP理论的可靠性,通过分析不同运动参数对最大起重量的影响,为工程应用提出了一种基于ZMP理论的稳定性检测方法。

研究结果表明:

(1)通过ZMP理论,计算得到了起重机各工况的最大起重量;利用ZMP理论分析了各个运转零件质心的加速度,考虑了动载荷的影响,提高了模型的准确性;

(2)对汽车起重机等比缩放模型进行了模拟实验,其结果表明:ZMP最大起重量理论值与模拟实验值具有很好的吻合度;

(3)起重量特性表是重要的技术依据,是厂家多年积累的技术经验。根据汽车起重机的起重量特性表,验证了ZMP理论模型的准确性;

(4)提出了基于最大起重量的防倾覆检测方法,可通过比较实测起重量与ZMP理论计算值,实现对起重机倾覆的预警,提高了起重机整机的稳定性。

在后续的研究中,笔者将进一步分析不同地面特性下，地面失稳对汽车起重机稳定性的影响,以扩大ZMP理论的稳定性计算及防倾覆检测方法的应用范围。