基于一维全变分的液压系统压力信号快速实时去噪方法*

黄泽雄,李海艳,甘华权,刘 云

(广东工业大学 机电工程学院,广东 广州 510006)

0 引 言

随着工程车辆自动化的发展,装载机、伸缩臂叉车以及液压挖掘机等工程车辆/机械,以降低工作效率为代价的传统静态载重估计方式,已不能满足现阶段先进的工业现场要求。

目前,研究较多的动态载重估计方法是通过测量工程车辆动臂升降过程中液压缸的压力信号,结合工程车辆的结构参数和几何参数,利用相关的静力学分析和动力学分析,以此来间接动态地估计出载重[1-5]。

由于工程车辆的作业环境恶劣,操作工况复杂,工程车辆的振动、动臂升降时的惯性冲击,以及液压信号本身的非线性关系,都会造成其液压信号的大幅度振荡;同时,工程车辆在作业过程中会源源不断地产生数据信号。

因此,若能实时处理非线性的非平稳液压信号,准确地测量出载重时的液压信号,就能够为工程车辆后续的精确载重估计提供帮助。

采用EMD、小波阈值进行非平稳信号重构和去噪,一直是信号处理领域的研究热点。

王伟等人[6]提出了一种基于EMD的装载机载重动态测量信号处理方法,即对装载机在举升过程中的动臂液压缸实测液压信号进行EMD分解,然后直接提取其低频残余量进行信号重构;但这种方法会丢失本征模态函数(intrinsic mode function,IMF)高频分量中的有用信号。马宏伟等人[7]提出了一种基于EMD的振动信号去噪方法,即通过计算各IMF与原始信号的相关性系数,并将其按照从小到大进行排序,取相邻2个相关性系数差值最大之前的敏感IMF分量进行信号重构。易文华等人[8]在融合EMD的自适应性和主成分分析(principal component analysis,PCA)的完全正交性特点的基础上,提出了一种自适应性正交经验模态分解(principal empirical modedecomposition,PEMD)的信号去噪方法。

但是这两种方法缺少严谨的理论证明,即真实IMF与原始信号的正交程度高,则相关性较好;虚假IMF与原始信号的正交程度差,则相关性较差。

高春甫等人[9]提出了一种基于小波分解的信号冗余实时去噪算法,但该方法需要采集更多的数据,然后再采用固定的数据窗对液压信号进行实时去噪处理。钟建军等人[10]通过计算信噪比和均方根误差(root mean square error,RMSE),并将其作为小波阈值去噪结果的客观判据,从而获取了最佳的小波函数和阈值规则匹配组合,解决了不同小波基匹配不同阈值规则,可能会影响去噪效果的问题;但这种小波阈值去噪方法需要针对不同特点的含噪声信号,而选取不同的小波基与阈值规则的组合,因而该方法缺乏自适应性。王强等人[11]提出了一种将小波分解与自适应滤波相结合的流体压力信号去噪方法,但是采用该方法在小波分解后得到各频带下的信号,需要设定各自适应滤波器参数,其参数的设置过于复杂。

1D TV算法[12]具有快速、非迭代和逐点扫描的特点,因此,笔者将其应用于工程车辆的载重估计模型中,进行非平稳液压信号的实时去噪。

笔者首先建立一个主要受液压力影响的载重估计模型,并使用MATLAB内嵌的fmincon非线性规划求解器,最小化载重估值与载重真值之间的均方根误差,优化求解出1D TV算法中的参数;最后,对不同去噪算法进行对比。

1 一维全变分的基本原理

假设一维离散信号v=(v1,vk,…,vN)∈RN,N≥1,受到噪声w的干扰,则被噪声污染后的信号u为:

u=v+w

(1)

在RUDIN L I等人[13]提出的基于全变分的信号和图像去噪模型基础上,笔者把一维离散信号当作一个最小化问题进行隐式求解,即:

(2)

(3)

其中,式(2)中的τ是一个大于0的正则项参数。因为最小化J(v)是一个强凸函数,所以当梯度J(v*)=0时,式(3)的解v*总是能够存在且唯一。

在此基础上,文献[14]对1D TV算法做出了形象的数学推导,并给出了较为详细的求解过程,即:

(4)

对式(4)等号右边的第一项求梯度,可得:

(5)

(6)

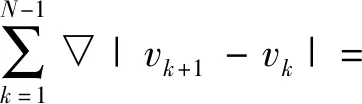
(7)

其中:

(8)

结合式(5)和式(7),得每一个分量▽J(vk):

(9)

(10)

为统一式(10)的数学形式,考虑α0=αN=0,记θk=ταk(k=1,…,N-1),θ0=τα0,θN=ταN。

式(10)可重新写作:

(11)

(12)

从式(11)和式(12)可以看出,参数τ直接关系到式(3)解v*的准确性,从而直接影响1D TV算法处理信号时的去噪效果。因此,有必要讨论如何对参数τ进行优化。

2 一维全变分中参数的优化

不同参数τ对1D TV算法去噪效果的对比情况如图1所示。

图1 不同参数τ对1D TV算法去噪效果的对比

由文献[15]可知,关于参数τ的选择通常是在给定范围内,根据损失函数的大小进行手动调整,进而选取出相对最优参数值。

从图1可以看出:对于不同的参数τ,1D TV算法会有不同的去噪平滑效果,而且参数τ越大,曲线越光滑,但当参数τ过大时,去噪效果反而会下降。

在实际的信号去噪应用中,当无法确定参数τ的大小时,非平稳液压信号也就很难通过1D TV算法去平滑逼近其真实的液压信号曲线。

因此,使1D TV算法在液压信号去噪平滑问题上更具有实用性的关键在于,如何得到最优的参数τ。

2.1 载重估计模型

伸缩臂叉车臂架结构图如图2所示。

图2 伸缩臂叉车臂架结构图1—一节臂;2—二节臂;3—三节臂;4—四节臂;5—叉具;6—载重;7—伸缩缸缸筒;8—伸缩缸缸杆;9—变幅液压缸;10—随动液压缸;l—伸缩臂长度;θ—臂架变幅角度

图2中,臂架结构主要由4个节臂、伸缩液压缸、叉具以及载重等组成(调平液压缸质量很小,可忽略不计)。伸缩液压缸对伸缩臂进行伸缩动作,变幅液压缸为臂架提供推力进行变幅动作,随动液压缸则对臂架提供阻尼力。

由于液压系统中分配阀的特殊结构,伸缩臂是先变幅(或伸缩),后伸缩(或变幅)。因此,臂架的工作过程为:

某段时间内伸缩臂在进行伸缩运动时,伸缩臂长度l改变,在另外某段时间内整个臂架绕基本支承点作变幅运动时,变幅角度θ改变,再考虑在升降载重过程中臂架变幅角加速度很小的运动特点。

故笔者取臂架为隔离体,以车架与一节臂的铰点O为力矩平衡点,伸缩臂叉车的行驶方向为X轴正向,垂直于X轴的竖直向上方向为Z轴正向,建立坐标系XOZ,对臂架进行静力学分析。

根据力矩平衡原理[16],同时假设臂架各构件材质是均匀分布,认为其重心在它们的几何中心,然后结合各构件重心的位置坐标关系和各构件间的几何尺寸关系,可以求得载重大小与变幅液压缸压力、随动液压缸压力的关系式,即:

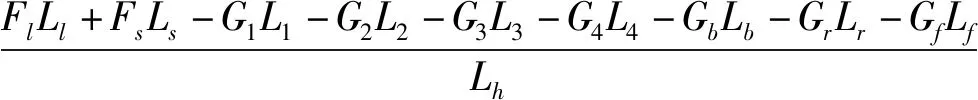
(13)

式中:G1,G2,G3,G4,Gb,Gr,Gf,Gh—一节臂、二节臂、三节臂、四节臂、伸缩缸缸筒、伸缩缸缸杆、叉具以及载重的重力;L1,L2,L3,L4,Lb,Lr,Lf,Lh—相对应构件重力的力臂;Fl,Fs—变幅液压缸、随动液压缸对臂架的作用力;Ll,Ls—变幅液压缸、随动液压缸对臂架作用力相对应的力臂。

变幅液压缸对臂架的推力Fl为:

(14)

式中:Plw,Ply—变幅液压缸无杆腔和有杆腔液压力;Dlw,dly—变幅液压缸无杆腔直径和活塞杆直径。

随动液压缸对臂架的阻尼力Fs为:

(15)

式中:Psw,Psy—随动液压缸无杆腔和有杆腔液压力;Dsw,dsy—随动液压缸无杆腔直径和活塞杆直径。

2.2 参数的优化

从式(13)可以看出,载重估值主要是受到变幅液压缸压力、随动液压缸压力的影响,所以振荡的液压信号曲线通过去噪平滑后,可以减小载重估值与载重真值之间的均方根误差,即最小化其均方根误差,可以间接使经过1D TV算法去噪平滑后的液压信号曲线更接近于真实的液压信号曲线。

MATLAB内嵌的fmincon非线性规划求解器可以寻找约束非线性多变量函数的最小值。fmincon函数的内点算法[17-18]内存使用量少,能够快速求解大型问题。

此处,笔者使用fmincon求解器的内点算法,把经1D TV算法平滑去噪的变幅液压缸压力、随动液压缸压力与载重的关系式作为黑箱函数,载重估值与载重真值之间的均方根误差作为目标函数值,对参数τ进行优化求解。

参数τ的优化流程如图3所示。

图3 参数τ的优化流程

图3中,参数τ的下界τmin设为0,上界设τmax为500,初始值则设为(τmin+τmax)/2。变幅液压缸压力、随动液压缸压力先经过1D TV算法去噪平滑后,再输入到载重估计模型中,然后计算载重估值与载重真值之间的均方根误差;当目标函数值RMSE最小时即可优化求解出最优参数τ,否则继续迭代,直到找到最优参数τ为止。

3 基于实测信号的性能试验

3.1 评价指标

为准确反映EMD类去噪算法、小波阈值类去噪算法,以及经过参数τ优化后1D TV算法对液压信号的去噪平滑效果,笔者在这里使用信噪比(signal to noise ratio,SNR)、互相关系数(cross correlation coefficient,Ccc)以及平方和误差(error of square sum,SSE)分别作为第一、第二、第三评价指标[19,20]。

SNR定义为有用信号功率与噪声功率之比,其公式为:

(16)

式中:uk—原信号;vk—理论信号;k—离散点数。

Ccc定义为原信号与理论信号的互相关系数,可用它作为原信号与理论信号之间的密切相关性,其公式为:

(17)

式中:Cov(uk,vk)—uk和vk的协方差。

SSE定义为原信号与理论信号的能量差,代表波形的总体效应,其公式为:

(18)

由式(16～18)可以看出,SNR越大,Ccc越大,SSE越小,表明算法的去噪平滑效果越好。

3.2 数据的采集

伸缩臂叉车的尺寸和性能参数如表1所示。

表1 伸缩臂叉车的尺寸和性能参数

笔者在试验中采集了当伸缩臂叉车装载3.368 t载重时,随动液压缸压力、变幅液压缸压力、伸缩臂长度以及臂架变幅角度随多工况操作的实时数据。数据采集仪的采样频率为40 Hz,试验数据一共采集200 s。

角度传感器和位移传感器的安装如图4所示。

图4 角度传感器和位移传感器的安装白虚线圈内—角度传感器;白实线圈内—拉绳式位移传感器

试验时,笔者在4节臂安装高性能角度传感器VALUER SpaceVector,实时测量臂架在空间中的角度、角速度等信号;在1节臂安装拉绳式位移传感器,导线挂在4节臂上,实时测量伸缩臂的总长度。

随动液压缸和变幅液压缸的压力测量如图5所示。

图5 随动液压缸和变幅液压缸的压力测量白虚线圈内—变幅液压缸无杆腔压力测点;白实线圈内—变幅液压缸有杆腔压力测点

笔者在随动液压缸和变幅液压缸的无杆腔、有杆腔安装压力传感器,分别测量随动液压缸和变幅液压缸的压力。

数据采集仪如图6所示。

图6 数据采集仪

为了保证测量精度,试验采用Danfoss公司型号为MBS3000的压力传感器,搭配HBM公司eDAQ系列的数据采集仪;将压力传感器连接到伸缩臂叉车臂架系统的液压油路,再将压力传感器的输出线接入数据采集仪;而数据采集仪同时连接控制器局域网络(CAN)总线和笔记本电脑,由笔记本电脑实时输出并保存压力传感器产生的压力信号、CAN总线中的伸缩臂长度信号以及臂架变幅角度信号。

3.3 试验结果与分析

参数τ的优化结果如图7所示。

图7 参数τ的优化结果

由图7可得,当非线性规划求解器迭代到第19次时，RMSE已经达到最小,即找到了全局最优解,表明这时载重估值与载重真值之间的误差已经达到最小;同时，间接表明去噪平滑后的压力信号曲线最逼近原压力信号曲线,吻合程度最好。

经优化后,得到的最优参数τ为91.506。

变幅液压缸的主要参数如表2所示。

表2 变幅液压缸的主要参数

由于篇幅有限,这里仅展示伸缩臂叉车臂架系统中变幅液压缸压力信号的处理。

伸缩臂叉车实时信号如图8所示。

图8 伸缩臂叉车实时信号

从图8(a～c)可以看出:伸缩臂叉车在进行伸缩和变幅的动作时,变幅液压缸压力会因受到惯性冲击、车辆共振以及电磁干扰等因素影响而造成剧烈振荡;

从图8(d)可以看出:对于含有冲击或突变的压力信号,参数优化后的1D TV算法的去噪平滑效果非常好,噪声信号中的高频部分已经完全得到抑制,而且去噪平滑后的信号不失真,波形的总体效应好。

3.4 不同去噪算法的对比分析

EMD类和小波阈值类去噪算法的参数设置如表3所示。

表3 EMD类和小波阈值类去噪算法的参数设置

为验证1D TV算法对于非平稳压力信号实时去噪平滑处理的优势,笔者使用EMD区间阈值(EMD interval thresholding,EMD-IT)和清除迭代EMD区间阈值(clear iterative EMD interval-thresholding,EMD-CIIT)[21]、小波-硬阈值和小波-软阈值算法[22-23]对变幅液压缸压力信号进行处理,并就处理结果进行对比分析(算法中的参数设置详见表3)。

不同去噪算法对变幅液压缸压力信号的处理如图9所示。

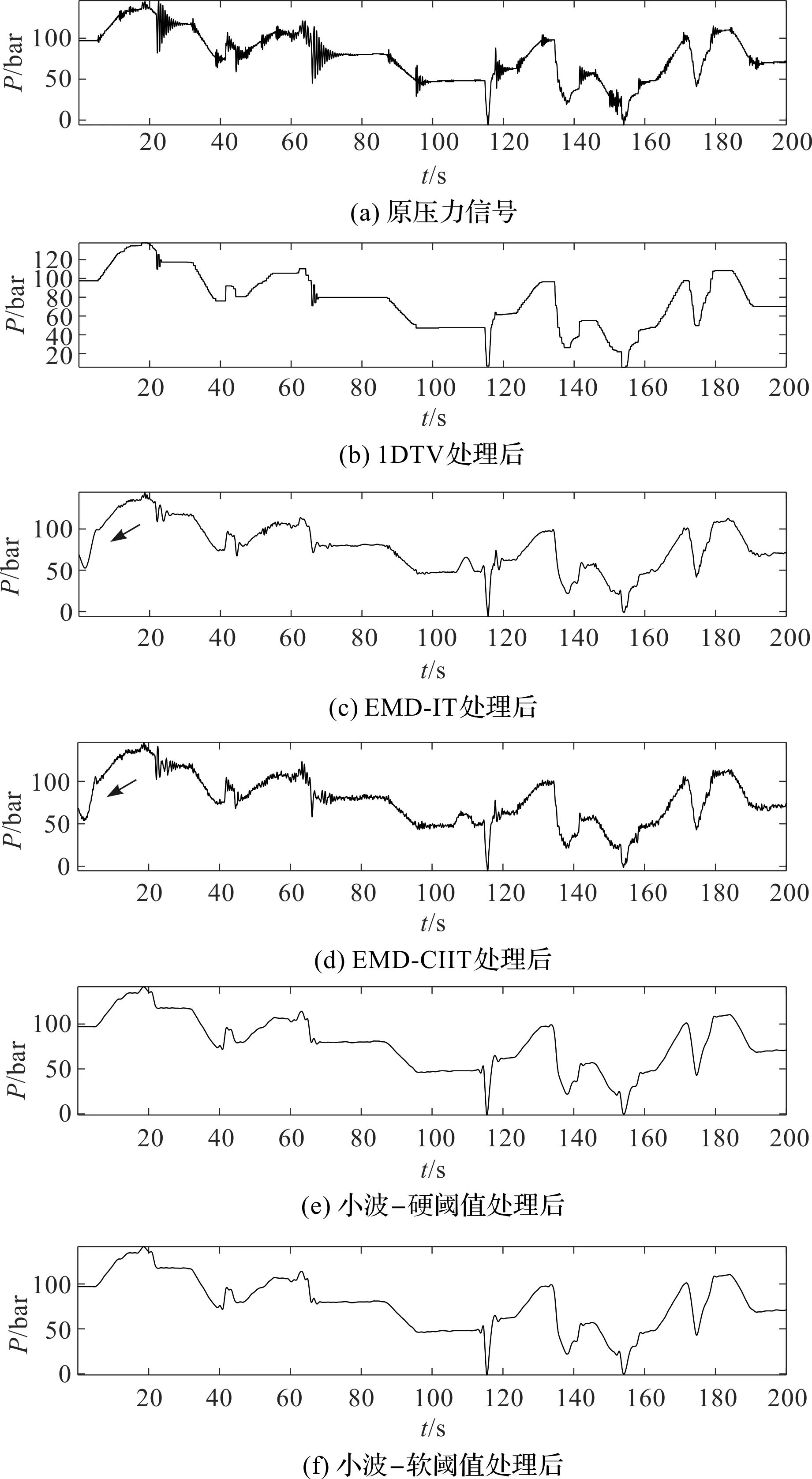
图9 不同去噪算法对变幅液压缸压力信号的处理

从图9(b)可以看出:1DTV算法去噪平滑后的整体波形平滑度和相似度都与原始液压信号非常吻合;

从图9(c,d)可以看出:EMD-CIIT的去噪平滑效果比EMD-IT差,存在较多的高频信号;而且两者都出现了端点效应(图中箭头所示),这是EMD类去噪算法存在的一个弊端[24];

从图9(e,f)可以看出:小波阈值类算法对于液压信号的去噪效果也很好,也能够有效地去除高频信号。

以下实验在MATLAB2019a环境下进行，计算机处理器为英特尔第三代酷睿i5-3320M 2.6 GHz,运行内存为海力士8 GB DDR3L 1 600 MHz。不同去噪算法的性能对比如表4所示。

表4 不同去噪算法的性能对比

为了排除随机性的影响,表4中所有性能指标均为10次去噪平滑后的平均值

从表4中可以看出:

(1)1D TV算法对于液压信号的去噪平滑效果最好,信噪比最高,为27.641 db;互相关系数最大,为0.991 4;在处理时长上的优势特别明显,处理相同的数据时,其仅用时1.3 ms;

(2)EMD-IT和EMD-CIIT算法的去噪平滑效果最差,信噪比最低,互相关系数最小,而且处理时长远大于1D TV算法,但EMD-IT的能力损失最低,为-0.006 5;

(3)小波-硬阈值算法与小波-软阈值算法的去噪平滑效果相同,但小波-软阈值算法处理时长比小波-硬阈值算法的更长,两者都比EMD类去噪算法好,而比1D TV算法差。

文献[25,26]中提到,EMD-IT和EMD-CIIT算法是从第2个IMF开始,利用IMF能量呈线性关系这一特点,而建立了一个去除白噪声模型。再结合图9(c,d)可知,该类算法对于含复杂噪声的非平稳压力信号的去噪平滑效果并不是很好;而且EMD类去噪算法中，IMF的个数会受极值点、插值方式以及筛选终止条件的影响,在分解过程中需要进行迭代,所以其计算效率往往会表现得特别差;与1D TV算法相比,EMD-IT用时147.09 ms,EMD-CIIT用时1 552.5 ms。

小波阈值类算法在设置阈值时,需要给出小波分解后小波系数的长度和噪声的方差,但在实际的复杂工况中,难以对噪声进行计算[27]。

综合算法的性能表现来看:EMD类算法去噪效果不佳,且处理时间长;小波阈值类算法则需要根据先验设定合适的基函数和阈值,从而不能自适应处理非平稳信号,这对于工程车辆数据的实时处理都是非常不利的;而1D TV算法具有计算效率高且去噪平滑效果好的特点,非常适合对工程车辆精确载重估计中的压力数据进行实时处理,能够很大幅度地减小其数据储存成本。

4 结束语

为了解决工程车辆在载重过程中,因受到惯性冲击、工作装置共振以及电磁干扰，造成其液压测量信号的振荡问题,笔者将1D TV算法应用到非平稳性液压信号的去噪中,即先对信号进行平滑处理,再将其输入到载重与变幅液压缸压力、随动液压缸压力有关的载重估计模型中,然后使用MATLAB的fmincon非线性规划求解器,通过最小化载重估值与载重真值之间的均方根误差,优化求解出适用于非平稳液压信号的1D TV算法中的参数;最后进行了实车试验,以及1D TV与EMD-IT、EMD-CIIT、小波-硬阈值、小波-软阈值去噪算法的对比实验。

研究结论如下:

(1)经参数优化后的1D TV算法能够有效实时地处理因受惯性冲击、车辆共振以及电磁干扰等因素影响而造成剧烈振荡的非平稳性液压信号,而且去噪平滑效果很有效;

(2)从去噪平滑效果来看,1D TV算法相比于EMD-IT、EMD-CIIT、小波-硬阈值以及小波-软阈值算法,信噪比分别提高了5.154 6 db、5.096 4 db、0.653 db、0.653 db;

(3)1D TV算法计算效率优势明显,是EMD-IT算法计算效率的113倍,EMD-CIIT算法计算效率的1 194倍,小波-硬阈值算法计算效率的11倍,小波-软阈值算法计算效率的15倍,体现了其具有快速、非迭代以及逐点扫描等优势特点;

(4)相比于EMD类和小波阈值类去噪算法,1D TV算法更适合于对工程车辆精确载重估计中非平稳液压信号进行实时处理。

但是1D TV算法中的参数是通过试验和优化来进行选取的,因此,在后续的工作中,笔者还需要对如何自适应地选择参数做进一步的研究。