插装阀压力飞升速率的影响因素研究*

黄 浩,陈义训,金晓宏,何志鹏

(武汉科技大学 机械自动化学院,湖北 武汉 430081)

0 引 言

在大流量、高压力的电液控制场合,二通插装阀的应用较为普遍。二通插装阀具有阀芯动作灵敏、抗堵塞能力强、密封性好、泄漏小、油液流经阀口压力损失小等特点。

二通插装阀的压力飞升速率影响插装阀的开启与关闭特性,进而影响整个插装阀系统的响应特性。因此,一些研究人员对二通插装阀的压力飞升速率进行了相应的研究。

为了更好地对液压系统进行优化设计,进而提高液压系统的稳定性、可靠性,有必要对液压系统中的插装阀各个方面的影响因素进行相关分析和研究。

庹前进等人[1]研究了插装阀方向元件在阻尼孔位置、腔室的面积差等方面对插装阀动作特性的影响,但是他们未对其中的阻尼孔的直径与长度进行研究。

在对二通插装阀系统动态特性进行的仿真研究中,董敏等人[2]利用键合图方法,对插装阀的启闭特性进行了仿真,验证了插装阀启闭的有效性,该研究较好地对插装阀的启闭特性进行了仿真。贾文华等人[3]采用AMESim对换向阀进行了联合仿真,并运用了相关软件,对相应的V型节流槽进行了优化设计;但是该研究未进行与插装阀的联合体仿真,未研究换向时间对插装阀启闭特性的具体影响。张欣[4]采用了不同的控制方式,对插装阀的启闭特性进行了分析,研究了不同控制方式对插装阀特性的具体影响。王欣等人[5]采用功率键方法,对插装阀进行了优化设计研究,对插装阀的动态特性进行了分析;但是他们未就阻尼孔的替代方面进行研究。

综上所述,在插装阀阻尼孔的位置和启闭特性等的研究方面目前已经有了不少较好的成果,但是关于阻尼孔长度和阻尼孔替代的仿真研究仍然较少。

因此,笔者以试验台系统中的插装阀为研究对象,从插装阀的结构与压力飞升的标准入手,利用AMESim仿真软件建立插装阀模型,就管道的长度、压力与流量等级,阻尼孔的直径、阻尼孔的替代和先导阀换向时间等因素,对压力飞升速率的影响进行研究。

1 插装阀的结构及飞升标准

1.1 插装阀的结构

试验台采用的某型二通插装阀的公称直径为32 mm。笔者根据实际工况选用型号为LC32A40E6XB的二通插装阀。二通插装阀由大结构先导控制阀、控制盖板、插装件、插装块等组成。

二通插装阀内部结构包括阀套、阀芯、弹簧、密封圈等,如图1所示。

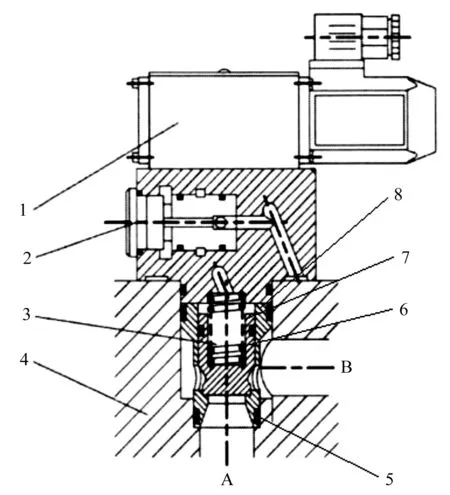
图1 插装阀组成图1—先导控制阀;2—控制盖板;3—插装件;4—插装块体;5—密封圈;6—弹簧;7—阀芯;8—阀套

图1中,先导控制阀为二位四通电磁换向阀。

单位时间的压力飞升速度公式如下:

(1)

式中:ΔP—在ΔT时间内容腔的压力变化值,MPa;Δq—在ΔT时间内进出容腔流量差,m3/s;Ke—油液的体积弹性模量,MPa;V—被试阀与阶跃加载阀之间的油路连通容积,m3;v—在ΔT时间内进出容腔的压力变化率,MPa/s。

根据插装阀开启与闭合受力分析,插装阀阀芯的力平衡方程如下:

F=PAAA+PBAB-PCAC-k(x-x0)

(2)

式中:AA—油口A的有效工作面积,m2;AB—油口B的有效工作面积,m2;AC—油口C的有效工作面积,m2;PA—油口A的压力,MPa;PB—油口B的压力,MPa;PC—油口C的压力,MPa;k—弹簧刚度,N/m;x—弹簧预压缩量,m;x0—位移,m。

由式(2)可得,当F>0时,阀口开启;当F<0时,阀口闭合。

笔者对所选用插装阀的阀芯进行受力分析,得到阀芯的运动方程如下:

(3)

式中:m—阀芯质量,kg;B—芯运动粘性阻尼系数,N/(m·s-1);Ks—态液动力系数。

其中:Ks=CdCvπdsin2β。

1.2 压力飞升速率的标准

在瞬态工况标准中,压力飞升速率试验有如下标准:

(1)被试阀进口压力变化率在600 MPa/s～800 MPa/s范围内达到B级要求,如表1所示。

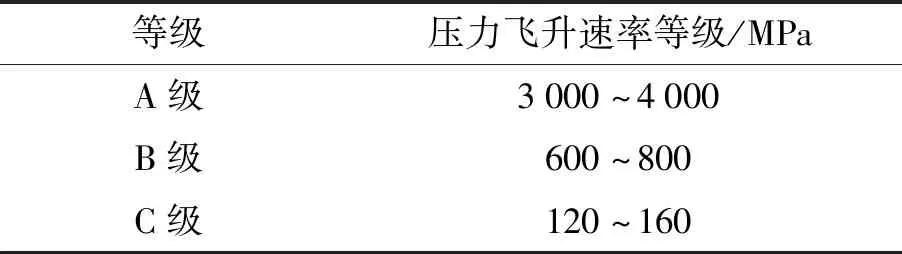
表1 压力飞升速率等级

其中,进口压力变化率是指进口压力从最终稳态压力值与起始压力值之差的10%上升到90%的压力变化量与相应的时间之比[6];

(2)阶跃加载阀动作时间不应超过被试阀相应时间的10%,或者最大不应超过10 ms;

(3)进行瞬态实验时,加载的压力阶跃信号可以使得被试阀的进油口产生一个满足瞬态条件的压力梯度。

2 压力飞升速率的影响因素

影响压力飞升速率的因素主要有:液压管路的长度与混入气体、先导换向阀的换向时间、阻尼孔直径与替代、压力与流量等级等。

2.1 混入气体与管路长度

体积弹性模量公式如下:

(4)

式中:Vo—压力变化前的体积;dV—在dp的作用下液体体积变化值;dp—压力变化值。

油液的工作时间内会出现体积变化,即:

(5)

式中:Km—有效的体积弹性模量;KG—气体的体积弹性模量;Kf—纯液体的体积弹性模量;Kc—管道形成的体积弹性模量;VG—混入气体的体积;Vf—纯液体的体积;Vt—气体与液体的总体积,Vt=VG+Vf。

油液工作时,会出现体积随着压力的变化而变化的现象;同时,油液也会不可避免地接触空气,进而使空气进入油液当中,影响压力飞升速率,甚至是整体系统[7-9];

溶解在液压油中、以微小的气泡悬浮在油液中可能是油液中气体存在的两种形态。这些以不同的形态存在于油液中的气体,不单单是形成气蚀的重要原因,还是干扰压力飞升速率的重要因素[10-12];

在强烈干扰的影响下,油液中的气体会不断析出,从而增加油液的体积,进而减低油液的有效体积弹性模量,最终影响飞升速率。

2.2 先导换向阀换向时间

先导换向阀的作用是控制二通插装阀控制油路的开闭。因此,它能够影响二通插装阀开闭时间和电磁换向阀的换向时间;并且换向时间能够影响单位时间内进入插装阀控制腔的油液流量,从而影响飞升速度。

2.3 阻尼孔

由于插装阀的先导换向阀和控制油口所需的流量较小,主系统的流量较大,因此笔者在插装阀的控制油口设置阻尼孔,在主系统与先导换向阀之间设置阻尼孔。如果阻尼孔较大,可能会损坏插装阀;如果直径较小,可能会影响插装阀的启闭时间[13]。

2.4 压力等级与流量等级

在标准的瞬态试验当中,测试阀的压力被称为公称压力,经过测试阀的流量被称为公称流量。不同压力等级与流量等级的阀体在进行瞬态试验期间,系统的压力与流量也会不一样[14-18]。

因此,需要对不同系统中的压力和流量进行具体分析,研究两者在瞬态试验中对压力飞升速率的影响。

3 AMESim仿真及结果分析

笔者使用AMESim中的液压库对新的快速切换单元阶跃加载原理图进行仿真[19-21]。在一般情况下,需要对子模型进行确定,但这样容易出错,故此处对该仿真进行手动子模型设置;而其中采用的试验参数,均来自实验元器件的真实参数。

AMESim仿真的流程图如图2所示。

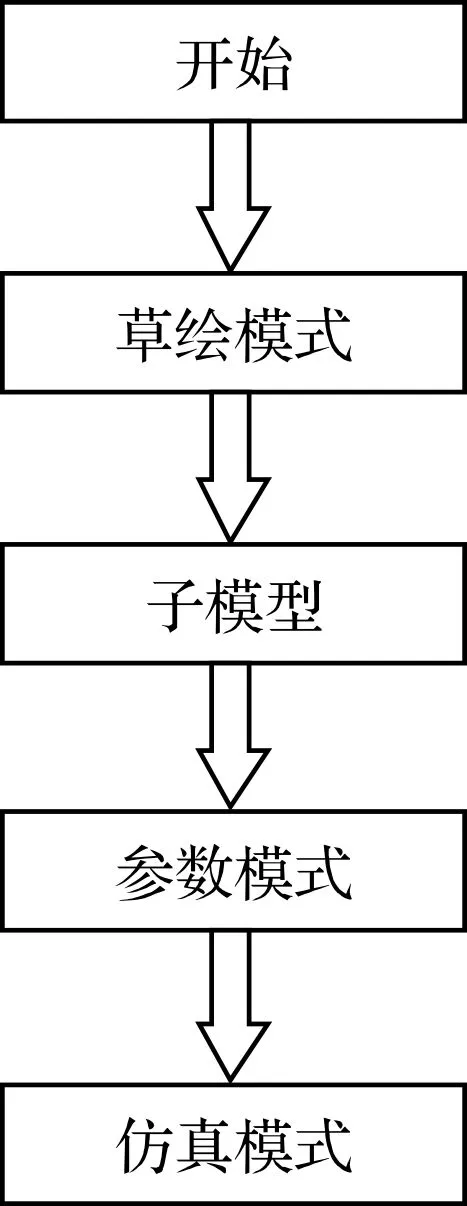
图2 AMESim仿真流程图

图2的流程图说明如下:

(1)开始。按照试验方案,建立瞬态试验的原理图;

(2)草绘模式。草图链接,在仿真软件的HCD库中进行建模;

(3)子模型。手动建立子模型(一般情况下使用默认子模型);

(4)参数模式。对各元件进行参数设置;

(5)仿真模式。设置好仿真时间,运行、绘制相应的结果图,并进行后处理[22]。

带阻尼孔的AMESim模型如图3所示。

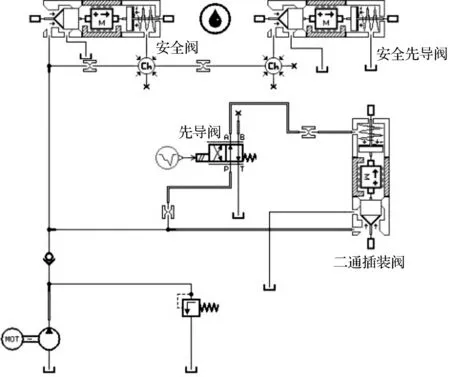
图3 带阻尼孔AMESim模型

不带阻尼孔采用软管AMESim模型如图4所示。

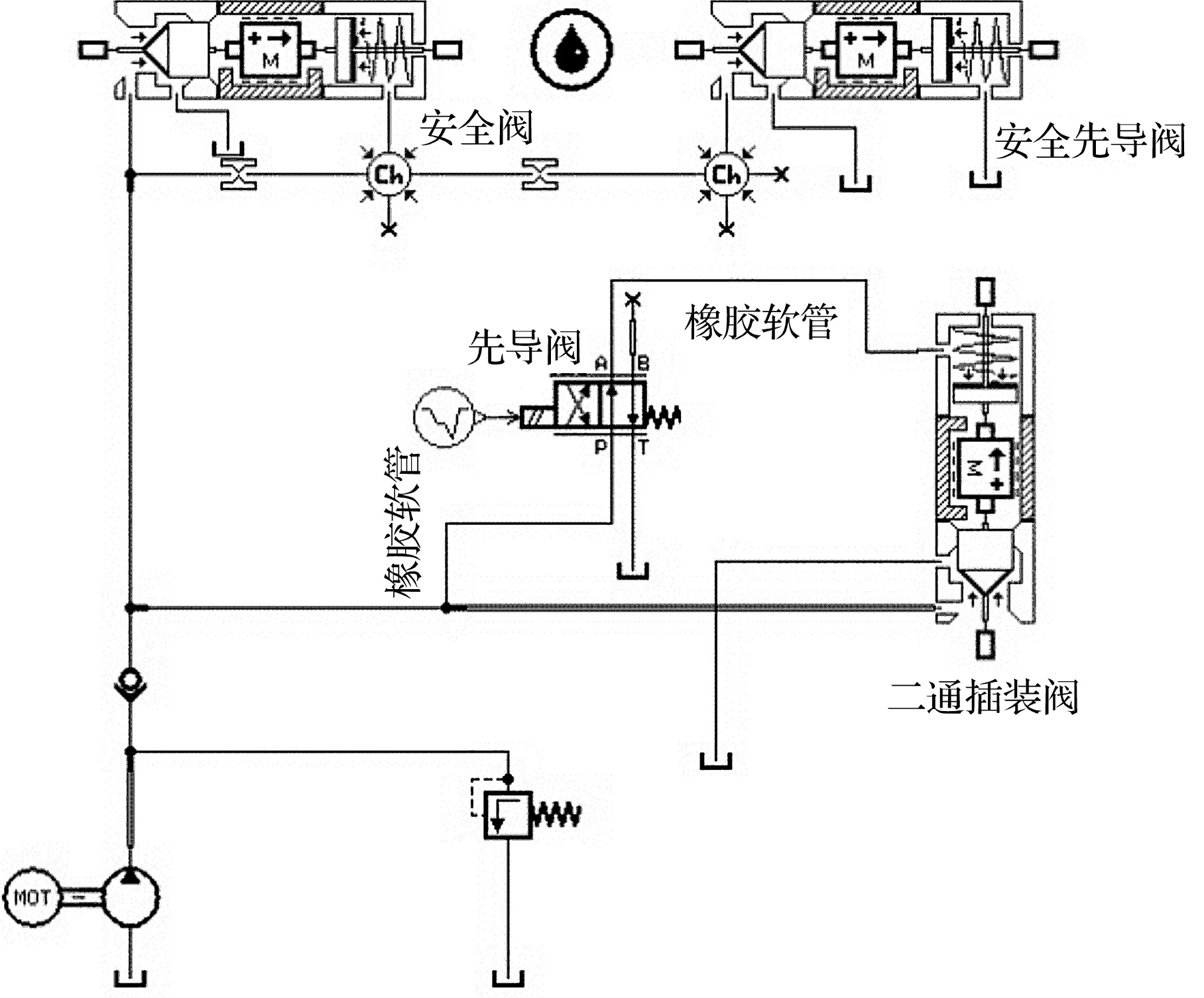
图4 不带阻尼孔采用软管AMESim模型

实验阀体仿真模型的具体参数设置如表2所示。

表2 实验阀体仿真模型的具体参数

在建立的插装阀仿真模型中,会对压力飞升速率产生影响的因素主要包括阻尼孔、先导阀的换向时间、流量、压力等[23]。

该仿真主要集中在插装阀与先导阀的组合体上,将先导阀看作单一的节流阀,去除相应的阻尼孔,用橡胶软管代替(其中,橡胶软管的阻尼系数一般维持在0.45左右),获得去除阻尼孔前后的压力飞升时间及速率。

插装阀实验基本参数如表3所示。

续表

经笔者查阅相关手册,得到表3中采用的相关参数如下:

采用的LC32A40E6XB二通插装阀的A口面积AA=5.3 cm2,B口面积AB=2.74 cm2,C口面积AC=8.04 cm2;阀芯最大开口xmax=9 mm,阀芯质量m=0.05 kg,半锥角β=45°,节流孔直径为2 mm,先导换向阀的通径为6 mm。

根据式(3),可以得到等效阻尼孔直径R=1.68 mm,Ks=CdCvπdsin2β=4.88×10-2。

3.1 混入气体与管路长度

在上述仿真模型中,笔者设置的管道长度分别为2 m、4 m、6 m、8 m、10 m,且设置的相关数据如下:换向阀的换向时间为8 ms、控制油口的阻尼孔直径为2 mm、系统的流量为100 L/min。

最终得到的仿真结果,即不同管道长度的瞬态响应曲线,如图5所示。

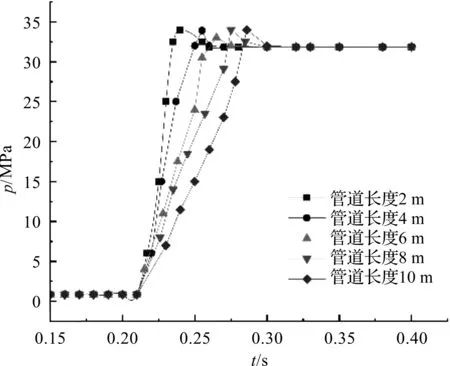
图5 不同管道长度的瞬态响应曲线

由图5可知:管道长度越短,压力飞升的速率就越大;同时,可以获得不同管道长度时,压力从稳态压力值的10%上升到90%所需的时间;根据式(1)便可以获得不同的管道对应的压力飞升速率。

不同管道长度的压力飞升速率如表4所示。

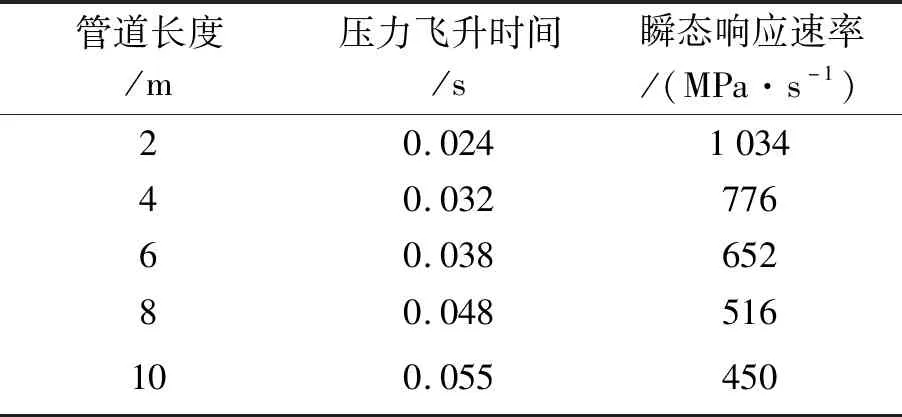
表4 不同管道长度的压力飞升速率

管道长度的仿真试验方案为:在其他因素不改变的情况下,随着管道长度增加,压力飞升速率不断降低;当达到6 m以上时,则不再符合相关标准。

3.2 先导换向阀换向时间

在仿真设置中,先导换向阀的换向时间分别为10 ms、30 ms、60 ms、100 ms、160 ms;相关的数据如下:阻尼孔直径为2 mm,主泵出口与安全阀之间的管道长度为3 m,系统的流量设置为100 L/min。

最终得到的仿真结果,即不同换向时间的瞬态响应曲线,如图6所示。

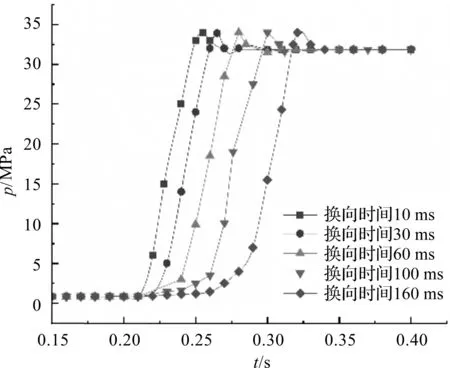
图6 不同换向时间的瞬态响应曲线

在换向时间较短的情况下,压力飞升的速率会加快;同时,可以得到不同换向时间时,压力从稳态压力值的10%上升到90%所需的时间;根据式(1)便可以获得不同的换向时间对应的压力飞升速率。

不同换向时间的压力飞升速率如表5所示。

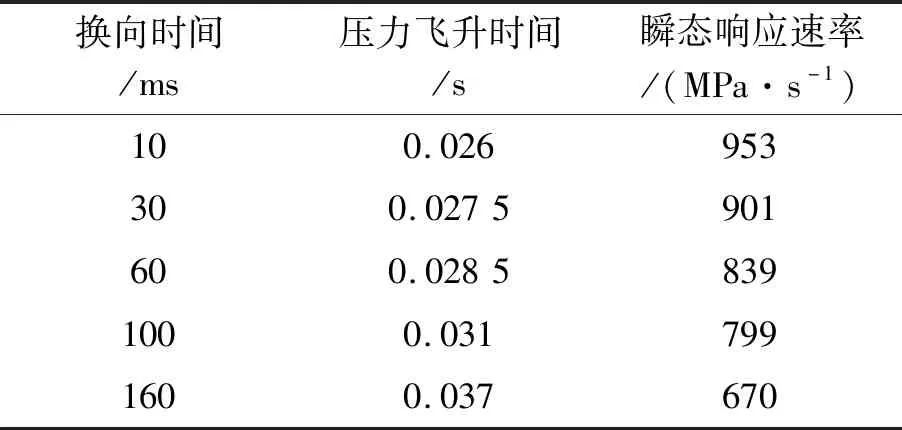
表5 不同换向时间的压力飞升速率

换向阀换向时间发热仿真试验方案为:在其他因素不变的情况下,随着先导控制阀的换向时间不断延长,压力飞升速率出现降低。

3.3 阻尼孔直径与阻尼孔替代

笔者设置阻尼孔的直径分别为1.5 mm、2.0 mm、2.5 mm、3.0 mm,且暂时设置先导换向阀的换向时间为10 ms,主泵出口与安全阀之间的管道长度为3 m,系统流量为100 L/min。

最终得到的仿真结果,即不同阻尼孔直径的瞬态响应曲线,如图7所示。

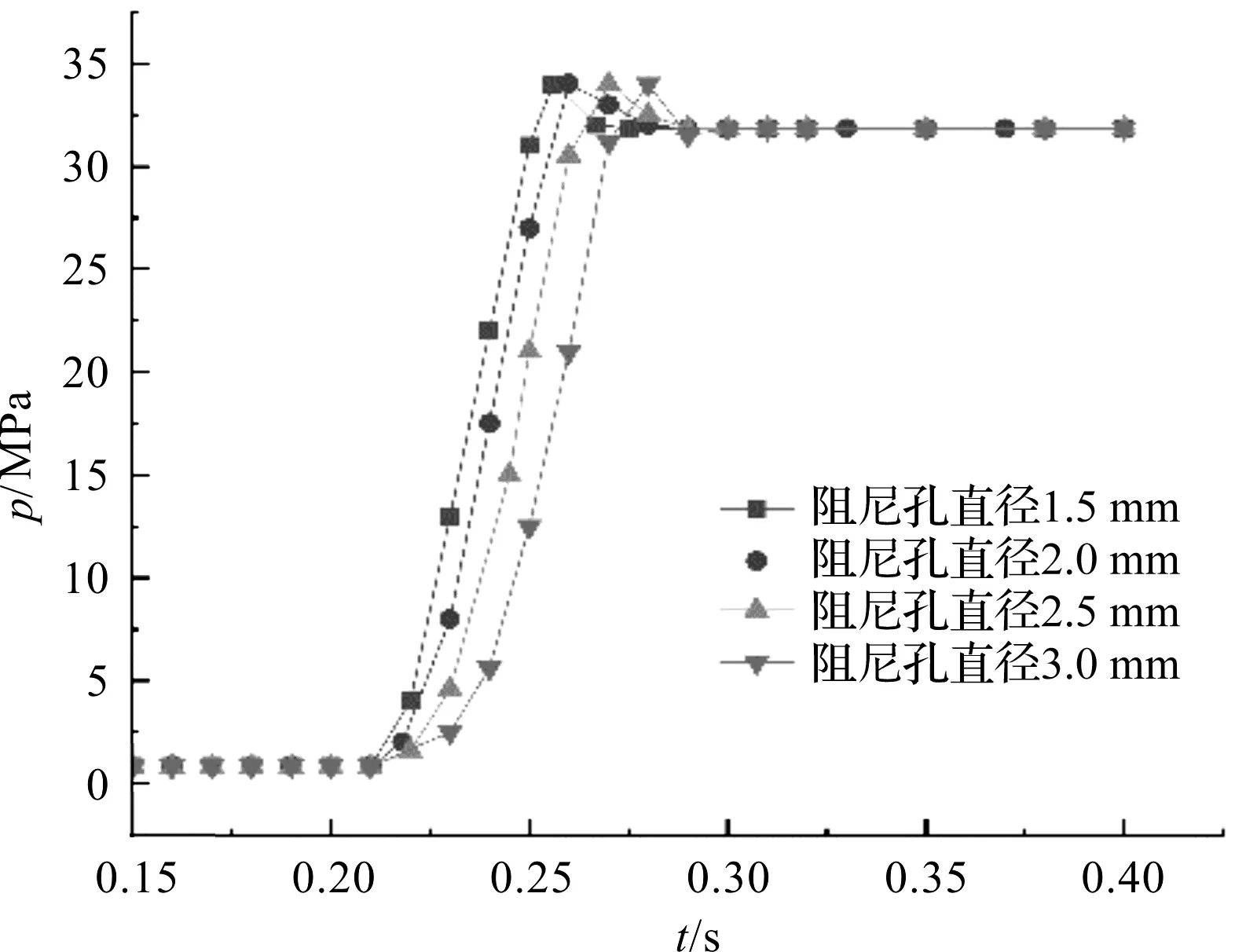
图7 不同阻尼孔直径的瞬态响应曲线

图7中,阻尼孔的直径越大,压力飞升的速率就越大,同时可以得到不同阻尼孔直径时,压力从稳态压力值的10%上升到90%所需的时间;根据式(1)可以获得不同阻尼孔直径时的压力飞升速率。

不同阻尼孔直径的压力飞升速率如表6所示。

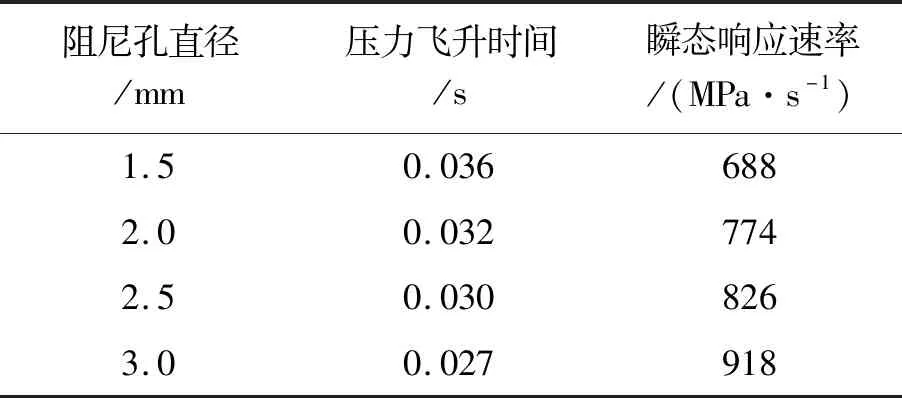
表6 不同阻尼孔直径的压力飞升速率

笔者设置所采用阻尼孔的直径为2.0 mm,且暂时设置先导换向阀的换向时间为10 ms,主泵出口与安全阀之间的管道长度为3 m,系统流量为100 L/min,得到仿真结果。

其中,带有阻尼孔的模型设置详见图3,用橡胶软管代替的模型设置详见图4。

阻尼孔的代替方案为:用橡胶软管代替阻尼孔,仿真分析中压力飞升速率加快。

3.4 压力等级与流量等级

笔者设置系统的压力为32 MPa,设置系统流量分别为40 L/min、60 L/min、100 L/min、160 L/min、300 L/min,并得到相应的仿真结果。

当系统的压力为32 MPa时,在流量增大的同时,瞬态试验压力飞升的速率就越大。

不同流量等级的压力飞升速率如表7所示。

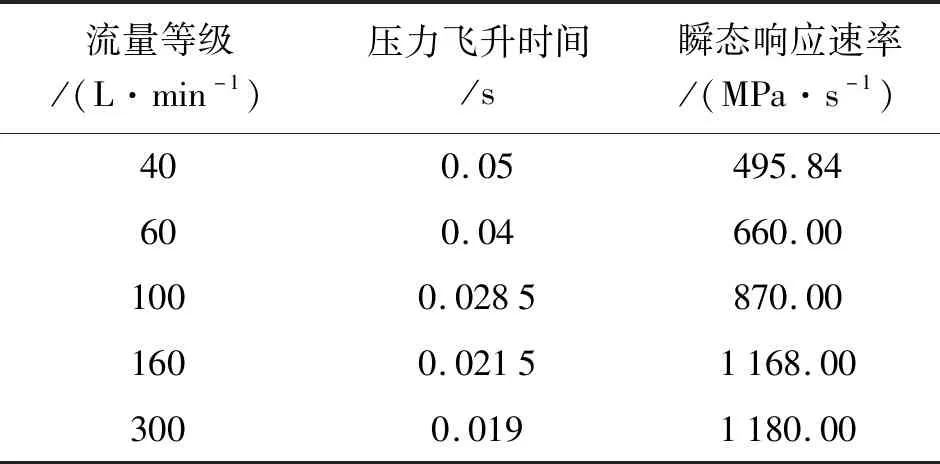
表7 不同流量等级的压力飞升速率

笔者设置系统流量为100 L/min,分别设置系统流量为16 MPa、20 MPa、24 MPa、32 MPa,得到仿真结果。

当系统的流量为100 L/min时,系统压力增大的同时,影响油液的相关因素会影响或者提高压力飞升

的速率;但是系统压力提高,系统的泄漏量也会增大,不利于压力飞升速率的增加。

不同压力等级的压力飞升速率如表8所示。

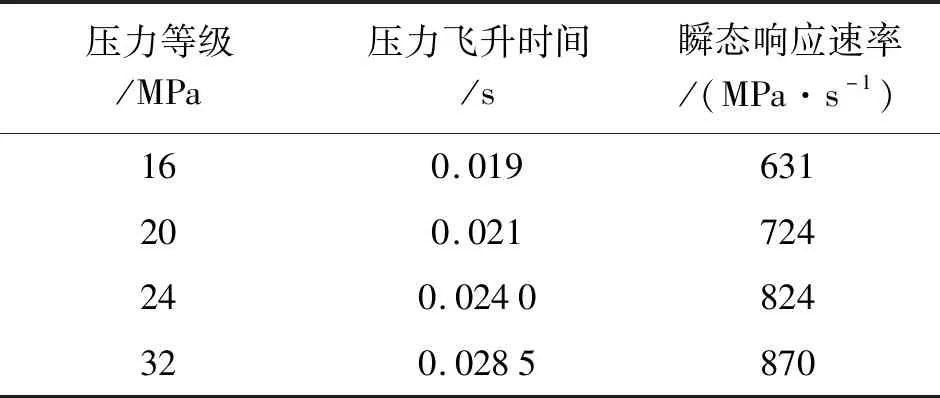
表8 不同压力等级的压力飞升速率

不同压力等级和流量等级瞬态响应变化图,如图8所示。

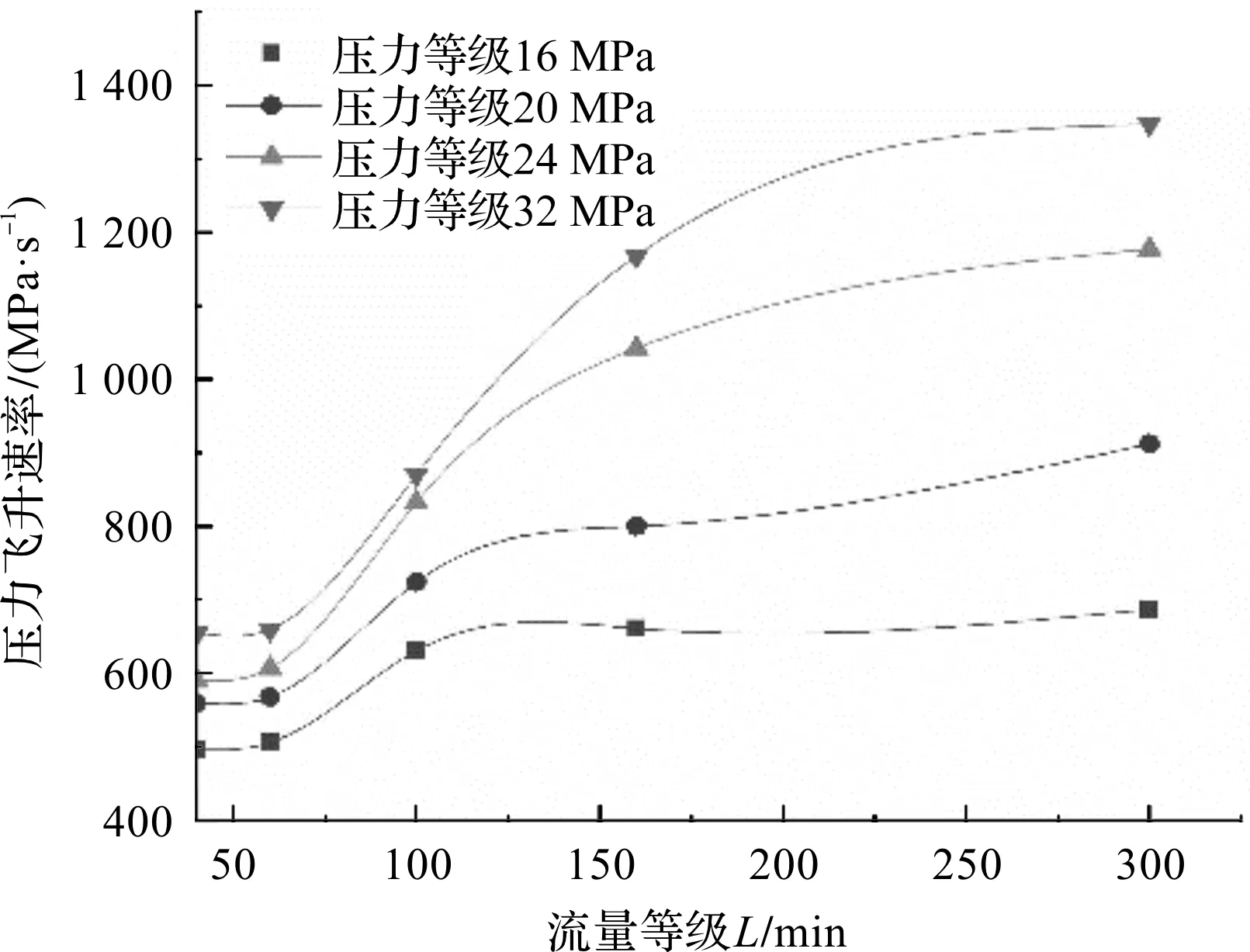
图8 不同压力等级和流量等级瞬态响应变化图

4 瞬态实验及结果分析

根据上述仿真结果,笔者选用二通插装阀的型号为LC32A40E6XB,过渡盖板的型号为LFA32-WEA6XB,先导换向阀的型号为G02-B2-D24-20,分别进行瞬态实验。

实验总体装置图及插装阀等的实物图如图9所示。

图9 总体装置图及插装阀等的实物图

具体的试验步骤为:

(1)额定压力为16 MPa,额定流量为100 L/min;

(2)额定压力为32 MPa,额定流量为160 L/min。

实验结果如图10所示。

由图10可知:实验结果为缩小倍数的结果图,皆达到实验要求。

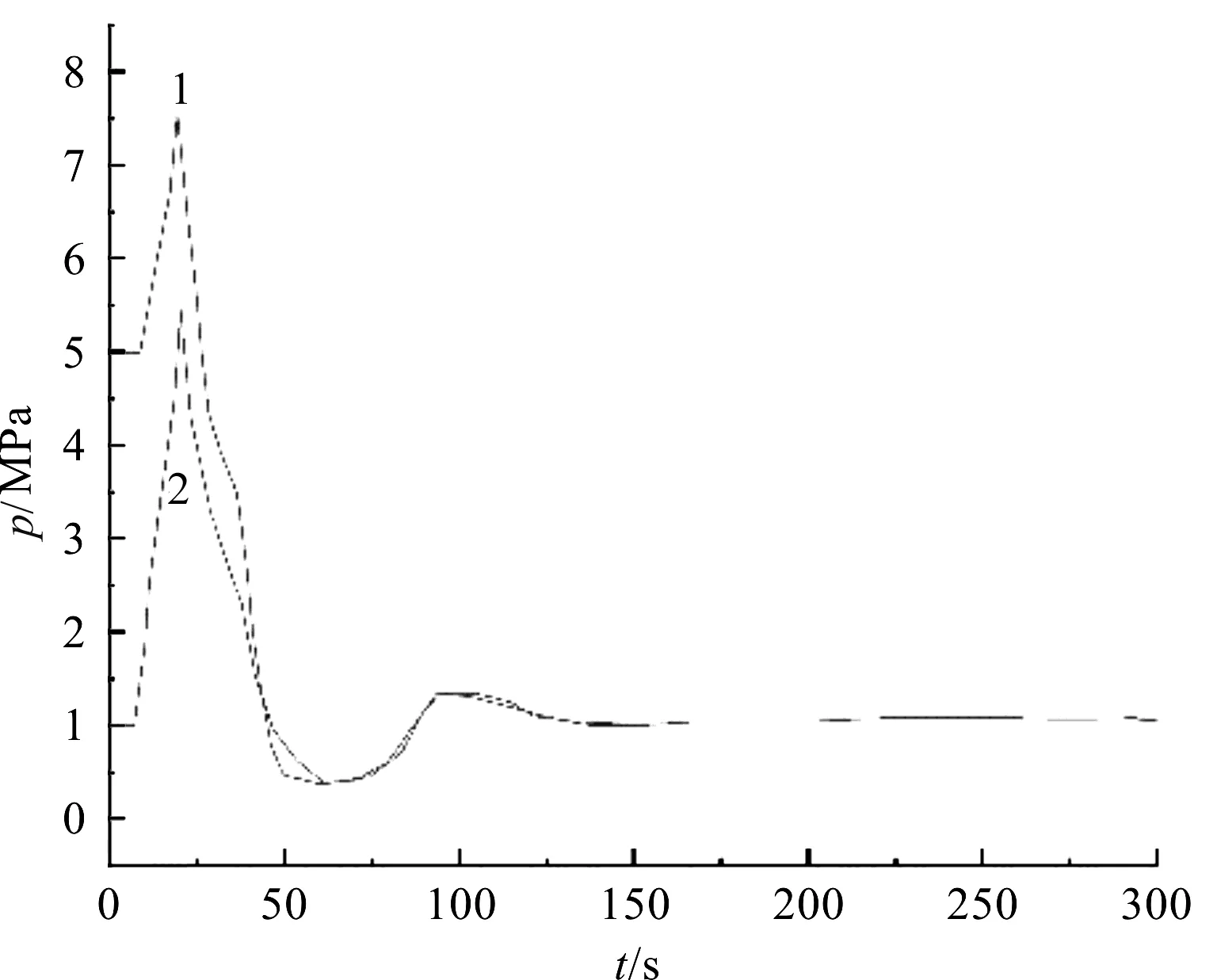
图10 实验结果图1—工况为采用额定压力为16 MPa,额定流量为100 L/min;2—工况为采用额定压力为32 MPa,额定流量为160 L/min

(1)额定压力为16 MPa,额定流量为100 L/min时,压力从稳态压力值的10%上升到90%所需的时间ΔT为0.018 s,因此压力飞升速率为:

(6)

(2)额定压力为20 MPa,流量为160 L/min时,压力从稳态压力值的10%上升到90%所需时间ΔT为0.019 s,获得的压力飞升的速率为:

(7)

上述两次试验压力飞升的速率分别为675.5 MPa/s和808.4 MPa/s,由此可见,以上结果符合瞬态实验的B级要求。

5 结束语

笔者通过对插装阀的结构以及压力飞升相关标准进行研究,分析了压力飞升的影响因素,通过仿真和基础数据的运用,得到了相应插装阀压力飞升影响因素的影响结果,并进行了实验,验证了相关的飞升要求。

研究结果表明:

(1)混入气体与管路材料对压力飞升速率的影响:气体的渗入改变了油液的体积,影响了弹性模量,进而影响压力飞升的速率。所选管路的长度和直径越大,则管路中的油液体积越大,当压力发生变化时,体积量的变化越大,对体积弹性模量的影响越大,进而影响压力飞升速率;

(2)先导换向阀换向时间对压力飞升速率的影响:在达到相关标准的前提下,换向的时间越短,压力飞升的速率越快;

(3)阻尼孔直径与有无对压力飞升速率的影响:阻尼孔直径越小,进入插装阀控制油口的流量较小,会影响插装阀的启闭时间,加快压力飞升的速率。在没有阻尼孔的情况下,用橡胶软管代替阻尼孔,可加快压力飞升速率;

(4)压力等级与流量等级对压力飞升速率的影响:在相同的系统压力下,系统流量越大,压力飞升的速率越快;在相同的系统流量下,系统压力的提升对压力飞升的速率影响不大;

(5)进行了瞬态试验,得到了相应的瞬态试验响应数据;为了达到B级精度要求,研究了阻尼孔直径与阻尼孔代替等参数对压力飞升速率的影响,确定了一组可以达到精度要求的参数,并最终通过实验验证了其准确性与可行性。

根据上述理论分析可知,在设计插装阀系统时,应根据实际工况,选择密封较为严密的管路;换向阀要选择适合实际工况,并且换向时间较短的元件;要在保证安全的前提下替代阻尼孔,并选用合适的压力流量等级。

在下一研究阶段,笔者将会对插装阀其他方面的影响因素做进一步的研究。