基于状态观测器的四旋翼无人机轨迹跟踪控制
熊志豪, 邓 涛, 郑宇惟, 周 鑫, 吴玉泽
(1.重庆交通大学,a.机电与车辆工程学院; b.航空学院,重庆 400000; c.绿色航空技术研究院,重庆 401000;2.绿色航空能源动力重庆市重点实验室,重庆 401000)
0 引言
近年来,随着微处理器、传感器等电子元件的小型化以及生产成本的不断降低,小型无人机的发展得到了越来越多的关注和研究。其中,四旋翼无人机凭借结构简单、可悬停以及机动性强等优势在环境监测、基础设施监管、军事侦察、航空摄影、农业植保等领域得到了广泛的应用[1]。
为保证四旋翼无人机按计划完成指定任务,需要对其进行高精度的轨迹跟踪控制。然而,四旋翼无人机具有非线性、欠驱动、强耦合、多变量等特性,并且容易受到地面效应、阵风等外界干扰的影响,使得高品质飞行控制器的设计与实现面临较大的挑战。针对四旋翼无人机的飞行控制问题,已有许多学者使用不同的控制方法进行了大量的研究,如线性二次调节器[2]、反步控制[3]、模型预测控制[4]、自适应控制[5]、滑模控制[6]等。尽管以上方法能在一定程度上改善四旋翼无人机的飞行性能,但仍然存在对系统模型的精度要求高、对系统未建模动态的适应性不强、工程实践性较差或者在仿真时未考虑电机的动态特性、对四旋翼无人机的姿态角进行了小扰动假设等问题。
对此,本文提出一种基于状态观测器的全局快速终端滑模控制算法应用于四旋翼无人机的轨迹跟踪控制。其中,全局快速终端滑模控制引入了带有非线性函数的终端滑模面,使得系统的跟踪误差能够在有限时间内收敛,并且其控制律中不含有不连续的切换项,从而能够避免抖振现象的发生;扩张状态观测器可以实时观测系统的“总扰动”并在线补偿,以观测器的估计值来替代控制律中的系统模型信息以及传感器的线速度和角速度信号,可以有效地增强控制器对四旋翼无人机模型不确定性以及外部干扰的鲁棒性能。最后,本文通过对系统稳定性的分析以及数值仿真结果验证了所提控制算法的有效性。
1 四旋翼无人机模型建立
本文选取的研究对象为“X”型结构的四旋翼无人机,即机头与机架之间的夹角为45°。为了描述四旋翼无人机的姿态和位置,需要建立与地球中心固连的地球坐标系(oexeyeze)和与四旋翼无人机固连的机体坐标系(obxbybzb),如图1所示。
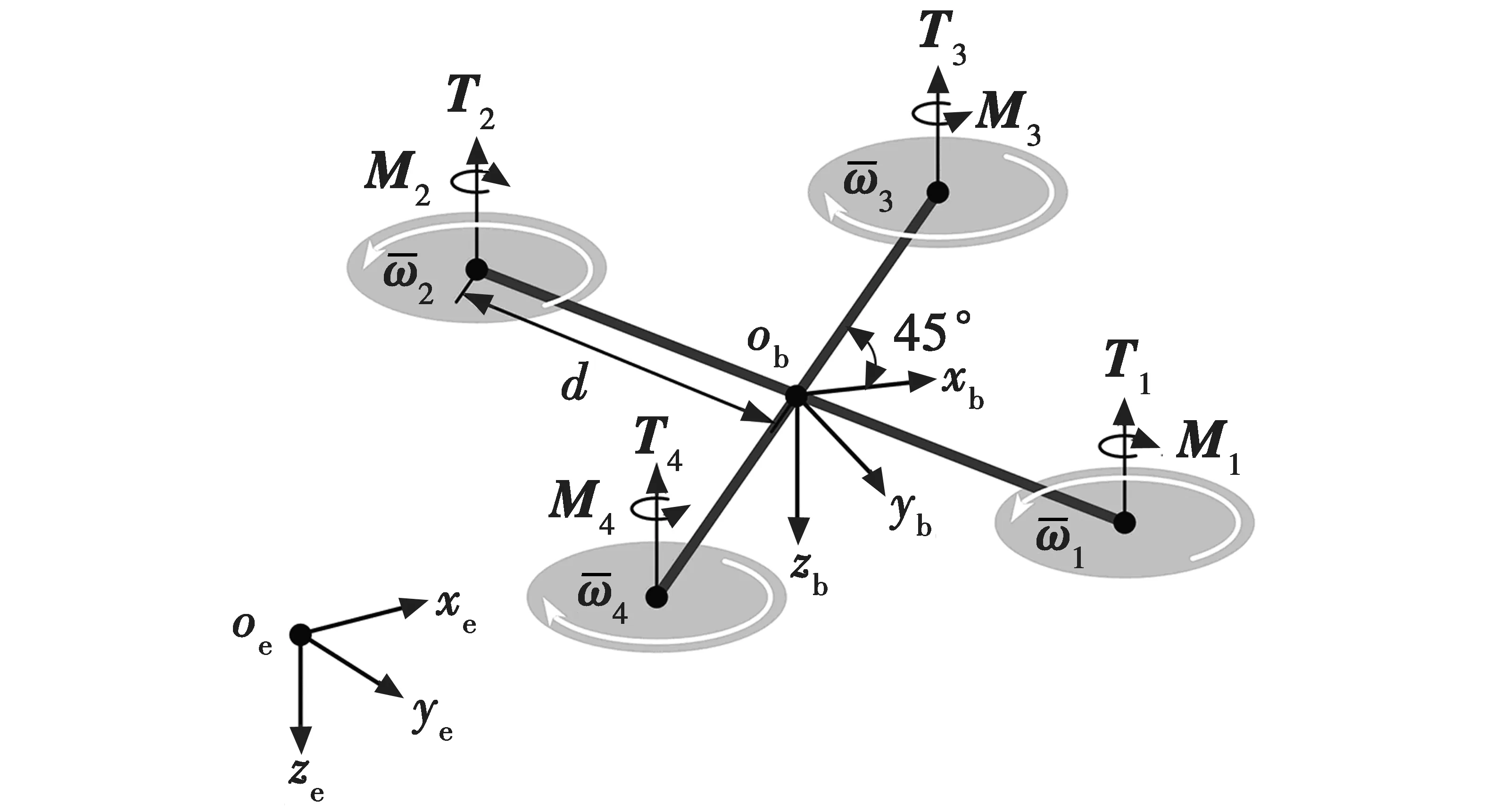
图1 四旋翼无人机的结构及坐标系

假设1 四旋翼无人机是均匀对称的刚体。
假设2 四旋翼无人机的质量和转动惯量为常量。
假设3 四旋翼无人机的几何中心即其重心。
1.1 动力学及运动学模型
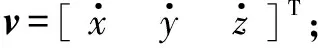
(1)
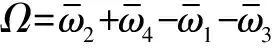
1.2 控制效率模型
控制效率模型描述的是四旋翼无人机在螺旋桨转速输入下产生的拉力和力矩。对于“X”型结构的四旋翼无人机,螺旋桨旋转产生的总拉力f和总力矩τ与螺旋桨转速的关系可表示为
(2)
式中:cT为螺旋桨拉力系数;CM为螺旋桨扭矩系数。
1.3 电机模型
一般情况下,四旋翼无人机所使用的无刷直流电机的动态响应过程可以简化为一阶系统,其传递函数可表示为
(3)
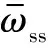
2 控制器设计
本文采用的控制策略是由位置控制器和姿态控制器串联而成的两级串级控制器结构,外环为位置控制器,内环为姿态控制器。其中,外环位置控制器的输入为期望轨迹Pd=[xdydzd]T,输出为期望拉力fd以及期望的滚转角φd和俯仰角θd;内环姿态控制器的输入为φd,θd以及期望的偏航角ψd,输出为期望的力矩τd=[τxdτydτzd]T。接下来基于扩张状态观测器以及全局快速终端滑模控制算法对四旋翼无人机的轨迹跟踪控制器进行设计,控制结构如图2所示。

图2 四旋翼无人机串级控制结构
2.1 扩张状态观测器设计
以滚转角通道为例设计扩张状态观测器,其余通道的设计方法类似。假设四旋翼无人机的俯仰角和滚转角都很小,根据式(1),滚转角φ的微分方程可表示为
(4)

(5)

利用式(5)系统的输入输出数据,可设计三阶线性ESO在线估计系统状态变量[8],即
(6)
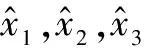
(7)
式中,ωo为观测器带宽。
2.2 位置控制器设计
位置控制可分为高度控制通道和水平控制通道两个通道。位置系统状态方程可表示为
(8)
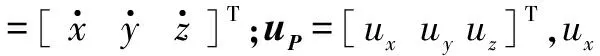
(9)
以水平通道x为例,定义水平位置跟踪误差
ex=xd-x
(10)
设计全局快速终端滑动模态为[10]
(11)
式中:α0,β0∈R+;p0>q0>0,且都为奇数。基于ESO的滑模控制律为
(12)
同理可得水平通道y以及高度通道z的虚拟控制律为
(13)
(14)
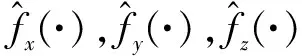
(15)
由式(9)可以反解出期望的总拉力fd、期望的滚转角φd以及期望的俯仰角θd分别为
(16)
(17)
(18)
2.3 姿态控制器设计
姿态控制通道的控制信号指令来源于位置控制器输出的期望滚转角φd和期望俯仰角θd,以及期望偏航角ψd。根据式(12)可得姿态控制通道的控制律为

(19)

(20)
3 稳定性分析
本章以姿态控制器中滚转角φ的控制回路为例对闭环控制系统的稳定性进行分析,其余通道的稳定性分析过程与其类似。首先应保证滚转角控制回路中扩张状态观测器观测系统状态的速度足够快,之后再根据闭环系统的Lyapunov函数来证明滚转角控制回路的稳定性。
定理1存在足够大的观测器带宽ωo,使得对式(4)被控对象所构建的式(6)线性扩张状态观测器的观测误差是渐近收敛的。

定理2由式(4)被控对象、式(6)ESO以及式(19)控制器组成的闭环系统稳定。
证明 取闭环系统的Lyapunov函数为
V=Vs+Vo
(21)
式中,Vs,Vo分别表示滚转角控制器和观测器的Lyapunov函数。选取控制器的Lyapunov函数为
(22)
根据式(11)全局快速终端滑动模态可得
(23)
将滚转角微分方程式(4)以及式(19)滚转角通道的控制律代入可得
(24)
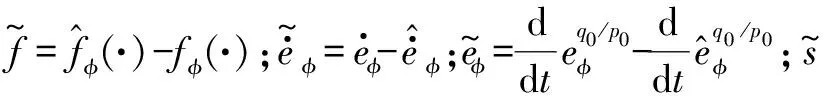
(25)
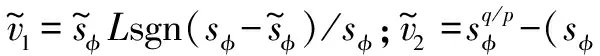
(26)
则有
(27)
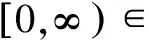

(28)
式中,α为任意常数。
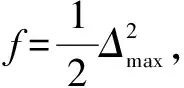
(29)
取φ>1/2,则有
(30)
由式(30)可知,系统跟踪误差有界,且随着φ取值的增大而减小。
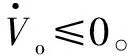
4 仿真分析
为验证本文提出的控制策略在四旋翼无人机轨迹跟踪控制中的有效性,在Matlab/Simulink环境下对四旋翼无人机进行了数值仿真实验,四旋翼无人机的模型参数如表1所示[12]。

表1 四旋翼无人机模型参数
为了对比验证本文提出的控制算法在四旋翼无人机轨迹跟踪控制中的抗外部干扰性能,分别使用串级PID控制算法、串级滑模控制(SMC)算法以及本文提出的基于扩张状态观测器的串级全局快速终端滑模控制(以下称TSMC-ESO)算法的控制结果进行对比。表2所示为TSMC-ESO控制算法的控制参数。

表2 控制器参数
仿真实验中要求四旋翼无人机做螺旋上升运动,其参考路径设置为
Pd=[0.5cos(t/2)0.5cos(t/2)2+t/10]T。
(31)
考虑到四旋翼无人机在实际飞行过程中经常受到地效干扰以及阵风扰动的影响,分别在6个状态变量x,y,z,φ,θ和ψ中加入以下时变函数来模拟外部的干扰:d1=0.5sin(πt/10),d2=0.5cos(πt/10),d3=0.5cos(πt/10),d4=0.5sin(πt/10)+0.1,d5=0.5cos(πt/10)+0.1,d6=0.5sin(πt/10)+0.2。
此外,为了对3种控制算法的控制效果进行定量比较,分别计算了四旋翼无人机在每一种控制算法下位置变量x,y,z的平方误差积分(ISE),以此来衡量四旋翼无人机轨迹跟踪控制的精度。ISE值越小,说明累计误差越小,跟踪精度越高。ISE的计算方法如下
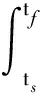
(32)
式中:ts和tf分别代表仿真开始时间和结束时间;e(t)为状态变量的跟踪误差。
图3~5所示为PID,SMC以及TSMC-ESO控制算法下的四旋翼无人机轨迹跟踪仿真结果对比图,表3所示为3种控制算法的ISE值。
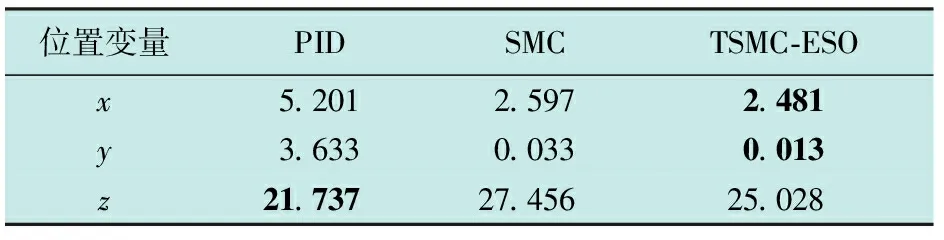
表3 3种控制算法的ISE值

图3 轨迹跟踪仿真结果
从图3和图4中可以看出,在基于扩张状态观测器的全局快速终端滑模控制算法下的四旋翼无人机跟踪轨迹最为平滑且无明显的波动现象,而在PID控制算法和滑模控制算法下的四旋翼无人机跟踪轨迹出现了较为明显的波动。
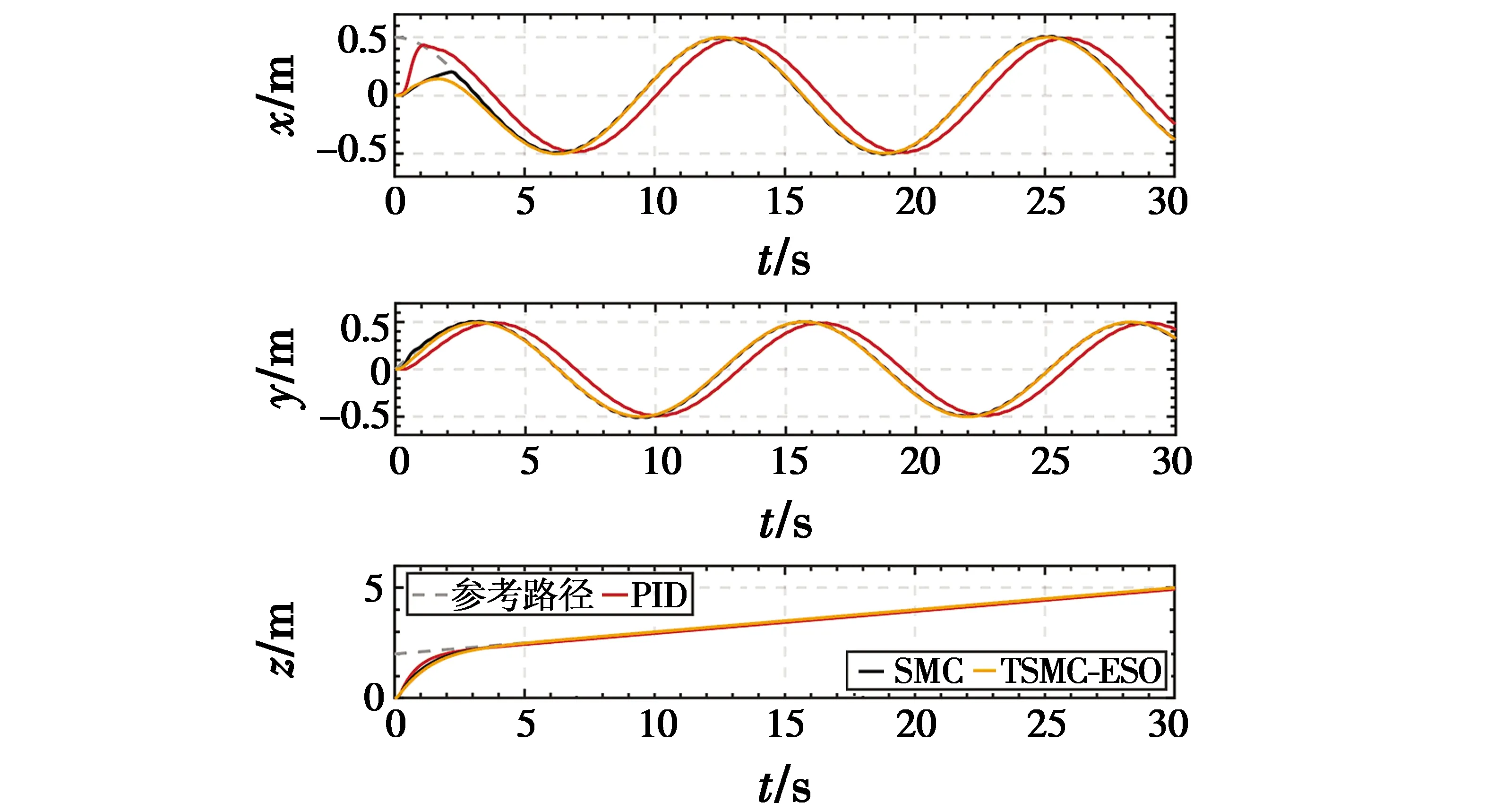
图4 位置通道跟踪对比
这一点可以从3个位置变量的ISE值得到印证。从表3中的ISE值可以看出,在水平位置变量x和y中,在TSMC-ESO控制算法下的四旋翼无人机的ISE值最低。相较于PID算法和SMC算法,在TSMC-ESO算法下的ISE值在x方向分别下降了52.30%和4.47%,在y方向分别下降了99.64%和60.61%。这说明使用TSMC-ESO算法的四旋翼无人机轨迹跟踪精度最高,跟踪误差最小,即具有更好的抗干扰性能;同时也说明了本文提出的控制算法具有良好的解耦性能,这得益于扩张状态观测器实时在线估计并补偿系统“总扰动”的功能。
四旋翼无人机滚转角、俯仰角以及偏航角的跟踪效果如图5所示。结果表明,在有时变干扰的情况下,由于传统滑模控制算法中存在切换项,串级SMC中位置控制器输出的期望滚转角信号φd和期望俯仰角信号θd出现了严重的抖振现象,这为执行器的工作带来了巨大的挑战,其在仿真开始5 s后的波动范围均为±0.16 rad。与之相比,全局快速终端滑模控制算法中无切换项,因此φd和θd的抖振现象得以消除,其5 s后的波动范围均为±0.07 rad,与串级SMC算法相比振幅下降了56.25%。串级PID下的φd,θd在5 s后的波动范围均为±0.04 rad。与串级PID相比,TSMC-ESO控制算法的性能仍然还有改进空间。此外,在串级PID、串级SMC以及串级TSMC-ESO控制算法下,四旋翼无人机偏航角ψ的波动范围分别为±0.012 rad,±0.010 rad和±0.002 rad,这说明串级TSMC-ESO算法下的四旋翼无人机偏航角跟踪精度优于另外两种算法。
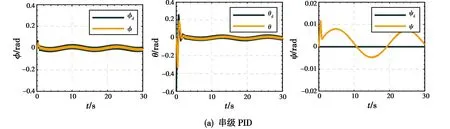
图5 姿态通道跟踪对比
5 结束语
针对四旋翼无人机的轨迹跟踪控制问题,本文设计了一种基于扩张状态观测器的全局快速终端滑模控制算法。该算法具有以下特点:1)通过引入扩张状态观测器来实现实时观测并补偿系统内外扰动的功能,较好地解决了四旋翼无人机姿态控制回路中存在的非线性、多变量、强耦合问题,提高了四旋翼无人机控制系统对内外部干扰的鲁棒性;2)通过采用带有非线性函数的终端滑模面,使得系统跟踪误差能够在有限时间内收敛,并且其控制律中不含有不连续的切换项,从而能够避免抖振现象的发生。该算法为四旋翼无人机的飞行控制算法设计提供了一种新的思路。在下一步研究中,将进一步改善所提控制算法的输出抖振现象并将其部署至四旋翼无人机平台上以验证其实际性能。

