面向弱小多目标的雷达检测跟踪算法

王科治， 胡杰民， 付连庆

(1.浙江理工大学信息学院，杭州 310000； 2.中国西南电子技术研究所，成都 610000)

0 引言

雷达可以通过无线电反射全天候探测和定位远程目标[1-3]，是现代战场上不可或缺的探测设备，同时也大量应用于民用高新技术[4]。目标跟踪是估计目标当前移动状态并预测未来移动状态的过程[5]。由于目标在复杂环境下存在密集分布、反射回波弱且掺杂大量的噪声和干扰的问题[6]，学者们开始关注多目标在复杂背景下的跟踪技术并进行了广泛研究，目前，此技术应用于民用和军用的各个领域[7],如空间监视系统、海岸检测系统、精确制导打击系统、反导系统、空中交通管理系统、气象雷达系统、无人驾驶系统等[8]。它的实现包括状态估计、数据关联、波门建立、航迹起始和终结、航迹管理、虚警和漏检等，而最为核心的是状态估计和数据关联，但是传统的数据关联算法会因回波密度的增大而出现组合爆炸情况使目标跟踪丢失。传统算法因对计算量和存储量要求高而难以实现对弱小目标的同步探测。针对非均匀杂波问题，传统算法显得不够稳健，雷达系统的误差会使其性能下降得非常严重。

针对复杂环境中各种非确定情况导致的跟踪漂移或失败的问题，文献[9]通过将更新分类器与知识训练相结合的算法有效地处理目标跟踪中出现的各种问题，但是该算法易受噪声干扰、用时长且性能不够稳定；文献[10]利用并行多传感器联合概率数据关联算法来提高跟踪精度、系统可靠性和分辨率，扩大时间和空间的可控范围，但是该算法实现设备复杂，且没有解决组合爆炸的问题。而本文利用改进的数据关联算法将目标回波与杂波区分开，能够有效地抑制噪声干扰，提高算法稳定性，并且在确认矩阵的同时，避免了互联矩阵的拆分，解决了组合爆炸问题。因为弱小目标的回波掺杂在复杂背景中易造成信号微弱且有大量噪声干扰的问题，因此，在复杂环境中检测弱小目标的技术需要不断改进。文献[11-12]利用将检测与跟踪一体化考虑的算法提高对弱小目标的检测与跟踪性能，但是该算法的实现较为复杂，对存储量与计算量要求高从而难以实现对弱小目标的同步检测。而本文通过分析目标的多普勒信息得出目标状态向量，在能量积累之前加入数据预处理过程，通过对初始的观测数据进行门限判定处理从而减小计算量。针对由斜视阵产生的逐渐变化的距离失衡杂波问题，文献[13]提出了几种基于自适应近程杂波遏制的方法，能够很好地用于幅相精确度高的情况，但当幅相误差较大时，其杂波抑制性能明显下降。文献[14]引用俯仰预滤波算法来抑制近程杂波，并使主波束杂波方向增益保持不变，但是该算法只适用于俯仰角度误差很小的情况，因此不够稳健。而本文提出了一种斜视阵条件下的非均匀杂波抑制算法，该方法充分利用了系统的空域自由度，在阵元-脉冲域进行自适应处理，在旁瓣杂波区有着良好的杂波抑制性能。

本文围绕空天目标探测识别，介绍了一种目标探测的新思路，首先，使用改进的概率数据相关算法将目标回波与杂波区分开来；同时，通过自适应方法处理阵元-脉冲域，提高了整个体系空域自由度的利用率，解决了由斜视阵产生的距离失衡问题；最后，通过多普勒信息分析计算目标径向加速度，扩大目标状态转移范围，利用统计模型对目标状态进行校正，把得到的数据进行预处理，然后再进行能量积累。仿真实验结果表明，本文所提算法能很好地对跟踪波门相互重合的目标进行跟踪，能够在跟踪误差小的情况下大幅提升关联速率，对于相邻目标的多次相对运动可以保证良好的跟踪效果，大大缩短跟踪时间的同时能够很好地控制旁瓣杂波区，从而很好地应对弱小目标，在复杂背景下可对多目标实现正确检测与跟踪。

1 问题描述

图1所示为目标相对雷达运动。

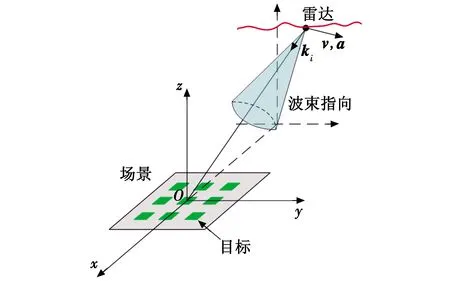
图1 目标相对雷达运动

图1中，以雷达为参考系，目标在雷达附近做相对运动。雷达工作在宽频带距离-多普勒(RD)模式下，输入数据为脉冲压缩后的时域脉冲序列。后向多普勒为负而前向多普勒为正。测试雷达采用35 GHz的载频、32 kHz的脉冲重复频率。快速时间维与采样单元之间的距离为1.875 m,距离门长度固定,包含319个采样点,门起始位置随目标移动,更新速率为1 ms,相当于32个脉冲更新一次。对于慢时间维,脉冲数是不固定的,因此需要根据读取的数据自行判定。

图2为数据经快速傅里叶变换(FFT)后的RD图实例。由图2可见，目标被隐藏于大量的杂波和干扰之中，给探测识别带来巨大挑战。

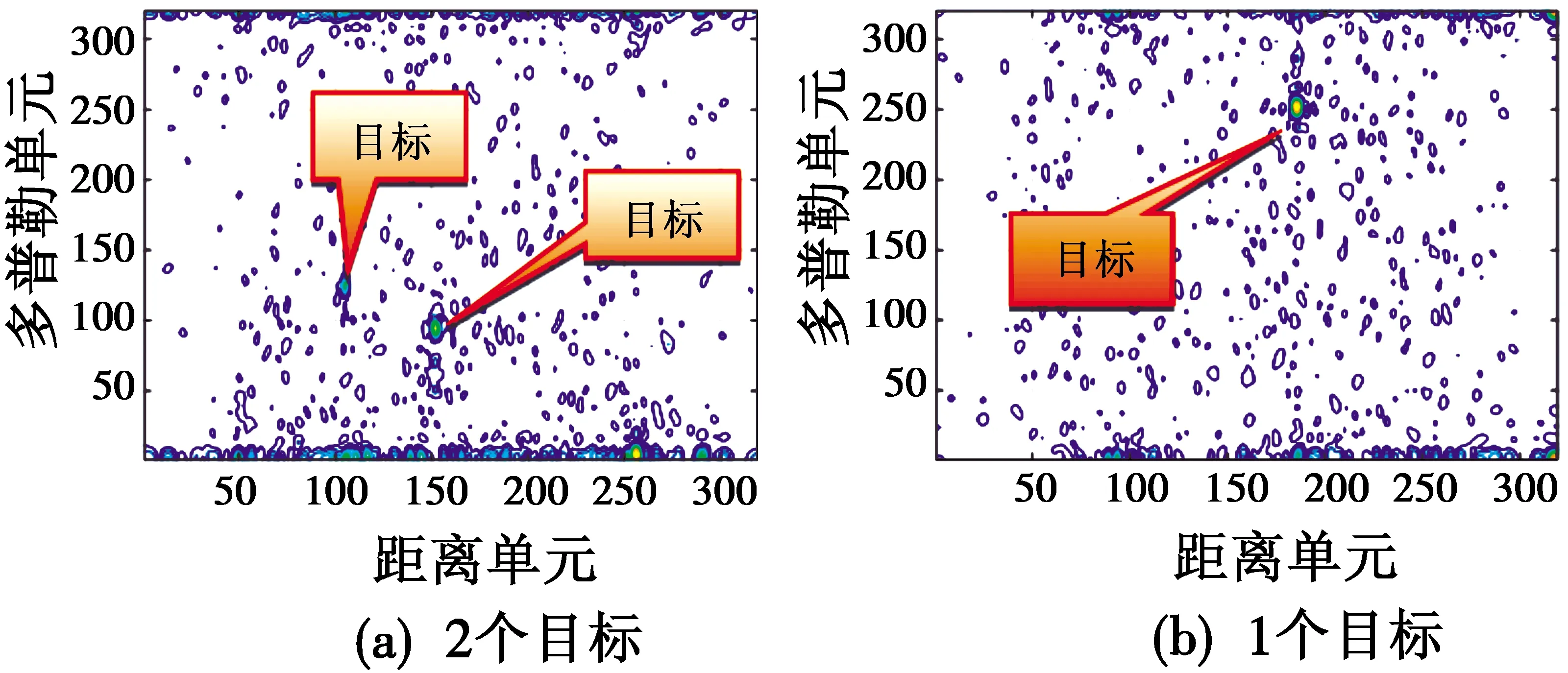
图2 数据经过FFT后的RD图实例

2 弱小目标检测与识别

2.1 多目标跟踪方案

图3所示为多目标跟踪流程。首先,将雷达回波预处理,然后进行数据关联,之后进行航迹起始或终结,对处于跟踪维持状态下的航迹进行机动判决或自适应滤波,最后输出目标状态。

图3 多目标跟踪基本流程图

雷达通常因受各种干扰的影响而无法准确地接收到观测数据，即使采用了各种信号处理办法，仍无法做到全面消除干扰。因此，为了提高雷达系统的性能，有必要事先处理观测数据。观测数据的预处理技术包括时间同步、坐标变换、空间对齐、数据压缩和异常值消除等。跟踪门的大小决定了系统的检测概率和虚警概率。数据关联能够利用雷达接收到的回波数据将目标回波与杂波进行区分，它的实现需要相关波门的帮助，相关波门能够消除大部分的干扰。航迹的起点和终点是航迹管理的决策，是目标跟踪的前提和保证。

2.2 数据预处理

对雷达接收的回波数据进行预处理的过程主要是对每个回波数据与门限值进行判定，设置门限值为VLT，通过降低VLT值来剔除噪声幅度值，从而降低能量积累过程中的噪声影响，大幅度降低计算量。

数据预处理具体算法步骤如下。

(1)

式中：ak为第k帧观测数据幅度值；Zk为第k帧量测数据集。

2)预处理：对雷达接收到的每一个数据进行门限判定，当1≤k≤K时,

(2)

3)初始化：对于初始状态s1

I1(s1)=ak

(3)

(4)

(5)

其中：Ik(sk)为阶段值函数；σ2为方差。

4)确定状态转移区域，如图4所示，其中，Ψk(sk)为k-1帧中目标的状态，Γ(sk)为状态转移区域，与目标机动性和噪声相关。

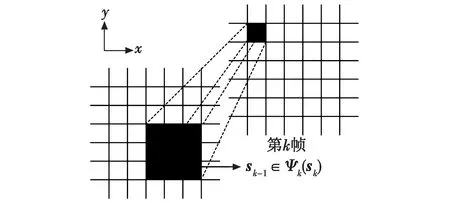
图4 帧间目标状态转移示意

对于不同的状态转移区域，都有相应的值函数与之对应，而值函数的积累过程也是目标能量积累的体现。对于2≤k≤K，所有状态sk根据CS模型确定状态转移区域

(6)

(7)

(8)

其中：(·)2表示向量的第2列元素；因子λk的取值通常难以获得，一般取0.3～0.7之间;T为脉冲重复间隔。

递归积累：对2≤k≤K，所有状态sk更新值函数及状态记录函数为

(9)

(10)

5)值函数传递。图5为值函数传递示意图，其中，ζ(sk-1)表示在第k帧中可能来自目标状态sk-1的状态集合，ο(sk-1)为集合中大概率是sk-1的状态。

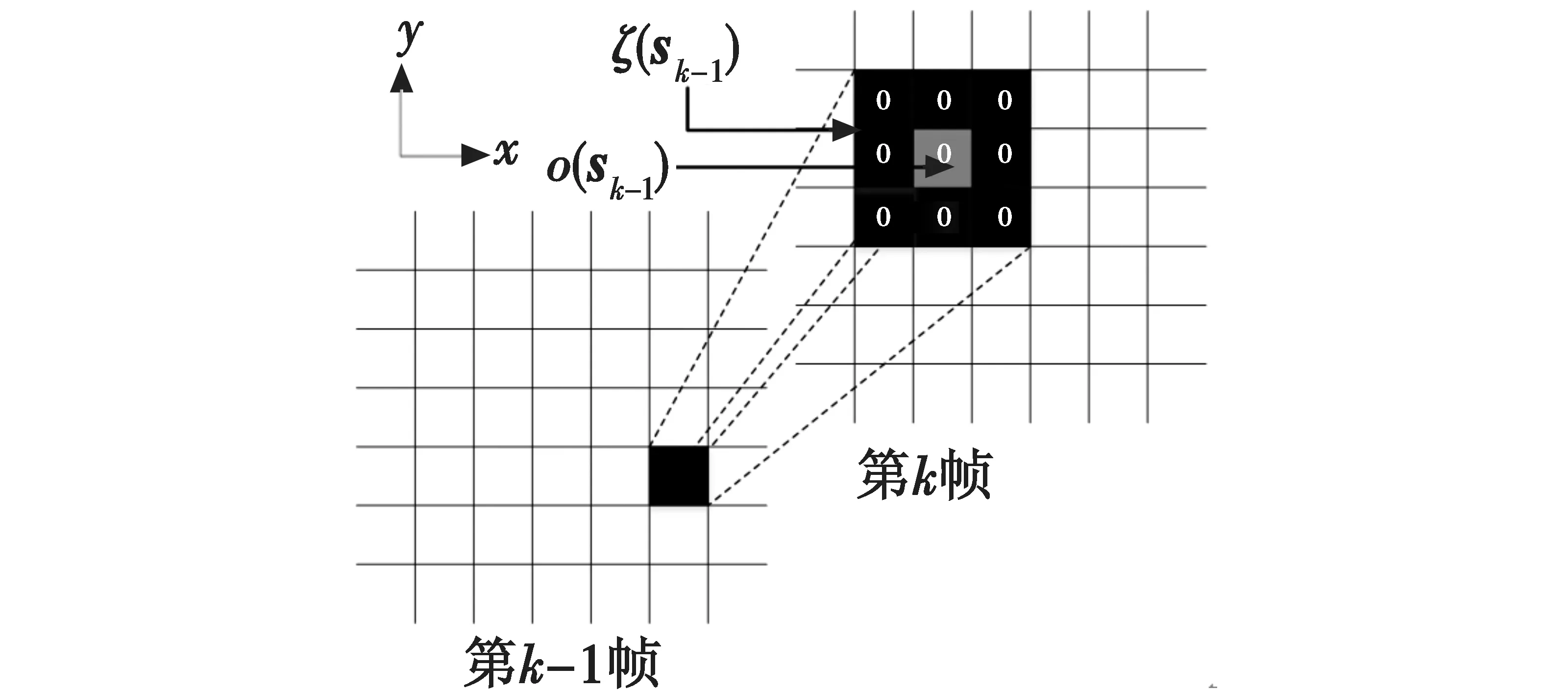
图5 值函数传递示意图

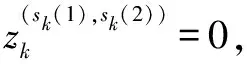
Ik(ο(sk-1))=Ik-1(sk-1)

(11)

Ψk(ο(sk-1))=sk-1

(12)

式中，ο(sk-1)表示该集合中最有可能来自目标状态sk-1的状态。

航迹回溯与目标判定的步骤与传统的基于动态规划的检测前跟踪算法(Tracking Before Detection Based on Dynamic Programming,DP-TBD)类似。在k=1时，取0作为加速度的平均值，这样就可以处理所有可能的加速度。

2.3 数据关联算法

概率数据关联算法的目标状态滤波方程为

(13)

式中，K(k)为增益矩阵，v(k)为组合新息，K(k)与v(k)直接确定滤波结果。其中,K(k)由滤波系统决定，工程上一般采用卡尔曼滤波。而对于组合新息v(k)，有

(14)

因此，滤波系统选定后，滤波结果就由互联概率βi(k)决定。在互联事件θi(k)中，除了正确回波zi(k)之外的候选回波统称为虚假观测，服从参数为λVk的泊松分布或无参数的均匀分布。本文通过引进联合概率数据关联算法(JPDA)中的聚矩阵，将虚假观测中的其他目标回波跟噪声、干扰回波区别开来，从而实现区别化处理。

具体步骤如下。

1)生成确认矩阵Ω。与联合概率数据关联算法中的定义一致，有

(15)

式中:t表示目标序号，t=0时为噪声或干扰;j为回波点迹序号;mk为k时刻确认矩阵内的回波点迹总数;wjt=1，表示第j个回波点迹位于目标t的相关波门内，wjt=0，表示回波点迹j落在目标t的波门之外。

2)定义置信系数kj=1/Nj，用来表征重合区域内第j个候选回波zj(k)属于其他目标的可能性。其中,Nj为候选回波zj(k)落入相关波门的个数，称为波门重合数。显然,当候选回波zj(k)不在波门重合区时置信系数kj为1。由于确认矩阵第1列表示候选回波来源于杂波或虚警的可能性，故元素全部为1，因此波门重合数Nj等于确认矩阵内第j行元素之和-1。

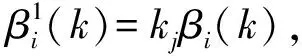
(16)

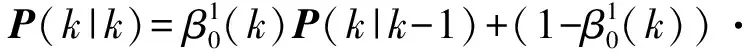
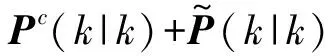
(17)

式中：Pc(k|k)=[I-K(k)H(k)]P(k|k-1),H(k)为量测矩阵；

(18)

2.4 杂波抑制

在斜视阵面的情况下，斜距不同，杂波分布也不同，所以需要提升在非均匀背景下非静止目标检测与跟踪能力，并且利用并发块的方法大幅增强计算能力。本文利用待检测单元前后的一小部分距离门作为训练数据，采用时域滑窗的形式来扩展训练样本，以保证协方差矩阵估计所需的样本数量。

本文方法处理框图见图6。

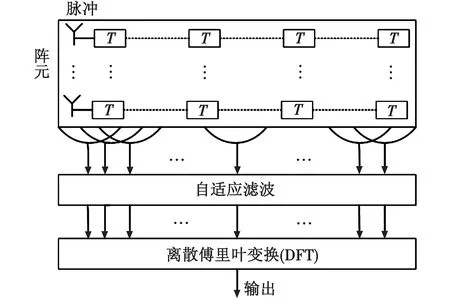
图6 本文方法处理框图

对于待检测单元(Dk,Rl)，本文算法的基本步骤为:

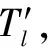
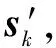
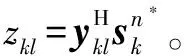
对于所有的k=1,2,…,K，l=1,2,…,L重复执行上述4个步骤。其中：Dk为第k个多普勒通道；Rl为第l个距离门。

3 实验验证

为验证本文算法的可行性，采用由某重点实验室发布的雷达回波序列中弱小飞机目标检测跟踪数据集[15]进行实验并分析结果。图7为实验仿真结果图。

测试数据集1的波门图如图7(a)所示。依据波门对距离多普勒图像进行波门对齐，图7(b)所示为数据集1在2000 ms内接收的所有脉冲利用傅里叶变换得到的总距离多普勒图，观察可得距离像已对齐。当对第n个检测点、第n×50 ms时刻目标的距离和速度进行计算时，选取该检测时刻前50 ms内1600个脉冲信号，得到对应的距离多普勒图像。可见，因环境杂波干扰太多，目标淹没在其中不易被检测到，所以先对杂波进行滤波。利用目标能量一般高于环境杂波的特性来对环境杂波进行初步滤除，根据相应时间段内能量最高点处的能量值，设定具有自适应能力的能量阈值T，将能量值超过该门限T的点认为是“疑似目标点”，将能量值低于该门限的视为环境杂波滤除，得到滤除杂波后的距离多普勒图。图7(c)中上下边缘有明显杂波，经非均匀杂波抑制后可得图7(d)。图7(d)中依然有大量杂波。经本文算法处理后可检测到位置恒定目标，如图7(e)所示，图中目标清晰可见。根据第50 ms时刻的输出数据可以得出，目标1与目标2的测量距离分别为184.28 m和382.8 m，而真实目标1与2的距离分别为180 m和380 m。目标1与目标2的实验误差分别为4.28 m和2.8 m，满足±5 m的精度要求。

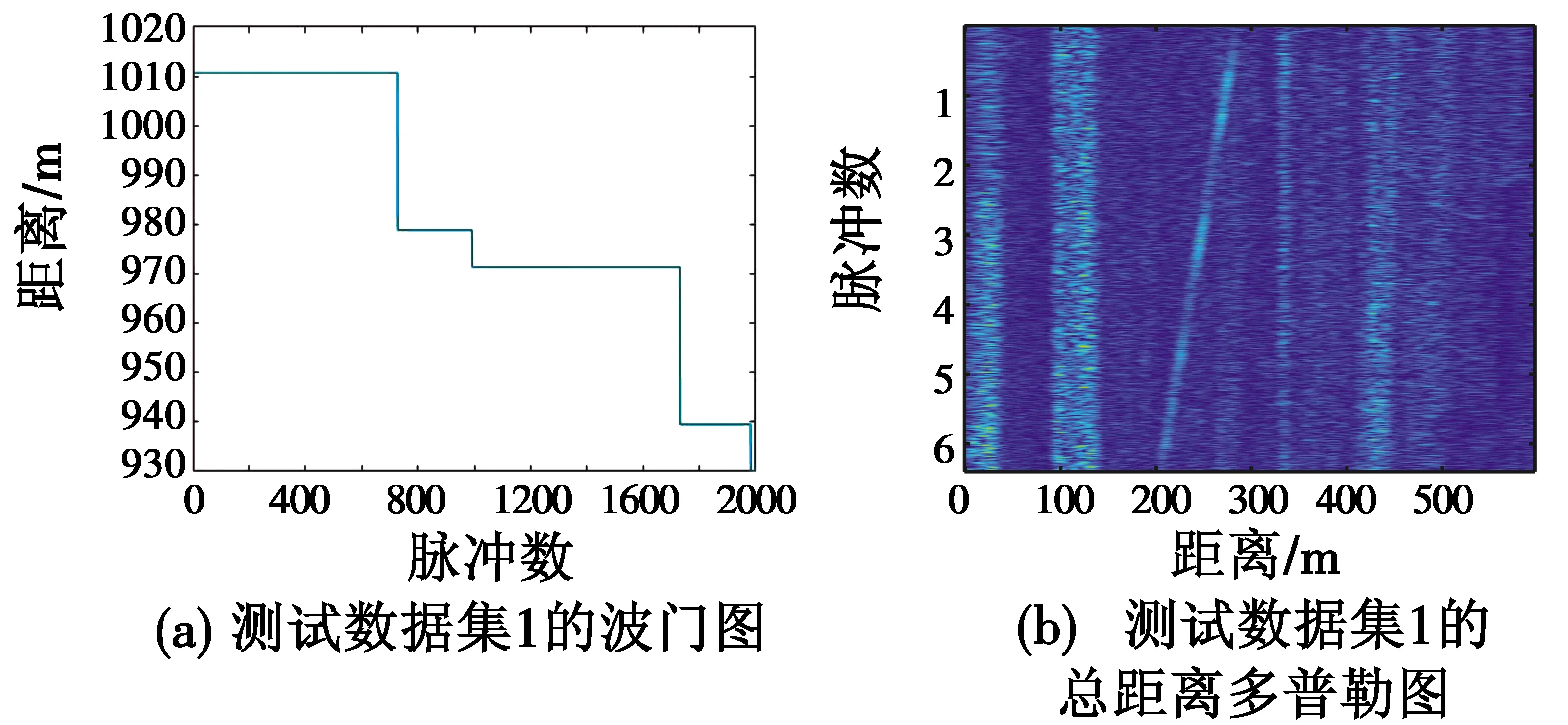
图7 实验仿真结果

4 总结展望

本文提出一个弱小多目标检测跟踪思路。首先，利用修正的概率数据关联算法实现复杂背景下目标跟踪；其次，通过自适应处理来实现斜视阵条件下非均匀杂波的抑制；最后，利用目标的多普勒信息扩展目标状态转移区域修正目标状态模型。实验雷达数据为地面背景下空中固定翼无人机目标的时域回波数据。实验结果表明，使用本文算法可以正确检测目标且估计精度满足预定要求。