互质MIMO雷达二维DOA估计新方法
章 飞, 张子菁, 杨绿溪
(1.东南大学,南京 210000; 2.江苏科技大学,江苏 镇江 212000)
0 引言
传统波达方向估计(DOA)方法一般采用均匀线阵,可估计的目标信源数都小于阵列阵元数,如MUSIC方法[1]或者ESPRIT方法[2]的阵列自由度(DOF)均受到了限制。因此,在阵元数目一定的情况下,如何优化阵列结构以获得更大阵列孔径来提高DOA估计精度和多目标的分辨能力,一直是学者们研究的热点问题[2-4]。
近年来,随着对阵元结构研究的不断深入,国内外学者提出了许多非均匀阵列结构[5-6],如互质阵列,可提高阵列自由度[5-6],并且为了提升二维DOA估计精度、抗干扰性等,多输入多输出(MIMO)雷达也被提出[7]。文献[8-9]将MIMO和互质阵列相结合对DOA进行估计,提高了其估计性能,但其采用均匀线性阵列来构造具有理想特性的有效差分阵列,这对于二维DOA估计的精度不是很高。因此,本文提出一种新的基于MIMO雷达的互质阵列组合方式(MIMO-CA),该阵列的发送阵列为特殊的不规则阵列,接收阵列则为均匀线阵,通过该新阵列组合来提高二维DOA估计精度。
文献[10]提出了将压缩感知用于稀疏矩阵的处理,降低了DOA估计的计算复杂度,但未使用MIMO互质阵列结构[10];文献[11]提出数目分别为N和N+1的并列平行排列的均匀线阵快速DOA估计方法,构造出了数目为N的子阵列,然而,该方法在信源较多的情形之下效率并不高;文献[12]提出了一种新的阵列,但在同样的阵元数目情况下无法检测到更多的信源。因此,在本文所提出阵列组合方式(MIMO-CA)的基础上,结合压缩感知的方法[13-14],提出了一种新的基于稀疏矩阵的二维DOA方法(SM-MIMO-CA)。首先,该方法构造一个稀疏阵列的等价阵列,即采用虚拟阵元的稀疏阵拓扑来解析数量更多的二维DOA信源,且能够自动匹配相应的方位角和俯仰角。其次,将二维DOA估计转化为两个独立的一维DOA估计问题,即可只估计一个变量,因此降低了计算量。然后,在信源数不少于阵元数的情况下建立起虚拟差分阵列,使用稀疏重构,并进行最小二乘运算,将稀疏矩阵通过压缩感知的方法来处理,使得M+4个阵元即可识别2M2个信源。最后,通过实验验证了SM-MIMO-CA对二维DOA估计的有效性和可靠性。
1 阵列模型与信号模型
1.1 阵列模型
MIMO的发送阵列数为4,接收阵列数为M。基于MIMO阵列模型的一些性质,能够通过虚拟化对阵列进行处理,使得虚拟后的阵列数量为4M。以此为基础的发送阵列的安置分布排列如图1(a)所示。

图1 互质MIMO阵列
如图1(b)所示,由MIMO雷达的性质得虚拟阵列,其中,互质阵列由3个稀疏线性均匀的阵列组成。选择的M∈N+和2M∈N+为互质。令2M=N,本文设阵列传感器位于
{(x,y)|(0,M2md)∪(d,Nm1d)∪(d+Ld,MNd+Nm2d)}
(1)
式中:2m∈[0,2M-1],m1∈[1,M-1],m2∈[0,M-1],m,m1,m2∈N+;(x,y)表示X-Y平面中的坐标。
1.2 信号模型
本文中,子阵列的排放方式不再是共线的,而是分别按照距离为d和距离为Ld(L∈N+)的长度间隔平行排列放置。并且,随着L的不断增大,阵列的孔径同样会不断增大,其分辨率也达到更高的精度。然而,孔径过大,会让信号变得相关,因此,L的取值大小应该合理斟酌,不能太大。假设虚拟后的关系为
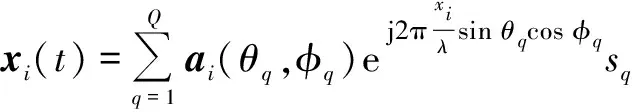
(2)

(3)
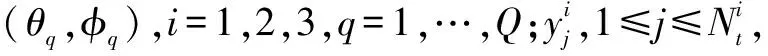
本文方法需要将二维DOA估计问题变成两个独立的一维DOA估计问题,cosαq=sinθqsinφq,cosβq=sinθqcosφq,αq,βq∈[0°,180°],分别表示入射方向与Y轴、X轴的夹角,进而
(4)
(5)
假设s(t)=[s1(t)…sQ(t)]T,表示信号向量,而Ai=[ai(α1)…ai(αQ)],表示子数组i所对应的阵列流形,那么被接收到的数据向量就表示为
xi(t)=AiBis(t)+ni(t)
(6)
(7)
在传统方法中,虽然能够实现分辨率较高的DOA估计,但是要获得合适的噪声子空间需要满足条件Q (8) (9) M与N互质,此属性使得虚拟阵列中所包含的冗余元素数目较少,因此,其共阵列中的自由度将会大幅度增加,可以满足在阵元较少的情形下对更多的信源进行估计的要求。 基于上文所提的MIMO-CA阵列模型以及信号模型,zik,1≤i,k≤3,信号向量能够在全部离散的角度网格上被稀疏表示为 (10) zik=Φ°ikb°ik+εik1≤i,k≤3 (11) zik所属的导向矩阵为 (12) (13) (14) (15) (16) (17) (18) F=diag(γ1,…,γG,γ1,…,γGα)。 (19) (20) (21) (22) (23) (24) (25) (26) 为了验证本文方法的有效性,将本文方法与文献[12]的TPAUL方法、文献[15]的TDUL-PM方法、文献[18]的TDSR-CS方法、文献[19]的PUL-RARE方法进行对比。 当可估计最大信源数量Qav=MN=M2时,且在一维的情形下得到的共阵与传统互质阵列是等价的。对于给定物理天线数量Nt=2M+N-1=4M-1,Qav=MN=M2,且Nt=2M+N-1=4M-1,M 阵列数与可估计信源数的关系如图2所示。 图2 阵列数与可估计信源数的关系 从图2中可以看出,所有方法的Qmax值虽然都随着Nt的增加而增加,但基于互质阵列的方法相较于其他方法明显更优。 3.2.1 信噪比与均方根误差的关系 进行100次蒙特卡罗仿真,设M=4,L=20,即Nt=4M-1=15。假设Q个远场源具有相同功率,并且在仰角平面(θq,φq)上,θq∈[0°,90°],φq∈[-90°,90°],q=1,…,Q。角度空间中的网格间隔为0.1°,除此之外,设置贝叶斯稀疏学习组所涉及的参数a=b=c=d=0。 图3给出了当信源数为3、快拍数为500时,不同信噪比(SNR)下,对比的各种方法的RMSE变化情况。本文SM-MIMO-CA方法和PUL-RARE方法在俯仰角方面性能比较接近;在方位角方面,当信噪比为0时,SM-MIMO-CA方法相比于其他方法都有不小的提升。通过比较不同信噪比下的RMSE得出,在低信噪比下SM-MIMO-CA比其他几种方法的估计性能都更好。 图3 信源数为3时均方根误差与信噪比之间的关系 3.2.2 角度与快拍数之间的关系 信源数为3时均方根误差与快拍数之间的关系如图4所示。 图4 信源数为3时均方根误差与快拍数之间的关系 从图4中可以看出,在信源数为3且信噪比为0的情况下,本文方法整体性能相对其他方法有不小的改善。实验结果表明,本文方法在不同快拍数情况下的性能均优于TPAUL方法以及PUL-RARE方法。 3.2.3 二维DOA估计对比 通过上述实验验证了本文方法在低信源、不同信噪比、不同快拍数情况下的DOA估计性能,之后完成了多信源实验。设信源数目为Q,其数目大于阵列的数目,并将信噪比保持成0,将快拍数设置成500,将其与TDSR-CS方法进行对比分析,得到实验结果如图5所示。 图5 二维DOA估计对比 由图5中两种方法的DOA估计性能结果可以看出,本文方法相较于TDSR-CS方法更接近真实的角度值,这表明本文方法具有更优秀的二维DOA估计性能。 本文首先提出了一种新的MIMO互质阵列模型,该模型可以有效地估计阵列数目较少的多个信源,并提高DOF和DOA估计的准确性。在此基础上进一步提出了一种新的基于互质阵列的MIMO雷达二维DOA估计方法(SM-MIMO-CA),并结合压缩传感理论来处理已经稀疏处理的MIMO互质阵列。通过实验可得,该方法能够在信源较多的情况下具有较高的分辨率,同时还具备较高的角度估计精度,可以增强DOA估计的DOF。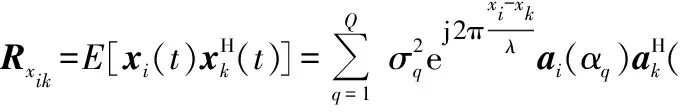

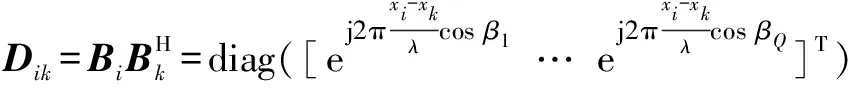
2 基于MIMO-CA的二维DOA估计方法


3 实验结果与分析
3.1 自由度分析
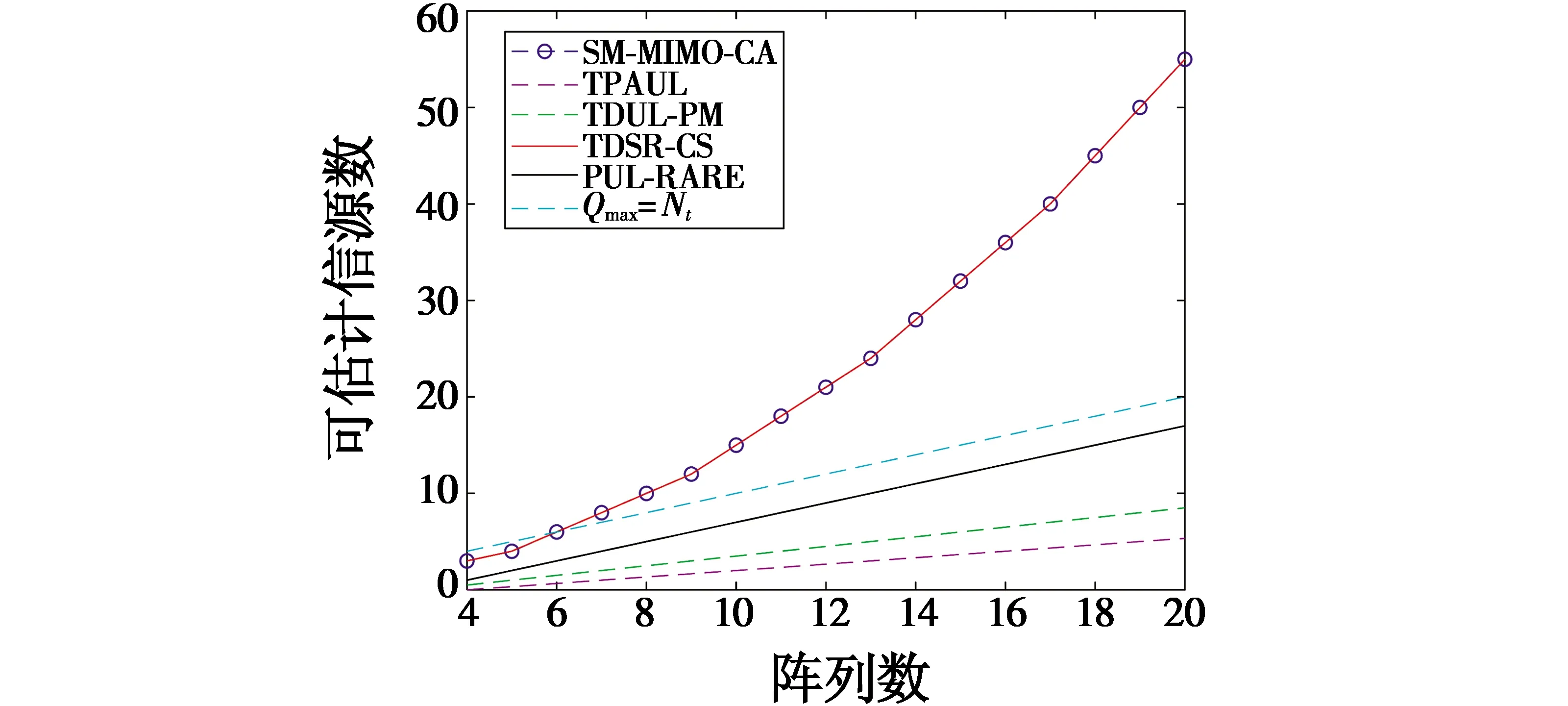
3.2 二维DOA估计性能比较
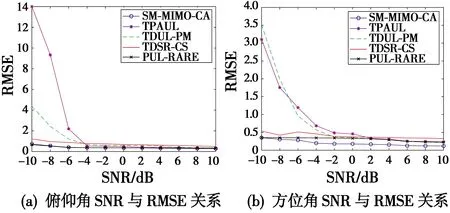
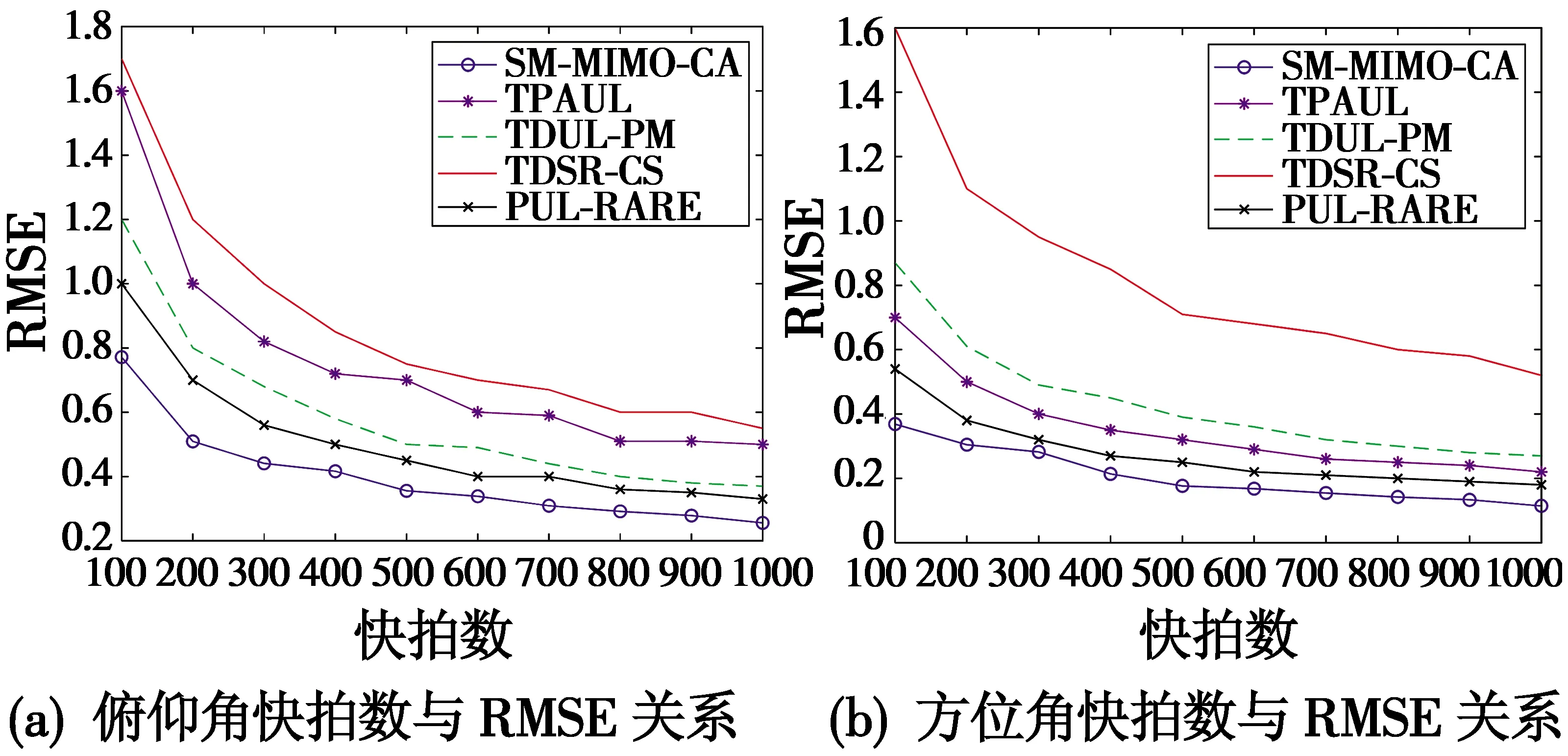

4 结束语

