发生函数在组合恒等式证明中的应用

◎罗志敏 (江门职业技术学院教育与教育技术系，广东 江门 529090)

1 引言

组合恒等式是组合数学研究的重要内容，它在概率论、计算机算法、工程计算等诸多领域有着广泛的应用，因此它引起了许多数学工作者的兴趣.发生函数又称为母函数或生成函数，是解决离散数学问题的有效工具.我们运用发生函数也可巧妙地将离散和连续问题有机结合.将发生函数应用于组合恒等式的研究，可以突破组合恒等式的一些机械化证明，大大减少计算量.本文首先给出了发生函数的基本定义，然后简述利用发生函数解决问题的基本思路，最后运用发生函数证明了一些组合恒等式.

2 基本定义、方法概述与引理

首先介绍形式幂级数.所谓形式幂级数，是指形如a0+a1x+a2x2+…的表达式.其中{an}n∈N为形式幂级数的系数序列.

引理1(组合变换互逆公式)：设g(x)为任一函数，f(n)定义如下：

则有

这里f(0)=g(0)，且也可由g(n)推出f(n).

3 发生函数法的应用

以下给出几个关于组合恒等式的命题，展示发生函数的具体应用.

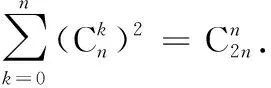
证明取发生函数f(x)=(1+x)n，x∈(-1,1)，同时，

f(x)=(1+x)n

(1)

f(x)=(1+x)n

(2)

将(1)式用2n替换n，有：

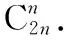
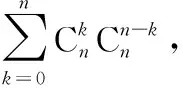
证明取发生函数f(x)=(1-x)2n，g(x)=(1+x)2n，x∈(-1,1)，同时，

(3)

(4)

将(3)(4)式对应相乘有：

对于(3)式，用x2替换x可得：

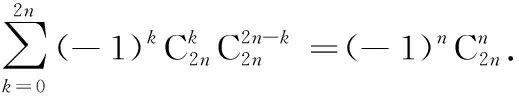
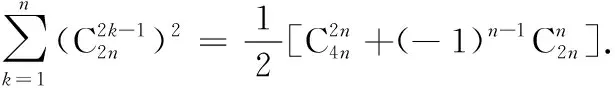
将以上两等式两边对应相加可得：

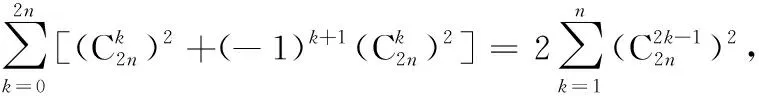
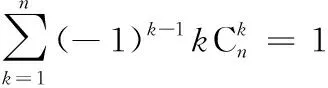
(ⅱ)当n≠1时，取发生函数f(x)=-(1-x)n，将f(x)展开可得：

则原命题成立.

证明(1)对于任意的n∈N,当m=0和m=1时，等式成立是明显的.

(2)当m≠0,1时，以下用数学归纳法证明等式也是成立的：

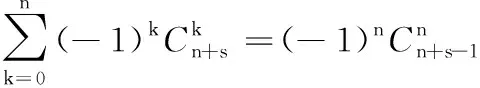
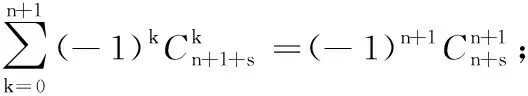
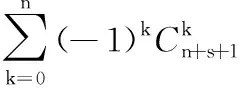
所以当m=s+1时，等式成立.由数学归纳法可知原命题成立.

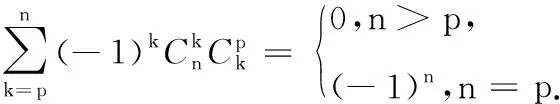
证明取发生函数f(x)=(1+x)n，对f(x)求p(n≥p)阶导数有：

f(p)(x)=n(n-1)·…·(n-p+1)(1+x)n-p

(ⅰ)当n>p时，取x=-1，则有

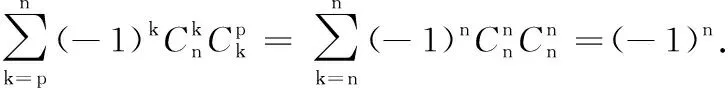
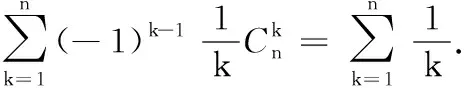
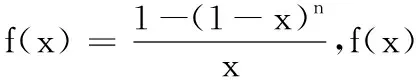
将f(x)在[0,1]积分有：

将f(x)做如下表示：

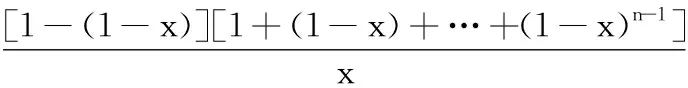
同样对此f(x)在[0,1]积分有：

综合以上可知原命题成立.

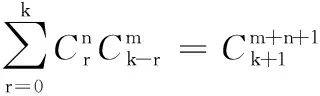
证明当|x|<1时，有如下幂级数展开式：

取发生函数：

=(1-x)-n-1·(1-x)-m-1=(1-x)-n-m-2

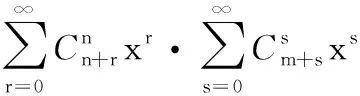
最后令n+r=q，m+p-r=k-q，则有n+m+1+s=k+1，于是可以得到：

将上式中的q改写成r，即可得原命题成立.

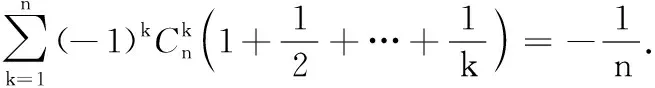
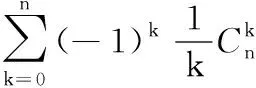
=f(n).

再由引理1中f(n)与g(n)的互逆性，可以得到：

注：以上几个命题如果仅用组合数的运算性质来证明，将会非常烦琐，由此可见发生函数法在解决组合数问题中的优越性.