一道错题的求证与警示
◎王永军 (重庆市广益中学校,重庆 南岸 400065)
一、预备知识
下面给出本文用到的一些公式、结论.
(一)三角函数诱导公式与变换公式
2.sin(-α)=-sinα.
3.sin(α+β)=sinαcosβ+cosαsinβ,
cos(α+β)=cosαcosβ-sinαsinβ.
4.sin 2α=2sinαcosα,
cos 2α=cos2α-sin2α=2cos2α-1=1-2sin2α.
(二)比例性质与均值不等式
1.合分比性质:

2.均值不等式:
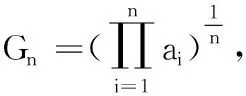
Gn≤An,等号成立,当且仅当所有ai都相等.
(三)三角形中的一些结论
在△ABC中,内角A,B,C的对边分别为a,b,c.
1.A+B+C=π,sinA=sin(B+C).
其他两种形式:sinB=sin(C+A)、sinC=sin(A+B).
3.余弦定理:c2=a2+b2-2abcosC.

其他4种形式:a2=b2+c2-2cbcosA,b2=a2+c2-2accosB.
事实上,
sinA+sinB+sinC
=sinA+sinB+sin(A+B)
=sinA+sinB+(sinAcosB+cosAsinB)
=sinA(1+cosB)+sinB(1+cosA)
6.sin 2A+sin 2B+sin 2C=4sinAsinBsinC.
事实上,
sin 2A+sin 2B+sin 2C
=sin 2A+sin 2B+sin 2[π-(A+B)]
=sin 2A+sin 2B-sin(2A+2B)
=sin 2A(1-cos 2B)+sin 2B(1-cos 2A)
=2sinAcosA·2sin2B+2sinBcosB·2sin2A
=4sinAsinB(cosAsinB+cosBsinA)
=4sinAsinBsin(A+B)
=4sinAsinBsinC.
7.三角形中两边之和大于第三边;三角形中两边之差小于第三边;三角形中大边对大角;三角形中大角对大边.
二、原题重现
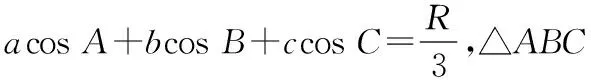
A.a+b+c=4
B.R=6
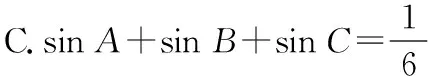
三、经典解答
这是一道多项选择题,涉及的知识点很多、很深,解题难度很大.现在结合题干(题目条件)、选项(判断正误)进行发散思维、展开联想,力求突破求解.
(一)选项分析
对于选项A,由△ABC的内切圆半径(r)、面积(S△ABC)与周长(a+b+c)建立联想.
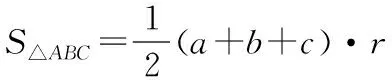
acosA+bcosB+ccosC
=2RsinAcosA+2RsinBcosB+2RsinCcosC
=Rsin 2A+Rsin 2B+Rsin 2C
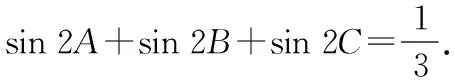
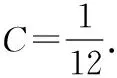
解得R=6.选项B正确.
对于选项C,由正弦定理、选项A、选项B、合分比性质进行验证.
事实上,
即有,
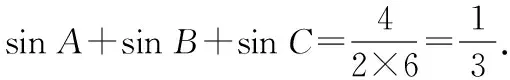
综上分析,本题应该选择选项ABD.其实这是一道错题!因为这样的△ABC根本就不存在!
(二)错在哪里
考虑△ABC的三边a,b,c,从(一)的求证过程中已经得到,
a+b+c=4,abc=144.
由均值不等式,
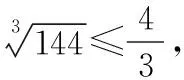
四、改进意见
在命制数学问题的时候,常常借用特定的模型(如正三角形)作为背景材料,因为这样可以有效地回避“错题”.
上述问题可以改进如下:
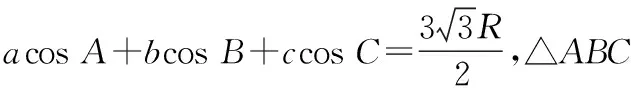
R=6,
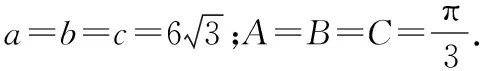
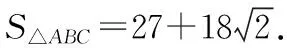
sin 2A+sin 2B+sin 2C=2.
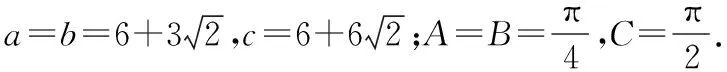
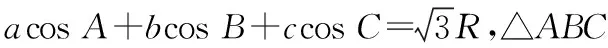
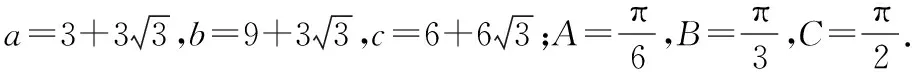
五、教学警示
(一)精彩的练习题
作为平时教学中的练习题,教师可以让学生在各个知识点的交汇处进行综合练习,努力提升学生的数学学科素养,让数学核心素养落地有根.
三角函数的变换形式各异、精彩纷呈,是处理三角函数问题的基本工具之一.变换中要注意定义域、值域的适用条件、适用范围的变化,防止出现“错题”.教师在教学中要有意培养学生的思辨意识,要敢于挑战权威、大胆质疑,努力培养学生的创新性思维品质.下面再看一个补充例题:

解析:本题的“标准答案”为ACD.原因如下:
先求出C.
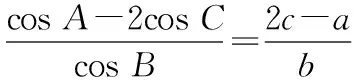
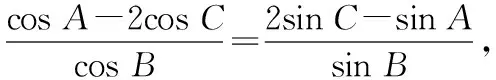
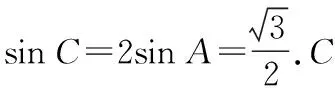
下面来分析题目中其他的条件,再来分析角A,B.
注意到sinC>sinA,故c>a,从而C>A,这表明A为锐角,于是
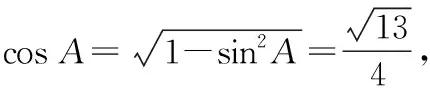

这表明△ABC中的三个内角已完全确定,下面考虑△ABC的三边之长.

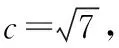
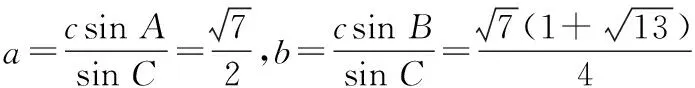
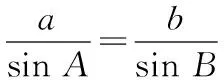
对吗?
这里求解的全过程都是完美的、是绝对正确的!那错在哪里呢?错在△ABC根本就不存在!

(二)精致的测试题
数学的测试题、考试题是准确的、精致的,科学性是命制数学问题的首要前提.试题的正确性是命制数学问题的根本要求.试想一道“错题”,不管多么“综合”、多么“高深”、多么“华美”,实际上都是舍本求末、无稽之谈.数学测试中“错题”对学生的伤害是巨大的、显而易见的:影响测试时的心情、丧失后继学习的兴趣.
教师在命制与三角形相关的试题时,最好先设置好“框框”(模型),再去“填空”,减少命制试题的盲目性,做到有据可依、有本有源.

