含忽略工序和不相关机的混合流水车间调度
轩华,樊银格,李冰
(郑州大学 管理工程学院,河南 郑州 450001)
含忽略工序的混合流水车间调度(hybrid flowshop scheduling with missing operation,HFSMO)在炼钢、不锈钢、塑料等制造工业较为常见。在经典混合流水车间调度问题中,通常假定工件经所有工序处理,但在实际生产中,工件会忽略某些工序,即一些工件可能不经某些工序处理,如炼钢-连铸生产中,由电弧炉或转炉生产的钢水要在高温下经精炼和连铸工序进行加工,不同的钢种对生产路线的要求会有所不同,像Q235普通碳钢要略过RH(Ruhrstahl-Hausen)真空精炼炉阶段[1]。考虑到并行机的新旧程度或异构性,由此衍生出本文所研究的带不相关并行机的HFSMO。由于HFS (hybrid flowshop scheduling)问题是NP-hard[2],带不相关并行机的HFSMO 是HFS 问题的扩展且其更为复杂,它不仅要确定工件的处理序列,还需确定工件在每道未忽略工序的机器分配,所以本文研究的更复杂的带不相关并行机的HFSMO 也是NP-hard。
目前,已有不少学者研究HFSMO。就两道工序的HFSMO 而言,Tseng 等[3]研究了工序1 有一台机器且工序2 有两台同构机的情况,假定工序1 可忽略,提出了一种启发式算法以最小化最大完工时间。就含同构并行机的多工序HFSMO 而言,为最小化最大完工时间,Saravanan 等[4-5]提出了遗传算法、模拟退火算法和粒子群算法,Marichelvam等[6]基于遗传算法和分散搜索算法提出了一种改进的混合遗传分散搜索算法,Dios 等[7-8]提出了一些分派规则和改进启发式来求解该问题;为最小化平均拖期,Saravanan 等[9]提出了遗传算法与模拟退火算法;为最小化平均滞留时间、总提前、总拖期和关键机器跳过率的加权和,Li 等[10]针对铁水系统提出了一种改进离散人工蜂群算法;为了最小化最大完工时间、总等待时间以及处理时间与标准处理时间的偏差之和,Long 等[1]针对炼钢-连铸生产系统提出了一种改进遗传算法。
目前,已有不少学者在不相关并行机环境下研究HFS 问题。针对单目标问题,Meng 等[11]研究了节能HFS,并提出改进的遗传算法以最小化机器闲置消耗。为最小化最大完工时间,Qin 等[12]研究了批量调度HFS,提出两阶段蚁群算法;罗函明等[13]针对多工序HFS,提出离散布谷鸟算法;轩华等[14]针对带有限缓冲HFS,提出基于遗传算法和禁忌搜索的混合启发式算法。针对多目标问题,Zhou 等[15]研究了带模糊处理时间的HFS,设计差分进化算法以最小化总加权交付损失和总能耗。Yu 等[16]针对带机器能力约束和依赖加工序列设置时间的HFS,提出带多重解码框架的进化算法以最小化总拖期和总设置时间。Zhou 等[17]研究了带节能区间的HFS,提出新的帝国竞争算法以解决以总能耗和最大完工时间为目标的双目标问题。
就目前查阅的文献而言,HFSMO 已引起众多学者的关注,既有的研究聚焦于同构机环境。现有的带不相关并行机的HFS 不考虑带忽略工序特性,关于不相关并行机环境下HFSMO 问题的研究尚缺乏,还有待进一步探讨。就优化算法而言,文献[1,3-10] 的研究说明了进化算法求解HFSMO 问题有较大潜力,如文献[4,9]利用单独的遗传算法和模拟退火算法求解含同构机的最大完工时间问题。混合算法通常能扩大搜索的范围,提高解的质量,因此关于混合算法求解这类问题的研究还有待进一步探讨。候鸟优化(migrating birds optimization,MBO)算法作为一种新兴的群智能优化算法,已广泛应用于生产调度领域,如流水车间调度[18-21]、混合流水车间调度[22-23]和柔性作业车间调度[24-26],它最早是由Duman 等[27]提出并应用于二次分配问题。因此,本文结合全局搜索、自适应遗传算法和候鸟优化提出一种遗传候鸟优化算法(genetic migrating birds optimization algorithm,GMBOA)解决含不相关并行机的HFSMO,通过仿真实验验证所提算法的有效性和可行性。
1 问题描述与建模
1.1 问题描述
含不相关并行机的HFSMO 问题包括来自集合J={1,2,···,n}且将在h道工序上处理的n个工件,每道工序s有ms台不相关并行机,即对于每道工序,工件在ms台并行机上的处理时间相互独立,仅取决于工件与机器的匹配程度。每个工件可能会忽略某些工序。每台机器一次只能处理一个工件,而每个工件一次至多在一台机器进行处理。调度目标是确定工件处理序列和机器分配,以最小化最大完工时间。所研究问题的其他假设如下:
1)工件的开工应在其释放时间之后;
2)机器准备时间与工件顺序无关,且包含在处理时间中;
3)所有机器在整个计划时间段内连续可用;
4)工件一旦在某台机器上开始处理后,不允许中断,直至该工序完成;
5)工件处理无优先级要求;
6)工序之间的转移时间忽略不计;
7)相邻工序之间的缓冲区容量无限。
1.2 模型构建
由前述可知,每个工件j实际访问的总工序数Oj≤h,虽然工件需经h道工序完成其处理任务,但部分工件j的处理略过了h−Oj道工序,即这些工件未经h−Oj道工序处理而直接进入后续工序。含不相关并行机的HFSMO 模型如下:
所研究问题的目标是满足所有约束条件下最小化最大完工时间Cmax,即

式中:Cjh表示工件j(j=1,2,···,n)在工序h的完工时间。式(2)通过检查工件在最终工序h的完工时间,确定最大完工时间。

式中:ms为工序s(s=1,2,···,h)可利用的机器数;F为一个足够大的数;Pjks为工件j在工序s的机器k(k=1,2,···,ms)上的处理时间;Wjs为二元参数,若工件j在工序s上处理,其值为1,否则为0;Bjs表示工件j在工序s的开工时间;Xjks为二元变量,若工件j在工序s的机器k上处理,其值为1,否则为0。式(3)定义了工件在每道工序的完工时间,若工件j未在工序s处理,则它在该工序的完工时间为它在紧前未忽略工序的完工时间。
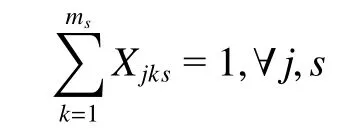
该约束确保每个工件在任一工序只能分派到一台机器进行处理。
Cjs≤Bj,s+1,s∈{1,2,···,h−1},∀j
该约束说明了每个工件只完完成前一工序的处理任务后方可开始下一道工序的处理。
Bj1≥Rj,∀j
式中Rj为工件j的释放时间。该约束描述了工件只有到达生产系统才可开始处理。
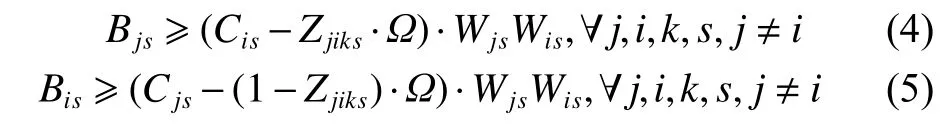
式中:Zjiks为二元变量,若工件i和j在工序s的机器k上处理且工件j早于工件i,其值为1,否则为0。这两个约束表示:同一道工序分派在同一台机器处理的两个工件之间的优先级关系,若Zjiks=0且Wjs=Wis=1,约束式(4)描述了工件j在工序s的机器k上的开工时间必须在工件i的完工时间之后,若Zjiks=1且Wjs=Wis=1,约束式(5)描述了工件i在工序s的机器k上的开工时间必须在工件j的完工时间之后。

约束式(6)、(7)定义了变量取值范围。
2 遗传候鸟优化算法
遗传算法已广泛用于求解HFSMO 问题,为使遗传算法有效求解含不相关并行机的HFSMO 问题,设计基于机器号的编码方案,采用考虑机器处理时间的全局搜索和随机程序生成初始种群以提高初始解的质量,设计自适应更新策略以计算交叉概率 ξ及变异概率 ψ,以此执行交叉和变异操作。最后,引入结合邻域搜索的候鸟优化算法以扩大遗传算法解的邻域搜索范围,从而获得较好的近优解。
2.1 编码、解码和适应度选择
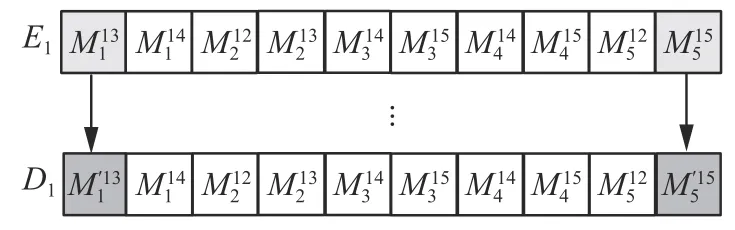
含不相关并行机的HFSMO 需确定工件在每道工序的机器分配,因此设计基于机器号的整数编码方案以表述机器分配序列 σ。考虑到HFS 的多工序处理需求,令每个工件所忽略的工序数不超过h−2,根据忽略工序比例p,随机产生每个工件的未忽略工序信息序列 τ,如图1(n=5,h=5和p=0.6),其中表示工件j在阶段s的工序;然后基于 τ生成相应工件的机器号,为平衡并行机器的负荷,令其值满足[1,ms]的均匀分布,从而形成长度为n·h·(1−p)的一个染色体,其中每个元素(即工序位上的数值)为对应工件所在工序分配的机器号。

图1 未忽略工序信息序列Fig.1 Information sequence of unmissing operations
初始化种群时,由于每道工序所含的机器为不相关并行机,考虑不同的机器处理同一工件的时间不同,而最大完工时间与工件的处理时间相关。因此,基于张国辉等[28]的研究提出考虑处理时间的全局搜索以产生一个个体,而其他个体则由随机程序生成。令数组θ={ps11,ps21,···,,ps12,···,,ps1h,ps2h,···,}为记录从工序1 到工序h的每台机器的累计处理时间的一维数组,其初始值均设为0,全局搜索从任一工件j开始,对它的第一道未忽略工序u,将可利用并行机的工件处理时间分别与数组 θ内该机器位置的数值相加,即对k=1,2,···,mu,计算{Pjku+psku},从中选择累计处理时间最短的机器k′作为工件j在工序u所分配的机器,将该机器号填入个体内工序位(h(1−p)(j−1)+1),令psuk′=min{Pjku+psku},更新数组θ;然后,对工件j的第2,3,···,h(1−p)道工序重复上述过程,从而完成该工件所有工序的机器分配。接着,再从剩余工件集内随机选择一个工件执行上述过程,直至完成所有工件未忽略工序的机器分配。结合随机程序产生的(e−1)个个体共同构成了如图2 所示的种群规模为e的初始种群。

图2 初始种群Fig.2 Initial population
为计算最大完工时间,需为分配至同一台机器的工件进行排序,为此,设计了基于最短处理时间的解码方案,即对于机器分配序列 σ,当s=1时,将分派到在同一台机器处理的工件按照最短处理时间规则进行排序,当s>1时,对同一台机器上处理的工件采用先到先加工规则生成处理序列,然后基于最早空闲机器原则依次将各工件安排在所分配机器。对于工件的忽略工序,则按照约束式(3)确定其在忽略工序的完工时间。
本文的目标是最小化最大完工时间,故将适应度函数表示为目标函数的倒数,即个体g的适应度函数为F(g)=1/Cmax(g)。采用轮盘赌选择法,个体适应度值越大,被选择的概率也越大。
2.2 交叉操作
采用单点交叉和均匀两点交叉两种方式执行交叉操作。在0 和1 中随机生成一个整数v,当v=0时,执行单点交叉,即随机选择两个父代个体E1和E2,随机生成一个工序位x(1≤x≤n·h·(1−p)),交换E1和E2中所选工序位x的机器号,保持其他工序位的机器号不变,从而生成子代个体D1和D2,如图3。当v=1时,执行均匀两点交叉,首先,随机选择两个父代个体E1和E2,随机生成两个工序位x和y(1≤x 图3 单点交叉Fig.3 Single-point crossover 图4 均匀两点交叉(q=1)Fig.4 Uniform two-point crossover(q=1) 采用自适应更新策略确定交叉概率ξ,用以确定是否执行上述交叉操作,计算如下[29]: 式中:λ为当前迭代数;β为最大迭代数;Favg为当前种群的平均适应度值。 变异操作是根据变异概率通过改变父代个体的机器号以产生子代个体的过程。本文提出了基于随机机器选择的单点变异和基于机器最短处理时间的多点变异两种方式。 1)基于随机机器选择的单点变异 从父代个体E1中随机选择一个工序位x(1≤x≤n·h·(1−p)),将该工序位的机器号重新在[1,ms]之间随机生成,如图5。 图5 基于随机机器选择的单点变异Fig.5 Single point mutation based on random machine selection 2)基于机器最短处理时间的多点变异 推广Chang 等[29]的研究,提出基于机器最短处理时间的多点变异操作。从父代个体E1依次取出工序位x的机器号,比较从区间[0,1]生成的随机数w与变异概率 ψ,若w<ψ,则从工序位x可利用的并行机中选择处理时间最短的机器替换原有机器号,否则,保持原有机器号不变,对个体内所有工序位完成上述操作后,生成新个体D1,如图6。 图6 基于机器最短处理时间的多点变异Fig.6 Multi-point mutation based on the shortest processing time of the machine 自适应变异概率ψ由式(8)确定: 为提高算法的搜索能力,进一步改善遗传算法解的质量,设计引入基于工件、机器和工序位的3 种邻域搜索结构的候鸟优化算法。 1)邻域搜索结构N1 随机选择一个工序u,从在该工序处理的工件集中随机生成两个工件 π1和 π2,将它们在该工序处理的机器号进行交换,重复该过程直至达到最大循环次数Lmax。 2)邻域搜索结构N2 从机器集中寻找处理工件数超过两个的机器,分别计算每台机器上工件处理时间之和,从中获取具有最大总处理时间的机器k′,进而得到它对应的工序u,从该机器处理的工件集中选取处理时间最长的工件 π,将 min{Pπku}(k=1,2,···,mu)对应的机器作为该工件分配的机器。 3)邻域搜索结构N3 随机生成一个工序位x,确定它所对应的工件π=和工序u=x−π·h·(1−p),将该工序位的机器号依次设置为1,2,···,mu,分别计算相应个体的适应度值,从中选取适应度值最大的机器号填入该工序位,重复该过程直至达到最大循环次数 ηmax。 引入上述邻域搜索结构执行候鸟优化算法,具体步骤如下: 1)参数初始化。设置Lmax、ηmax以及候鸟优化最大迭代数 γ,巡回数Gmax,令=1,G1=1,α=1,候鸟种群规模为 δ。 2)初始种群生成。设计初始种群由3 部分构成:①对每个工件的未忽略工序,从可利用的并行机中选择工件处理时间最短的机器作为该工件分配的机器,从而产生一个个体;②应用前述全局搜索方法产生 50%(δ−1)个个体;③从GA 解中选取最好的 50%(δ−1)个个体。从 δ个个体中选取最大完工时间最小的个体作为领飞鸟,其余均为跟飞鸟,若跟飞鸟与领飞鸟相同,则将领飞鸟通过基于机器最短处理时间的多点变异或邻域搜索结构 N1(Lmax=2)产生新跟飞鸟;若新跟飞鸟与其余跟飞鸟相同,则对新跟飞鸟继续应用邻域搜索结构 N1进行更新,直至产生与其余跟飞鸟不同的新跟飞鸟。 3)领飞鸟进化。随机产生[1,6]之间的一个整数r,若r=1,令Lmax=2,对领飞鸟执行 N1;若r=2,则执行 N2;若r=3,令ηmax=1,执行 N3;若r=4,令Lmax=4,执行 N1;若r=5,令ηmax=2,执行N3;若r=6,令Lmax=6,执行 N1。该过程往复o次产生领飞鸟的o个邻域解,若其中的最佳解优于当前领飞鸟,则更新领飞鸟,取其余(o−1)个邻域解中的最佳解加入共享邻域解集XL和XR。 4)右侧跟飞鸟进化。对右侧队列中每个个体g,执行与3)相同的邻域搜索过程产生(o−1)个邻域解,构成集合DR,找到XR∪DR内的最佳解,若其优于当前解,则更新跟飞鸟,清空XR,从XR∪DR未用的解集中选择最好的邻域解加入XR。 5)左侧跟飞鸟进化。对左侧队列中每个个体g,仍采用与3)相同的邻域搜索过程产生(o−1)个邻域解,构成集合DL,若XL∪DL内最佳解优于当前解,则更新跟飞鸟,清空XL,将XL∪DL未用的解集中最好的邻域解加入XL。 6)G1=G1+1,若G1 7)领飞鸟更新。若 α=1,将左侧队列的第一个跟飞鸟作为新领飞鸟,将原领飞鸟移至左侧队列末端,令 α=0;否则,将右侧队列的第一个跟飞鸟作为新领飞鸟,把原领飞鸟移至右侧队列末端,令 α=1。 首先,考虑本文研究的问题是含不相关机的HFSMO,其不仅与工件的处理序列有关,还与工件在每道工序的机器分配相关,因此本文设计基于机器号的编码方案,在解码时采用最短处理时间和先进先出规则确定工件处理序列;采用考虑机器处理时间的全局搜索产生一个个体,用随机程序生成剩余(e−1)个个体以生成种群规模为e的初始种群;计算适应度,根据轮盘赌法选择个体生成新种群;对新种群根据自适应更新策略计算交叉概率 ξ及变异概率 ψ,以此执行交叉和变异操作,得到遗传进化后的最佳解并记录历史最佳解。最后,当最佳解T次没变时,按照基于3 种邻域搜索结构的候鸟优化产生新解,若新解优于历史最佳解,则更新历史最佳解,否则保持原解不变,重复上述过程直至满足算法的停止标准。 综上所述,所研究的GMBOA 执行如下: 1)设置种群规模e,最大迭代数 β和累计数T,令Z∗=F,λ=1,t=1; 2)若 λ>β或CPU 达到最大运行时间,程序停止,输出最佳解;否则,执行3); 3)结合随机程序和全局搜索产生初始种群; 4)计算每个个体的适应度值,使用轮盘赌选择法获取适应度值高的个体; 5)根据交叉概率ξ,从单点交叉和均匀两点交叉2 种方式随机选择1 种生成新个体; 6)根据变异概率 ψ,随机执行基于随机机器选择的单点变异或基于机器最短处理时间的多点变异; 7)若当前迭代得到的最佳解Zλ≠Z∗,Z∗=min{Zλ,Z∗},t=1,λ=λ+1,转至2);否则,t=t+1,执行8); 8)若t=T,执行9),否则,λ=λ+1,转至2); 9)调用候鸟优化算法,若得到的最佳解优于Z∗,更新Z∗,否则,保留Z∗不变;t=1,λ=λ+1,转至2)。 本文所提的遗传候鸟优化算法将全局搜索、自适应遗传算法和候鸟优化相结合,为了验证所提出的算法性能,从传统算法、与其他算法结合的混合算法、解码规则、已发表的文献的算法4 个角度选择传统遗传算法(traditional genetic algorithm,TGA),结合3 种领域搜索结构候鸟优化算法(migrating birds optimization &neighborhood search,MBO&NS)、基于最长处理时间规则解码的遗传候鸟优化算法(genetic migrating birds optimization algorithm L,GMBOAL)、结合局域搜索的自适应遗传算法(adaptive genetic algorithm &local search,AGA&LS)与文献[30]的改进人工蜂群算法(improved artificial bee colony,IDABC)进行对比。采用Matlab R2014b 进行编程,在CPU 为Inter Core i5-5200U,内存为4 GB,主频2.2 GHz 的微机上运行。 为公平比较TGA、MBO&NS、GMBOAL、AGA&LS、IDABC 和GMBOA 这6 种算法,TGA中的 ξ 和 ψ的取值通过仿真实验得到最佳的一组设置,即 ξ=0.8 和 ψ=0.2;GMBOAL、AGA&LS 和GMBOA 中的 ξmax、ξmin、ψmax和 ψmin的取值是通过仿真实验得到最佳的一组设置,即ξmax=0.9、ξmin=0.5、ψmax=0.2 和ψmin=0.02;参考文献[22],并经过仿真实验测试GMBOA 中的 δ=31、γ=10、Gmax=10、o=3;基于GA 的4 种算法和IDABC 的种群规模e=100;由于MBO&NS 的种群规模必须为奇数,所以其种群规模e=101;IDABC 的参数与文献[30]的设置相同,最大迭代数 β=100,最大CPU 时间为720 s;考虑到GA 的运行时间较短,将MBO&NS、GMBOAL、AGA&LS、IDABC 和GMBOA 的停止时间设为TGA 运行100 次所需时间。 问题产生如下:n={20,30,40,50,80,100,120,150},h={5,10,15,20},ms=5。借鉴Dios 等[7-8]关于忽略工序比例的设定,将本文的忽略工序比例p分别取为20%、40%和60%。每个工件在同一道工序不同机器上的处理时间Pjks不同且满足[1,99]之间的均匀分布。 参数{n,h,p}的不同组合产生96 组问题规模,每种规模随机运行10 个实例,取10 次测试结果的平均值作为对应规模问题的测试结果。 定义相对偏差为 由于本文所提的算法迭代100 次的CPU 时间略长,为在较短的运行时间内测试所提算法的有效性,兼顾算法对比的公平性,将TGA 迭代100次所需的时间作为对比算法MBO&NS、GMBOAL、AGA&LS、IDABC 和所提出算法GMBOA 的停止条件,以此对比算法的性能,所以表1~6 列出的CPU 时间为TGA 迭代100 次的时间。表1~6 列出了5 种算法求解不同规模问题的实验结果。 表1 忽略工序比例为20%时中小规模问题的测试结果Table 1 Testing results for small and medium scale problems with the proportion 20% of missing operations 续表 1 表2 忽略工序比例为20%时大规模问题测试结果Table 2 Testing results for large scale problems with the proportion 20% of missing operations 表3 忽略工序比例为40%时中小规模问题测试结果Table 3 Testing results for small and medium scale problems with the proportion 40% of missing operations 续表 3 表4 忽略工序比例为40%时大规模问题测试结果Table 4 Testing results for large scale problems with the proportion 40% of missing operations 表5 忽略工序比例为60%时中小规模问题测试结果Table 5 Testing results for small and medium scale problems with the proportion 60% of missing operations 续表 5 表6 忽略工序比例为60%时大规模问题测试结果Table 6 Testing results for large scale problems with the proportion 60% of missing operations 从表1~6 可知: 1)当p=20%时,对于中小规模问题,在平均CPU 时间75.63 s 内,由TGA、MBO&NS、GMBOAL、AGA&LS、IDABC 和GMBOA 得到的平均目标值分别为479.1、478.4、403.2、391.8、412.3、381.5。GMBOA 得到的目标值较TGA 改进25.86%,较MBO&NS 改进25.30%,较GMBOAL 改进6.46%,较AGA&LS 改进3.05%,较IDABC 改进8.91%。 对于大规模问题,在平均CPU 时间166.81 s内,由TGA、MBO&NS、GMBOAL、AGA&LS、IDABC 和GMBOA 得到的平均目标值分别为917.1、885.0、761.6、738.7、740.9、723.1。GMBOA 的目标值较TGA 改进26.68%,较MBO&NS 改进22.84%,较GMBOAL 改进6.05%,较AGA&LS 改进2.00%,较IDABC 改进3.34%。 从平均性能来看,对于不同规模问题,在总平均时间121.22 s 内,TGA、MBO&NS、GMBOAL、AGA&LS、IDABC 和GMBOA 的平均目标值分别为698.1、681.7、582.4、565.3、576.6、552.3。GMBOA的目标值较TGA 改进26.27%,较MBO&NS 改进24.07%,较GMBOAL 改进6.26%,较AGA&LS 改进2.53%,较IDABC 改进6.13%。整体来看,在相同CPU 时间内,GMBOA 的表现明显优于TGA、MBO&NS、GMBOAL、AGA&LS、IDABC。 2)当p=40%时,对于中小规模问题,在平均CPU 时间70.15 s 内,由TGA、MBO&NS、GMBOAL、AGA&LS、IDABC 和GMBOA 得到的平均目标值分别为368.3、363.1、305.9、303.9、320.1、293.0。GMBOA 的目标值较TGA 改进26.12%,较MBO&NS 改进23.53%,较GMBOAL 改进4.83%,较AGA&LS 改进3.82%,较IDABC 改进9.34%。 对于大规模问题,在平均CPU 时间151.07 s内,由TGA、MBO&NS、GMBOAL、AGA&LS、IDABC 和GMBOA 得到的平均目标值分别为685.0、658.2、561.7、551.8、555.8、537.5。GMBOA 的目标值较TGA 改进26.74%,较MBO&NS 改进22.90%,较GMBOAL 改进5.04%,较AGA&LS 改进3.08%、较IDABC 改进4.39%。 从平均性能来看,对于不同规模问题,在总平均时间110.61 s 内,TGA、MBO&NS、GMBOAL、AGA&LS、IDABC 和GMBOA 的平均目标值分别为526.7、510.7、433.8、427.9、438.0、415.3。GMBOA的目标值较TGA 改进26.43%,较MBO&NS 改进23.22%,较GMBOAL 改进4.94%,较AGA&LS 改进3.45%,较IDABC 改进6.87%。因此,GMBOA比TGA、MBO&NS、GMBOAL、AGA&LS、IDABC 产生了较好的解。 3)当p=60%时,对于中小规模问题,在平均CPU 时间63.86 s 内,由TGA、MBO&NS、GMBOAL、AGA&LS、IDABC 和GMBOA 得到的平均目标值分别为264.2、251.9、212.2、216.8、233.5、207.5。GMBOA 的目标值较TGA 改进27.12%,较MBO&NS 改进20.30%,较GMBOAL 改进2.39%,较AGA&LS 改进5.09%,较IDABC 改进13.43%。 对于大规模问题,在平均CPU 时间135.28 s内,由TGA、MBO&NS、GMBOAL、AGA&LS、IDABC 和GMBOA 得到的平均目标值分别为468.3、439.1、371.4、374.6、376.0、360.8。GMBOA的目标值较TGA 改进29.83%,较MBO&NS 改进21.14%,较GMBOAL 改进3.16%,较AGA&LS 改进4.29%、较IDABC 改进4.97%。 虽然小规模问题20×10、20×15 和20×20 的3 个实例中GMBOA 的目标值略差于AGA&LS或GMBOAL,但随着问题规模的增大,GMBOA得到的解的质量一致优于其他5 种算法。 从平均性能来看,对于不同规模问题,在总平均时间99.57s 内,TGA、MBO&NS、GMBOAL、AGA&LS、IDABC 和GMBOA 的平均目标值分别为366.3、345.5、291.8、295.7、304.8、284.2。GMBOA的目标值较TGA 改进28.48%,较MBO&NS 改进20.72%,较GMBOAL 改进2.78%,较AGA&LS 改进4.69%,较IDABC 改进9.20%。因此,GMBOA表现最好,尤其是对于大规模问题。 4)综上可知,在相同CPU 时间内,虽然当忽略工序比例较高时GMBOA 求解小规模问题的一些实例的表现略差于其他算法,但平均性能均优于TGA、MBO&NS、GMBOAL、AGA&LS、IDABC。 本文研究了含忽略工序和不相关并行机的混合流水车间调度问题,以最小化最大完工时间为目标建立了整数规划模型,进而结合全局搜索、自适应遗传算法和候鸟优化提出一种遗传候鸟优化算法以获取近优解。首先,设计基于机器号的编码方案,采用全局搜索和随机程序生成初始种群,然后执行随迭代进化过程而调整的自适应交叉和变异操作,从而得到改进的GA 解,引入基于3 种邻域结构的候鸟优化算法扩大解的搜索空间以更新GA 解。大量随机数据的仿真实验证明所提遗传候鸟优化算法能够在相同的CPU 时间内得到满意的近优解。未来研究可将所提算法推广到多目标HFSMO 问题或尝试其他近似算法(如禁忌搜索、人工蜂群等)求解含不相关并行机的HFSMO 问题。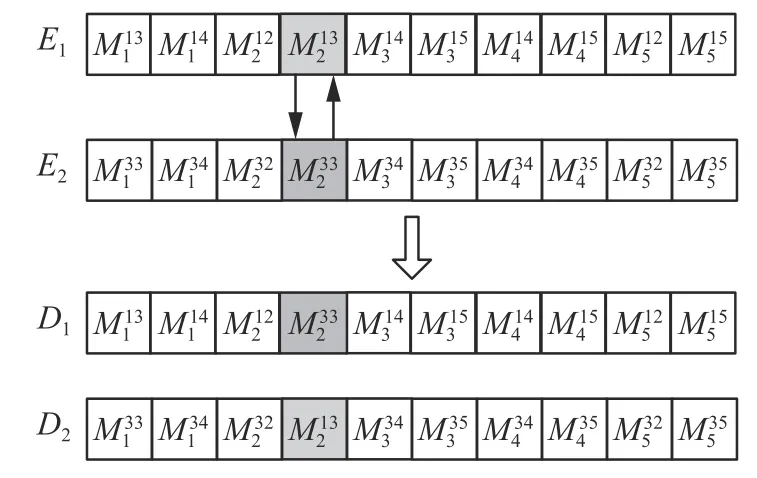


2.3 变异操作


2.4 基于3 种邻域搜索结构的候鸟优化
2.5 遗传候鸟优化算法流程
3 仿真实验
3.1 参数设置
3.2 数据实验与结果分析










4 结束语

