改进EEMD-GRU 混合模型在径流预报中的应用

刘扬，王立虎，杨礼波，刘雪梅

（华北水利水电大学 信息工程学院,河南 郑州 450046）

河川径流作为水循环的关键节点，对其进行精确预报具有重要意义。变化环境下径流的波动系数不断加大，极端气候背景下的径流趋势呈现更大的波动性，给径流的准确预报提出了更高的要求。如何根据不同流域，提出更加稳定、高效的预报模型，具有重要的理论意义和应用价值。

目前，以物理认识为基础的机理驱动模型和以统计科学为基础的数据驱动模型在径流预报领域取得了一定的进展。以气象数据作为输入，利用半分布式水文模型对径流进行预测，并以异常相关系数作为评估指标，实验结果表明，确定性预测精度较高[1]。将分布式水文模型和气象遥相关分析相结合，采用水文模型提供初始条件，利用遥相关指数确定气象输入，开展流域水库入库径流的长期预测[2]。然而，机理驱动模型往往存在可解释性差，主观干扰因素众多等问题。数据驱动模型可以有效缓解机理模型带来的不足[3-6]。例如，以支持向量回归(support vector regression,SVR)模型预测集水区洪水发生概率，结果表明，SVR 模型对于提前1～3 h的预测具有令人满意的预测性能[7]。利用自适应神经模糊推理系统（adaptive neuro-fuzzy inference system,ANFIS）对区域径流进行预测。结果表明，ANFIS 模型的平均绝对误差优于其他模型[8]。然而，以统计科学为基础的数据模型往往存在预测精度低，可解释性差等问题。混合模型可有效缓解数据模型的不足。结合人工神经网络（artificial neural network,ANN）模型和Muskingum-Cunge 方法，进而构建一种基于BR-ANN 的洪水预报模型。研究区的验证对比结果表明，BR-ANN 模型具有优越的综合预测能力[9]。将 SWAT 模型与ANN 模型结合并用于区域径流预测，结果表明SWAT-ANN 的预测精度优于SWAT 模型[10]。结合经验模式分解（empirical mode decompostion,EMD）算法与长短时记忆神经网络（long short-term memory networks,LSTM），进而构建EMD-LSTM 模型。并使用均方根误差（root mean square error,RMSE）、决定系数、Willmott 一致性指数（Willmott index,WI）和Legates-McCabe 指数（legates McCabe index,LMI）作为评估标准，结果表明该方法在特大洪水年预测可靠性较高[11]。然而，EMD 方法在分解过程中往往存在模态混叠和端点效应[12-14]。

针对以上问题，本文结合改进集合经验模态分解（ensemble empirical mode decomposition,EEMD）与门控制循环单元神经网络（goted recurrent unit,GRU）构建一种基于改进EEMD 的神经网络模型（EEMD-GRU）。该模型将改进EEMD 方法和GRU 模型进行融合，同时引入并行计算思想，实现对径流的精确、高效、稳定预测。经验证，相比于结合了EMD 的SVR 模型，并行EEMD-GRU 模型表现出更加高效、可靠的性能。

1 相关理论

1.1 GRU 深度学习

GRU 基于循环神经网络。同循环神经网络相比，GRU 具有计算效率高，逻辑简单等优势[15]。其基本结构如图1 所示。

图1 GRU 神经元结构Fig.1 GRU neuron structure

GRU 的提出是为了克服RNN 无法很好地处理远距离依赖的问题，在保持了LSTM 效果的同时使结构更加简单。GRU 仅保留了重置门和更新门，即图中r(t)和z(t)，其中重置门输出矩阵rt可定义为

式中：wr为重置门的权重矩阵；σ为sigmoid 函数；h(t−1)为t−1 时刻的隐含状态；x(t)为t时刻输入数据。更新门输出矩阵zt可定义为

式中：wz为更新门的权重矩阵；则GRU 网络的输出可定义为

式中：Wo为输出权重矩阵；c为输出偏置[16-18]。

1.2 集合经验模态分解

EEMD 在经验模态分解的基础上，通过引入白噪声，有效消除了模态混叠现象，使得EEMD的分解结果更加具有物理意义[19-24]，集合经验模态分解的基本原理可以描述如下：

1）将正态分布的白噪声信号ni(t)加到原始信号x(t)得到信号xi(t)，定义为

xi(t)=x(t)+ni(t)

2）将加入白噪声的信号作为一个整体，然后进行经验模态分解（EMD），得到各IMF 分量，定义为

式中：cij(t)为第i次加入白噪声后分解得到的第j个IMF 分量；ri(t)是分解后的剩余分量；n为IMF 分量的个数。

3）重复1）～2），对各阶分量取平均，得到最终IMF 分量cj(t)为

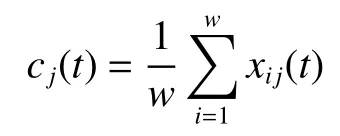
式中w为添加白噪声的次数，即总体平均数。

EEMD 的提出是解决EMD 分解过程中出现的模态混叠现象，使得在模态分解过程中可以很好地避免IMF 分量不精确等问题[25-26]。

2 径流预报方法构建

2.1 基于智能算法的端点效应改进方案

解决集合经验模态分解边界效应的方法一般是对信号进行边界拖延。本文利用极限学习算法作为模态分解端点效应的解决方案，具体步骤如下：

1）以右边界为例，选取合适的拓延步长，作为原始信号的拓延信号序列长度；

2）将原始信号划分为测试集、训练集，进而构建极限学习预测模型；

3）将原始信号右端点利用预测模型进行预测，预测信号与原始信号合并；

4）利用相同的原理拓延原始信号的左边界。

2.2 并行EEMD-GRU 径流预测方法

综合实时采集技术，以黄河流域部分干流共32 个水文站的实际水文数据作为数据支撑，进行数据清洗、分解、预测、重构等一系列操作，最终获得高精度径流预测值，进而为水库的安全运行和区域防洪减灾提供决策支持。图2 给出了并行EEMD-GRU 的数据流程图，其基本实现如下。

图2 并行EEMD-GRU 流程Fig.2 Parallel EEMD-GRU flow

1)以黄河流域部分干流为实验对象，实时采集水文站径流数据f(t)，通过数据清洗技术，对空数据、非数值型数据等非法数据进行过滤，然后对其进行归一化，其中归一化方程可定义为

式中：max(x)为样本数据的最大值；min(x)为样本数据的最小值。

2)基于带外误差理论，以目标站点为基准，将目标预测站上下游水文站径流数据作为特征x∗,对目标预测站进行特征选择。首先，将径流样本通过重复抽样的方式构建样本，训练模型，然后利用剩余样本对模型进行评估，并计算样本误差，记作E1，最后将剩余样本加入噪声，计算剩余样本的误差，记作E2，特征fi(x∗)的重要性可定义为

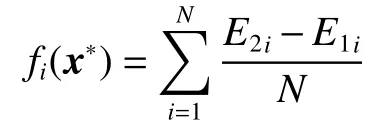
fi(x∗)值越大，表明特征x∗的重要程度越高。

3)将归一化并经过特征选择的数据首先进行边界拓延，然后进行EEMD 分解，分解为若干本征模态分量，并将各分量分别拆分为训练集和测试集；

4)对训练集与测试集进行数据划分，将过去5 d（通过实验分析，将预测集序列长度设置为5模型效果最优）设置为输入变量，分别对未来1、4、6、16、21、31 d 进行预测；

5)对预测分量进行重组，由此得到输出序列。

3 结果和分析

本文选取黄河流域2002—2019 年径流观测数据作为数据支撑，以EMD-SVR[27]和GRU[28]作为对比模型，以纳什指数(Ens)、平均绝对误差、相关误差、运行时间（run time）作为评估标准，实现对算法的可信度、稳定度、精准度和执行效率的全面评估。其中Ens纳什效率系数用于评估预测模型的可信度与稳定度。Ens取值为负无穷至1，Ens接近1，表示模式质量好，模型可信度高。相对误差和平均绝对误差分别评估实时误差与整体误差。

并行EEMD-GRU 方法及EMD-SVR 方法分别对未来1、4、6、16、21、31 d 径流深度进行预测，结果如图3 所示。

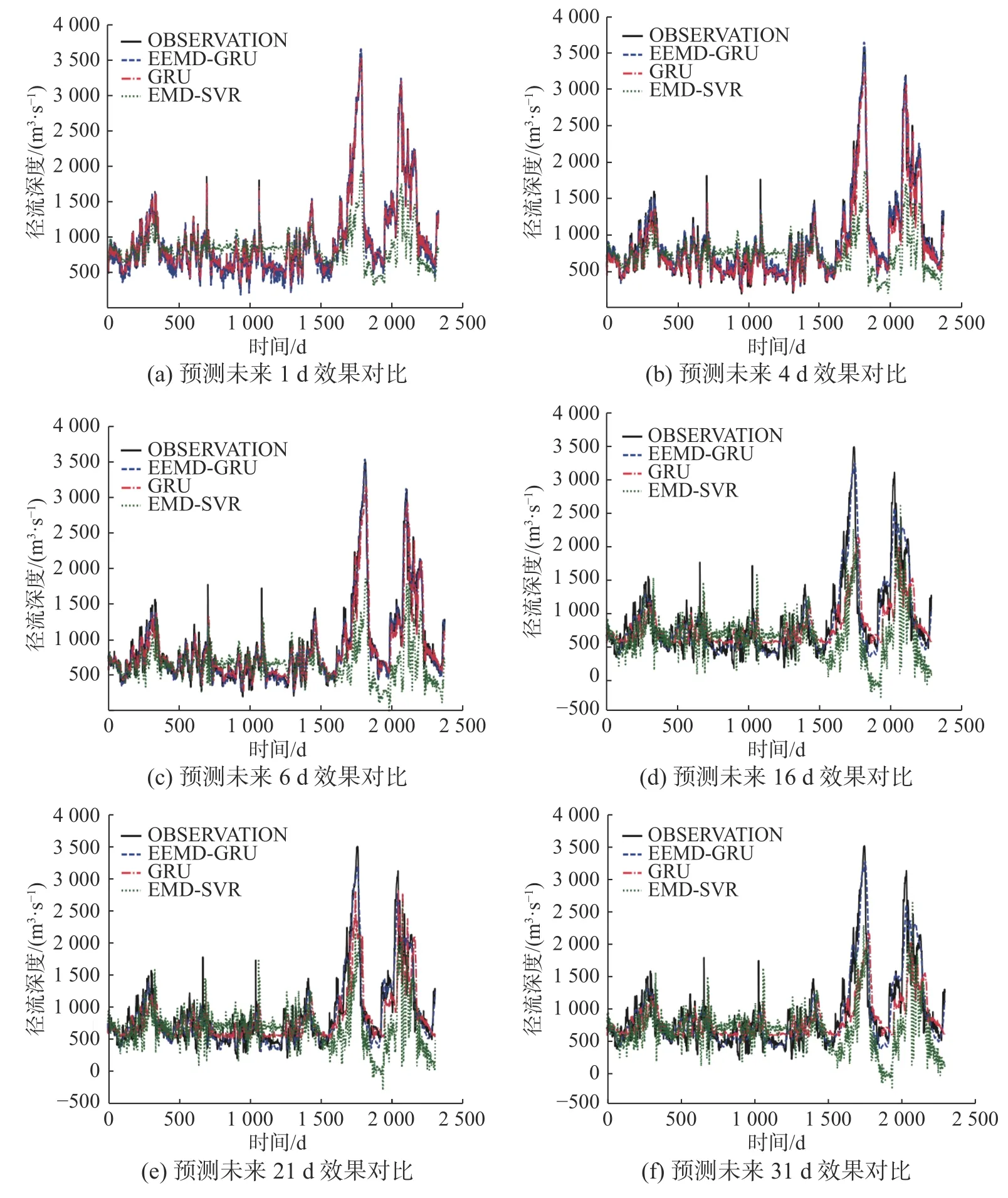
图3 不同模型不同时间尺度下的预测曲线对比Fig.3 Comparison of prediction curves under different models and different time scales

根据图3 可知，在低延时的未来预测中，EEMDGRU 与GRU 表现能力相似，但是随着预测天数的增加，EEMD-GRU 相对于GRU 和EMD-SVR 具有较高的精确度。由于EEMD 可有效提高GRU模型的鲁棒性。使得固定未来天数，调整预测序列的特征和序列长度，EEMD-GRU 相比GRU 模型稳定性高。

根据图4 可以了解到，EEMD-GRU 相对于GRU 模型和EMD-SVR 模型，预测误差更小，精度更高，且相对于其他模型更加稳定。由于EMD方法存在模态混叠和端点效应，EMD-SVR 模型预测精度最差。

图4 不同模型不同时间尺度下的相对误差对比Fig.4 Comparison of relative errors of different models and different time scales

综合表1 与图5，由于EEMD-GRU 引入了分解合成策略，有效提高了模型的非稳态信号处理能力，模型的预测精度提高，可信度增强。算法的运行时间可以作为算法运行效率的一个衡量标准，EEMD-GRU 模型相对于EMD-SVR 模型由于加入了并行计算的概念，使得模型的整体预测效率提高。

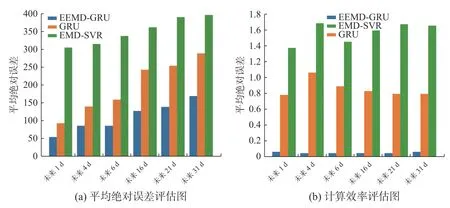
图5 智能计算模型指标评估图Fig.5 Intelligent calculation model index evaluation chart

表1 不同模型不同时间尺度下指标数值对比Table 1 Comparison of index values under different models and different time scales

续表 1

图6 反应了各个算法在预测过程中的实时可信度表现。在中长期径流预测中，预见期的增加，序列的非稳态性增强，对模型的鲁棒性要求更高。预见期为未来16 d、31 d 时，EMD-SVR 和GRU 模型相对于EEMD-GRU 模型，可信度较差。

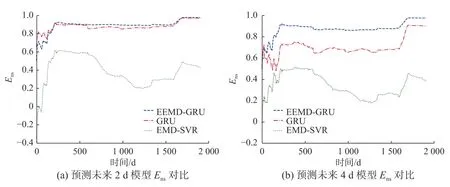
图6 智能计算模型 Ens评估图Fig.6 Intelligent calculation model Ens evaluation chart

4 结束语

本文在模态分解方法与深度学习方法的思想上，构造了并行EEMD-GRU 径流预测方法，主要结论有：

1）本文所提出的并行EEMD-GRU 模型对于不同预测步长，预测时间均有有较高的精度、可信度和预测效率，预测模型具有一定的泛化性和鲁棒性，通过与原生GRU 模型和EMD-SVR 模型的对比中发现，所构建的混合模型精准度、可信度和效率高于其他模型。

2)由于引入了EEMD 分解算法，使得混合模型整体计算性能有所下降，虽然所引入的并行计算思想可以有效解决模型计算消耗，但随之而来的的确是内存消耗问题，希望在今后的研究中更加关注模型的高性能计算，使得模型综合能力可以进一步提升。