支持向量机与神经网络相结合的板带凸度预测

刘明华，张强

（西安建筑科技大学 冶金工程学院,陕西 西安 710055）

随着社会经济的发展和科学技术的进步，板带材是工农业生产中重要的金属材料，人们对板带材的质量要求越来越高[1]。板形是板带轧制的关键技术指标，主要包括板带凸度和平直度。目前，板带凸度一直存在严重的问题，其不良凸度会直接造成巨大的资源浪费或其他潜在风险[2]。板带轧制是一个多变量、强耦合、非线性和时变性的过程，而按照传统理论方法建立的板带凸度预测模型[3]，在建模中假设和简化了轧制过程的诸多实际因素（将一个复杂非线性问题变成多个线性问题等），导致模型精确度较差，不能满足高精度轧制技术的要求[4]。因此，迫切需要一种新的方法建立具有高精度预测能力的板带凸度模型。

与传统理论方法不同，人工智能方法[5]是模拟人脑处理真实发生的过程，基于实验数据对目标值预测，可防止假设脱离实际和简化过于粗糙而产生的误差。随着人工智能技术的发展，许多学者开始将人工神经网络(ANN)[6-7]和支持向量机(SVM)[8-9]引入轧制领域。针对采用传统理论方法建立板带凸度模型考虑影响参数较少导致传统数学模型预测误差大的问题，方敏[10]提出一种BP 神经网络(BPNN)与有限元(FEM)模型相结合的方法对板带凸度进行预测，将FEM 仿真结果用于训练和测试BPNN 模型。仿真结果表明，BPNN与FEM 相结合的板带凸度预测模型的预测精度远高于传统数学模型的预测精度。针对传统BPNN预测模型存在易陷入局部极小值点和收敛速度慢等问题，朱永波等[11]采用自适应变异粒子群算法优化BPNN 模型的权值和阈值，将已优化的BPNN模型用于预测板带凸度。仿真结果表明，该模型预测效果与传统BPNN 模型相比有所改善。在以上研究中，ANN 已经广泛应用于轧制领域且该模型的预测精度高于传统数学模型的预测精度，但它也有一些不足之处。ANN 以传统统计学为基础，它的内容是样本无穷大时的渐进理论，但现实中样本往往是有限的，采用ANN 方法建立的板带凸度预测模型往往会产生过拟合现象。因此，急需一种在样本有限的情况下，也可以实现较高泛化能力的板带凸度模型。

与ANN 方法不同，SVM 是一种基于结构风险最小化原理的算法，保证了该模型具有良好的泛化能力[12]。SVM 以统计学理论为基础，根据有限的样本在模型的复杂性和学习能力之间寻求最佳折中，以期获得最好的泛化能力[13-14]。支持向量回归（SVR）是SVM 在回归条件下的应用[15]。Fei等[16]提出在样本有限的条件下，采用ANN 方法不适合建立预测模型，而采用SVR 方法建立的预测模型具有较高的泛化性能。Wu 等[17]在实验数据有限的情况下，为提高SVR 轧制力模型的预测精度，采用粒子群优化算法（PSO）优化SVR 模型参数，结果表明，PSO-SVR 模型相比SVR 和BPNN模型具有较高的预测精度，且SVR 比BPNN 模型预测精度高。综上可得，在样本数据有限的情况下，采用SVR 建立模型可以避免ANN 建立模型所产生的过拟合现象，采用PSO 算法[18]可以提高SVR 模型的预测精度，即PSO-SVR 模型具有较高的泛化能力，但另一方面PSO 算法优化参数虽可以有效保证模型参数的有效性，但板带轧制过程干扰因素较多、测量数据存在误差和数据处理不当等因素都会导致输入数据存在偏差，使PSOSVR 模型难以准确地预测板带凸度。

为提高PSO-SVR 模型的预测精度，本文提出采用BPNN 建立板带凸度偏差模型与PSO-SVR板带凸度模型相结合的方法对板带凸度进行预测。采用现场数据验证模型的预测性能，结果表明，与PSO-SVR、SVR、BPNN 和GA-SVR 模型比较，PSO-SVR+BPNN 模型具有较高的学习能力和泛化能力。

1 建立PSO-SVR 板带凸度预测模型

1.1 板凸度的基本概念

板凸度是指板带材横向的断面厚度差，即板带的中间与边部厚度之差，板凸度的计算公式为

式中：C为板带凸度；hc为中心厚度；he和he′为边部代表点厚度。

板带凸度示意图如图1 所示，其中e表示板材边部代表点距板材边上之间的距离，通常取e=25 mm或e=40 mm 处，本文分析中均取e=40 mm。

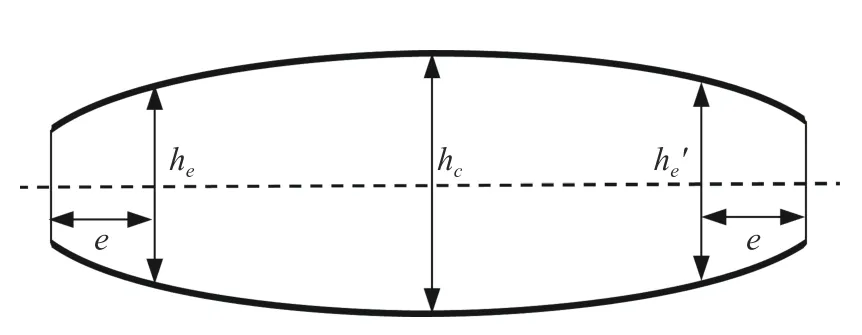
图1 板带凸度示意图Fig.1 Schematic diagram of strip crown

1.2 实验数据的采集与处理

从某中厚板厂的热轧生产线上获取670 组Q355B 板带轧制数据，作为实验样本，如表1 所示。选择轧前板材厚度H0、轧后板材厚度H1、轧前温度T0、轧后温度T1、轧前板材宽度B、轧制力F、轧制力矩P、轧制速度v、摩擦系数 µ和轧前板材凸度C0作为输入变量，并选择轧后板材凸度C1作为输出变量。

表1 热轧实验数据Table 1 Experimental data of hot rolling

从工厂收集的样本包含异常和嘈杂的数据，会降低模型的准确度，为获得真实的分析结果，利用T 检验准则处理样本，舍去34 组异常数据，最终选择636 组数据作为实验数据，其中500 组数据作为训练集，剩余数据作为测试集。不同的影响因素通常具有数量级差异，将会降低模型的预测精度和训练速度。在建模之前，实验数据进行归一化为[−1,1]，归一化公式为

式中 max(xi)和 min(xi)分别为序列的最大值和最小值，i=1,2,···,l。

1.3 SVR 理论

SVR 是一种机器学习方法[15]，SVR 的基本思想是通过 φ(x)将非线性的低维不可分割数据映射到高维特征空间，并在该特征空间中执行线性SVR。

SVR 函数可以表述为

式中：f(x)为预测值；w为惯性权值；w·x为w和x的内积；b为阈值。

引入两个松弛变量 ξi和 ξi∗，优化问题可变成：

式中：C为惩罚因子；ξi和 ξi∗为松弛变量；ε为不敏感损失参数。

引入拉格朗日函数和基于强对偶关系，并将核函数K(xi,x)=φ(xi)·φ(x)代入化简，式(1)可以重写为

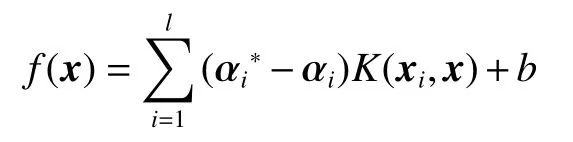
式中 αi和 αi∗是拉格朗日乘子向量。

选择核函数对于SVR 至关重要，它将直接影响数据样本的非线性映射。为了获得更好的泛化能力，选择RBF 核函数用于SVR 模型，公式为

K(xi,x)=exp(−g|xi−x|2)

式中g是RBF 核函数的参数。

C和g是影响SVR 模型预测精度的重要参数，选择PSO 算法优化二者的最佳组合，以确保模型的最佳性能。

1.4 PSO 算法优化SVR 模型参数

PSO 算法是一种基于群体智能原理的随机优化算法，由Kennedy 和Eberhart 在1995 年提出[19]。PSO 算法受到鸟类觅食行为的启发并应用到解决优化问题[20]，粒子群在高维空间中随机分布并跟踪个体极值和种群极值不断更新自己的位置和速度，使其向全局最优粒子的位置靠近，并试图在空间中搜索最优参数（C,g）[21]。

2 建立PSO-SVR+BPNN 板带凸度预测模型

2.1 BPNN 板带凸度偏差预测模型

ANN 通过调整节点之间的关系来处理信息，具有强大的自学习能力。本文ANN 采用常用的BPNN 模型，模型结构由一个输入层、单或多隐含层和一个输出层组成[22]。利用训练集检验SVR模型的误差，并将误差数据集用于训练BPNN 模型。因此，在本节选择轧后板带凸度的预测偏差XC作为BPNN 模型的因变量，BPNN 与SVR 模型的自变量保持一致，即BPNN 模型输入层节点数为10，输出层节点数为1。在相同条件下，使用多隐含层所获得的预测结果并未比单隐含层网络拟合效果好，所以本文选择单隐含层进行建模，通过经验公式和试凑法[23]确定单隐含层节点数为6，输入层到隐含层的网络权值为 ωij，隐含层到输出层的网络权值为 ωjk，由以上参数绘制BPNN 的拓扑结构如图2。

图2 BPNN 拓扑结构Fig.2 Topological structure of BPNN

2.2 PSO-SVR+BPNN 板带凸度预测模型

在实际应用中，板带轧制过程干扰因素较多，测量数据存在误差和数据处理不当，这些问题都会导致输入数据存在偏差，使PSO-SVR 模型难以准确地描述板带凸度变化趋势。为提高该模型的预测精度，提出了将PSO-SVR 板带凸度预测模型和BPNN 板带凸度偏差模型相结合的方法对板带凸度进行预测。该方法的主要思想是在无外界因素干扰的情况下，经过PSO 算法优化的SVR 模型具有良好的泛化能力，能够很好地反映板带凸度变化的主要趋势，用它来预测板带凸度的主值；BPNN模型反映扰动因素对板带凸度的影响，用它来纠正板带凸度的偏差。BPNN 修正PSO-SVR 模型的预测误差，从而使PSO-SVR 模型预测误差弱化，将两者的优势进行组合，可以得到最佳的预测效果，PSO-SVR+BPNN 模型预测板带凸度公式为

式中：c2′为 PSO-SVR+BPNN 模型的预测值；c1′为PSOSVR 模型的预测值；xc为BPNN 模型的预测偏差。

本文所提出的PSO-SVR+BPNN 模型的建模过程如图3 所示。

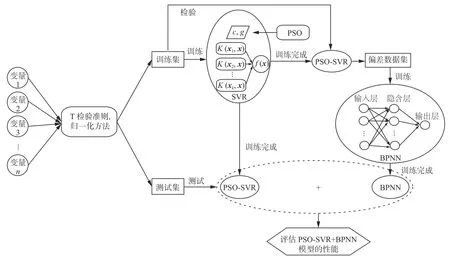
图3 PSO-SVR+BPNN 模型的建模流程Fig.3 Modeling process of PSO-SVR+BPNN model

从工厂获取实验数据，并利用T 检验准则和归一化方法预处理实验数据，使其消除异常数据和数量级差异。其次，采用PSO 算法优化SVR 模型参数，利用训练集检验建立PSO-SVR 模型时所产生的误差，并将误差数据集用于训练BPNN 模型，将PSO-SVR 与BPNN 模型相结合进行预测板带凸度。最后，利用测试集测试PSO-SVR+BPNN模型的预测精度，并采用决定系数(R2)、根均方误差(RMSE)、平均绝对误差(MAE)和平均绝对百分比误差(MAPE)用于评估模型的综合性能，公式为

式中：y′为模型的预测数据集；y为模型的目标数据集。

3 实验结果与分析

3.1 PSO-SVR+BPNN 模型与PSO-SVR、SVR 和BPNN 模型比较

为了体现PSO-SVR+BPNN 模型综合性能的优越性，采用PSO-SVR、SVR 和BPNN 建立板带凸度模型，利用R2、RMSE、MAE 和MAPE 评估模型的综合性能。在训练集和测试集上，4 种模型预测值与目标值的回归结果，如图4 所示。从图4可得，采用SVR 的3 种模型的回归性能明显优于BPNN 模型。在训练集和测试集上，BPNN 模型的R2不高于0.995，而基于SVR 的3 种模型的所有R2均高于0.997，这充分说明了基于SVR 的3 种模型比BPNN 模型的预测精度高。由此可见，基于SVR 板带凸度预测模型具有较高的泛化能力。

图4 PSO-SVR+BPNN、PSO-SVR、SVR 和BPNN 模型预测值与目标值的回归结果Fig.4 Regression results of predicted values and target values of PSO-SVR+BPNN、PSO-SVR、SVR and BPNN models

图4 描述了在训练集和测试集上，PSO-SVR与SVR 模型相比具有较大的R2值，即PSO-SVR比SVR 模型预测性能好。同理可得，与PSO-SVR相比，PSO-SVR+BPNN 模型具有较好的预测性能。实验结果表明，采用PSO 算法优化SVR 模型参数，可以提高SVR 模型的学习能力和泛化能力；利用BPNN 模型纠正PSO-SVR 模型的预测偏差，可以提高PSO-SVR 模型的学习能力和泛化能力。

图5 描述了不同模型预测值与目标值的比较。从图5 中可得，基于SVR 的3 种模型和BPNN模型有较高预测精度，但无法直接地区别各模型的预测精度，因此分别从两个数据集上任意选取五个连续的样本点测试模型的预测性能，如表2所示。表2 清楚地显示PSO-SVR+BPNN 模型与PSO-SVR、SVR 和BPNN 模型之间的预测精度差异。在训练集和测试集上，PSO-SVR+BPNN 模型预测值的相对误差在2% 以内；PSO-SVR、SVR和BPNN 模型预测值中大部分数据点的相对误差分别在5%、8%和11%以内。以上结果表明，SVR与BPNN 模型相比具有较高的预测性能，但低于PSO-SVR 模型的预测性能；与PSO-SVR、SVR 和BPNN 模型相比，PSO-SVR+BPNN 模型的学习能力和预测精度最高。

图5 PSO-SVR+BPNN、PSO-SVR、SVR 和BPNN 模型预测值与目标值的比较Fig.5 Comparison of predicted values and target values for PSO-SVR+BPNN、PSO-SVR、SVR and BPNN models

表2 部分样本数据下不同模型的相对误差Table 2 Relative error of different models under partial sample data

续表 2

通过RMSE、MAE 和MAPE 测试各模型的综合性能。表3 列出了各模型在训练集和测试集上3 种误差指标的计算值，图6 是从计算结果中得出误差分布的直方图。表3 和图6 清楚地表明，在训练集和测试集上，PSO-SVR+BPNN 模型的RMSE、MAE 和MAPE 指标最小，分别为0.004 2和0.001 2、0.000 9 和0.000 8、2.371 5%和2.690 3%。PSO-SVR+BPNN 模型的MAPE 在2.7% 以内；PSO-SVR、SVR 和BPNN 模型的MAPE 分别在7.1%、16.4%和18.4%以内。以上结果与表2 结果保持一致，PSO-SVR+BPNN 模型与其他3 种模型相比具有最佳的学习能力和泛化能力，再次验证了PSO-SVR+BPNN 板带凸度模型的优越性。

图6 不同模型的误差直方图Fig.6 Error histograms of different models

表3 不同模型的性能统计分析Table 3 Performance statistical analysis of different models

此外，对影响PSO-SVR+BPNN 板带凸度模型性能的主要因素进行定量分析，将未优化SVR 模型参数C和g，设定为模型1；未优化BPNN 模型隐含层节点数，设定为模型2；未删除异常数据，设定为模型3；以上因素全部考虑，设定为模型4，采用R2指标评价各模型的预测性能，实验结果如表4 所示。从表4 可以看出，在训练集和测试集上，模型3 的R2最小，模型2 的R2相对较小，而模型1 的R2相对较大。因此，异常数据对模型性能的影响最大，其次，隐含层节点数对模型性能的影响较小，而参数C和g对模型性能的影响最小。

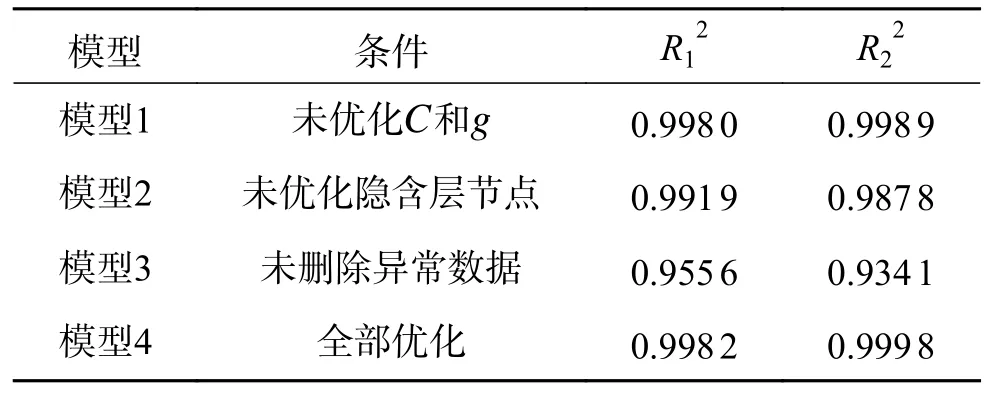
表4 不同条件下模型性能的影响Table 4 Impact of model performance based on different conditions

3.2 PSO-SVR+BPNN 模型与GA-SVR 模型比较

遗传算法（GA）[24]是一种通过模拟自然进化过程搜索最优解的方法，具有较高的全局优化能力、通用性强且适用于并行处理的优点，常常被使用在模型参数优化方面。本节采用GA 算法优化SVR 参数，建立GA-SVR 板带凸度预测模型，并将PSO-SVR+BPNN 与GA-SVR 模型进行综合性能对比。

PSO 与GA 算法相同的参数设置：种群规模20，终止迭代次数20，C和 g取值(0.01,100)和(0,1)。特有参数设置：对于PSO 算法，惯性权值为1/(2ln2)，加速因子为ln2+0.5；而GA 算法，交叉概率为0.4 和变异概率为0.1。在相同条件下，GA-SVR与PSO-SVR+BPNN 模型在训练集和测试集上预测值的比较，如图7 所示。图7 中显示两个模型都具有较高的预测精度。为了直观地分析2 个模型之间的性能差异，采用RMSE、MAE 和MAPE评估模型的预测性能，如表5 所示。在训练集和测试集上，PSO-SVR+BPNN 模型的3 个误差指标均明显低于GA-SVR 模型的3 个误差指标。以上结果充分证明，PSO-SVR+BPNN 比GA-SVR 模型具有更高的学习能力和预测精度。

图7 PSO-SVR+BPNN 和GA-SVR 模型预测值与目标值的比较Fig.7 Comparison of predicted values and target values for PSO-SVR+BPNN and GA-SVR model

表5 不同模型的性能统计分析Table 5 Performance statistical analysis of different models

此外，运算时间是判断模型是否能在线应用的一个重要指标。图8 描述PSO-SVR+BPNN 和GA-SVR 模型在不同迭代条件下的运算时间。从图8 中可得，在相同迭代次数条件下，GA-SVR 模型的运算时间明显高于PSO-SVR+BPNN 模型。随着迭代次数的增加，GA-SVR 模型比PSOSVR+BPNN 模型运算时间的增长趋势更显著，因此PSO-SVR+BPNN 模型更适合热轧生产过程中板带凸度的在线预测。

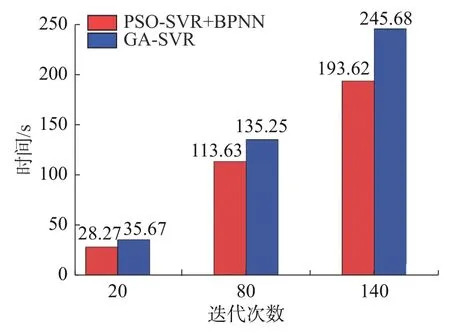
图8 PSO-SVR+BPNN 模型与GA-SVR 模型运算时间比较Fig.8 Comparison of computing time for PSO-SVR+BPNN and GA-SVR model

4 结束语

为了提高热轧生产过程中板带凸度的预测精度，本文建立了PSO-SVR 模型与BPNN 模型相结合的混合模型PSO-SVR+BPNN 对板带凸度进行预测。实验结果表明：1）基于SVR 板带凸度预测模型具有很高的泛化能力；2）在实验数据有限的情况下，基于SVR 模型比BPNN 模型更适合作为板带凸度预测模型；3）采用BPNN 模型与PSOSVR 模型相结合的方法可以提高PSO-SVR 模型的学习能力和泛化能力；4）PSO-SVR+BPNN 模型比PSO-SVR、SVR、BPNN 和GA-SVR 模型具有较高的学习能力和泛化能力，并且比GA-SVR 模型更适合热轧生产过程中板带凸度的在线预测。