借问考生错何处,题意暗指素养故
周颖颖

摘要:本文通过错例示范法,研究立体图形中的最短路径问题,分析学生产生错误的本质原因,从而启发教师在平时教学过程中,从五个方面重视学生数学学科素养的培养.
关键词:错例示范;最短路径;数学素养;
原题呈现与试题分析
【原题呈现】
在几何体表面上,蚂蚁怎样爬行路径最短?
如图①,圆锥的母线长为12cm,B为母线OC的中点,点A在底面圆周上,的长为4πcm,在图②所示的圆锥的侧面展开图画出蚂蚁从点A爬行到点B的最短路径,并标出它的长(结果保留根号).
图③中的几何体由底面半径相同的圆锥和圆柱组成,O是圆锥的顶点,点A在圆柱的底面圆周上. 设圆锥的母线长为l,圆柱的高为h.
①蚂蚁从点A爬行到点O的最短路径的长为_______(用含h,l的代数式表示).
②设的长为a,点B在母线OC上,OB=b,圓柱的侧面展开图如图④所示,在图中画出蚂蚁从点A爬行到点B的最短路径的示意图,并写出求最短路径的长的思路.
【试题分析】
本题是立体图形表面爬行的最短路径问题,需要学生将立体图形转化成平面图形,第一问也正是为这一点做好铺垫:将立体图形展开成平面图形,继而在平面图形上找到最短路径. 第二问是在组合的立体图形表面找最短路径,难点是将立体图形展开成平面图形,这里需要学生具有类比联想的能力:圆锥的平面展开图是一个扇形和一个圆,它们通过一个点连接,从而可以类比出本题的组合图形的平面展开图.而且还考察了学生的临界思想:展开后找最短路径转化成两条线段的和的最小值,当三点共线时最小.本题对学生的综合能力要求高,考察了学生的转化思想、化归思想以及临界思想.
二、解法与思路分析
解(1)如图①,AB即为最短路径.
(2)①h+l
②如图②,AB即为最短路径.
求最短路径的长的思路如下:
设切点为E,作AF⊥EC,连接OE,作BG⊥OE.
第一步,设EF=x,则=EC=a-x,于是∠EOC= .
第二步,解Rt∆OBG可得BG=b·cos∠EOC ,OG=b·sin∠EOC ,
于是EG=l-b·cos∠EOC
第三步,由ΔAEF∽ΔEBG得,可求出x的值.
第四步,根据勾股定理求出AE和BE,则最短路径的长为AB=AE+BE.
特别地,若点B在O或者C处,易得最短路径长.
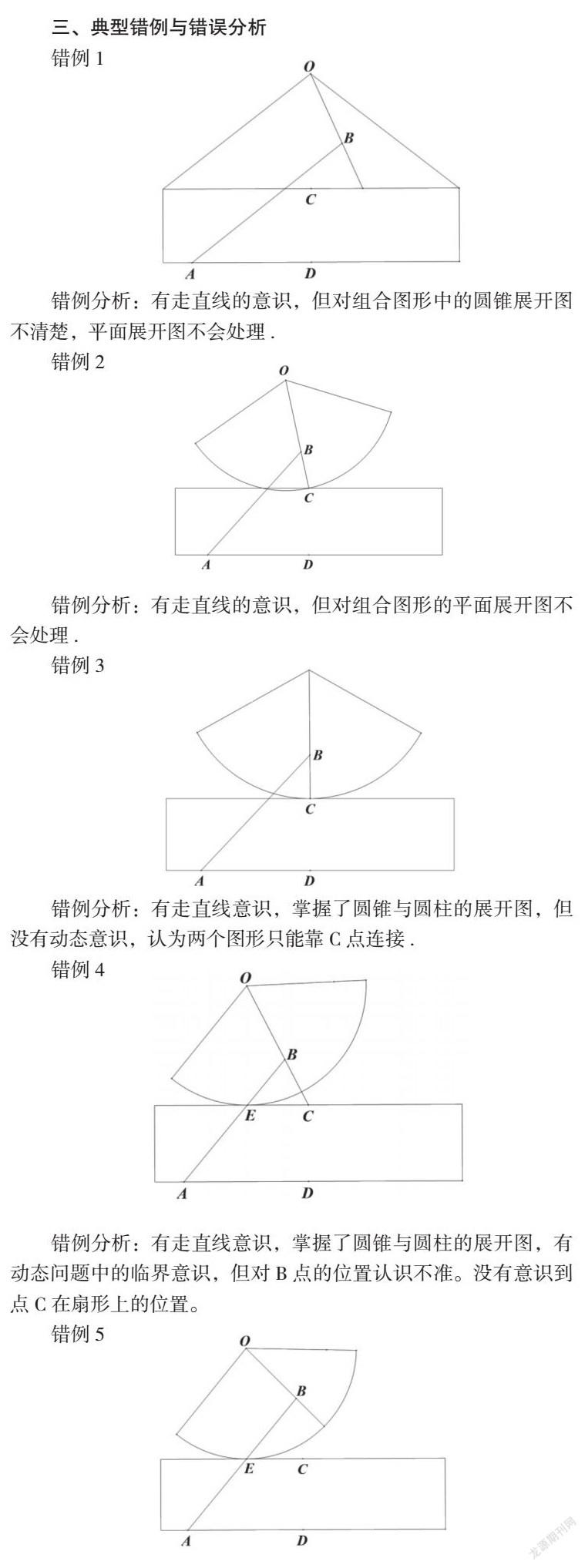
三、典型错例与错误分析
错例分析:有走直线的意识,但对组合图形中的圆锥展开图不清楚,平面展开图不会处理.
错例分析:有走直线的意识,但对组合图形的平面展开图不会处理.
错例分析:有走直线意识,掌握了圆锥与圆柱的展开图,但没有动态意识,认为两个图形只能靠C点连接.
错例分析:有走直线意识,掌握了圆锥与圆柱的展开图,有动态问题中的临界意识,但对B点的位置认识不准。没有意识到点C在扇形上的位置。
错误分析:有走直线意识,掌握了圆锥与圆柱的展开图,有动态问题中的临界意识,没有意识到点C在扇形上与点E构成的弧长等于EC.
四、教学启示
(一)在几何教学中,培养学生“降维式”思维方式
初中生更擅长解决平面几何问题,该题的难点是给出的图形是由圆柱与圆锥组成的立体几何问题.如何把蚂蚁从点A爬行到点B的最短路径的立体几何问题,转化为平面几何问题,是一大难点.大多数学生均能想到将立体几何展开,可这道题与以往的立体几何平面展开图不同:圆柱和圆锥的展开图如何合成一个图.这需要借鉴立体图形的平面展开图获得的经验产生联想.
(二)经历由“静”到“动”的思维过程,培养学生化归与转化的数学思想
在几何问题中,很多看似静态的问题,在尝试、分析、挖掘题目后其实本质是一个动态问题.如本题:圆锥的展开图扇形与圆柱的展开图矩形是通过一个点来连接的,这个点是任意的,这就相当于可以将扇形在矩形上滚动,是一个动态问题,在这个动态问题中找出最值.在平时的教学中,碰到此类问题,要鼓励学生去挖掘、去分析、去化归,以获取这类经验.
(三)利用最近发展域,培养学生类比猜想能力
两点之间线段最短,学生对这个结论是比较熟悉的。本题问的是蚂蚁从点A爬行到点B的最短路径,学生根据经验,猜想:线段最短,进而会去寻求何时为线段,从而想到使得点A,E,B在一条直线上时.至于猜想正确与否,题目中并没有要求证明,因为要用到高中的导数知识.“猜想——验证”是数学学习的重要方法,有时候猜想比验证更重要,如果在平时的教学过程中,有意识地利用学生已有的知识,引导其进行类比猜想,那初中生的猜想能力以及创新能力均能得到有效地发展,为后期的学习打下坚实的基础.
(四)强化临界意识,培养学生特殊与一般的数学思想
在教学中,学生面对一些“动态型”的应用问题常常会束手无策.如果能想象问题的动态情景,寻找临界条件,问题就能迎刃而解.比如本文中研究的这道题,求蚂蚁从点A爬行到点B的最短路径,就是一个动态问题.最终把其转化为:当点A,E,B在一条直线上时最短,此时点E的位置就是一个临界点.在教学的过程中,鼓励学生由一些特殊的情况进行大胆的猜想,再尝试用严格的数学方法进而论证一般情况,培养学生特殊与一般的数学思想,进而培养学生敢于质疑,勇于创新的科学品质.
(五)在日常教学与解题教学中,注重分析的过程,有大局观
平时解题过程中,学生倾向于想到一步,就求解一步,以“量”的形式解题,缺乏对题目的定性认识:这可求吗?为什么可求?要想提高学生的定性认识,我们在平时的教学中要有意识地去让学生定性的分析求解的过程,有哪些条件可求什么,进而可求什么,这样的分析方式;在代数教学时渗透各个公式中有几个未知量,知道其中几个量其余几个量就可求的思想;在几何教学中渗透“确定即可求”的思想:如三角形的两边及其夹角确定,三角形也随之确定,进而三角形的其他基本元素也是确定的,可求解的等等.

