巧用圆规解决折叠问题——以一道中考题的分析为例

广东省广州市增城区石滩中学(511330) 陈明双

折叠:指把物体的一部分翻转和另一部分贴拢.“折叠问题”在初中数学主要应用于轴对称变换这类几何题型.

近几年来,“折叠问题”在全国各地数学题中频繁出现,而更多时候是在中考的压轴题当中出现该类问题,它通常与动点型的问题相结合,所涉及的考点主要有图形的性质、轴对称的性质和勾股定理的应用,主要考查学生的几何直观,空间观念,推理能力,转化思想、方程思想、分类讨论思想等等.对于此类问题,它对学生的读题能力、识图能力、作图能力有更高的要求.“折叠问题”大多数呈现于动点问题当中,而学生一遇到动点问题就束手无策.

1 试题呈现

在矩形ABCD中,BC=3,动点P从B出发,以每秒1 个单位的速度,沿射线BC方向移动,作ΔPAB关于直线PA的对称ΔPAB′,设点的运动时间为t(s).

(1)若AB=

①如图2,当点B′落在AC上时,显然ΔPAB′是直角三角形,求此时的t值;

②是否存在异于图2的时刻,使得ΔPCB′是直角三角形? 若存在,请求出所有符合题意t的值;若不存在,请说明理由;

图1

图2

(2)当点P不与点C重合时,若直线PB′与直线CD相交于点M.且当t <3 时存在某一时刻有结论成立,试探究:对于的任意时刻,结论∠PAM=45°是否总是成立? 请说明理由.

分析本题的条件以作三角形关于某直线成对称图形为背景,实际上就是一道有动点问题的折叠题目.它考查了图形的相似、勾股定理、轴对称的性质等知识点,涉及的数学思想有方程思想、转换思想、分类讨论思想.

2 题目分析及解答

2.1 题目分析

这是一道典型的“折叠”题目,题目以第(1)小题第①问为第一个台阶,提示学生该道题的折痕为直线AP,而本题的困难点就在于P点是运动的,从而导致折痕是一条变化的直线,也就是说:点B的对称点B′落在何处是不确定的.第(1)小题第②问常规的作答方法是抓住ΔPCB′是直角三角形这个条件,在ΔPCB′的三个内角当中,哪一个内角是直角将作为本题分类讨论的标准.

2.2 题目解答

(1)①解法一:由对称的性质得到两个三角形全等,再用勾股定理得出三角形三边的关系,采用方程的思想得出一条关于t的方程,从而求出t=

解法二:利用相似三角形的对应边成比例也可得到一条关于t的方程,从而求出t的值.

②∵ΔPAB与ΔPAB′关于直线PA对称,∴ΔPAB∠PB′C=90°,在矩形ABCD中,∴∠D=90°,AB=

如图2-1,当∠PCB=90°时,∴CB′=CD−DB′=∴PC=3−t,在RtΔPCB′中,由勾股定理得

图2-1

如图2-2,当∠PCB′=90°时,∴CB′=CD+DB′=∴PC=t−3,在RtΔPCB中,由勾股定理得B′P2=PC2+B′C2,∴t2=+(t−3)2,∴t=6.

图2-2

如图2-3,当∠CPB′=90°时,∵∠DAB=∠B=CPB′=90°,∴四边形ABPB′为矩形,∴AB=AB′=∴矩形ABPB′为正方形,∴t=BP=

图2-3

(2)解略.

3 题目解答反思

本题的(1)②是该题目的精髓部分,它既是一个动点问题,又是一个折叠问题.《义务教育数学课程标准(2011年版)》在评价建议中提出:“在对学生进行评价时,教师可以关注以下几个不同的层次:第一,学生是否能理解题目的意思,能否提出解决问题的策略,如通过画图进行尝试……”题目当中,点P的运动路径是一条射线,也就是说折痕AP不确定,这样一来,要画出该题的图形的难度就加大了.但是,题目当中的“ΔPCB′是直角三角形”这个条件给学生解答改题目指引了方向,一般地,学生和教师看到该条件时都会采用分类讨论的方法对三角形的三个内角进行分类:(1)当∠PCB′=90°时;(2)当∠CPB′=90°时;(3)当∠PB′C=90°.而第(3)种情形很明显就不存在.所以,学生就会针对第(1)(2)这两种情况进行画图解答.所以,在大部分学生画的图形当中,他们认为∠PCB′=90°这种情形已经画出来了(如图2-1),因此漏掉了图2-2 这种情况,导致t的结果只有两种.

4 技巧呈现

《义务教育数学课程标准(2011年版)》在课程设计思路中指出:“几何直观主要是指利用图形描述和分析问题,借助几何直观,可以把复杂的数学问题变得简明形象,有助于探索解决问题的思路,预测结果.几何直观,可以帮助学生直观地理解数学,在整个数学学习过程中都发挥着重要作用.”

通过以上的分析,我们借助几何直观,找出“折叠问题”中不变的量,另辟蹊径,动中找定,从另一个角度来分析改题目当中的几种情形,做到不偏不漏.

在日常的数学学习当中,我们通常会借助数学工具——三角尺、圆规作图,而利用圆规作图时,它作出来的图形不仅仅是一个圆形,圆里面隐含着很多不变的量：半径、直径、直径所对的圆周角等等.

在解答改题目时,最关键的是做出ΔPAB的对称图形ΔPAB′,因此,我们先不去考虑题目当中“ΔPCB′是直角三角形”这个条件,先考虑动点的运动轨迹,我们已经知道点P的运动路径是一条射线,那么点B′的运动轨迹呢?由轴对称的性质可知,在点B′的运动过程中,它总是保证AB′=AB这个不变的量,所以我们可以以A为圆心,线段AB的长为半径作圆(如图3).这样一来,点B′的运动轨迹就是⊙A,我们就可以很轻松的画出ΔPCB′的几种情形.

图3

5 方法应用

例1如图4,在矩形纸片ABCD中,AB=4,AD=6,点E是AB的中点,点F是边AD上的一个动点,将ΔAEF沿EF所在直线翻折,得到ΔA′EF,求线段A′C的最小值.

图4

分析本题是一道折叠的动点问题,题目中的点E是定点,点F是主动点,点A′是从动点,在点的运动过程中,一直遵循EA′=EA这个条件,因此,我们可以引导学生使用圆规以为圆心,EB为半径作圆,由此看到点A′的运动轨迹,所以,当E,A′,C三点共线时,从而得到A′C的最小值为

图4-1

例2如图5,在边长为4 的正方形ABCD中,E,F分别是边BC、DC上的动点,且EF=4,Q为EF中点,P是边AD上的一个动点,求PQ+PB的最小值.

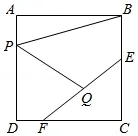
图5

图5-1

分析本题是一道典型的动点最值问题,E,F是主动点,Q为EF中点这个条件可以发现CQ的长度是一个定值,所以,点Q的运动轨迹是以为圆心,2 为半径的圆弧上,由此我们可以引导学生借助圆规找到点Q的运动轨迹,题目要求PQ+PB的最小值,而点P也是动点,B、Q在定直线AD的同一侧,我们可以借助折叠,做B点关直线AD的对称点B′,这样可以得到PB=PB′,所以,当B′,P,Q三点共线时,PQ+PB′最小,即PQ+PB最小.

6 感悟

图形的运动来源于我们的生活,几何变换实质就是图形的运动,我们在解决含有动点的“折叠问题”时,要善于在动中求静,找出题目当中不变的元素,采用几何直观帮助学生直观的理解数学,运用数学.