GeoGebra在高中数学教学中的应用举例
江苏省扬州市扬州大学数学科学学院(225000) 刘 杰
1 GeoGebra 介绍
GeoGebra 是由美国佛罗里达州亚特兰大学的Markus Hohenwarter 教授在2002年设计的,是一款将几何、代数、表格、图形、统计和微积分整合在一起的动态的教学软件,对于传统的动态教学软件如几何画板来说,它不仅可以构造各种几何图形、函数图像,而且可以比较条理清晰地看到作图的代数过程步骤,“数”与“形”同步显现,十分方便.如图1软件分为代数区和几何区,代数区负责列出对象的数学式形态的定义,几何区负责显示对象如点、线、图形、轨迹等.
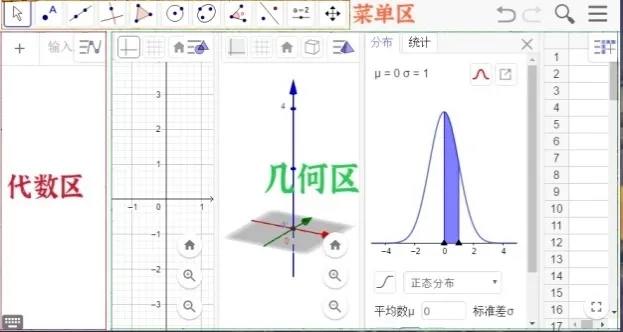
图1
2 GeoGebra 在教学中应用举例
2.1 初等函数中教学应用——以指数函数为例
函数在高中数学知识的学习中是重点和难点,主要学习其概念以及图像与性质,而对于函数的性质都是从图像中总结而来,所以在教学中更多的是让学生从图像进行自主总结归纳,仅靠“描点法”等传统方法作图,只能展现函数的局部特征,一些关键点无法直观的看到坐标,影响学生的探究过程,就有必要借助现代信息技术来完成.
指数函数图像探究过程主要让学生考虑指数函数概念中底数有限制范围的原因,让学生画出一些特殊函数图像,引发思考做出假设,然后进行归纳总结指数函数性质.教师所要做的是利用GeoGebra 整合学生画出的图像让他们易于观察做出假设,并最后利用GeoGebra 展示图像因为底数a的变化而动态变化的过程,见图2,总结指数函数的图像及其相关性质,而且软件中所做出的不同函数图像是自带不同颜色、标签的,方便对其进行隐藏或显示操作,图像不易混淆,非常方便教学操作也有益于学生观察.
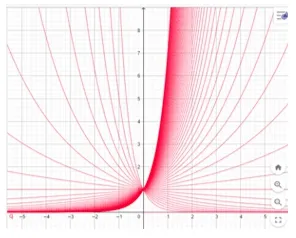
图2
2.2 立体几何中教学应用——以旋转体为例
立体几何的学习中,学生不仅要有逻辑思维能力还需要空间想象能力,是落实数学核心素养的重要内容,通过学习培养学生的空间直观感知能力,能够有逻辑的去判断空间中各个元素的位置关系.高考中的立体几何学生大部分选择用向量法解题;在传统的教学中一些简单的立体几何图形教师一般是动手做简易模型让学生观察线面位置等,但是对于复杂的立体几何则无法展现,教师则需要充分利用多媒体更加直观而且精准的向学生展示三维图形的各个面,或者从二维图形向三维图形转化的过程,让学生理解立体几何的本质,建立空间观念.
基本立体图形是学习其他立体几何的基础,学生需要了解立体几何的分类以及形成过程,能对复杂立体几何的构成元素进行分析.利用GeoGebra 让学生直观看到从二维图形到三维立体几何的动态过程,了解知识本质,激发学习兴趣,见图3圆锥的形成,实现由二维三角形旋转得到圆锥立体.
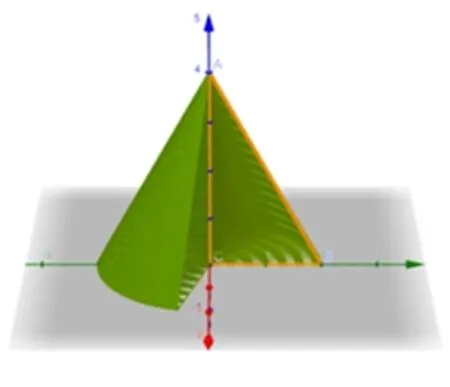
图3
2.3 圆锥曲线中教学应用——以圆锥曲线定义为例
圆锥曲线在实际生活中都有很多应用,如火力发电厂的冷却塔运用到了双曲线模型,行星的运动是椭圆模型,自由落体、拱桥等涉及抛物线的知识.圆锥曲线在高中知识中是一个重点及难点问题,因为其中涉及的知识点比较多包括抛物线、椭圆、双曲线的定义和各种性质,出题方面变化多端,不仅与直线、三角形、圆等知识进行融合而且还需要比较强的逻辑运算能力,出题类型多有求轨迹方程、定点定值、定比、最值范围等,对学生的能力要求比较高.学生在做题中难以下手主要还是对于圆锥曲线的性质等问题理解的不够透彻,不能应对多变的提问方式,所以就要求教师在教学中应该注重对于直观想象力进行培养,将圆锥曲线进行直观、形象地展示,以促使“数”与“形”能够有效融合.
椭圆、双曲线、抛物线为何叫圆锥曲线,这就要追究到圆锥曲线的形成过程,此为知识的发生、发展过程,需要教师向学生展示知识本质,也是数学文化的渗透过程.教师可以利用GeoGebra 直观演示平面斜截圆柱所得的交线的种类,见图4,以此来引入圆锥曲线知识.其中教师可以用丹德林双球模型推导出椭圆的焦半径性质,见图5,既有助于学生对椭圆定义的理解,也让学生了解数学曲折的发展过程,提高学生学习兴趣.
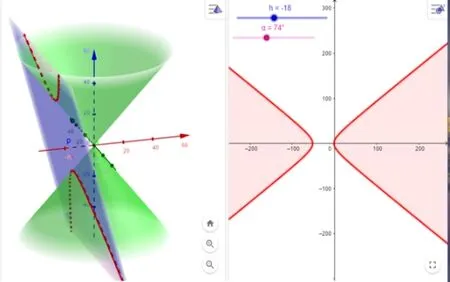
图4
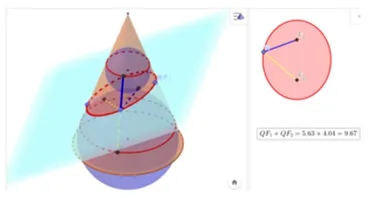
图5
2.4 概率与统计中教学应用——以正态分布为例
概率与统计内容在日常生活中或多或少都有涉及,在教学过程中这部分内容的教学与案例也都是与生活情境密切相关的,让学生深切了解生活中有数学,数学与生活密切相关,在信息技术发展的今天,对学生也提出了相应的技能学习,课程标准中的数据分析的核心素养也体现了这一点.通过学习这部分的内容,提高学生对随机性的认识,并能够初步学会收集数据,整理数据,分析数据,传统教学中教师会利用课本上的案例来进行知识讲解,直接根据所给数据得出统计图表,学生没有经历收集、整理、分析数据的过程,只是机械的学会如何从图表中求频率,教学最重要的是要让学生经历统计的过程,为了增加课堂效率和质量,避免手动画图带来的误差,利用信息技术直观展现作图,为学生提供了有理有据的图表,提升了课堂的趣味性和教学效果,也有助于对于数据的分析.
正态分布是连续型随机变量的一种分布形式,在统计中可以说是经常见到,在进行教学时,需要讨论参数µ和σ对正态分布曲线的影响,以及一般正态变量落入任意区间的概率,教师通过GeoGebra 可以任意改变参数µ和σ,让学生看到曲线随参数变化的规律,也可直接通过“概率统计”几何区改变,见图6.
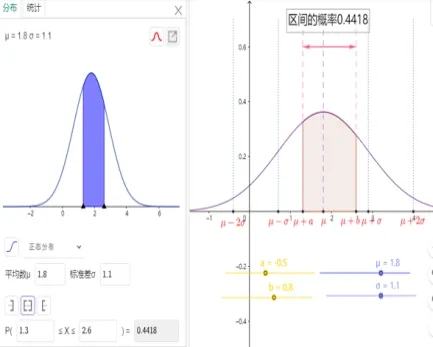
图6
3 利用GeoGebra 进行教学的几点思考
3.1 教师要熟练操作信息技术,提高课堂效率
教师要紧跟时代发展,学习有利于课堂有利于学生发展的教学技能,现代课堂由以板书为主转化成以多媒体展示为主,教师不仅要了解而且要熟练运用多媒体软件,在课前做好准备,也要在课上能现场操作例如转变相关参数、直接展现操作步骤让学生直观理解知识,有效率地学到知识.
3.2 教师要合理利用信息技术,提高课堂质量
教师要深入研究教材和教学内容,寻找教学与信息技术融合的最佳内容和最佳方式,不能说为了用信息技术而用信息技术,要使信息技术用的有用、有效,能够让学生比不用信息技术更能理解知识的本质.教师操作的时候让学生专注于知识本身,而不是去追求图形绚丽多彩的表面变化场景,这就需要教师做课件去思考相关情况并在课上通过语言去引导学生,提高课堂质量.
3.3 教师要深入发掘信息技术,展现数学价值
教师在教学中融入信息技术并不只限于教材中的知识点,数学是科学的、实用的、文化的、思想的,具有多方面价值,教师要深入挖掘数学知识中存在的价值,并将其生动地展现给学生,由此教师可以借助信息技术,让学生感受数学的价值存在,如通过绚丽多彩的勾股树展示数学定理,用形态多样万花尺来体现数学的美学价值,培养学生的理性思维,激发学生寻求数学发展历史,提高数学的文化素养和创新意识.
4 结语
《普通高中数学课程标准(2017年版2020年修订)》(以下简称《课程标准》)中明确指出“注重信息技术与数学课程的深度融合,提高教学的实效性”.信息技术融入课堂已经不是一个新的话题,但是大多还只是PPT 的展示,有时候并没提高课堂教学的质量,如何在课堂中有效融入信息技术是一个重要问题,教师借助GeoGebra 等教学软件,寻求与教学结合的最佳方式,向学生直观、动态地展现数学知识的生成、演变过程,有利于学生了解知识本质,更能让数学知识不再枯燥无味,让课堂气氛变的活跃,增进师生交流,提升数学素养.

