2019版新教材中数学建模的模型探究及其在教学中的作用*
广东省广州市铁一中学(510600) 范选文
1 数学建模的内涵
从定义的层面上来说,所谓数学建模就是分析和研究一个实际问题时,从定量的角度出发,基于深入调查研究、了解对象信息、作出简化假设、分析内在规律等工作的基础上,用数学符号和语言,把实际问题表述为数学式子,即数学模型,然后用通过计算得到的模型结果来解释实际问题,并接受实际的检验,这个建立数学模型的全过程就称为数学建模.
数学建模是数学学习的一种新的方式,它为学生提供了自主学习的空间,有助于学生体验数学在解决实际问题中的价值和作用,体验数学与日常生活和其他学科的联系,体验综合运用知识和方法解决实际问题的过程,增强应用意识;有助于激发学生学习数学的兴趣,发展学生的创新意识和实践能力.
2 高中教材中的数学模型
根据徐利治先生在《数学方法论选讲》一书中所谈到,所谓“数学模型”(Mathematic Model)是一个含义很广的概念,粗略的讲,数学模型是指参照某种事物系统的特征或数量相依关系,采用形式化数学语言,概括地或近似地表达出来的一个数学结构.广义的说,一切数学概念、数学理论体系、数学公式、数学方程以及由之构成的算法系统都可以称为数学模型;狭义的解释,只有那些反应特定问题或特定的具体事物系统的数学关系结构才叫数学模型.
高中数学教材的是数学模型有:函数模型,三角模型,数列模型,几何模型,概率模型和统计模型等,在2019 版的新教材中编写了两个数学建模活动,必修第一册的建立函数模型解决实际问题与选择性必修第三册的建立统计模型进行预测.
2.1 建立函数模型解决实际问题
用函数的观点解决实际问题是中学数学中最重要的、最常用的方法.用函数构建数学模型解决实际问题时,首先要对实际问题中的变化过程进行分析,析出其中的常量、变量及其相互关系;明确其运动变化的基本特征,从而确定它的运动变化类型.然后根据分析结果,选择适当的函数类型构建数学模型,将实际问题化归为数学问题;再通过运算、推理,求解函数模型.最后利用函数模型的解说明实际问题的变化规律,达到解决问题的目的.
建立函数模型活动的过程:(1)观察实际情景,发现和提出问题;(2)收集数据;(3)分析数据;(4)建立模型;(5)检验模型;(6)求解问题.
高中数学函数模型有:一次函数模型,二次函数模型,反比例函数模型,指数函数模型,对数函数模型,幂函数模型和三角函数模型.
2.2 建立统计模型进行预测
在现实世界中有许多随机现象需要研究.已有的学习告诉我们,研究随机现象,就是要在明确研究对象和问题的基础上,通过收集数据、整理数据、提取信息、构建数学模型,再利用模型进行推断,得出结论.通过这样的研究所得出的结论,可以为我们作出决策提供有力的依据.
建立统计模型活动的过程:(1)了解背景知识,明确分析目的,确定获得数据方法;(2)观测数据(收集样本数据);(3)统计描述;(4)统计模型;(5)统计推断;(6)得出结论和做出决策.
高中数学统计模型有:一元线性回归模型,非线性回归模型和独立性检验模型.
下面看一个建立函数模型解决实际问题的实例
(1)观察实际情景,发现和提出问题
中国茶文化博大精深,茶水的口感与茶叶类型和水的温度有关.经验表明,某种绿茶用85°C 的水泡制,再等到茶水温度降至60°C 时饮用,可以产生最佳口感.那么在25°C 室温下,刚好泡好的茶水大约需要放置多长时间才能达到最佳饮用口感?
(2)收集数据
某研究人员每隔1min 测量一次茶水温度,得到下表(表1)的一组数据.

时间/min 0 1 2 3 4 5水温/°C 8500 79.19 74.75 79.19 68.19 65.10
(3)分析数据
根据所收集的数据,利用Excle 画出散点图,如上图所示.
(4)建立模型
根据散点图的趋势可以拟合为线性的一次函数模型,也可以拟合为指数函数的模型,下面我们利用Excle 的拟合功能,直接可以求解出两个函数模型的表达式.
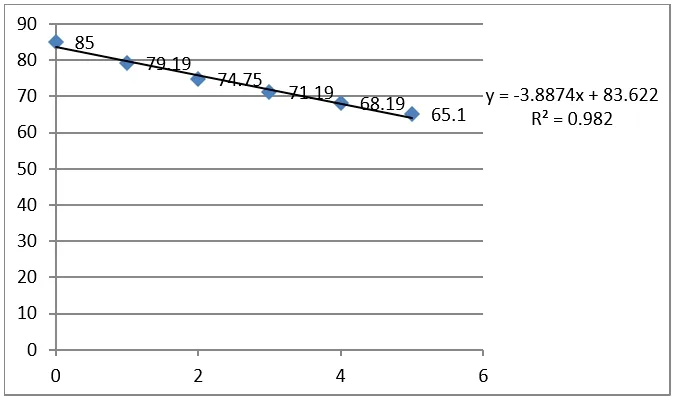
拟合为一次函数模型(模型1) 的表达式为:y=−3.8874x+83.622,R21=0.982.
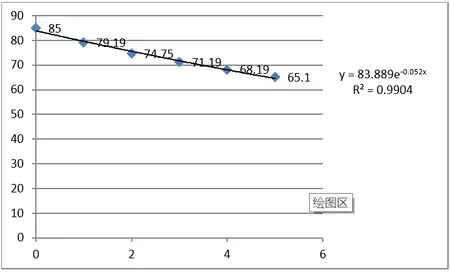
拟合为指数函数模型(模型2) 的表达式为:y=83.889e(−0.052x),R22=0.991.
(5)模型检验
模型1 检验:当x=5 时,y1=64.185;
模型2 检验:当x=5 时,y2=64.683;
因为|y2−65| <|y1−65| <0.5,且R22>R21>0.95,所以可以判断出用两个函数模型都能很好的反映茶水温度随时间变化的规律,相比之下利用指数函数模型进行拟合会更优.
(6)求解问题
我们利用指数函数模型(模型2)进行求解,当y=60时,解得x ≈6.445.所以,泡制一杯最佳口感茶水所需时间大约是7min.
3 数学建模在高中数学教学中的作用
3.1 数学建模能提高学生的主体意识
在课堂教学中真正落实学生的主体地位,让学生真正成为数学课堂的主人,促进学生自主地发展,是现代数学课堂的重要标志,是高中数学素质教育的核心思想,也是全面实施素质教育的关键.高中数学建模活动旨在培养学生的探究能力和独立解决问题的能力,学生是建模的主体,学生在进行建模活动过程中表现出的主体性表现为自主完成建模任务和在建模活动中的互相协作性.中学生具有好奇、好问、好动、好胜、好玩的心理特点,思维开始从经验型走向理论型,出现了思维的独立性和批判性,表现为喜欢独立思考、寻根究底和质疑争辩.因此,教师在课堂上应该让学生充分进行自主体验,在数学建模的实践中运用这些数学知识,感受和体验数学的应用价值.教师可作适当的点拨指导,但要重视学生的参与过程和主体意识,不能越俎代庖,目的是提高学生进行探究性学习的能力、提高学生学习数学的兴趣.
3.2 数学建模能培养学生的能力
数学建模教学体现了多方面能力的培养:
(1)翻译能力.能将实际问题用数学语言表达出来,建立数学模型,并能把数学题的解用一般人所能理解的非数学语言表达出来;
(2)运用数学的能力.表现在能用数学工具对所建立的数学模型进行处理;
(3)交流合作能力.数学建模活动中常常是小组分工合作、密切配合、相互交流、集思广益,这种互相合作的精神是社会生活中极为需要的;
(4)创造能力.数学建模没有现成的答案,也没有现成的模式或通式,建模的过程有较大的灵活性,建模的结果一般说来只有最优解答,而非标准解答.这样,有助于培养学生的想象力和洞察力.
3.3 数学建模能促进课堂教学
(1)积极创设数学问题情境,激发学生建模热情
结合学生的认知特点和对数学知识的掌握情况,从学生的实际出发适当选编问题作为学生建模的基础,并为学生在建模过程中提供必要的指导和充分的交流,以激发学生的建模热情.
(2)概括问题,从问题中抽象出数学化模型
建模的过程就是对实际问题进行概括抽象的过程,通过对问题的交流、探讨与整理,抽象出数学化的式子或方程.在数学化的过程中,教师应作出及时调控,以便于学生从观察、猜测中形成正确的思路与方法.
(3)对数学模型进行探究分析,形成数学素养
数学模型的建立过程,需要通过启发和指导,使学生获得对数学知识、思想和方法的真实体验,并从课题的分析和总结中受到数学素养的熏陶.
(4)利用数学知识解决实际问题,享受成功的喜悦
问题的解决总是伴随着成功的体验,数学模型的建立为实际问题的解答打开了智慧的大门,学生在运用知识的过程中体验到了方法的重要和思想的威力.
在2019 版新教材中,数学建模应用于很多章节,例如如应用于数学概念、定义和定理的教学之中,应用于解决数学问题的教学之中等等.数学建模是应用数学解决实际问题的基本手段,也是推动数学发展的动力.数学建模作为“六大核心素养”之一,在数学建模核心素养的形成过程中,积累用数学解决实际问题的经验.学生能够在实际情境中发现和提出问题;能够针对问题建立数学模型;能够运用数学知识求解模型,并尝试基于现实背景验证模型和完善模型;能够提升应用能力,增强创新意识.所以数学建模在高中数学中具有广阔的发展前景和重要的应用.

