钢纤维增强水泥基复合材料增韧机理研究

曲博扬，卿龙邦

(河北工业大学土木与交通学院，天津 300401)

0 引 言

混凝土是目前土木水利行业中使用量最大的建筑材料，但其存在内部有初始缺陷、抗拉强度低、韧性差等问题[1]，在荷载作用下容易产生开裂、破坏。在混凝土材料中掺入纤维[2-7]，在一定程度上改善了混凝土受力性能，增强混凝土的抗拉强度、抗裂性能和耐久性，抑制混凝土内部裂缝的开展，延缓混凝土宏观裂缝的形成，提高了材料的适用性。研究表明纤维方向对混凝土力学性能影响很大[8]，通过特殊的定向装置，可以使纤维按一定规律排列，可显著提高特定方向混凝土强度、韧度[9]。定向钢纤维水泥基复合材料具有高强度、高韧性、高耐久性等特点，适用于桥梁、道路、隧道、港口、能源等对结构抗裂性要求高的工程，在我国已广泛应用于桥隧及物流工程中。

由于结构中受力复杂，混凝土的开裂通常是复合型断裂形态，其中又以同时受拉应力与剪应力的Ⅰ-Ⅱ复合型断裂为主，它的开裂方向与所受两种应力比例有关。为研究混凝土在复杂受力情况下断裂的临界条件，许多学者通过理论计算与试验拟合得到了不同的Ⅰ-Ⅱ复合型断裂临界判断依据。Erdogan等[10]提出了最大周向应力准则，从裂缝尖端最大应力的角度解释了裂缝扩展临界状态。最大周向应力准则是根据应力强度因子判断断裂性能的方法之一，其形式较为简单，计算略复杂，是应用最广泛且可靠的计算方法。邓宗才等[11]提出的最大拉应变准则，从裂缝尖端附近最大环向拉应变判断临界状态，相比于最大周向应力准则，安全系数更高。Hussain[12]提出的最大能量释放率判据，从裂缝产生最大能量释放率的角度分析了Ⅰ-Ⅱ复合型裂缝的断裂准则，由于复合型裂纹扩展时不再沿着裂纹本身原有方向，而是存在一定的开裂角度，原来能量释放率的公式不再适用，而具有开裂角的复合型裂纹能量释放率的公式比较复杂且目前方法没得到统一。Sih[13]基于应变能密度场断裂，推导出最小应变能密度因子判据，通过比较裂缝尖端局部应变能密度来判断临界状态，理论上能够适用于所有复合型裂缝的扩展问题。许斌等[14]在考虑裂纹尖端混凝土双向受力的情况，提出了改进最大周向应力准则。刘梦和等[15]在三点弯曲梁和四点弯曲梁试验的基础上，对复合型裂缝的混凝土断裂能进行了理论分析和数值模拟，建立了完整的断裂能G判据。于骁中等[16]通过进行四点弯曲梁试验，推导了用于评价混凝土Ⅰ-Ⅱ复合型断裂的经验公式。徐世烺等[17]通过对不同缝高比的四点剪切梁试验，提出了不同于极限荷载确定的起裂准则，并研究了缝高比对起裂准则的影响规律。

Eshebly等效夹杂理论是解决复合材料微观力学问题中常见的方法之一，将其应用于最大周向应力准则中，可以更全面的解释影响钢纤维增强水泥基复合材料断裂性能的因素。本文通过研究裂缝尖端应力场在钢纤维作用下的变化，结合Eshebly等效夹杂理论和最大周向应力准则，推导了复合应力作用下无限大薄板中，钢纤维方向对裂缝尖端应力强度因子(SIF)的影响与最大应力表达式，建立了钢纤维影响下的裂缝尖端应力计算方法。通过不同钢纤维方向下裂缝尖端的最大应力比，解释了钢纤维角度、相对位置和纤维材料参数对水泥基复合材料Ⅰ-Ⅱ复合型断裂性能的提高作用。

1 理论模型

图1(a)为无限大平面薄板上有一长度为2a的中心贯穿裂缝，无限远处同时作用双向均匀拉应力σ与剪应力τ，裂缝尖端附近有一长度为2L，直径为b的钢纤维。钢纤维与裂缝尖端相对位置如图1(b)所示，β为钢纤维与竖向方向的夹角，r0为裂缝尖端到钢纤维水平投影距离的最小值，θ1、θ2分别为裂缝尖端到钢纤维上、下边缘与x轴正向的夹角。

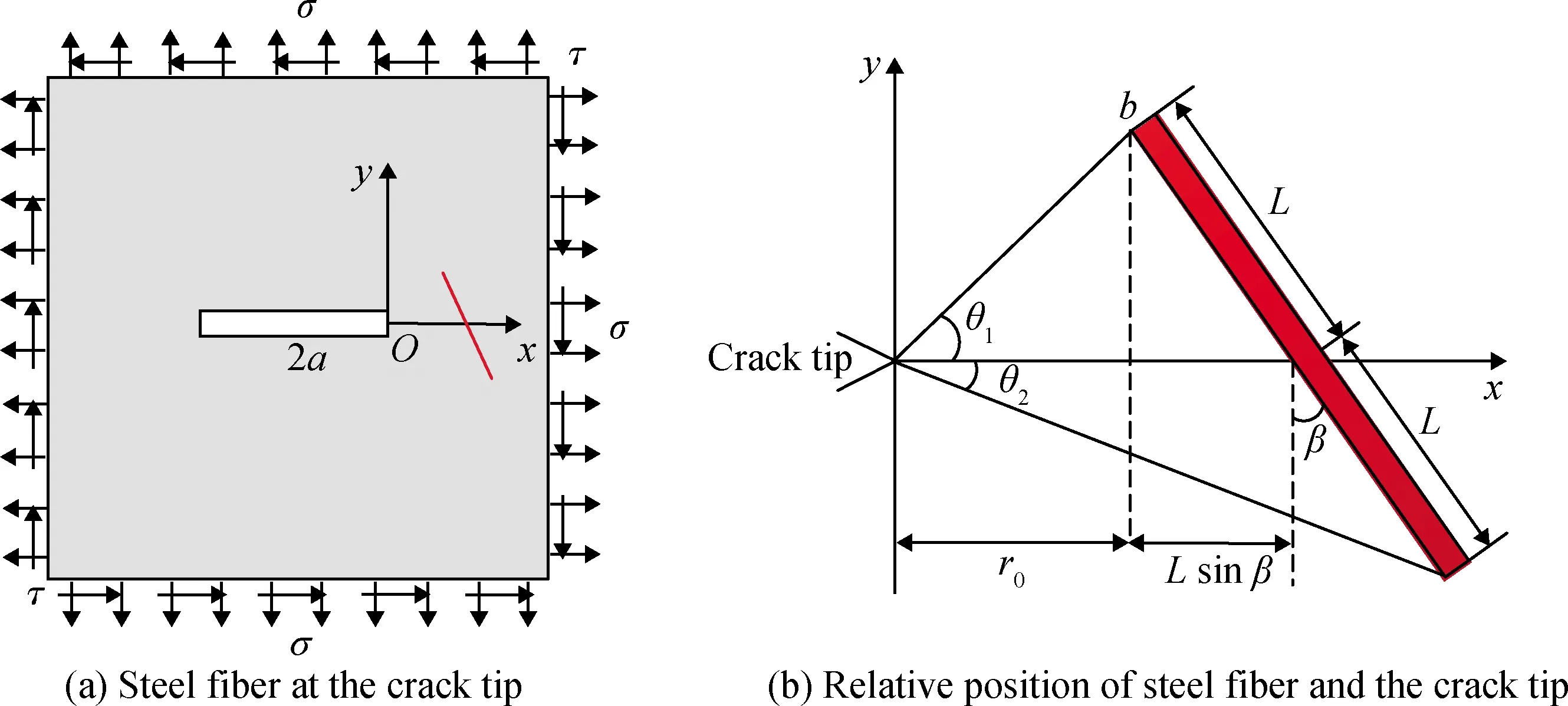
图1 无限大平面板中双向拉伸均匀受剪作用下的Ⅰ-Ⅱ复合型断裂Fig.1 Ⅰ-Ⅱ combined fracture under biaxial tension and uniform shear in infinite plane

2 数值计算

2.1 等效夹杂原理

根据Eshebly等效夹杂理论[18]，当裂缝尖端附近存在钢纤维时，会改变复合型裂缝尖端应变场。设在直角坐标系中，无钢纤维影响下裂缝尖端附近应力场σ为：

σ=(σ11σ22τ12)T

(1)

根据广义胡克定律，裂缝尖端应变场e可表示为：

(2)

经过钢纤维影响后的等效转换应变场et为：

et=[(Ci-Cm)S+Cm]-1(Cm-Ci)e

(3)

式中：σ为裂缝尖端一点的应力场；σ11、σ22分别为沿x轴、y轴的拉应力分量；τ12为此点所受的剪应力；e为裂缝尖端同一点的应变场；e11、e22分别为沿x轴、y轴的拉应变分量；e12为此点的剪应变；et为经过钢纤维影响后的裂缝尖端等效转换应变场；Em为水泥基体弹性模量；v0为平面应变问题中的水泥基体泊松比；Ci为夹杂物弹性张量；Cm为水泥基体弹性张量；S为二阶Eshebly张量，其表达式为：

(4)

对于长纤维域，其分量可表示为：

(5)

(6)

(7)

(8)

通过计算得到夹杂影响后的应变场：

(9)

2.2 应力强度因子

根据文献[19]，由式(9)可以得到在平面应变条件下，由应变场变换引起的裂纹尖端应力强度因子的变化。将平面应变转换为平面应力问题可以分别得到Ⅰ、Ⅱ型裂缝在任意方向钢纤维作用下的应力强度因子解[20-21]。

(10)

(11)

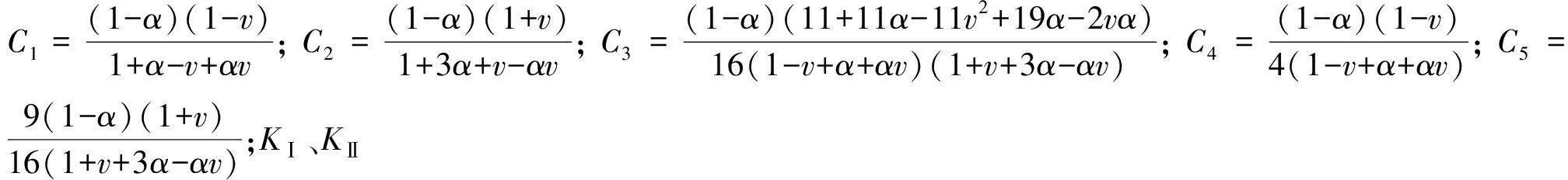
当钢纤维与裂缝尖端位置如图1(b)所示时，分别对式(10)、(11)积分，可以得被钢纤维影响后裂缝尖端应力强度因子分别为：

(12)

(13)

式中：KⅠ-tip、KⅡ-tip分别为钢纤维影响后的Ⅰ、Ⅱ型断裂裂缝尖端应力强度因子。

2.3 开裂角和最大周向应力

当复合型裂缝扩展时，裂缝扩展的方向是周向应力σφ取最大值的方向，当周向应力的最大值达到裂缝扩展应力临界值时，裂缝开始失稳扩展。根据叠加原理，平面应力条件下无限大平面裂缝尖端附近一点(r,φ)的应力场的极坐标形式可用式(14)～式(16)表示。

(14)

(15)

(16)

式中：(r,φ)为极点定义在裂缝尖端时一点的极坐标；σr为平面内一点所受的法向应力；σφ为平面内同一点所受的周向应力；τrφ为平面内同一点所受的剪应力。

通过对式(15)中φ求偏导数，使σφ取得极值，计算得裂缝开展方向φ0和此方向上的最大周向应力为：

σsinφ0+τ(3 cosφ0-1)=0

(17)

(18)

式中：φ0为裂缝开展方向与裂缝方向的夹角；σφ0 max为φ0方向上的最大周向应力。

3 参数影响

3.1 钢纤维角度对增韧效果的影响

将式(12)、(13)分别代入式(17)、(18)可得到掺入纤维后裂缝开裂角φβ和影响后最大周向应力σφβ。令模型所受应力组合p=σ/τ，可以化简得σφβ/σφ0 max=f(p)，即在钢纤维自身物理性质，裂缝与钢纤维位置相同时，σφβ/σφ0 max只与应力组合p有关。为分析不同应力组合p，不同纤维方向β，不同距离r0对开裂角度和掺入纤维前后最大应力之比的关系。本文取水泥基体弹性模量Em=30 GPa，钢纤维弹性模量Ei=210 GPa，泊松比v=0.2，裂缝半长度a=10 mm。

通过计算得到在不同钢纤维方向下，应力组合与开裂角差值Δφ=φ0-φβ之间的关系如图2所示。φ0为不掺入钢纤维时裂缝的开裂方向，φβ为钢纤维与竖直方向的夹角为β时裂缝的开裂方向。从图2可以看出，钢纤维方向对开裂角的影响较小。随着应力组合p的增大，开裂角度差值Δφ呈现先增大后不断减小的整体趋势，复合型断裂逐渐由剪应力控制的Ⅱ型断裂向由正应力控制的Ⅰ型断裂转变，开裂方向不断靠近裂缝延伸方向。相同应力比值对开裂角度差值的影响，钢纤维定向(0°)时比乱向更显著。

在不同应力组合p下，通过改变钢纤维方向，可以得到钢纤维-竖直方向夹角β与裂缝尖端应力的关系。图3显示了在p一定的情况下，不同方向钢纤维与裂缝尖端最大应力比的关系。增韧效果在纤维-竖直方向夹角为0°～20°时快速减弱，20°～75°时变化逐渐平缓，75°～90°时能力增强，但效果仍低于钢纤维与裂缝方向垂直时。随着应力比值p的增大，断裂模式不断向Ⅰ型断裂模式靠近，增韧效果略有降低。在应力组合p取0～5的情况下，随机乱向钢纤维裂缝尖端最大应力比的期望值在0.980 8～0.987 5，而定向钢纤维(β=0°)裂缝尖端最大应力比值为0.910 3～0.942 5，钢纤维定向后可以使Ⅰ-Ⅱ复合型裂缝尖端最大应力取最小值，从而减少裂缝的开展。

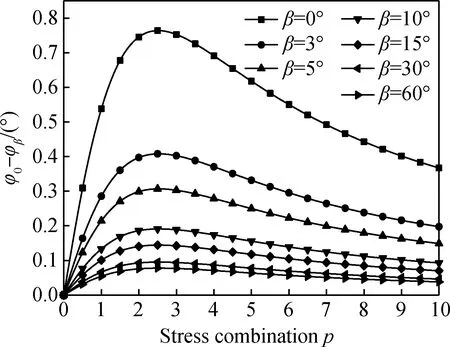
图2 应力组合-开裂角度关系图(r0=0.5 mm)Fig.2 Relationship between stress combination and cracking angle (r0=0.5 mm)

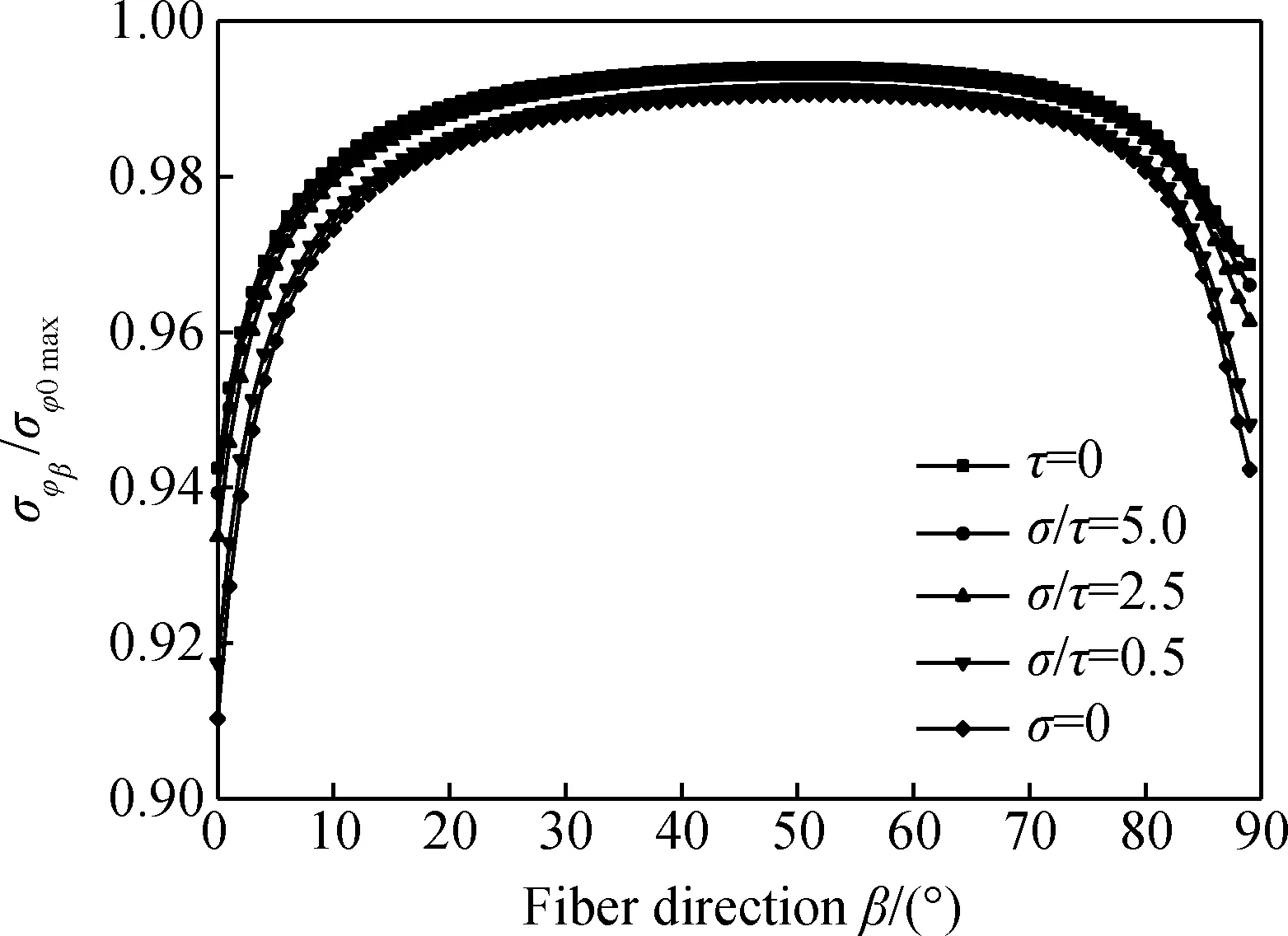
图3 纤维方向β-σφβ/σφ0 max关系图(r0=0.5 mm)Fig.3 Relationship of fiber direction and σφβ/σφ0 max (r0=0.5 mm)

3.2 钢纤维位置和弹性模量对增韧效果的影响

当钢纤维-竖直方向夹角β一定时，通过改变裂缝尖端与纤维水平投影距离最小值r0可以得到应力组合与σφβ/σφ0 max的关系如图4所示。在钢纤维-竖直方向夹角β相同时，裂缝尖端与钢纤维水平投影的距离r0越大，纤维对裂缝尖端应力影响越小，增韧效果随距离增大而快速减弱。

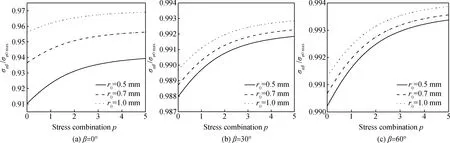
图4 应力组合-σφβ/σφ0max关系Fig.4 Relationship between stress combination and σφβ/σφ0 max

表1 不同弹性模量、不同钢纤维方向下的ξn(r0=0.5 mm,σ/τ=3)Table 1 ξn under different elastic modulus and steel fiber direction (r0=0.5 mm, σ/τ=3)

表2为裂缝尖端应力减值降低幅度与钢纤维方向的关系，随着钢纤维弹性模量的增大，相同角度下裂缝尖端应力下降的幅度降低。钢纤维弹性模量对于定向钢纤维(钢纤维与裂缝方向垂直)的影响大于对随机分布钢纤维的影响。

表2 不同钢纤维方向下裂缝尖端应力减值幅度(r0=0.5 mm,σ/τ=3)Table 2 ξn stress reduction amplitude of crack tip under different steel fiber direction (r0=0.5 mm, σ/τ=3)

4 结 论

本文在Eshebly等效夹杂理论与最大周向应力准则基础上，计算了无限大薄板上Ⅰ-Ⅱ复合型断裂应力强度因子及裂缝尖端最大应力比，解释了钢纤维角度对Ⅰ-Ⅱ复合型断裂韧度的影响机理。

(1)钢纤维增强水泥基复合材料通过改变裂缝尖端应变场，影响裂缝尖端应力强度因子，降低裂缝尖端的最大应力，延缓裂缝的开展，达到增韧效果。在Ⅰ-Ⅱ复合型断裂中，钢纤维方向与裂缝方向垂直时，裂缝尖端最大应力比降低最多，说明钢纤维定向后(β=0°)增韧效果最好。

(2)钢纤维方向与裂缝延伸方向垂直时，其他因素在此方向上的影响最敏感，表明钢纤维方向是影响水泥基复合材料断裂的最重要因素。钢纤维与竖直方向夹角β由0°增大到90°过程中，增韧效果先减弱后增强。

(3)在钢纤维方向与所受应力条件不变时，裂缝尖端与纤维水平投影的最小距离越小，裂缝尖端的最大周向应力越小，增韧效果越好。钢纤维弹性模量对裂缝尖端应力影响小，随着弹性模量的增加，裂缝尖端应力逐渐降低，增韧效果增强，但增韧幅度随弹性模量的增加而逐渐降低。