基于粗糙超立方体和离散粒子群的特征选择算法
王思朝,罗 川,李天瑞,陈红梅
(1.四川大学计算机学院,成都 610065;2.西南交通大学计算机与人工智能学院,成都 611756)
引 言
面对日益增长的数据维度和数据量,特征选择以其能够过滤冗余特征,对原始数据进行降维,进而提高学习效率和性能的特点,在文本挖掘[1]、图像处理[2]和信息检索[3]等诸多领域中都有着不可或缺的重要作用。一般来说,过滤式、封装式和嵌入式是目前特征选择主要的3 种方法。过滤式特征选择方法在评估特征质量时,往往以某种评价准则为依据排序特征,然后进行挑选,该过程与学习算法无关,如Laplacian 得分[4]、Constraint 得分[5]等,或是基于某种搜索策略对优化目标进行迭代求解,如基于前向搜索策略的mRMR[6]等。由于过滤式方法在特征选择过程中并不需要构建学习器对特征子集进行评估,因此拥有较高的选择效率。封装式方法会先通过某种搜索方法获取到特征子集,再由评价函数选取,最后采用学习算法对得到的特征子集进行评估。封装式方法中学习算法的选择不尽相同,如常用的决策树、贝叶斯等。该方法的求解结果比较好,主要是有学习算法的介入,但容易出现“过拟合”现象,即由贝叶斯选择出来的特征子集在决策树上的分类效果往往不如人意。此外,构建学习器对特征子集评估的开销较大,相对于过滤式会增加额外的时间消耗,从而效率低下。在嵌入式特征选择方法中,伴随着学习算法的构建,最优特征子集的求解也会一并进行,即把特征选择过程嵌入其中。但是由于嵌入式算法依赖于具体的学习算法,导致其通用性不佳[7]。
粗糙集理论以其在处理不精确和不完备数据的独特优势,为不确定性特征选择问题提供了一套系统的基于决策语义保持的理论框架[8]。经典粗糙集模型无法直接处理含有数值型数据的特征选择任务,所以需要离散数据,但这个操作不可避免地会丢失部分特征信息。针对这一问题,邻域粗糙集[9]、模糊粗糙集[10]以及粗糙超立方体[11]等扩展模型及方法被相继提出,并被引入到面向数值型数据处理的特征选择问题中。然而,目前基于上述模型和方法的特征选择算法中搜索策略均为前向搜索或后向消除的启发式策略,无法得到全局最优的特征子集。近年来,越来越多的元启发式(Meta⁃heuristic)算法与粗糙集理论相结合被应用于解决特征选择问题,特别是集群智能算法,包括粒子群优化(Particle swarm optimization,PSO)[12]、人工蚁群优化[13]等。Chen 等[14]通过条件与决策特征间的互信息定义出特征重要程度,进而提出了基于蚁群优化的特征选择算法;Yamany 等[15]采用灰狼优化算法作为搜索优化方法,设计了基于粗糙集正区域的特征选择算法;Chen 等[16]在邻域粗糙集模型框架下选择鱼群优化算法寻找最优特征子集,可以很好地处理数值型数据。
粒子群优化算法是集群智能算法中较为常用的方法之一。Wang 等[17]提出了一种基于粗糙正域的粒子群优化算法,对比采用基因算法的粗糙集特征选择算法有更好的表现;Bae 等[18]对传统的粒子群优化算法进行了改进,提出了一种新的称为智能动态集群的演化算法,同样也是基于粗糙正域,但平均效率高于文献[17]算法;Inbarani等[19]设计了一种基于粗糙集和粒子群优化算法的相对约简和快速约简算法,并应用于医学诊断;Zhang 等[20]提出了一种基于邻域粗糙集的离散粒子群优化算法,用于解决基因特征选择问题。由于基于前向搜索策略的粗糙超立方体方法只能得到局部最优结果,而计算所有特征子集组合开销过大,针对这一问题,本文将离散粒子群优化算法和粗糙超立方体方法相结合,提出了一种新颖的基于粗糙超立方体和离散粒子群的特征选择算法(Feature selection based on rough hypercuboid and binary PSO,FSRHBPSO)。该算法在粒子生成阶段引入了特征重要度这一先验知识,以提高收敛效率;并改进了粗糙超立方体的目标函数,消除了特征数量较多时导致特征相关度和重要度值过小的影响,用于优化函数;最后引入了线性递增的变异机制,使粒子不至于困入局部最优解而无法逃脱。
1 相关基础知识
本节阐述了粗糙超立方体方法的基本概念,并且介绍了离散粒子群的相关理论。
1.1 粗糙超立方体
假设论域U={u1,u2,…,un}是一个包含n个对象的集合,条件特征集C={A1,A2,…,Am}和决策特征集D={d}是一个非空的有限集合。由决策特征集D对论域U进行划分,得到等价类U/D={β1,β2,…,βc}。条件特征Ak∈C相对于第i个等价类βi的值域表示为区间[Li,Ui],该区间包含了所有属于等价类βi的对象在Ak下的特征取值。
给定特征Ak,假设论域U相对于决策特征集D有c个等价类,则定义超立方体等价划分矩阵为H(Ak)=[hij(Ak)],其中

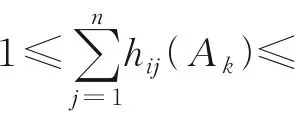
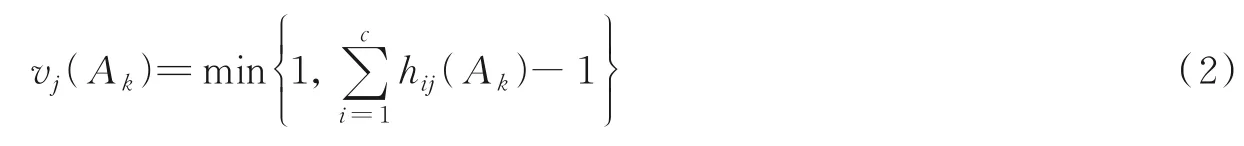
等价类βi在特征Ak下的粗糙近似集可由Ak的超立方体等价划分矩阵和混淆向量表示为

则等价类βi的边界域定义为
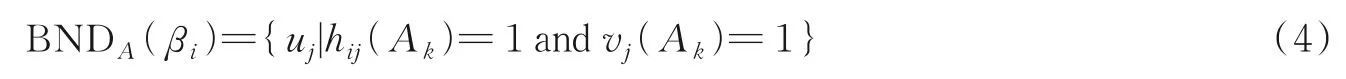
条件属性Ak和决策特征集D的依赖度定义为

式中0 ≤γAk(D)≤1。
给定两个条件特征Ak、Al,特征子集{Ak,Al}的超立方体等价划分矩阵可以计算为H({Ak,Al})=H(Ak)∧H(Al),其中hij({Ak,Al})=hij(Ak)∧hij(Al)。
因此特征Ak相对于特征子集{Ak,Al}的重要度为

式中0 ≤σ{Ak,Al}(D,Ak)≤1。
根据上述定义,可以得到一些特征评估准则,以选择出特征间具有高重要度,特征与决策类别具备高相关度和依赖度的最优特征子集。
假设S(S⊆C)为已选特征子集,则它与决策特征集D的平均相关度为

特征子集S的平均重要度为
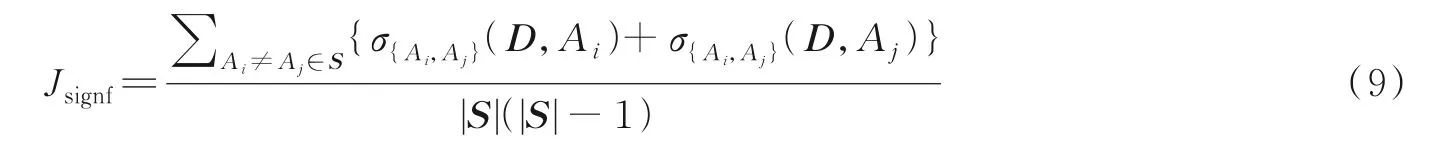
通过结合上述3 个特征评估准则可以构建出以下目标函数,用于挑选最优的特征子集,即

式中和λ为2 个权重参数。
特征选择过程可以采用一种较为流行的前向搜索策略。依据目标函数启发式地挑选特征,直到所选特征数量满足要求[11]。然而该方法搜索范围仅限于部分特征空间,所得结果也只能看做是局部最优。为了充分发挥粗糙超立方体方法的优势,依赖于离散粒子群优化算法在整个特征空间中的搜索能力,将两者相结合,提出了一个新的用于解决特征选择问题的组合优化算法,以挑选出全局最优的特征子集。
1.2 离散粒子群优化算法
PSO 算法是Kennedy 等在1995 年提出[12]。该算法中粒子通过不断学习自身和群体行为从而实现迭代优化,具体过程为:在D维的问题空间中,随机产生1 组粒子,每个粒子可以认为是该问题的1 种可行的解决方案,并且用向量Xi=(xi1,xi2,…,xiD)和Vi=(vi1,vi2,…,viD)分别描述第i个粒子的位置和速度。另外,第i个粒子和整个群体在优化搜索过程中,由目标优化函数计算得到的个体以及全局的最佳位置分别记作Pi=(pi1,pi2,…,piD)和Pg=(pg1,pg2,…,pgD)。搜索过程中,第i个粒子会依据式(11)和式(12)对其当前位置和速度进行重新计算,随机移动以寻找全局最优的解决方案,即


为了将PSO 算法从连续空间应用到离散搜索空间中的优化问题。Kennedy 等[21]进一步设计出Bi⁃nary PSO(BPSO)算法。其中,粒子的位置向量可以用二进制变量表示,即向量中的每1 位为1 或0。速度向量保持原有形式,不过其数值含义代表了粒子位置的某1 位将变为“1”的概率,由Sigmoid 函数式(13)将速度向量的连续值映射到[0,1],有

式中rand 为介于[0,1]间的随机数。将BPSO 应用于特征选择问题中,粒子位置向量的每一维就是1 个特征,值为1 表示特征被选择。因此某一维速度越大,该对应特征被选择的概率也就越高。
2 本文方法
本文方法中每1 个粒子代表1 种特征选择子集。针对随机生成粒子,缺乏先验知识这一问题,充分考虑了特征与决策类的相关度作为粒子初始化的依据。此外本文还结合特征相关度、依赖度和重要度这3 种标准在实验过程中的实际表现情况,对评价标准式(10)进行了改进,作为优化函数。鉴于合适的优化函数可以帮助优化算法挑选出性能最好的特征子集。本文还引入了遗传算法中的变异机制,进一步加强了粒子的搜索能力。
2.1 粒子编码
粒子群中每个粒子的位置向量对应1 个特征子集,那么分量就是1 个特征。分量的值仅为1 或0。当特征子集包含某个特征时,相应地分量值设为1,否则为0。所以二进制位串代表1 种特征选择模式,它的长度应该等于m,即原始特征的总个数。
2.2 粒子初始化
该阶段会初始化I个粒子,I代表粒子群中粒子个数。粒子初始化对于PSO 算法收敛速度和结果质量非常重要。不考虑先验知识,随机生成1 组粒子虽然在一定程度上有益于寻找最优结果,特别是处理一些高维的优化问题。但是不排除会出现一些粒子距离最优特征子集过远,使得优化算法收敛速度过慢。为解决该问题,本文在粒子初始化阶段考虑了特征与决策特征之间的相关度,并采用了概率的策略,位置向量的生成方法具体为
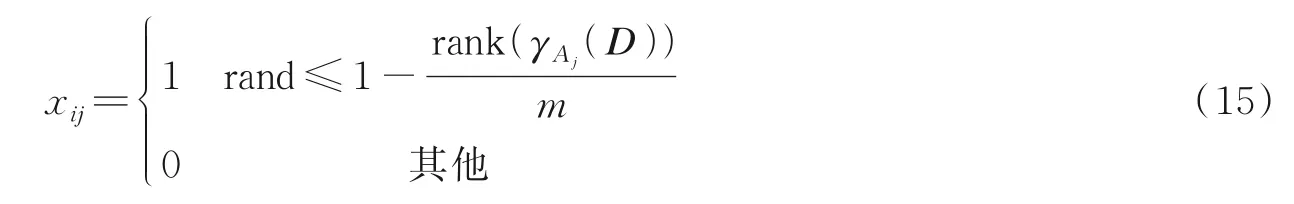
式中:xij为第i个粒子的第j维位置分量;γAj(D)为特征Aj与决策特征集D之间的相关度;rank(γAj(D))是指对所有特征的相关度降序排列后特征Aj相关度的序值。式(15)表明特征的相关度越高,那么该特征序值越小,被选择的可能性越高,该特征对应的位置分量为1 的概率也就越大。
2.3 参数设置
惯性权重w可以调节前一时刻的运动状态与现在时刻速度的关系,同时决定了粒子的局部和全局搜索能力。一般来说,希望粒子在前期能在特征解空间中快速找到最优特征子集的大致范围,然后再聚焦该范围,找出最优的特征选择子集。因此,本文选取了线性递减方法,其计算方式为

式中wmin和wmax为w的最小和最大值,需预先设定。式(16)说明粒子在迭代初始运动速度较快,全局搜索能力较强。当处于中后期时,速度会越来越小,有利于粒子很好地进行局部范围探索。
2.4 优化函数
优化函数决定了特征选择的质量,合适的优化函数能帮助BPSO 选择出更好的特征子集,即保证分类能力的同时保留更少的特征规模。式(10)中粗糙超立方体方法的目标函数虽然综合考虑了特征子集的平均相关度、依赖度和平均重要度,适合作为优化函数,但实验过程中,本文发现在处理实际数据集时,多数特征子集计算得到的平均相关度和平均重要度要远小于1,特别是所选择的特征子集中特征的个数较多时。这就使得目标函数中依赖度对特征子集的评估影响远大于平均相关度和重要度。出现这种情况的原因是3 种评价指标的取值范围不相同,结合式(7),平均相关度的取值范围为

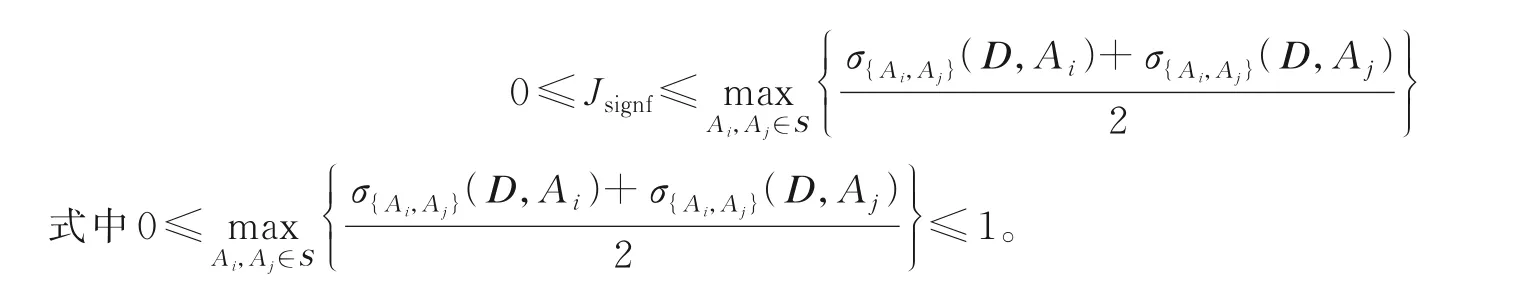
因此,为了保证3 种评价标准取值范围相同,提高平均相关度和重要度对评价特征子集的作用,本文选择将两者进行归一化。另外,为了减少特征重要度在迭代时的重复计算,保证算法效率,本文选择在迭代前计算出两两特征的重要度之和,用大小为m×m的特征重要度矩阵Sig={sigij}表示,其中

式中:1 ≤i,j≤m,sigij表示特征Ai相对于特征子集{Ai,Aj}的重要度与特征Aj相对于特征子集{Ai,Aj}的重要度之和。
因此,结合粗糙超立方体方法的目标函数式(10),粒子群的优化函数为

2.5 变异机制
BPSO 算法容易出现迭代后期陷入到局部最优的情形,而且该算法本身缺少逃脱局部最优解的机制,为了增加粒子搜索过程中的多样性,本文引入了线性递增的变异机制,有

式中:rmut为变异率;rmax、rmin为2 个预先设定值。可以看出,粒子的变异概率在优化过程中会越来越大,相应的局部搜索能力也会越来越强。
2.6 时间复杂度分析
算法1 概括了本文算法的主要步骤。在其运行过程中,第1 步需要计算每个特征的粗糙超立方体等价划分矩阵,该矩阵大小为n×c,c表示类别数,那么其时间复杂度为O(mnc)。同样地,第2 步中每个特征相关度的计算仍然基于粗糙超立方体等价划分矩阵,其时间复杂度同样为O(mnc)。第3 步中由于式(6)的计算只涉及两个粗糙超立方体等价划分矩阵的计算,时间复杂度为O(nc),而式(17)中特征重要度矩阵中有m2个元素,则其时间复杂度为O(m2nc)。在第(5)~(13)步中,主要计算部分为步骤6中的优化函数式(18),由于相关度和重要度已计算出,只需计算依赖度式(8)。而依赖度的计算与所选特征个数有关。最坏情况下,每个特征均被选中,这时对于每个粒子,式(18)所需要的时间复杂度为O(mnc),共有I个粒子,并进行了M次迭代,所以步骤(5)~(13)的时间复杂度为O(MImnc)。由以上分析可知,本文算法的时间复杂度为O(MImnc)。
算法1FSRHBPSO 算法
输入:决策信息系统DT=<U,C∪D>,原始特征个数m,最大迭代次数M,粒子个数I,学习因子c1,c2,粒子速度、惯性权重和变异率的最小和最大值,即Vmin,Vmax,wmin,wmax和rmax,rmin,权重参数和λ;
输出:特征子集S

3 实验与结果
本节选取了多个数据集和对比算法进行特征选择,并对所得子集用两种不同的分类器比较它们的平均性能。最终结果显示,本文算法在大多数情况上,可在保证分类质量的同时具备更少的特征数量。
3.1 数据集
为了更好地测试本文算法性能,本文从UCI数据库选择了6 个数据集,它们规模和维度不一,类别数目也有所差异,但均只包含数值型特征,具体描述如表1 所示。

表1 数据集描述Table 1 Details of datasets
3.2 参数和λ 的取值分析
将本文算法运行在表1 中不同的数据集上,实验中参数和λ的取值均从0.0 开始,以0.1 为间隔递增至1.0,共有11×11 种组合,例如,其余的实验参数如表2 所示。由于BPSO 算法运行结果具有随机性,为了避免偶然误差对实验结论的影响,本文算法在每个数据集和每种参数组合都进行了10 次实验。此外,本文还选用了Weka[22]中的C4.5 和Naive Bayes 两种分类算法,采用10 次十折交叉验证的方法用于分类精度的评估。图1 和图2 分别描绘了本文算法在不同的权重参数组合以及C4.5 和Naive Bayes 两种分类器下的平均分类精度和特征选择个数。从图1、2 中可以看出,随着参数逐渐减小,λ逐渐增大,除了图1(a)和图2(a)外,其余子图的分类精度都表现出逐步升高的整体趋势,并在接近该点处又呈现下降趋势。同样地,当参数逐渐减小,λ逐渐增大时,所有子图的颜色也在由蓝色逐步过渡到橙色,表明特征选择的个数也在逐渐增加。结合优化函数式(18)可发现减小、λ增大时,特征子集依赖度的权重变大,会引起分类精度的提高,同时特征数量也会增加。虽然本文算法在不同数据集同一分类器或同一数据集不同分类器上取得最优分类精度的权重参数值都不统一,但是在和λ∈[0.6,0.9]时,大多数数据集在特征个数较少的同时,拥有较高的平均分类精度。
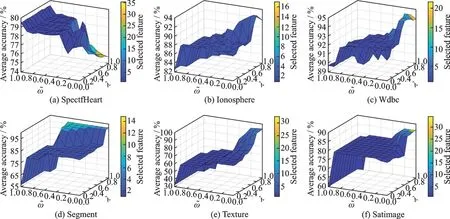
图1 FSRHBPSO 算法在6 个数据集(C4.5 分类器)不同的参数和λ 组合下的平均分类精度和特征选择个数Fig.1 Average classification accuracy and the number of selected features over 6 datasets with C4.5 classifier and the different combinations of parameters and λ

图2 FSRHBPSO 算法在6 个数据集(Naive Bayes分类器)不同的参数和λ组合下的平均分类精度和特征选择个数Fig.2 Average classification accuracy and the number of selected features over six datasets with Naive Bayes classifier and the different combinations of parameters and λ

3.3 分类精度实验比较与分析

表2 4 种算法的参数设置Table 2 Parameter settings of four algorithms
由于RS⁃PSO 和RS⁃IDS 算法无法直接处理数值特征,本文选择Weka 工具中有监督的Kononenko离散化方法,对实验所用数据集进行离散。同样地,为了避免随机误差对实验结果的影响,除RH 算法外的5 种算法在每个数据集上均进行10 次独立地特征选择。表3 比较了在所有数据集上,5 种算法10次选择结果的平均特征个数(avg)和不同结果个数(diff),其中平均个数最小的结果加粗表示。此外,由于NRS⁃DPSO 算法的优化函数是基于正区域的,所以当生成的粒子群在迭代优化过程中不存在与条件特征集合的正区域相等的粒子时,便会无法得到有效的特征子集,结果为空集,这里用“-”表示。同时由于RH 算法需要指定特征选择的个数,除了数据集Texture 设置为7 外,其余数据集上均与本文算法所选特征个数保持一致,以验证在相同特征子集大小下,本文算法是否有更好的性能。
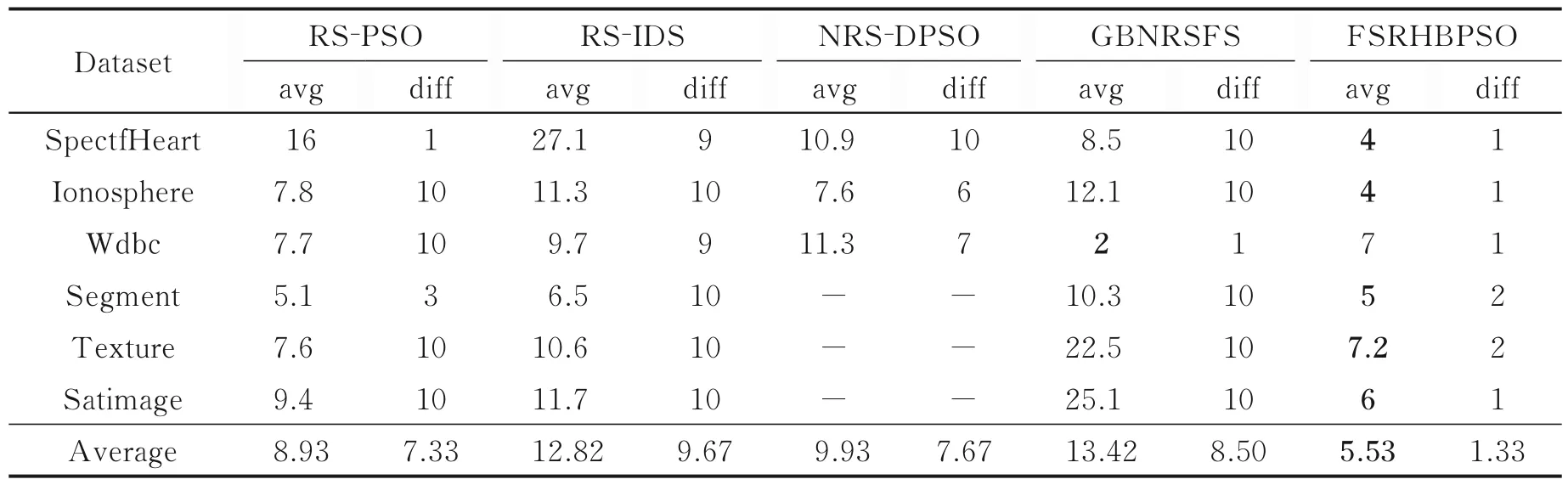
表3 特征子集大小比较Table 3 Comparison of the number of feature subsets
从表3 可以看出,就平均特征个数而言,本文算法在6 个数据集的特征个数都要少于RS⁃PSO、RS⁃IDS 和NRS⁃DPSO 算法,特别是在SpectfHeart 数据集上,本文算法的约简率为9.09%,而RS⁃PSO、RS⁃IDS 和NRS⁃DPSO 的约简率分别为36.36%,61.59%和24.77%。以外,除了在Wdbc 数据集上,本文算法的特征选择个数均小于GBNRSFS 算法,尤其是在数据集Texture 和Satimage 上,GBNRSFS 算法的约简率分别是56.25%和69.72%,而本文算法的约简率仅为18%和16.67%。就10 次选择结果中不同特征子集个数而言,RS⁃PSO、RS⁃IDS 和NRS⁃DPSO 三种粒子群算法的平均值分别为7.33,9.67 和7.67。这是由于它们很容易陷入局部最优解,从而导致10 次独立实验最终收敛的结果各不相同。而GBNRSFS 算法的值为8.5,这是其中k⁃means 算法聚类结果的不确定造成的,从而使得特征选择结果并不统一。而本文算法除了在数据集Segment 和Texture 上得到2 种不同的特征子集外,在其余数据集上均只有1 种结果,这是因为本文算法中的变异机制允许粒子以一定概率逃脱局部最优,从而可以收敛到全局最优的情况。总的来说,本文算法相对于其余算法具有较强的稳定性和全局搜索能力。本文进一步对6 种算法的特征选择结果进行平均分类精度的比较,同样用到了Weka 中的C4.5 和Naive Bayes 两种分类器和10 次十折交叉验证的方法。表4、5 列出了6 种算法的特征子集分别在C4.5 和Naive Bayes分类器上平均分类精度的比较结果。

表4 特征子集在C4.5 分类器上平均分类精度的比较Table 4 Comparison of average classification accuracy of feature subsets using C4.5 classifier
从表4 结果来看,在C4.5 分类器的平均分类精度上,本文算法只有在Texture 和Satimage 数据集上略低于GBNRSFS 算法,但是结合特征选择个数来看,本文算法在特征选择个数约为GBNRSFS 算法特征个数的1/3 和1/4 的情况下,与其平均分类精度仅相差0.878 6%和0.038 2%,不足1%。在6 个数据集上,相对于其余4 个对比算法,本文算法的平均分类精度都要更高。具体来说,本文算法在Ionosphere 上相对于RH、RS⁃PSO、RS⁃IDS、NRS⁃DPSO 和GBNRSFS 算法的平均分类精度分别提高了1.604 0%,3.438 7%,4.025 8%,2.287 7%和5.868 9%。从平均结果上看,本文算法的平均分类精度相对于RH、RS⁃PSO、RS⁃IDS 和GBNRSFS 算法分别提高了1.889 2%,1.318 2%,1.718 6%和1.237%;在前3 个数据集上,本文算法比NRS⁃DPSO 也有1.157 2%的提升。
同样地,表5 结果显示本文算法在Naive Bayes 分类器上仍然优于其他算法,尤其是在Segment 和Texture 两个数据集上。在Segment 上,本文算法相对于RH、RS⁃PSO、RS⁃IDS 和GBNRSFS 算法的平均分类精度分别有5.747 2%,5.224 6%,10.167 5%和10.582 3%的提高;在Texture 上,相对其他算法分别提高了7.592 2%,3.300 9%,8.302%和4.852 9%。最后从所有数据集的平均结果来看,本文算法相对于RH、RS⁃PSO、RS⁃IDS 和GBNRSFS 算法仍有较大幅度的优势,具体为3.186 0%,3.058 4%,4.682 8%和6.408 5%;在前3 个数据集上,NRS⁃DPSO 的平均分类精度要低于本文算法3.108 9%。总体而言,在多数数据集上,FSRHBPSO 算法在C4.5 和Naive Bayes 分类器的表现都要优于另外5 种算法。

表5 特征子集在Naive Bayes 分类器上平均分类精度的比较Table 5 Comparison of average classification accuracy of feature subsets using Naive Bayes classifier
4 结束语
本文采用了适用于二元空间的离散粒子群优化算法,引入粗糙超立方体方法中相关度的概念在粒子初始化阶段加入了先验知识;同时添加变异机制,丰富了优化算法搜索过程中的多样性。此外还根据实验过程中粗糙超立方体3 种评估标准的实际表现情况,对目标函数进行了改进,并将改进后的目标函数与离散粒子群优化算法相结合,设计了新的基于离散粒子群和粗糙超立方体的特征选择算法。最后实验结论表明该算法能在保证分类质量的同时选择出数量更少的特征子集。同时相比前向搜索策略的粗糙超立方体方法及其他粒子群算法具有更好的性能。下一步工作考虑将该算法与云计算相结合,以增强算法面对大规模数据的计算能力。

