塔脚板底板接触应力非线性分布及弯曲应力表达式

钱小浩，杨垂玮，刘浩，黄模佳

(1.南昌大学工程力学研究所，江西 南昌 330031；2.中国能源建设集团安徽省电力设计院有限公司，安徽 合肥 230601)

塔脚板作为电路线路建设中的重要基础构件，随着工业用电量的急剧增加，提高输电铁塔的承载力对于我国电力发展迫在眉睫，塔脚板的形式也从一开始的无加劲发展到单边加劲，再到现在的双边加劲[1]。工程中目前较为常用的塔脚板类型是无加劲踏脚板与单边加劲式塔脚板，其中无加劲踏脚板结构较为简单，加工、安装更为便利，因而在实际工程中的应用也最为广泛。当塔脚板处于受压工况时，输电线路塔所受的荷载通过塔脚板底板传导给下部基础。目前工程中，将踏脚板与混凝土接触处的应力分布按经验近似为平均分布，这种近似结果与实际结果相差较大，不能真实反映接触处的应力分布情况，对工程指导价值有限。为更接近实际情况，在传导过程中，塔脚板底板与混凝土基础之间考虑非线性接触，得到的应力场分布更符合实际，对实际工程实践更具有指导作用。现行的工程设计规范《架空输电线路杆塔结构设计技术规定》[2]并未给出塔脚板与混凝土接触处的应力场分布规律，而工程中亟须了解塔脚板应力分布情况，以对踏脚板进行相应的改善，达到安全、经济、适用的目的。因此，研究塔脚板在受压工况下的应力场分布成为电力行业的重要任务之一。

相较于国外，我国的用电需求与电压等级要求较高，经过多年的研究与工作总结，我国对输电线路设计方面有相对深刻的认识。国内的学者对塔脚板的结构设计做了大量工作与研究，并在这基础上取得一定的研究成果[3-8]。刘俊卿等[3]对四地脚螺栓塔脚板进行了相应的研究，得出了四地脚螺栓塔脚板在荷载作用下，底板与靴板、加劲板连接处的应力分布情况；底板厚度的增加能大大提高承载力，据此对厚度计算提出了新的计算表达式。杨攀等[5]对单角钢八地脚踏脚板厚度进行研究，分析了踏脚板的受力状态及传力机制，并给出踏脚板厚度计算表达式。以上建议能较好地指导工程实践，但刘俊卿等只对踏脚板的连接处进行应力分布研究，杨攀等给出的厚度表达式基于八地脚踏脚板，分析了不同厚度下塔脚板危险点的应力状况，两者皆未指出踏脚板与基础接触处的应力分布情况。

鉴于以上研究背景与工程实际，本文采用常用的四地脚无加劲塔脚板为研究对象，在受压工况下，考虑与混凝土基础之间的非线性接触，分析混凝土表面应力场分布规律。在此基础上，给出受压方型塔脚板在不同厚宽比下的应力分布情况，并利用有限元进行校核对比。最后，基于上述研究，给出不同的厚宽比下应力场分布表达式以及最大弯矩表达式，并将各厚宽比表达式系数汇总成系数表，为工程实践提供指导作用。

1 四地脚螺栓塔脚板弯曲应力表达式推导

根据板壳理论[9]，取1/4四地脚螺栓塔脚板进行研究，见图1。其固定端的挠度和转角均为零，边界控制条件满足：

图1 塔脚板简化模型

(1)

(2)

基于里兹法，可将位移函数w表示为：

w=a1φ1(x，y)+a2φ2(x，y)+…+anφn(x，y)

(3)

利用薄板的直法线假设和边界条件要求，利用式(1)～式(3)建立含10个系数且符合上述条件的位移方程w：

w=a1x2y2+a2x3y2+a3x2y3+a4x4y2+a5x3y3+a6x2y4+a7x5y2+a8x4y3+a9x3y4+a10x2y5

(4)

将位移方程w分成两部分：

φ(x，y)=x2y2，φ(x，y)=a1+a2x+a3y+a4x2+a5xy+a6y2+a7x3+a8x2y+a9xy2+a10y3

(5)

(6)

(7)

当塔脚板为压工况时，塔脚板的外力势能为：

(8)

总势能为：

E=U1-V

(9)

式中：E为系统的总势能；U1为板的变形能；V为塔脚板的外力势能；q为应力分布函数。

把挠度方程式(6)代入式(9)中：

(10)

式中：D为挠曲刚度；β为积分影响系数，不同厚宽比对应不同积分影响系数。

根据最小势能原理，利用式(10)对ai依次进行求导，为得到a的转置矩阵，引出A，H矩阵，计算步骤如下：

(11)

通过以上计算可得出A，H矩阵

A，H矩阵与式(7)中的a矩阵之间满足：

a=A-1H

(12)

式(8)中，只有b矩阵里面含变量，求底板固定端最大弯矩Mx只需对b矩阵求导：

(13)

(14)

由于两个固定端的最大弯矩相等，取一边的最大弯矩即可，此处取Mx：

(15)

2 受压四地脚螺栓塔脚板模型有限元仿真

2.1 塔脚板结构及有限元模型

为了探究四地脚螺栓塔脚板与基础考虑非线性接触时压工况下的应力场分布，现通过参数化建模，建立不同厚宽比底板的塔脚板来观察竖向压力下的应力分布，四地脚螺栓塔脚板参考某电力院采用的输电塔塔脚的四地脚螺栓塔脚板，角钢与塔脚板材料采用Q345钢，弹性模量设置为206 GPa，泊松比为0.3；混凝土基础材料采用C30混凝土，弹性模量设置为30 GPa，泊松比为0.2。

利用Abaqus有限元软件分析计算。为简化模型，忽略螺栓孔、锚杆以及螺杆。角钢与塔脚板为绑定约束，塔脚板与基础表面为接触约束(切向行为为罚摩擦系数0.3，法向行为为硬接触)[10-12]，角钢和塔脚板网格划分采用20节点2次六面体单元，单元尺寸为10，此单元有很好的模拟精确性；混凝土采用8节点六面体单元用来模拟三维实体，单元尺寸为20。有限元模型见图2。

图2 有限元模型图

建立耦合点，此耦合点位于四地脚螺栓塔脚板形心正上方，通过耦合角钢上表面，模拟荷载直接通过角钢加载到四地脚螺栓塔脚板，加载力为1 000 kN。在满足规范设计的情况下，塔脚板底板宽度不变，改变底板厚度设置5组不同厚宽比的模型依次为0.06，0.07，0.08，0.09，0.10。与塔脚板(厚宽比0.10，0.06)接触的混凝土表面应力σ见图3～图4。

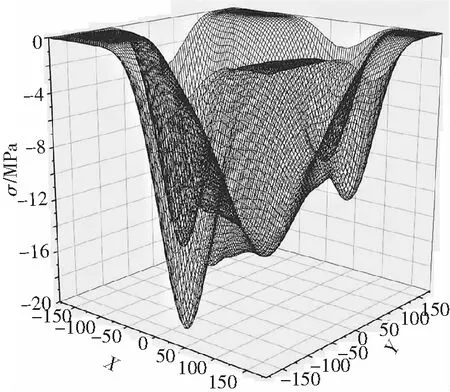
图3 γ=0.10时压应力图

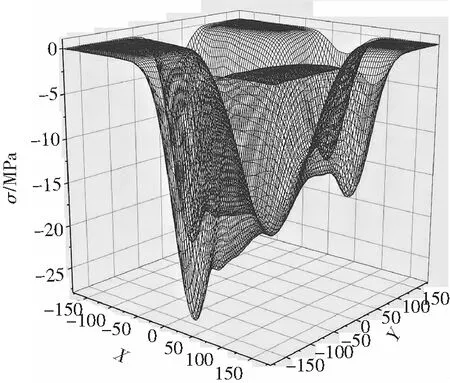
图4 γ=0.06时压应力图

2.2 有限元仿真结果分析

提取5个模型底板的压应力分布云图，可以看出压应力主要分布在靴板附近，而主角钢区(见图1)的压应力相比较大。厚宽比增大时，角钢附近的压应力逐渐减小，但相对角钢附近的作用区域有所增大，非角钢作用区压应力值有所增加。为探究靴板附近区块应力占比，以靴板为中心参考，当区块宽度与靴板厚度比值为1时，即靴板下方区域。

从表1可以看出：当不同厚宽比下，靴板区域的压力占比依次为23.3%，21.4%，19.5%，18%，16.9%。宽厚比越大，靴板下方的压力占比越小，这部分的压力在受压时不会对靴板产生弯矩，当区域宽度与厚度之比为4时，随着厚宽比从0.06增至0.10时，压力占比逐渐从72.7%，68.5%，63.5%减至55.3%。当区块宽度与厚度之比达到8时，在厚宽比为0.06时，区域所受压力已经占加载压力的92.1%，除此之外的区域基本不受压力。厚宽比增加时，压力占比降到83.2%，仍占压力分布的绝大部分。厚宽比影响着四地脚螺栓塔脚板底部应力分布，表现为厚宽比越大，压力主要作用区越大，最大压应力值有所下降。

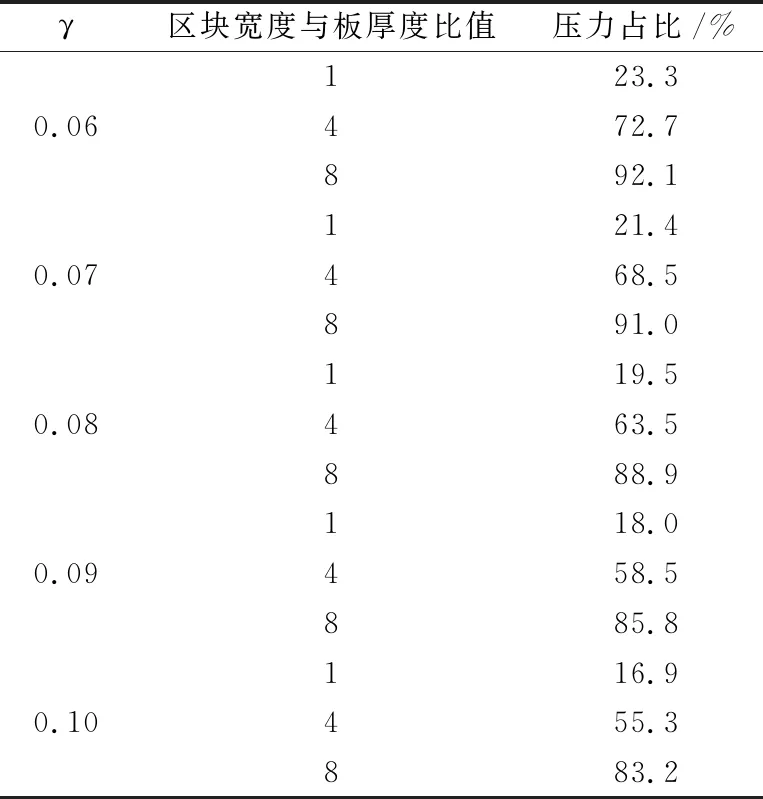
表1 不同宽厚比下压力占比

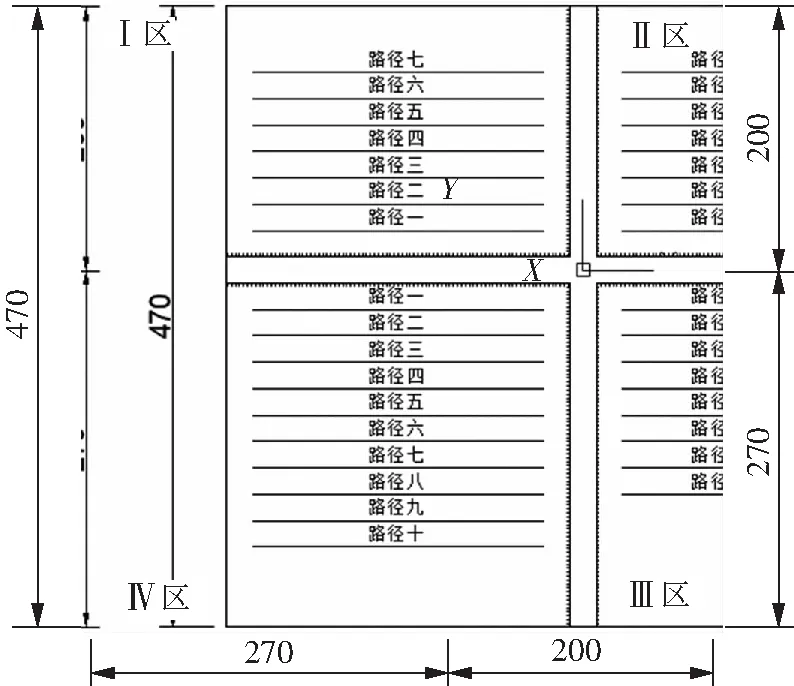
图5 底板分区及路径图

(16)

表2 各厚宽比下Ⅳ区拟合表达式q系数

提取5个不同厚宽比下Ⅳ区的压应力云图(不考虑靴板正下方压应力)，得出不同厚宽比下Ⅳ区压应力平均值σ平均为-3.59，-3.48，-3.37，-3.21，-3.06 MPa。

(17)

c0=c1=-314.286γ2+80.750γ-3.060

(18)

c2=854.857γ2-75.135γ-10.999

(19)

c3=c4=154.929γ2-94.590γ+8.802

(20)

其中：F为加载力；A为底板面积；γ为底板厚宽比。图5为c1，c2，c3关于γ拟合的曲线。

图6 c1，c2，c3拟合图

2.3 有限元仿真结果校核

5个模型施加的压荷载皆为1 000 kN，不同厚宽比对应不同的接触应力表达式，所以需要压力F与q的表达式，使得所拟合的表达式适用于工程应用。提取各厚宽比下Ⅳ区的压应力云图，乘以Ⅳ区面积得到相应的压力依次为-242 954，-235 248，-227 812，-216 996，-206 720 N，由于下压力主要集中在靴板附近区，所以只对靴板附近作用区进行积分。

当厚宽比γ为0.10时：

当厚宽比γ为0.09时：

当厚宽比γ为0.08时：

当厚宽比γ为0.07时：

当厚宽比γ为0.06时：

表达式中q0.10，q0.09，q0.08，q0.07，q0.06分别为表2中Ⅳ区中q的表达式，A4为Ⅳ区面积。

现将厚宽比为0.10数据代入进行计算，拟合压力结果F0=-240 550 N与有限元计算所得F0=-242 954 N相差2 404 N，误差为0.99%。将各厚宽比下拟合结果值与有限元值进行对比，整理成表3。

表3 不同厚宽比下Ⅳ区压力有限元值与拟合值对比

从下压力F与q的表达式拟合计算所得数据看出拟合所得值与通过有限元计算的值十分接近，说明拟合的表达式精确度较高，最大误差约为6%。利用上述方式可得q0.10，q0.06Ⅰ区，Ⅱ区，Ⅲ区相应的系数，其他厚宽比下的各系数可根据q0.10，q0.06系数表进行线性插值近似计算。汇总系数表如表4。

表4 各厚宽比下Ⅰ，Ⅱ，Ⅲ区拟合表达式q系数

3 理论弯矩值与有限元弯矩值校核

基于里兹法，对不同厚宽比下非线性接触力的分布表达式进行校核。厚宽比为0.10时，绝大部分压应力作用区在靴板附近，而远离靴板区域应力值很小，该区域对靴板处产生的弯矩可忽略不计。不同厚宽比下，压应力主要作用区的宽度不一样，引入式(8)中的影响系数β。根据有限元模拟计算，塔脚板底板厚宽比0.06～0.10，所对应的最大弯曲应力值分别为105，94，83，69，63 MPa。

H=q0(hC)T

其中，

得出当厚宽比γ为0.10时的弯矩表达式：

M=(kc)2q0(0.040 5+0.010 2c0+0.032 5c1+0.006 87c2+0.004 34c3+0.027 2c4)

(21)

将式(17)～式(20)代入M：

M=k2(0.921+1.423γ-23.116γ2)(0.112-2.661γ2-0.052γ)F

式中:c为底板宽;k为Ⅳ区与底板宽度比值;F=1 000 kN，代入弯矩表达式，求出弯矩值为-220 25 N·m与有限元计算值-23 194 N·m相差5%，可以看出拟合出来的弯矩表达式较为精确。其他厚宽比下的M采用同样方法计算。

厚宽比γ为0.09时的弯矩表达式：

M=k2(0.921+1.423γ-23.116γ2)(0.097 7-2.409γ2-0.055 1γ)F

厚宽比γ为0.08时的弯矩表达式：

M=k2(0.921+1.423γ-23.116γ2)(0.082-2.067γ2-0.057 5γ)F

厚宽比γ为0.07时的弯矩表达式：

M=k2(0.921+1.423γ-23.116γ2)(0.066-1.702γ2-0.051 5γ)F

厚宽比γ为0.06时的弯矩表达式：

M=k2(0.921+1.423γ-23.116γ2)(0.049-1.349γ2-0.026γ)F

将各γ值代入相应的弯矩表达式，并进行拟合，函数设为M=k2(k1γ2+k2γ+k3)F，Maple拟合结果见式(22)：

M=k2(-10.571γ2+2.387γ-0.066 2)F

(22)

采用上述方式，求出不同厚宽比下Ⅳ区弯矩值M0。并与有限元弯矩计算值M1对照，结果整理成表5。

表5 有限元值与拟合值对比

(23)

式中:t为底板厚；k为Ⅳ区与底板宽度比值；c为底板宽；F为加载力；f为塔脚板许用强度。

弯矩积分影响系数β实质为四地脚螺栓塔脚板受压时，不同宽厚比所对应底板受压的范围。当厚宽比较大时，对应的压应力作用区较大，即主要产生弯矩的作用区较大；随着厚宽比的降低，对应的压应力作用区变小，弯矩积分影响系数下降，对应的弯矩相应下降。从拟合情况看，误差分别为5%，2.6%，0.6%，1%，6%，在工程可接受范围内。造成误差是因为不能精确求出不同厚宽比对应的弯矩积分影响系数β，可通过多次积分降低误差。

4 弯矩表达式及工程试验校核

基于上述对塔脚板与混凝土基础接触应力的研究，考虑两者之间的非线性接触，采用里兹法、有限元仿真及数据拟合，得出塔脚板Ⅳ区与混凝土基础间的压应力分布表达式q以及塔脚板底板最大弯矩表达式M：

(24)

M=k2(-10.571γ2+2.387γ-0.066 2)F

(25)

式中：q0，c0，c1，c2，c3，c4见式(17)～式(20)；k为Ⅳ区与底板长度比值;γ为底板厚宽比。

为验证上述表达式具有通用性，能够适用于其他规格的塔脚板，现采用某电力院实际工程塔脚板2E2-SZ1-14为实例进行真型足尺试验[14-15]，将有限元结果与真型试验结果对比，验证上述塔脚板q，M表达式，有限元模型的参数设置与2.1节类似。在某大学力学实验中心的微机控制电液伺服万能试验机上开展整体节点的真型试验。根据有限元计算结果，最大弯曲应力发生在靴板附近，试验中的应变片沿靴板垂直布置[16]。塔脚板试件底板具体尺寸为330 mm×330 mm×20 mm，γ=0.06，其底板Ⅳ区尺寸为188 mm×188 mm，荷载F为800 kN。

图7 2E2-SZ1-1模型

图8 试件实图

图9 测点图

图10 试验加载图

图11 荷载-应力图

表7 有限元值与计算值对比

通过对实际工程塔脚板2E2-SZ1-1的数值模拟分析与试验研究，得出的压应力值和弯矩值与本文表达式所计算的压应力值和弯矩值误差较小，三者结果较为接近。因此本文给出的表达式精确度较高，在实际工程中能够适用于其他规格的无加劲四地脚螺栓塔脚板。

5 结论

(1) 四地脚螺栓塔脚板在受压时，应力分布主要聚集在靴板附近，其应力占比约为90%。越靠近靴板，应力越大。通过压应力云图可知，当超过靴板厚度八倍的范围，压应力值几乎为零。

(2) 通过对四地脚螺栓塔脚板进行分析，最大弯矩出现在靴板与底板连接处，靴板正下方压应力不产生弯矩。通过压应力云图，压应力危险区出现在主角钢区，即Ⅳ区，建议在实际工程中通过增加底板或靴板厚度，加强主角钢区的强度。

(3) 四地脚螺栓塔脚板厚宽比影响底板应力分布，厚宽比越大，压力主要作用区越大，最大压应力值有所下降。在满足构造要求下，可通过加厚塔脚板厚度降低压应力。

(4) 利用有限元分析和Maple进行数值拟合所得的非线性压应力函数表达式，能够较好地与里兹法计算结果吻合，验证了非线性压应力表达式的可靠性，填补了DL/T 5154—2012《架空送电线路杆塔结构设计技术规定》关于塔脚板与混凝土接触处应力分布的空白，能够更好地给工程实践提供参考价值。