椭圆缩放管换热性能数值分析

李慧君，李 东

(华北电力大学 能源动力与机械工程学院，河北保定 071003)

0 引言

换热器是进行热量交换的节能设备，广泛应用于化工、石油、电力等工业领域。提高换热器换热效率能够提高能源利用率、减少能源消耗[1-2]。改变换热管型是提高换热器性能的有效手段，其中，缩放管是一种管径规律变化的高效换热管型，缩放管通过管径的周期性变化加强流体扰动，从而提高了换热性能。国内外学者对缩放管的流动换热特性进行了深入研究，王旭等[3]利用场协同理论对等截距缩放管的传热特性进行了分析，结果表明：雷诺数在4 138～5 977范围内，努塞尔数和压降随缩放角的增大、喉径比的减小而增大；陈志静等[4]采用数值模拟的方法，对不同肋高和扩缩比的6种缩放管进行了研究，结果表明，肋高e=1 mm、缩放比为2时，缩放管的综合性能最佳；王红兵等[5]对脉动流和缩放管的复合传热进行了数值模拟，分析了流体入口平均流速、缩放管的缩放比、肋高、脉动流的脉动振幅、脉动频率等5个参数对缩放管传热和沿程阻力的影响，得出脉动频率对缩放管综合性能影响最大、肋高影响最小的结论；HUANG等[6]对4种不同参数的缩放管的降膜蒸发进行了试验研究，结果显示，缩放管在高液膜雷诺数的条件下，传热系数较同直径光滑管更高，提高肋高能够增强液膜扰动，并对试验数据进行了关联式的拟合；崔凯[7]对3种缩放管进行了模拟计算，对其性能进行分析，并提出一种新的换热性能评价指标，即对流换热系数与单位面积克服阻力引起压力降的比值；朱孟帅等[8]对缩放管进行了详细地解释，分析了缩放管的工作原理，并对目前强化换热方法进行了总结；ZANGANA等[9]对缩放涡管和普通涡管的最大冷却点进行了试验和模拟，结果表明，减小缩放管的喉径能够有效提高涡流管的制冷量；王飞扬等[10-13]分析了椭圆管的强化换热，通过改变翅片椭圆管中翅片参数以及椭圆管排布方式，得到研究范围内的最优换热管型；张雨晨等[14]利用有限元法对扭曲椭圆管的力学性能进行了分析，得到扭曲椭圆管的轴向稳定性计算表达式；陈佳等[15]对翅片缩放管进行数值模拟，分析了翅片对蓄热体传热性能的影响，得到一定条件下提高肋片高度能够提高蓄热体蓄放热性能的结果。

现有研究多针对圆形截面缩放管及翅片椭圆管各参数对综合换热性能的影响。为探究椭圆形截面缩放管换热性能的优劣，文中通过改变扩缩比、长短轴比、雷诺数等参数对椭圆形截面缩放管(ECD)进行数值模拟，以丰富不同截面缩放管的研究，为高效换热器的设计提供一种新思路。

1 物理模型及边界层网格划分

1.1 建立几何模型

建立多种不同扩缩比γ(γ=L1/L2)、长短轴比a/b的等长三维椭圆缩放管。截面周长均与直径20 mm的圆管相同。各管型参数如表1,2所示。由于金属导热系数远高于流体，因此在绘制模型时忽略管壁厚度，几何模型及局部截面如图1,2所示。

表1 几何模型参数Tab.1 Geometric model parameters

表2 长短轴比Tab.2 Aspect ratios

图1 椭圆缩放管几何模型

图2 轴向局部、径向截面几何模型Fig.2 Geometric model of axial partial and radial cross-section

1.2 建立数学模型

假设流体为不可压缩流体，物性参数设为常数，流动为定常流动。其稳态连续性、动量、能量方程[3]分别为：

(1)

(2)

(3)

Realizablek-ε湍流模型：

(4)

(5)

(6)

式中,K为湍流动能，J；μt为湍流粘性系数；σk,σε分别为湍流动能和耗散率对应的普朗特数；Gk为速度梯度引起的湍流动能项，J；ε为耗散率；C1,C2为黏性系数；i,j为下角标，取值为1,2,3，分别代表x,y,z三个方向。

1.3 边界层网格划分

几何模型进行离散化处理，对计算区域划分四面体非结构网格。在近壁面处，由于温度梯度变化较大，采用适合高雷诺数的非平衡壁面函数对该区域流场进行计算。非平衡壁面函数要求第一层网格的节点处在核心湍流区域。因此，在计算第一层网格高度时，预设y+=30。水力直径随长短轴比的降低而增大，其计算式[16]为：

D=4A/C

(7)

计算第一层网格高度需要求解雷诺数Re、壁面摩擦系数Cf、壁面剪切应力τw、剪切速度uτ。第一层网格高度计算式[17]为：

y=(y+μ)/(uτρ)

(8)

2 网格无关性验证及边界条件设置

2.1 网格无关性验证

在管长L=500 mm、长短轴比为1.67、Re=16 000条件下，建立网格数为956 000，1 512 000，1 956 000的3种椭圆管模型进行网格无关性验证。以出口平均温度为评价指标，网格数为1 512 000和1 956 000时，误差约为4%。此时计算结果基本不受网格数影响。因此，后续计算过程中网格数量均约为1 512 000。

2.2 边界条件设置

湍流模型选择Realizablek-ε模型，这是因为该模型适应于二次流、旋流等复杂流动，压力和速度耦合采用SIMPLEC算法，其他均采用二阶迎风差分格式。入口边界条件采用速度入口、出口边界条件采用压力出口，壁面设为绝热壁面。

湍流强度计算式[18]为：

I=0.16Re-1/8

(9)

为保证计算精度，能量方程收敛值设置为1×10-6，其他方程设置为1×10-5。

3 数值模拟准确性验证

以直径为20 mm圆管为例，采用上述数值计算方法进行可行性分析。在Tw=373.15 K，雷诺数为16 000～22 000、入口温度为300 K、管内流体为水的条件下，分别计算努塞尔数Nu和阻力系数f，与Gnielinski关联式和弗罗年柯关联式[19]进行对比。努塞尔数的最大误差约为3.5%，阻力系数的最大误差约为6.2%，并且两参数的误差均随雷诺数的增加而降低。结果表明该模型具有可行性，对比结果如图3,4所示。努塞尔数模拟值比Gnielinski公式大，这是因为模拟时的壁面设为恒定壁温，忽略了壁面散热；阻力系数模拟值比弗罗年柯公式小，是因为模拟时的壁面设为光滑壁面，壁面阻力变小。

图3 努塞尔数Nu验证Fig.3 Verification of Nusselt number

图5 试验系统示意Fig.5 Schematic diagram of experimental system

文献[20]对缩放管传热特性和阻力进行研究，缩放管的几何尺寸：内径22 mm、扩张段6 mm、收缩段15 mm、节距41 mm，试验系统见图5。

以试验中缩放管参数绘制三维模型并进行数值计算，将模拟得到的阻力系数f与试验数据进行对比，结果如图6所示。可以看出，阻力系数f的模拟值与试验值趋势近乎相同，并且最大误差约为6%，基本符合计算需要。

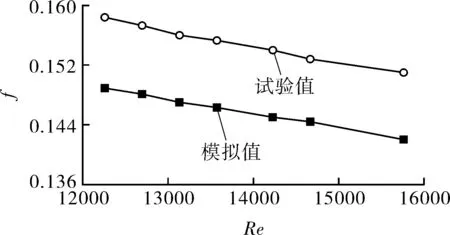
图6 模拟值与试验结果对比Fig.6 Comparison between simulated values andexperiment results

4 计算结果分析

4.1 长短轴比对换热性能的影响

以水为管内介质，在扩缩比为3∶1，节距为4 mm，Tw=373.15 K、温度为300 K的条件下，取普朗特数Pr=6.99,Re=16 000,19 000,22 000,对长短轴比为2,1.67,1.43,1.25,1.11的椭圆缩放管进行数值模拟。长短轴比的改变会影响管轴向截面形状,长短轴比越大截面形状越扁平，截面面积越小。在雷诺数一定的条件下，周长相等的管型流量相等[21]。利用场协同数对换热性能进行评价分析,场协同数计算式[22]为：

Fc=Nu/(Re·Pr)

(10)

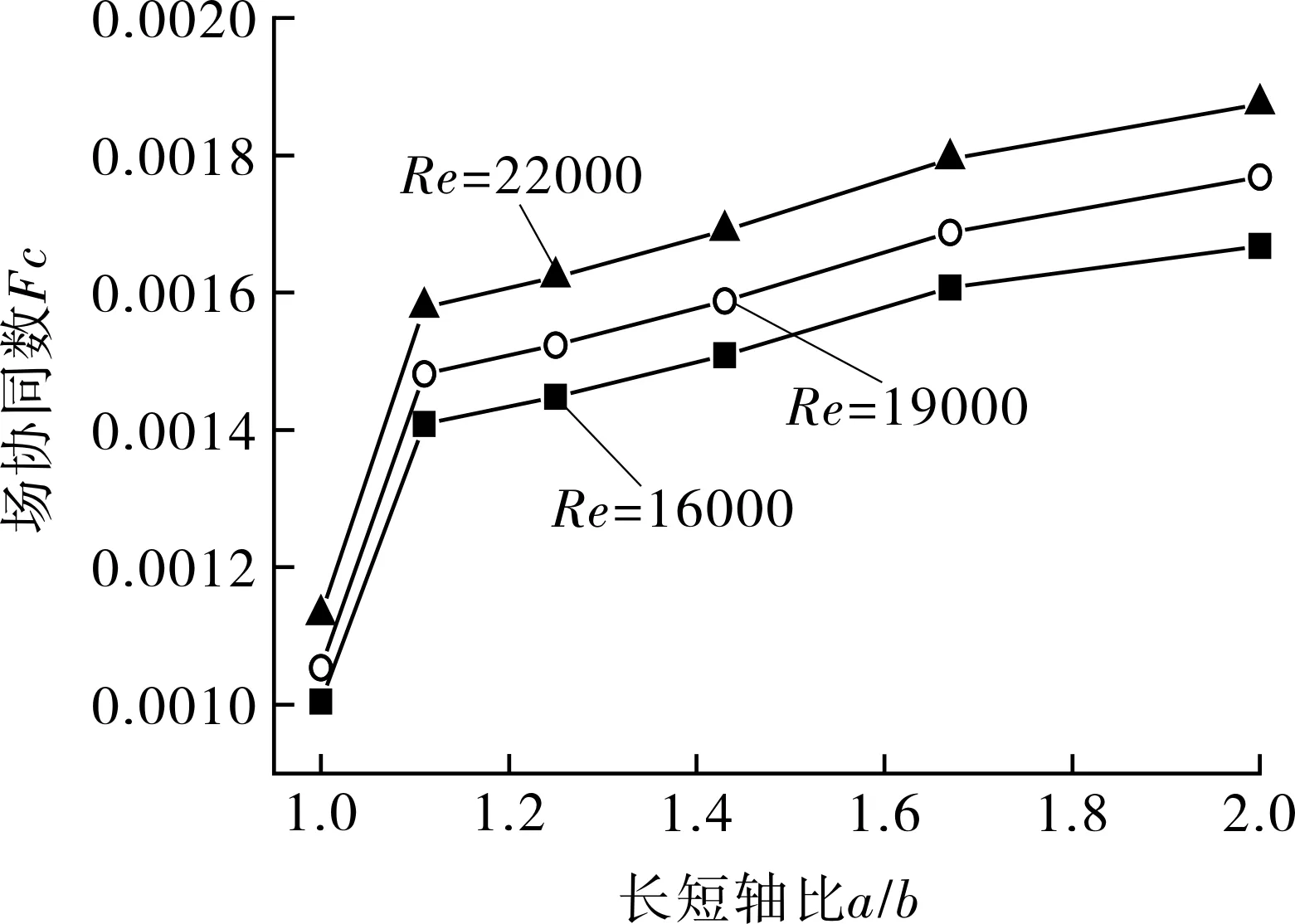
图7 椭圆管场协同数Fc对比Fig.7 Comparison of field synergy number Fc of elliptic tube

场协同数Fc表示速度场和温度梯度场的协同程度,场协同数越接近1，协同程度越好，换热能力越强。在本节的计算条件下,利用式(10)计算不同长短轴比椭圆缩放管的场协同数,场协同数对比见图7。在本文研究范围内，场协同数随着长短轴比的增加而增加，当长短轴比为2时，协同程度最高。椭圆缩放管的场协同数均大于圆管(a/b=1)。

4.2 缩放管内场协同角分布及温度变化

场协同角是温度梯度与速度之间的夹角。在0°～90°范围内，场协同角越小，协同程度越高，换热效果越好。长短轴比的增加，能够减小速度矢量和温度梯度矢量之间的夹角，从而提高协同程度。场协同角计算式[3]为：

(11)

在本节的条件下,利用式(11)计算长短轴比为2、扩缩比为3∶1,Re=16 000的缩放管场协同角，如图8所示。可以看出，缩放管的轴心以及渐缩段的场协同角较小，这是因为椭圆缩放管通过改变流体流动方向，温度梯度和速度的夹角减小，因此场协同角降低。在渐缩段中，场协同角沿径向方向先增大、后减小，这是因为渐缩段使接近壁面处的速度方向指向主流方向，流体的速度增大，同时，该处的温度梯度也有所增加，换热效果加强。渐缩段处的场协同角明显小于渐扩段，增大渐缩段的长度能够有效提升换热能力。

图8 椭圆缩放管场协同角Fig.8 Field synergy angle of elliptic convergent-divergent tube

以ECD5为例，当Re=16 000、长短轴比为2时，对椭圆缩放管内轴向、短轴径向温度变化进行分析。温度沿管长方向逐渐升高，在短轴径向上，越靠近壁面，温度增长速率越大。短轴长度在6～6.11 mm范围内温度梯度最大，温度增加了约50 ℃。温度变化情况如图9所示。随着流体的流动，热量通过壁面传递到流体中，温度上升；随着换热的进行，出口流体径向温差进一步减小，轴向温度增长速率降低。

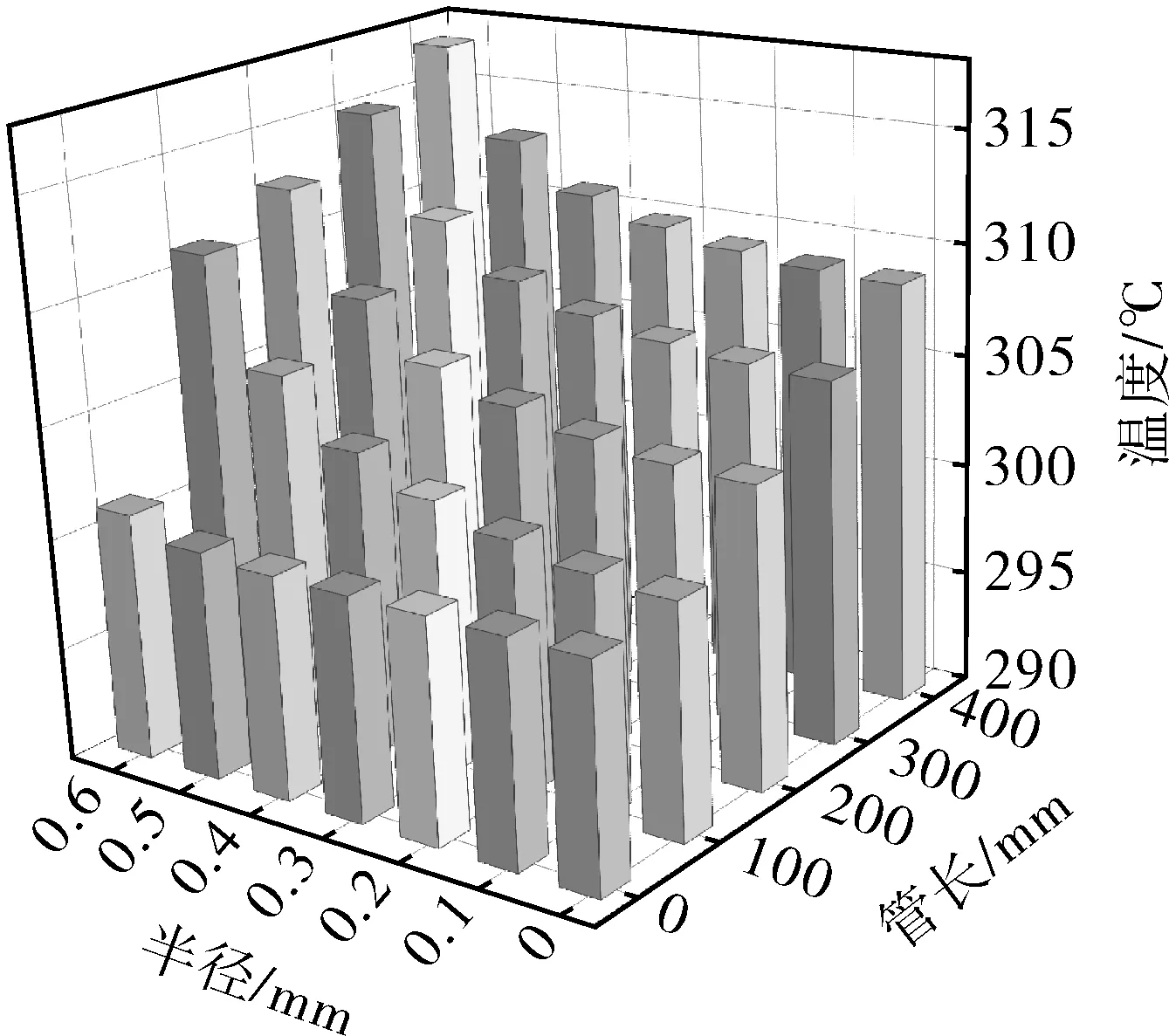
图9 椭圆缩放管内温度变化Fig.9 Temperature distribution in ellipticconvergent-divergent tubes

4.3 扩缩比及雷诺数对综合换热性能的影响

以水为管内介质，Tw=373.15 K，雷诺数Re在12 000～22 000范围内、温度为300 K的条件下，对长短轴比为2的4种不同扩缩比管型进行数值模拟,以努塞尔数和阻力系数为评价指标进行传热和流动性能分析。阻力系数计算式[23]为：

(12)

雷诺数在12 000～22 000范围内，由于雷诺数的增加使流体扰动增强，对流换热系数增加。努塞尔数随着雷诺数的增加而增加，并且增长速率基本不变。缩放节长度相等时，扩缩比越小，努塞尔数越大。ECD4管比ECD1管努塞尔数平均提高约10.8%。渐缩段使流体的速度增大，既能够加强对壁面的冲刷、减薄边界层厚度；又能增加流体的扰动，增强换热。因此，渐缩段长度越长，换热性能越好。不同扩缩比下雷诺数Re与努塞尔数Nu关系对比如图10所示。

阻力系数随着努塞尔数的增加而逐渐降低，并且降低幅度越来越小。缩放节长度相等时，扩缩比越小、阻力系数越大。ECD1管的阻力系数最小，比ECD2,ECD3,ECD4管分别平均降低为7.55%,16.7%,29.9%。不同扩缩比下雷诺数Re与阻力系数f的关系对比见图11。随着雷诺数的增加,流体冲刷壁面作用越来越大，因而边界层厚度越来越薄，流速对阻力系数的影响越来越小。

评价换热管换热效率的高低要同时考虑表面传热系数及压降。采用文献[24]中综合换热系数j作为评价指标,分析缩放管的换热能力，其计算式为：

(13)

式中,Nu0,f0为等周长圆管的努塞尔数和阻力系数。

图10 不同扩缩比下Re与Nu关系对比Fig.10 Comparison of the relationship between Re and Nuunder different divergent segment-convergent segment ratios

图11 不同扩缩比下Re与f关系对比Fig.11 Comparison of the relationship between Re and funder different divergent segment-convergent segment ratios

不同扩缩比下雷诺数Re与综合换热系数j的对比关系如图12所示。

计算结果表明，椭圆缩放管的综合换热能力与雷诺数的关系密切。随着雷诺数的增大，缩放管的综合换热能力存在一个临界点，雷诺数在12 000～16 000范围内，ECD3的综合换热能力最优；但是，当雷诺数在16 000～22 000时，ECD1的综合换热系数反而最高。这是因为渐缩段能够增强换热，但是阻力系数降低速率低于等周长圆管，扩缩比越大，降低速率越慢，因此，随着雷诺数的增加，综合换热系数反而随着扩缩比的增加而降低。

图12 不同扩缩比下Re与j关系对比Fig.12 Comparison of the relationship between Re and junder different divergent segment-convergent segment ratios

5 结论

在雷诺数为12 000～22 000范围内，长短轴比为1.11～2，以水为管内介质，通过改变扩缩比对椭圆缩放管进行了数值模拟，分析不同结构参数对其传热与流动阻力的影响，得到以下主要结论。

(1)对于等扩缩比的椭圆缩放管，场协同数随长短轴比的增大而增大。在研究范围内，长短轴比为2时，速度场和热流场的协同效果最好。

(2)对于等长短轴比的椭圆缩放管，努塞尔数随着雷诺数的增加而增加，增长速率约为0.82%。扩缩比为1∶5时的努塞尔数和阻力系数最大，即增大渐缩段的长度能够强化换热，但是阻力也会增大。

(3)在研究范围内，雷诺数为12 000～16 000、长短轴比为2、扩缩比为1∶3时的椭圆缩放管的综合换热系数最大，综合换热性能最优；当雷诺数超过16 000、扩缩比为1∶1时的综合换热性能最优。