基于非弹性分析方法的核电高温结构完整性评价框架及应用

高付海，宫建国，轩福贞

(1.华东理工大学 承压系统与安全教育部重点实验室，上海 200237；2.华东理工大学 核电装备工程研究中心，上海 200237；3.中国原子能科学研究院，北京 102413)

0 引言

2002年，第四代核能系统国际论坛通过筛选近百种核电堆型，确定了第四代核电重点发展的六种堆型[1]。自此，第四代核电技术受到世界各主要经济体国家的广泛关注，纷纷致力于相关堆型的技术研发与工程应用。国内也在布局钠冷快堆、高温气冷堆等新一代核电堆型的技术研发，稳步推进相关核电堆型的工程示范或商用电站建造[2-3]。

不同于传统的压水堆，新一代核电系统面临着更高的服役温度以及更为苛刻的启停、瞬态工况[4-5]。由此导致一系列新的与时间相关的损伤模式(如蠕变断裂、蠕变-疲劳等)的出现，成为核电装备高温结构完整性评价领域面临的突出问题[6-8]。以钠冷快堆为例，该核电系统关键装备的损伤模式如图1[1]所示，可以看出，蠕变-疲劳等损伤模式是高温核电装备结构强度分析需要重点关注的内容。

现有国际设计规范(如ASME规范[9]、RCC-MRx[10]等)均提供了针对蠕变-疲劳损伤模式的高温结构强度分析方法。在这些方法体系中，一般基于简化的弹性分析方法开展高温结构的蠕变-疲劳强度评价。在安全裕量较大、瞬态热载荷不显著等情况下，弹性分析方法是高温结构强度分析的首要选择且一般可以满足限制要求。但对于热载荷比较突出的部件或局部结构(如快堆蒸汽发生器上下腔室等)，弹性分析方法所得结果过于保守，难以充分反映结构的实际承载能力。尽管现有规范中提供了可替代弹性分析方法的非弹性分析方法基本框架，但在高温结构强度分析的具体执行层面还存在一些技术难点。因此，亟待在现有规范体系下，以蠕变-疲劳损伤模式为突破点，开发基于非弹性分析方法的高温结构强度分析方法体系及其配套工具研究。考虑到ASME规范在国内核电工程领域具有非常广泛的应用基础，故文中研究主要围绕ASME规范展开，本文以蠕变-疲劳损伤模式为例，开展非弹性分析方法及其在核电结构完整性评价中的应用研究。

1 高温结构完整性评价原理

尽管高温结构的损伤模式多样化、复杂化，但遵循如下结构完整性评价基本原理(见图2)，即工作/设计条件下的结构响应与许用临界强度的相互关系，前者为驱动力，后者为抗力。如果工作/设计条件下的结构响应小于许用临界强度，则该部件满足强度要求；反之，不满足强度要求。

工作/设计条件下的结构响应(应力、应变等)为结构强相关参量，取决于合理的本构模型(蠕变、疲劳、蠕变-疲劳等)、多轴应力处理等因素。可以通过修正弹性分析计算结果估算材料的非线性行为；也可以直接采用非线性本构模型计算结构响应。当结构的应力应变响应确定后，还需计算特定损伤模式下的强度或损伤表征参量，以最终评估结构强度是否满足要求。

许用的临界强度为材料强相关参量，依赖于材料的损伤容限、强度、安全因子等参量。其中，损伤容限一般指蠕变和疲劳损伤模式下的许用损伤限值，当同时存在两种损伤模式时，会发生明显的蠕变-疲劳损伤交互作用，导致材料损伤限值降低；材料强度指外力作用下，材料抵抗永久变形和断裂的能力；安全因子取决于材料和结构的制造技术(数据的分散性)、在役检验和监控技术等因素。

以ASME规范中蠕变强度评价(A级工况)为例，其评价方法如式(1)～(3)所示。

一次总体薄膜应力强度，限定如下：

Pm≤Smt

(1)

式中，Smt为A和B工况使用载荷下总体一次薄膜应力强度的许用值。

一次局部薄膜与一次弯曲应力强度之和，限定如下：

(2)

式中，Sm为与时间无关的应力强度限值;K为截面系数。

(3)

式中，St为与温度和时间有关的应力强度限值;Kt为考虑蠕变效应引起的外层纤维弯曲应力的减小程度,Kt=(K+1)/2。

结构响应相关参量为Pm,PL+Pb,K,Kt。前两者的确定遵循如下逻辑：首先，采用线弹性本构方程，计算结构的应力分布；然后，采用应力线性化方法，得到关键路径的薄膜与弯曲应力分量，这一过程考虑了目标区域/路径上的不均匀应力分布。参量K为截面系数，是理想弹塑性与线弹性条件下所分析截面梁模型所承载最大弯矩的比值。参量Kt为所分析截面梁模型蠕变后的应力与蠕变初始时刻应力的比值，该值的确定方法体现了通过修正弹性分析计算结果估算材料非线性行为的思想。许用的临界强度则包括Smt,Sm与St，3个参量的确定，均需要特定的材料强度并考虑相应的安全系数，如表1所示，Smt是Sm与St的较小值，故该表不再列出。

表1 临界强度Sm与St的相关参量与安全系数Tab.1 Correlation parameters of critical strength andSm and St and safety factor

2 蠕变-疲劳评价的非弹性分析方法及面临问题

本部分主要介绍ASME规范中基于非弹性分析的高温结构蠕变-疲劳强度评价方法。具体可以细分为疲劳损伤计算与蠕变损伤计算，最后根据蠕变-疲劳损伤交互作用图，判断结构的蠕变-疲劳强度是否满足要求。在此基础上，指出实施基于非弹性分析方法的高温结构蠕变-疲劳评价所面临的主要问题。

2.1 蠕变-疲劳强度分析方法

ASME规范采用寿命分数法评估高温结构蠕变-疲劳强度[9]：

∑n/Nd+∑Δt/Td≤D

(4)

式中，n为疲劳循环周次；Nd为许用疲劳循环周次；Δt为蠕变持续时间；Td为参考点许用保载时间；D为总蠕变-疲劳损伤。

该不等式左侧是蠕变损伤与疲劳损伤，不等式右侧是蠕变-疲劳强度限值。

2.1.1 蠕变-疲劳损伤计算

ASME规范中，首先分别计算高温结构的疲劳损伤和蠕变损伤，然后将两者求和即为该部件的总蠕变-疲劳损伤。

疲劳损伤的计算，需要首先确定最大应变范围。该过程需要明确循环周期中的最大与最小应变响应所对应的时刻，进而根据相应的应变分量，确定最大应变范围，如下式：

(5)

其中：

Δεxi=εxi-εxo;Δεyi=εyi-εyo
Δεzi=εzi-εzo;Δγxyi=γxyi-Δγxyo
Δγyzi=γyzi-γyzo;Δγzxi=γzxi-γzxo

式中，υ*为泊松比，非弹性分析时取0.5；o为循环中的极限条件，既可以是最大值也可以是最小值；i为循环中各个时间点；Δεxi，Δεyi，Δεzi，Δγxyi，Δγyzi，Δγzxi为时间点i与时间点o对应的应变分量差值；εxi，εyi，εzi，γxyi，γyzi，γzxi为时间点i对应的应变分量；εxo，εyo，εzo，γxyo，γyzo，γzxo为时间点o对应的应变分量。。

当最大应变范围确定后，即可通过查取对应材料疲劳设计曲线确定许用疲劳失效周次，进而实现疲劳损伤的计算。

蠕变损伤的计算，需要首先确定有效应力，其定义为等效应力与多轴应力修正项的乘积，如式(6)～(9)所示。多轴应力修正项来源于HUDDLESTON[11]的工作，考虑了多轴应力对蠕变断裂寿命的影响。

(6)

J1=σ1+σ2+σ3

(7)

(8)

(9)

式中，σi(i=1,2,3)为主应力。

C定义如下：(1)对于304SS和316SS材料，C=0.24；(2) 对于800H合金，C=0；(3) 对于2.25Cr-1Mo钢和9Cr-1Mo-V钢，①当J1/SS≥1时，C=0.16；②当J1/SS<1时，C=0。当有效应力确定后，还需除以参数K′，然后再查取许用蠕变断裂寿命，进而实现对应蠕变损伤的计算，对于ASME规范中的几种高温材料，系数K′均取0.67。

2.1.2 蠕变-疲劳强度限值

ASME规范提供了不同高温材料(316SS,304SS,2.25Cr-1Mo,800H,9Cr-1Mo-V)的蠕变-疲劳强度限值，如图3所示。可以看出，该限值由两条直线组成，不同材料的蠕变-疲劳交互曲线交点不同，316SS和304SS材料蠕变-疲劳交互曲线的交点为(0.3，0.3)；2.25Cr-1Mo钢与800H合金对应的交点为(0.1，0.1)；9Cr-1Mo-V钢对应的交点为(0.1，0.01)。该蠕变-疲劳损伤交互图由CAMPBELL[12]在1971年提出，其代表了蠕变-疲劳损伤交互作用的平均趋势。实际蠕变-疲劳设计时的保守度，则分别由计算蠕变损伤所需的蠕变断裂寿命曲线以及计算疲劳损伤所需的疲劳设计曲线纳入。

对于焊缝区域，仍可以采用上述蠕变-疲劳强度限值进行蠕变-疲劳损伤评价，但是其许用疲劳失效周次与许用蠕变断裂寿命的确定方法有所改变。具体体现在：焊缝材料的许用疲劳失效周次取母材的1/2；许用蠕变断裂寿命需在母材蠕变断裂寿命基础上乘以焊缝强度减弱系数。

图3 典型高温材料的蠕变-疲劳强度限值Fig.3 Creep-fatigue interaction diagram of typicalmaterials for elevated temperatures applications

2.2 非弹性分析面临的主要问题

总的来看，现有ASME规范提供了基于非弹性分析的高温结构蠕变-疲劳强度分析框架，可为高温结构的强度分析与安全评价提供技术途径。但目前的基本框架，还缺少一些关键信息。

(1)非弹性本构模型。其是高温结构应力应变响应分析的基础。2021版ASME规范[9]中提供了多种高温材料的弹塑性、蠕变本构模型，可以用来开展高温结构的蠕变分析、蠕变-疲劳分析(基于分离型本构)，但对于循环塑性本构、统一型蠕变-疲劳本构模型等内容，该规范尚未提供明确的本构模型。

(2)高温结构强度评价后处理软件。ASME规范中蠕变-疲劳评价程序涉及蠕变断裂寿命计算、增量步损伤累积计算等问题，容易导致人因错误、计算结果偏差大等突出问题，因此，需要开发高温蠕变-疲劳强度评价后处理软件工具，以实现高温结构蠕变-疲劳强度评价快速、准确地实施。

3 非弹性本构模型的主要形式

3.1 蠕变本构模型

ASME Ⅲ-5(2021版)规范[9]提供了高温材料的非弹性本构模型，在之前版本中未有提供。基于上述蠕变本构模型，可以实现高温结构的蠕变响应分析，进而实现高温结构蠕变损伤评价。该规范提供了多种材料(如316SS,304SS,800H,2.25Cr-1Mo,9Cr-1Mo-V)的蠕变本构模型。下文仅介绍316SS和304SS的蠕变本构模型。需要说明，若采用ASME规范中的蠕变本构模型与材料参数，应当首先验算基于蠕变本构所得结果与等时应力应变曲线中蠕变应变分量的一致性。

3.1.1 316SS材料

316SS材料的蠕变本构模型研究可以追溯到GAROFALO等[13-14]的工作，该研究表明，当温度大于700 ℃时，316钢和304钢蠕变第1和第2阶段中应变与时间的关系可由下式描述：

(10)

式中，εt为第1阶段蠕变应变的极限量；r为与第1阶段蠕变相关的常数。

EVANS等[15]的研究表明，上述方程在描述316和304钢蠕变第1阶段最初10%～15%寿命期间存在偏差。为准确表征蠕变第1阶段的贡献，引入了应变附加项，如式(11)～(20)所示。该方程即为ASME规范中316SS材料的蠕变本构模型。ASME早期相关出版物中也曾报道类似蠕变本构模型[16]。

(11)

(12)

s=max[s1,s2]=max[0.025,s2]

(13)

(14)

β=-4.257×10-4+7.733×10-7(T+273.15)

(15)

(16)

r=max(r1,r2)

(17)

r1=L(145.037681σ)n-3.6

(18)

(19)

(20)

式中，G,H,D,n,Q,R,C,L,B,A为材料参数。

3.1.2 304SS材料

304SS材料的蠕变本构模型发展历程与316SS材料类似，此处不再赘述。该材料的蠕变本构模型如式(21)～(28)所示。

(21)

(22)

(23)

βr=-2.252×10-4+5.401×10-7(T+273.15)

(24)

(25)

(26)

(27)

βe=-3.652×10-4+7.518×10-7(T+273.15)

(28)

式中，nr，ne为材料参数。

3.2 疲劳本构模型

ASME规范中没有提供材料的疲劳本构模型，但RCC-MRx规范[10]中提供了适用于高温结构疲劳分析的本构模型，简要介绍如下。

当材料的粘性行为可忽略时，可以采用弹塑性分析开展工程结构的疲劳分析。该规范提供了四大类本构模型：理想弹塑性、各向同性应变硬化(双线性、多线性、非线性硬化)、随动硬化(双线性、多线性、非线性硬化)、组合硬化(包括Chaboche,Burlet-Cailletaud,Guionnet,Chaboche-Ohno-Wang弹塑性本构模型)。在解决工程结构疲劳分析时，尤以组合硬化模型较为合理且为规范所推荐。以Chaboche组合硬化模型为例，其本构模型如下。

屈服准则：

(29)

式中，σy为初始屈服强度。

塑性流动准则：

(30)

式中，dλ为塑性乘子。

非线性随动硬化法则：

(31)

各向同性应变硬化法则：

(32)

应变记忆效应：

Q(q)=QM-(QM-Q0)exp(-2βq)

(33)

式中，a,c,b,QM,Q0,β为材料常数。

当材料的粘性行为不可忽略时，需要采用统一型粘塑性本构模型开展工程结构的疲劳分析。最为经典的当属Chaboche模型，与弹塑性模型不同的是，塑性流动法应由以下粘塑性流动法则代替：

(34)

式中，K，n为材料常数。

在快堆等先进核电高温结构疲劳分析中，已有统一型粘塑性本构模型在工程疲劳问题中应用的报道[17-19]。这些本构模型多为RCC-MRx体系中Chaboche统一型粘塑性模型或其改进形式。当然也有部分研究开展基于Ohno-Wang统一型粘塑性本构模型[20-21]的模型适用性验证等工作[22]。

3.3 蠕变-疲劳本构模型

蠕变-疲劳本构模型可以分为两大类：一类是统一型本构模型；另一类是分离型本构模型。

对于统一型粘塑性本构模型，上述Chaboche统一型粘塑性本构模型一般也可以应用到蠕变-疲劳载荷工况下。还有一些研究人员开发了改进的蠕变-疲劳本构模型[23]，但这些模型一般适用于短保载条件下的蠕变-疲劳行为描述，而长时保载条件下，材料的应力、应变显著过估，尚不能较为准确地描述长时条件下的应力松弛行为。为体现保载阶段的蠕变变形与损伤行为，已有文献报道考虑蠕变损伤的蠕变-疲劳本构模型[24]。上述本构模型在特定应用场景取得了研究进展或应用突破，但由于该类本构模型过于复杂，其适用性仍需大量验证分析。因此，统一型粘塑性本构模型在工程结构蠕变-疲劳分析问题中的应用还需要进一步研究。

图4 分离型蠕变-疲劳本构模型基本框架Fig.4 Framework of non-unified creep-fatigueconstitutive model

对于分离型粘塑性本构模型，其具有物理含义清晰，相对简单、操作方便等优点，在工程中得到了相对广泛的应用。当不考虑热变形时，可采用如图4所示的框架。可以看出，弹塑性变形行为可由理想弹塑性、应变硬化等模型进行表征；而蠕变变形行为可由蠕变本构模型描述，包括Norton-Bailey等模型。

3.4 本构模型的数值实现

当材料本构模型确定后，需要考虑本构模型的数值实现问题。在有限元分析软件Abaqus[25]框架下，可以通过编制相应的用户子程序实现本构模型与有限元软件的相互嵌入。蠕变本构模型、分离型蠕变-疲劳本构模型均可以通过用户子程序CREEP实现；疲劳本构模型、统一型蠕变-疲劳本构模型则需要通过材料子程序UMAT实现。

4 高温结构强度评价后处理

后处理涉及蠕变断裂寿命计算、蠕变-疲劳损伤计算等，过程复杂繁琐，是高温结构完整性评价需要考虑的另一关键内容。

4.1 蠕变断裂寿命计算

蠕变过程中，局部不连续区域的高应力不断松弛。若实现蠕变损伤的精准计算，需要精确计算每一个增量步对应的蠕变断裂寿命。Larson-Miller方程(见式(35))可以实现不同温度、应力水平下的蠕变断裂寿命计算，但是，当用于较宽温度范围、应力水平范围等条件下时，会导致较大的预测误差。因此，需要建立合理的蠕变断裂寿命计算策略，进而实现蠕变断裂寿命的精确确定。

f(σ)=T(C+lgtr)

(35)

可以采用如下原则实现蠕变断裂寿命的精确计算：依据目标温度所在最近的两个温度点对应数据，获得材料的Larson-Miller方程；再根据目标温度值以及应力水平，确定蠕变断裂寿命，这一过程可以通过用户子程序UVARM或USDFLD实现，也可以通过MATLAB程序实现。

4.2 蠕变-疲劳损伤评价

第3节介绍了核电高温结构蠕变-疲劳损伤评价流程。可以发现，最大应变范围的确定(用于疲劳损伤计算)，需要确定循环周期中最大值与最小值，上述过程的实现需要依赖于后处理程序，以避免大量重复手算工作。相应地，有效应力的确定(用于蠕变损伤计算)，需要确定服役周期中的总蠕变损伤，该过程的实现也需要依赖于后处理程序。上述过程可以通过用户子程序UVARM或USDFLD实现。

5 应用案例

以过热器下腔室某整锻件接管为例，开展高温结构的蠕变-疲劳强度分析与寿命评价。该部件材料为2.25Cr-1Mo钢，服役温度510 ℃、工作压力12 MPa、启停次数300次(按0→12 MPa→0不断循环)、设计寿命13.1万h。

采用有限元分析软件Abaqus开展该部件的蠕变-疲劳损伤评价。采用1/2模型进行几何建模，忽略模型上部与下部区域的影响,采用三维实体单元C3D8R进行网格划分，共生成48 220个单元和54 356个节点。

采用分离型蠕变-疲劳本构模型开展高温结构的应力应变响应分析。弹塑性本构模型可以采用ASME Ⅲ-5(2021版)提供的本构模型。对于蠕变本构模型，试算ASME Ⅲ-5(2021版)中的蠕变本构模型发现：部分温度点下，该模型的应变结果过大，与直接提取等时应力应变曲线所得蠕变应变结果差异过大。因此，本案例不再采用规范提供的蠕变本构模型，而是采用较为简单的Norton-Bailey蠕变本构模型(见式(36))。拟合材料参数用到的蠕变应变数据，从等时应力应变曲线族中提取。需要说明，在后面ASME版本更新后，仍推荐采用规范所提供的本构模型。

(36)

式中，A1,n1,m1均为材料参数。

采用蠕变用户子程序CREEP将上述本构关系嵌入到有限元分析软件中。

蠕变断裂寿命以及蠕变-疲劳损伤等关键参量计算，采用用户子程序UVARM实现。基于该子程序，可以在数值计算过程中，实时计算各增量步的损伤等数据。

由于实际循环周次较多，本例仅计算前10周次的应力应变响应以及相应损伤参量；第10周次及以后周次的相关结果参考第10周次处理。危险点处的应力/应变、应变范围演化过程如图5,6所示。可以看出，保载过程中，危险点处的应力发生显著松弛，由初始加载后的97 MPa逐渐降低到57 MPa；应变随时间的进行不断累积，但累积速度不断趋于平缓；应变范围在第1周出现最大值，后续循环周次中均未超出该值。最大应变范围分布云图如图7所示，可以看出，最大应变范围出现在筒体与接管连接区域，其中，应变范围的计算，仅考虑当前周次内的应变响应演化过程。

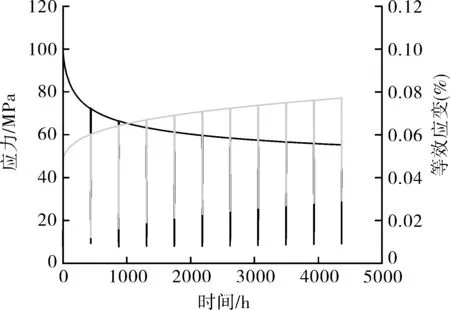
图5 危险点处应力与应变演化过程(前10周次)Fig.5 Evolution of stress and strain for point of concern(within first 10 cycles)

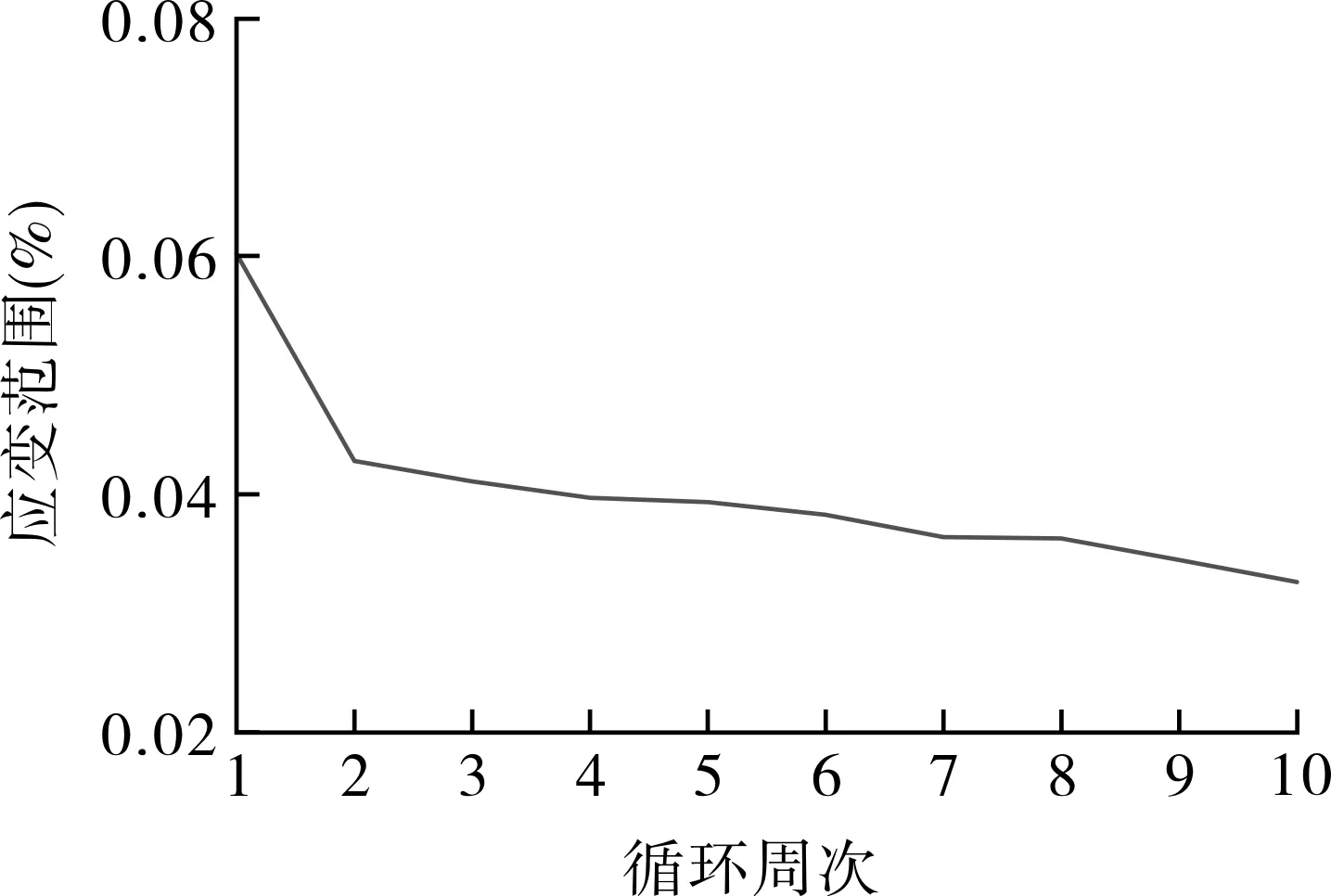
图6 危险点处应变范围演化过程(前10周次)Fig.6 Evolution of strain range for point of concern(within first 10 cycles)

图7 结构应变范围分布云图Fig.7 Distribution nephogram of strain range of the component

基于上述相关计算结果，可以评估结构的蠕变-疲劳强度。该结构的蠕变损伤(前10周次累积量)分布云图如图8所示。与应变范围分布特征类似，最大蠕变损伤集中在筒体与接管连接区域。基于第10周次的蠕变损伤确定后续循环过程中的蠕变损伤，最终得到总蠕变损伤为0.94。基于最大应变范围，可以确定结构的疲劳损伤，为0.000 3。上述蠕变损伤与疲劳损伤之和小于对应的蠕变-疲劳强度限值。这表明：现有结构满足蠕变-疲劳强度限值要求。需要说明，由于忽略了后续循环过程中的应力松弛，基于第10周次的蠕变损伤确定后续循环过程中的蠕变损伤，这一处理方法所得结果较为保守。

图8 结构蠕变损伤分布云图Fig.8 Distribution nephogram of creep damage of the component

6 结语

新一代核电高温部件面临较高服役温度、超长服役周期、复杂运行工况等苛刻条件，结构损伤模式多样化、复杂化。因此，复杂损伤模式下高温部件的力学分析与评价是先进核电结构完整性领域面临的重要课题。

传统的基于弹性分析方法的高温部件结构完整性评价所得结果保守性较大，在热应力突出等条件下保守度过大甚至难以通过，而现有ASME规范体系下的非弹性分析方法为结构强度分析与评价提供了另一选项。尽管当前国内工程界对于非弹性分析方法的应用存在疑虑和担忧，但随着分析技术的不断进步以及试验手段的补充验证，非弹性分析方法的工程应用与广泛普及并非遥不可及。

分离型本构模型具有模型形式简单、操作方便等优点，是当前核电高温结构力学分析与评价的重要手段。相对而言，统一型本构模型存在模型复杂、参数众多、长时保载结果偏差过大等一系列问题，从长远来看，该类模型仍是高温材料非弹性本构模型的发展方向。

非弹性分析方法涉及复杂本构模型，现有有限元分析软件用户界面均不支持，需要开发配套的用户子程序；同时，非弹性分析框架下，高温结构的蠕变-疲劳强度评价流程相对繁琐，涉及蠕变断裂寿命、蠕变与疲劳损伤计算等过程，需要开发相应的后处理分析软件或工具。因此，面向工程应用的非弹性本构模型及蠕变-疲劳损伤分析计算后处理程序开发是高温结构完整性评价的重要内容。