基于非接触磁特性参数的埋地管道可靠度MCMC定量评价模型

邢海燕，王松弘泽，孙晓军，段成凯，刘 传，弋 鸣，刘伟男

(1.东北石油大学 机械科学与工程学院，黑龙江大庆 163318；2.哈尔滨工程大学 动力与能源工程学院，哈尔滨 150001)

0 引言

随着我国油气资源的开发建设，根据“十三五”规划，2020年底我国油气长输管道总里程已达到16万km，但目前其中大约一半已服役超过20年，老化问题十分突出，且埋地油气长输管道运行环境复杂，一旦发生泄漏、爆炸等事故，往往造成灾难性的后果[1-2]。因此，可靠度评价对于埋地管道安全运行至关重要。但是，对于在役运行的埋地管道，进行全面开挖检测不经济、也不现实，而常用的无损检测方法在不开挖条件下对埋地管道进行可靠度评价存在困难，涡流、漏磁、超声等方法在非接触检测领域，分别存在趋肤效应、周向磁化困难、阻抗不匹配等检测障碍[3]；漏磁、超声等管道内置式检测，由于空间和角度的限制经常造成卡堵问题、检测成本非常高。

在20世纪末兴起的金属磁记忆检测技术(MMM)，既可发现宏观缺陷；又能发现因异常应力集中引起的早期损伤，在无损检测领域显示其独特优势。XU等[4]研究了不同疲劳阶段磁信号间的变化规律，得出磁性信号随位错钉扎因子的增加而增强的结论；KOLOKOLNIKOV等[5]研究了弱磁下的焊接过程中，应力变化与自磁场强度之间关系；刘斌等[6-7]根据电子自旋理论和洪德法则，基于全势线性缀加平面波法(FLAPW)建立了磁力学模型，得到屈服极限前后的磁记忆信号特征，并定量解释应力集中与自漏磁场之间的关系；HU等[8]研究了对接焊缝宏观缺陷影响因素，获得不同灵敏度方向和剥离值的磁记忆信号的特性；胥永刚等[9]提出了基于固有时间尺度分解(ITD)的磁记忆特征提取方法，研究低速重载齿轮故障的早期检测；兰清生等[10]通过研究李萨如图当量面积变化，探讨试件不同的应力集中状态；易方等[11]提出一种基于模糊核支持向量机的管道缺陷识别方法；DUBOV[12]针对冶金生产中缺陷的不确定性难题，提出一种基于MMM检测的缺陷诊断方法；杨理践等[13]基于密度泛函理论，建立铁磁晶体磁记忆模型,采用正交化平面波赝势法研究塑性变形后磁记忆信号变化特征；邢海燕等[14]利用MMM方法，建立了不同载荷下角焊缝缺陷处应力集中程度的定量表征模型。

针对不开挖条件下、在役运行的埋地管道可靠度定量评价难题，提出基于金属磁记忆检测技术的可靠度定量评价方法。为此，进行埋地管道非接触磁记忆检测试验，首先引入Kendall相关系数，分析缺陷尺寸与不同磁特性参数之间的相关性，并获取不同压力条件下ΔH(y)与d、k(x,y)与L之间的非线性回归拟合修正式；之后结合Modified B31G评价标准，利用埋地管道的多种非接触磁特性参数，在蒙特卡洛法基础上，引入能够反映管道缺陷动态时变性的马尔科夫链，建立基于非接触磁特性参数的埋地管道可靠度马尔科夫链蒙特卡洛(Markov Chain Monte Carlo,MCMC)定量评价模型。通过算法比较与现场试验，验证模型的有效性，为实际工程中的埋地管道可靠度定量评价提供一种新的方法。

1 试验方法

试验材料采用输油管道常用的L245N钢管，尺寸为∅325 mm×15 000 mm，壁厚10 mm，一端焊有盲板，另一端留有接口与液压泵连接，对管道试件施加不同等级内压：0,3,5,8,10,12,15 MPa(其中0,5,10,15 MPa为分析数据，其余为检测数据)。为研究基本条件下，不同尺寸缺陷的非接触磁特性参数表征规律，如图1所示，在第1组管件沿管长方向预制4个圆形缺陷，以模拟实际工况中常见的点蚀腐蚀，长度L均为15 mm，深度d分别为2,4,6,8 mm；在第2组管件以同样间隔预制4个缺陷，深度d均为4 mm，长度L分别为5,10,15,20 mm，每组管件数量均为6个。试验中将2组管件埋地1 m深，在地面上做好轴线标记，利用TSC-5M-32型磁记忆仪和11-6W型非接触探头组成检测系统，对不同内压下的管件沿轴线的3条测试路径进行非接触扫描检测，获取不同尺寸缺陷的非接触磁记忆信号，试验布置如图2所示。

(a)第1组管件

(b)第2组管件图1 试验用管件示意Fig.1 Schematic diagram of tubular specimen

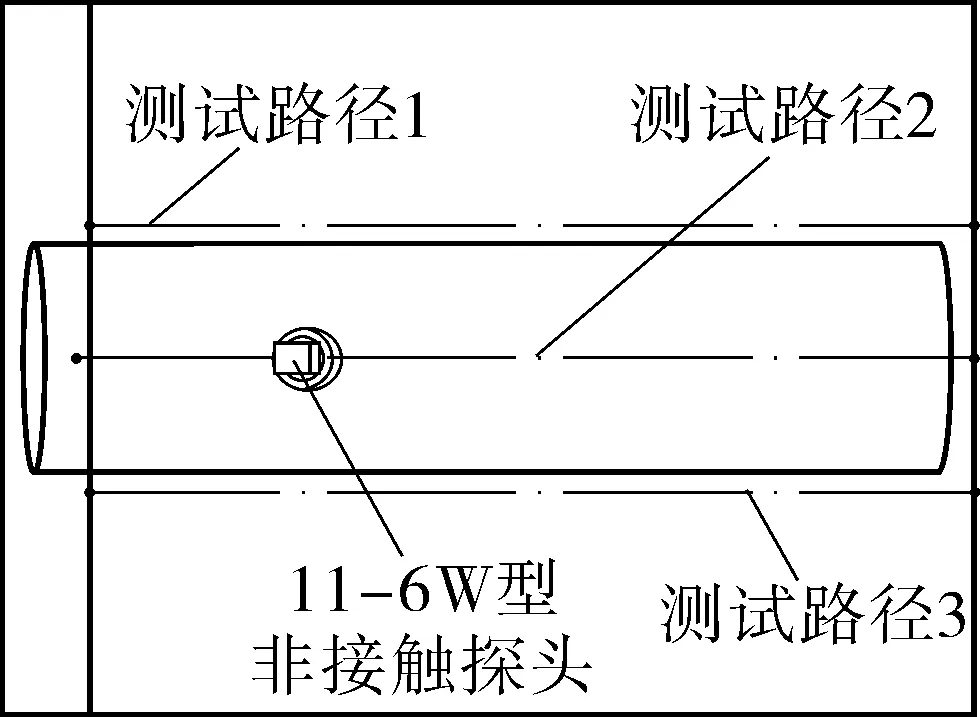
(a)测试路径布置

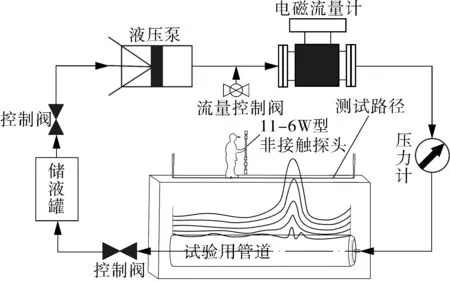
(b)试验布置图2 试验布置示意Fig.2 Schematic diagram of experimental layout

2 试验结果分析

2.1 磁特性参数提取

通过试验得到不同内压P下，所对应不同缺陷长度L和缺陷深度d的非接触磁记忆数据，提取如下磁特性参数(如图3所示)。

切向磁场强度峰峰值ΔH(x):

ΔH(x)=H(x)max-H(x)min

(1)

式中,H(x)max,H(x)min分别为切向磁记忆信号在缺陷附近区域的最大值与最小值。

法向磁场强度峰峰值ΔH(y):

ΔH(y)=H(y)max-H(y)min

(2)

式中,H(y)max,H(y)min分别为法向磁记忆信号在缺陷附近区域的最大值与最小值。

合成磁场强度峰峰值ΔH(x,y):

(3)

切向磁场强度变化率k(x):

(4)

式中,x为坐标位置；Δx1为切向磁记忆信号在缺陷附近区域取最大值与最小值时的位置坐标之差。

法向磁场强度变化率k(y):

k(y)=[H(y)max-H(y)min]/Δx2

(5)

式中,Δx2为法向磁记忆信号在缺陷附近区域取最大值与最小值时的位置坐标之差。

合成磁场强度变化率k(x,y):

(6)

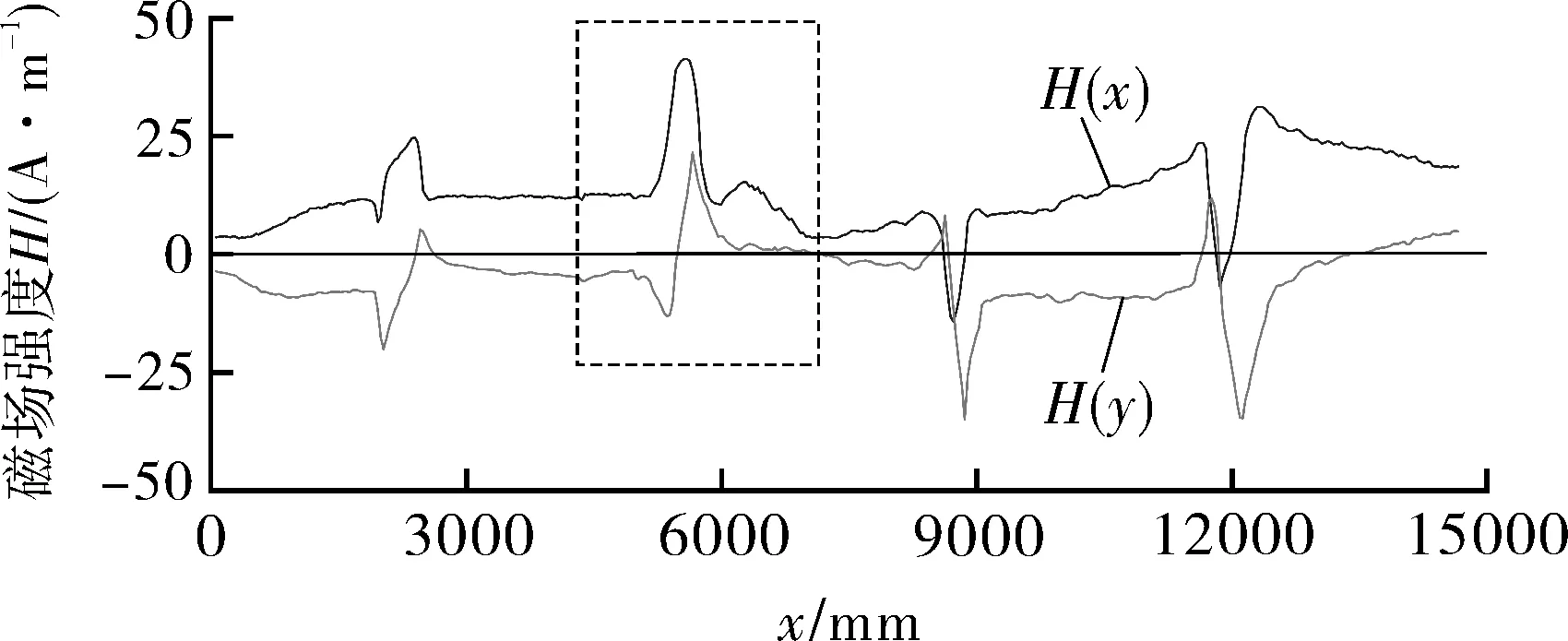
(a)原始信号

(b)特性参数提取图3 磁记忆原始信号与特性参数提取Fig.3 Extraction of magnetic original signals andcharacteristic parameters

2.2 缺陷深度与磁特性参数的关系

经试验数据分析可知，第2.1节中各磁特性参数与缺陷深度d、缺陷长度L对应关系的相关程度存在差异。为此，在数据总体分布未知情况下，引入Kendall相关系数[15]，对不同缺陷深度和长度磁特性参数的相关性进行研究。

首先，由试验获取0 MPa内压、缺陷长度L=15 mm、缺陷深度分别为d=2,4,6,8 mm对应的ΔH(x),ΔH(y),ΔH(x,y),k(x),k(y)，k(x,y)数值，通过统计产品与服务解决方案软件(Statistical product and service solutions，SPSS)计算得到不同缺陷深度d的Kendall相关系数值；其次，按上述方法继续施加不同等级内压P=5,10,15 MPa，完成不同内压下各磁特性参数Kendall系数值的计算。以压力P为横坐标，Kendall值为纵坐标，得到不同内压下各磁特性参数的Kendall相关系数，如图4所示。由图4可知，缺陷长度L一定，随压力P和缺陷深度d的改变，相对于其他磁特性参数，唯有法向磁场强度峰峰值ΔH(y)在各压力等级下与d相关系数均接近1，证明ΔH(y)可敏感反映并表征d的变化规律。在此基础上，给出ΔH(y)与d之间的对应关系，如图5所示。

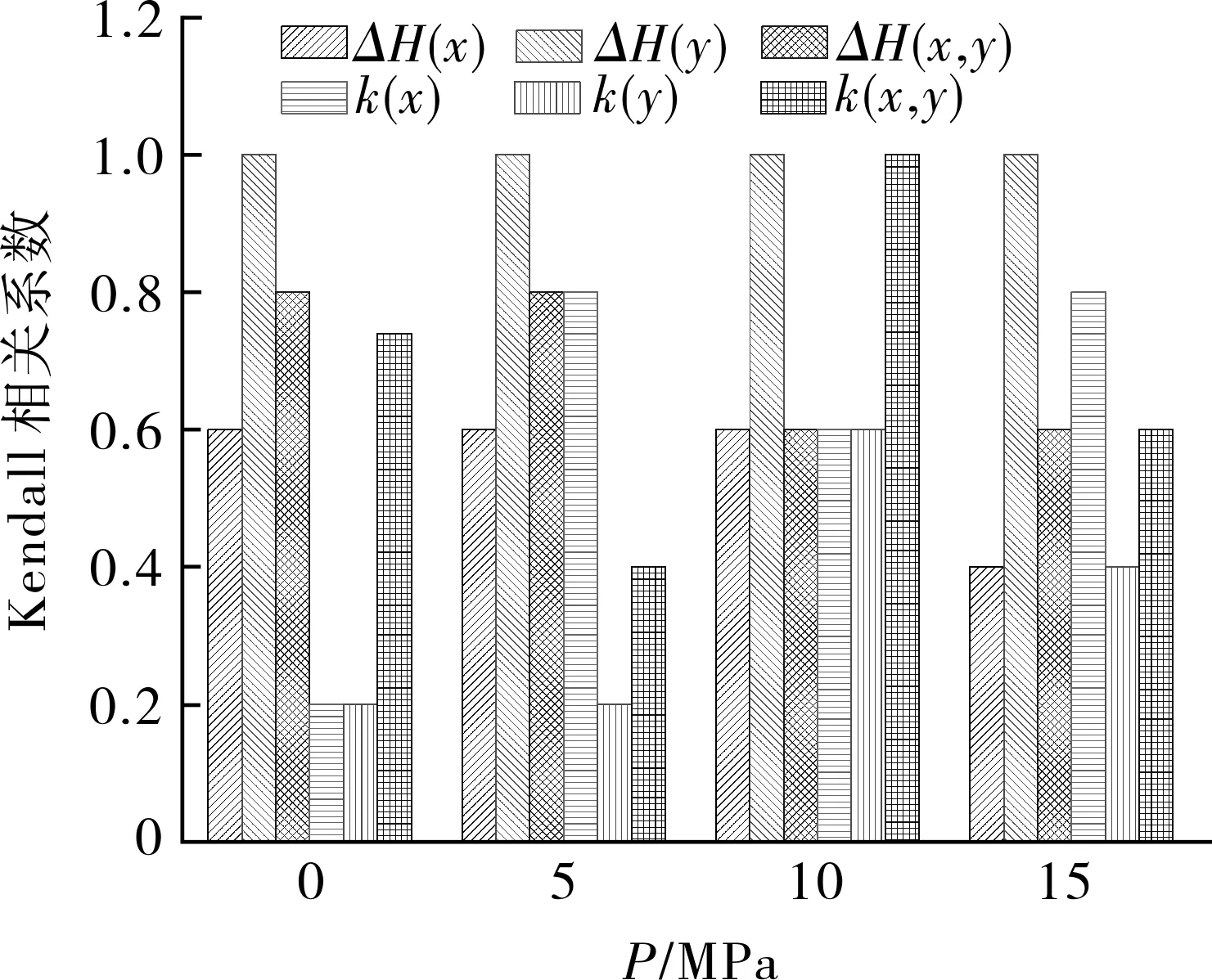
图4 不同内压下各磁特性参数Kendall相关系数Fig.4 Kendall correlation coefficient of each magneticcharacteristic parameter at different internal pressures

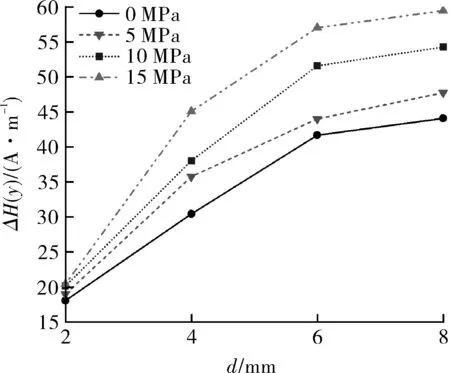
图5 ΔH(y)与d的试验数据关系曲线Fig.5 Curves of experimental data for ΔH(y)-d correlation

对图5的ΔH(y)与d关系曲线进行非线性回归拟合，可得：

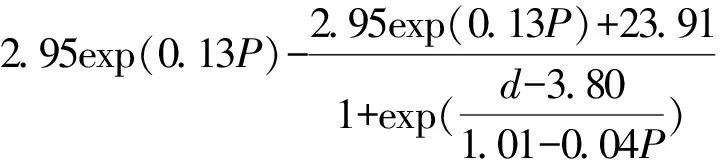
+40.89

(7)

考虑ΔH(y)公式值与实际值间存在误差，引入系数λ,μ分别对P和d进行修正，如下式：

ΔH(y,λ,μ)=2.95exp(0.13λP)-[2.95

×exp(0.13λP)+23.91]/[1

(8)

为保证获取最优的修正系数λ,μ，将图5中数据点所对应的d,P，ΔH(y)值与式(8)相结合，获取一系列修正系数λ,μ。根据每组λ,μ所对应式(8)中ΔH(y)计算值与试验值间的相对误差，绘制不同修正系数λ,μ与相对误差的三维图，见图6。可以看出，相对误差先减小、后增大，即存在相对误差极小值，优选最小相对误差对应的修正系数：λ=0.97,μ=0.95。

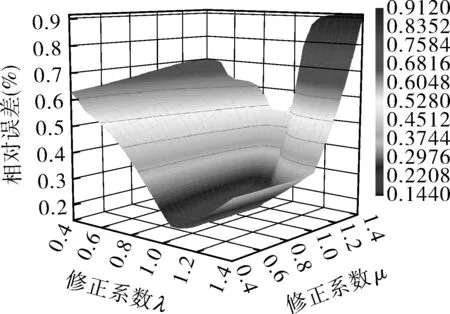
图6 不同修正系数对应的相对误差三维图Fig.6 3D diagram of relative errors for differentcorrection coefficients

将试验中3,8,12 MPa压力下的ΔH(y)值用于修正公式的验证，结果如图7所示。分析得出，同一压力和缺陷深度条件下，ΔH(y)实测值与公式值的误差最大为6.07%，说明修正公式有效。

图7 ΔH(y)实测值与预测值对比Fig.7 Comparison between measured and predictedvalues of ΔH(y)

2.3 缺陷长度与磁特性参数的关系

引入Kendall相关系数，按上述方法完成对试验所获各磁特性参数与缺陷长度L之间相关性的定量研究，获取不同内压下各磁特性参数的Kendall相关系数，结果见图8。可以看出，缺陷深度d一定，随压力P和缺陷长度L的改变，相对于其他磁特性参数，合成磁场强度变化率k(x,y)在各压力等级下与L相关系数均接近1，证明k(x,y)可敏感性反映并表征L的变化规律。进一步给出了k(x,y)与L之间的对应关系，如图9所示。

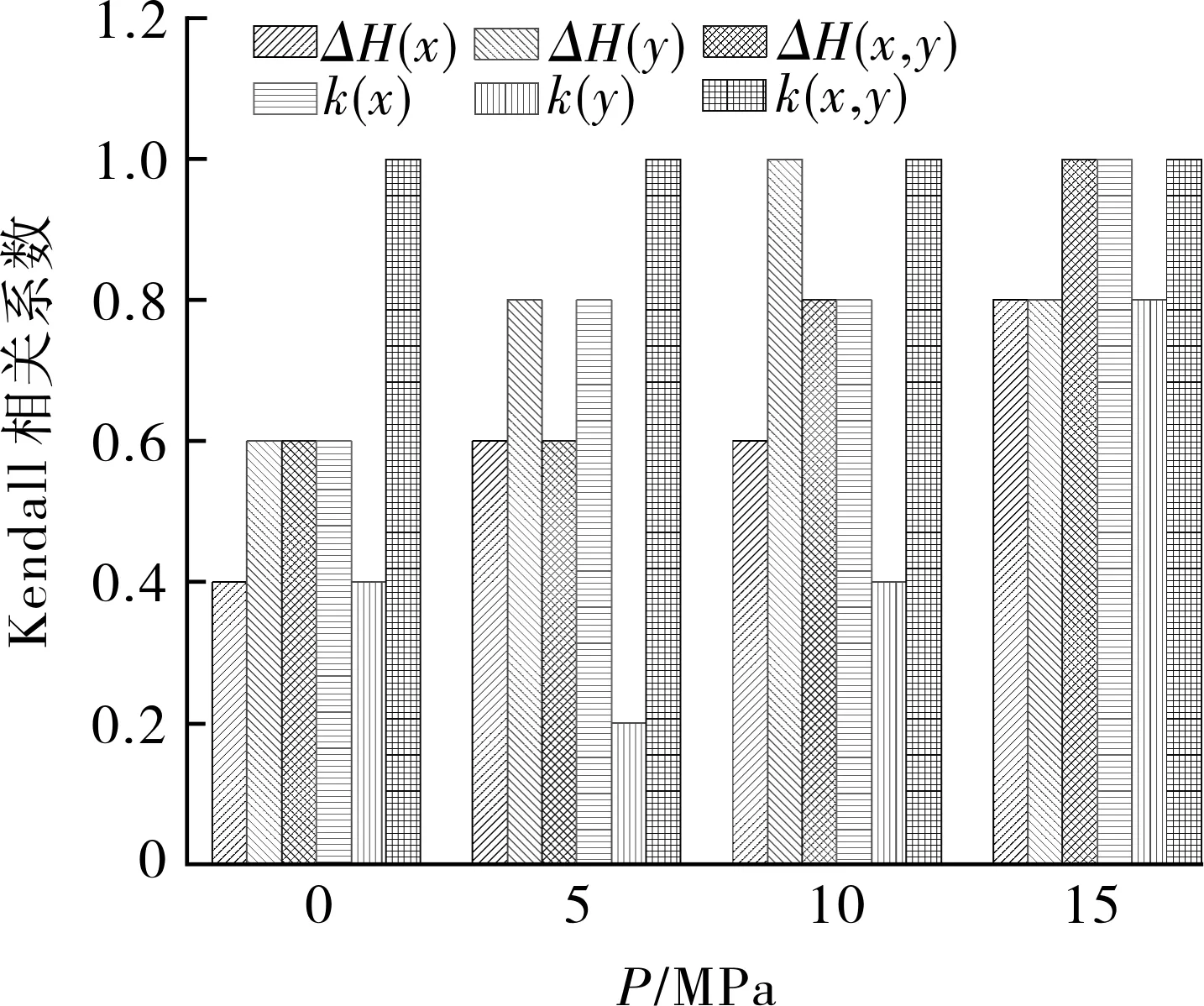
图8 缺陷长度Kendall相关系数Fig.8 Kendall correlation coefficient of defect length

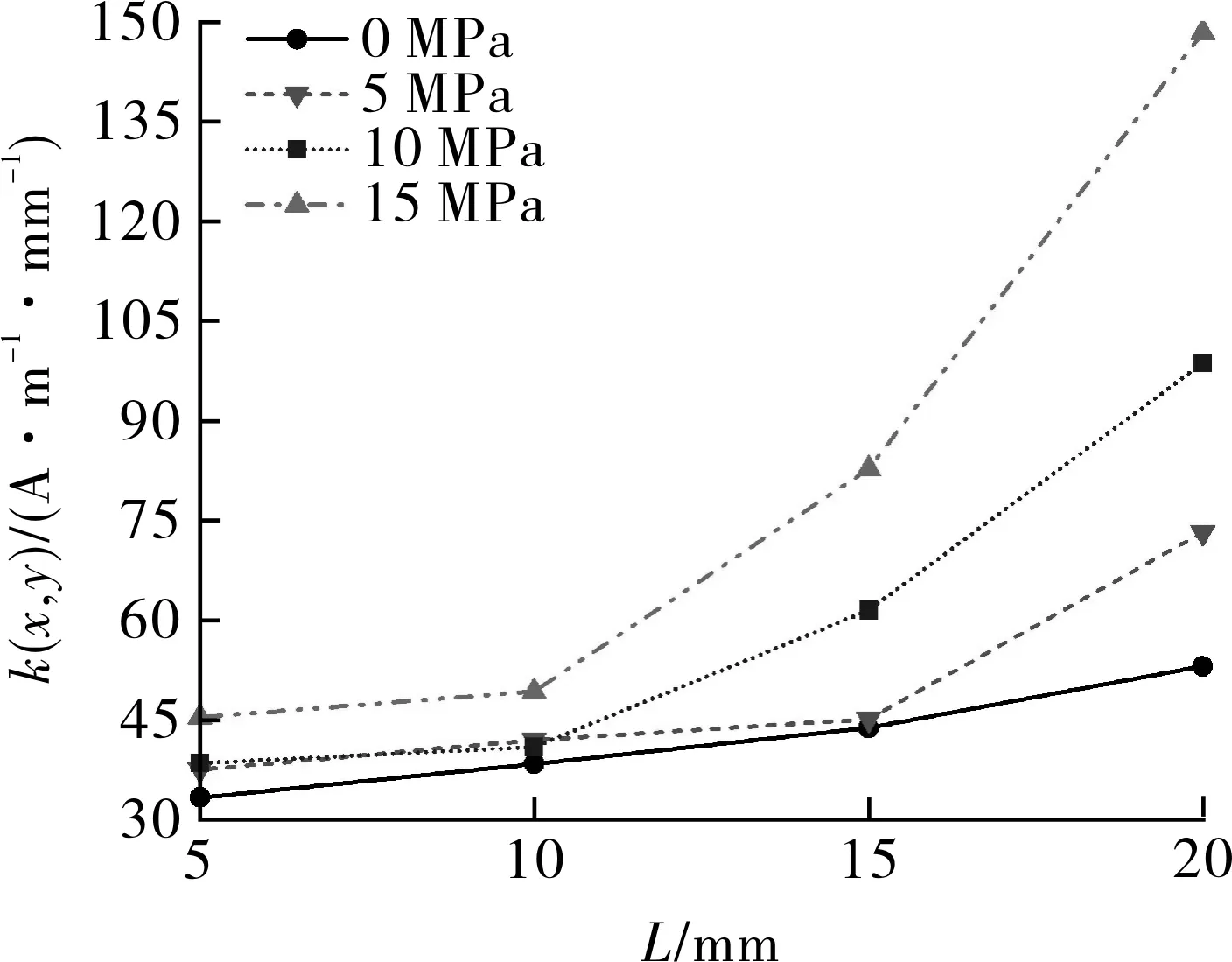
图9 k(x,y)与L的试验数据关系曲线Fig.9 Curves of experimental data for k(x,y)-L correlation

对图9所示的k(x,y)与L关系曲线进行非线性回归拟合，同样考虑k(x,y)公式值与实际值间存在误差，引入系数α,β分别对P和L进行修正，如下式：

k[(x,y),α,β]=[0.30exp(0.16αP)+2.21]

(9)

为了保证最优修正系数α,β，采用第2.2节的相同方法，绘制不同组α,β下对应的相对误差三维图，如图10所示，可以看出，相对误差先减小、后增大，存在误差的极小值，优选修正系数：α= 1.04,β= 0.98。

将试验中3,8,12 MPa压力下的k(x,y)值用于修正公式的验证，结果如图11所示。分析得出，同一压力和缺陷长度条件下k(x,y)的实测值与公式值的误差最大为8.79%，修正公式有效。

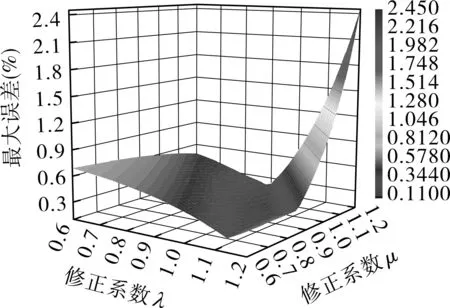
图10 不同修正系数对应的相对误差三维图Fig.10 3D diagram of relative errors for differentcorrection coefficients

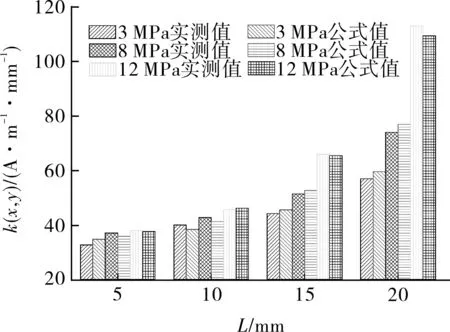
图11 k(x,y)实测值与预测值对比Fig.11 Comparison between measured andpredicted values of k(x,y)

3 基于非接触磁特性参数的埋地管道可靠度MCMC模型建立

3.1 磁特性参数分布

由上述得知，缺陷深度d和缺陷长度L为影响管道失效的关键性因素。为建立基于磁特性参数的可靠度模型，将两组管件240组ΔH(y)实测数据进行统计分析，得到统计结果如图12所示。

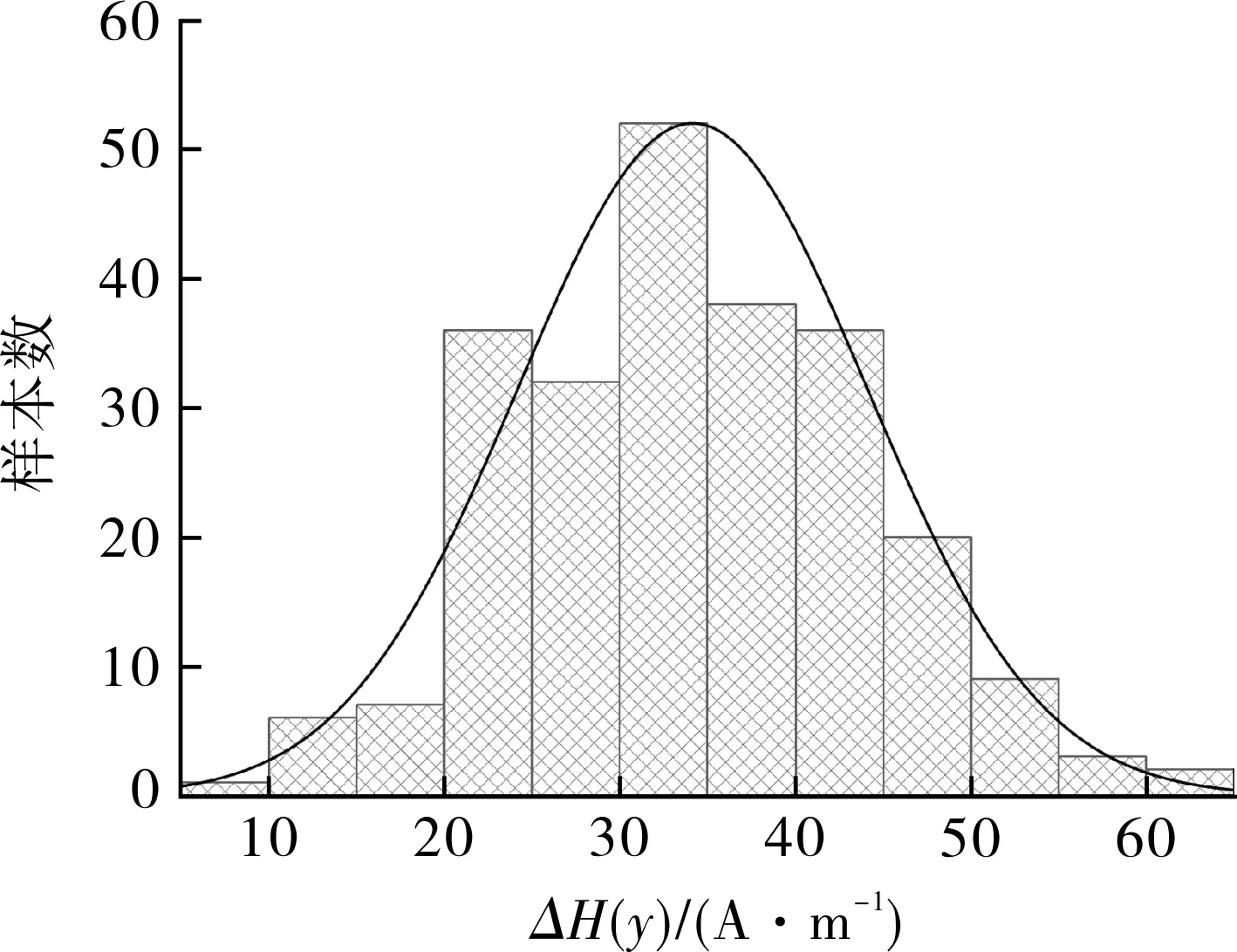
图12 ΔH(y)统计分布图Fig.12 Statistical distribution of ΔH(y)

同理，将两组管件240组k(x,y)实测数据进行统计分析，得到统计结果如图13所示。可以看出ΔH(y)符合正态分布、k(x,y)符合对数正态分布，可以基于上述磁特性参数建立埋地管道的可靠性模型。

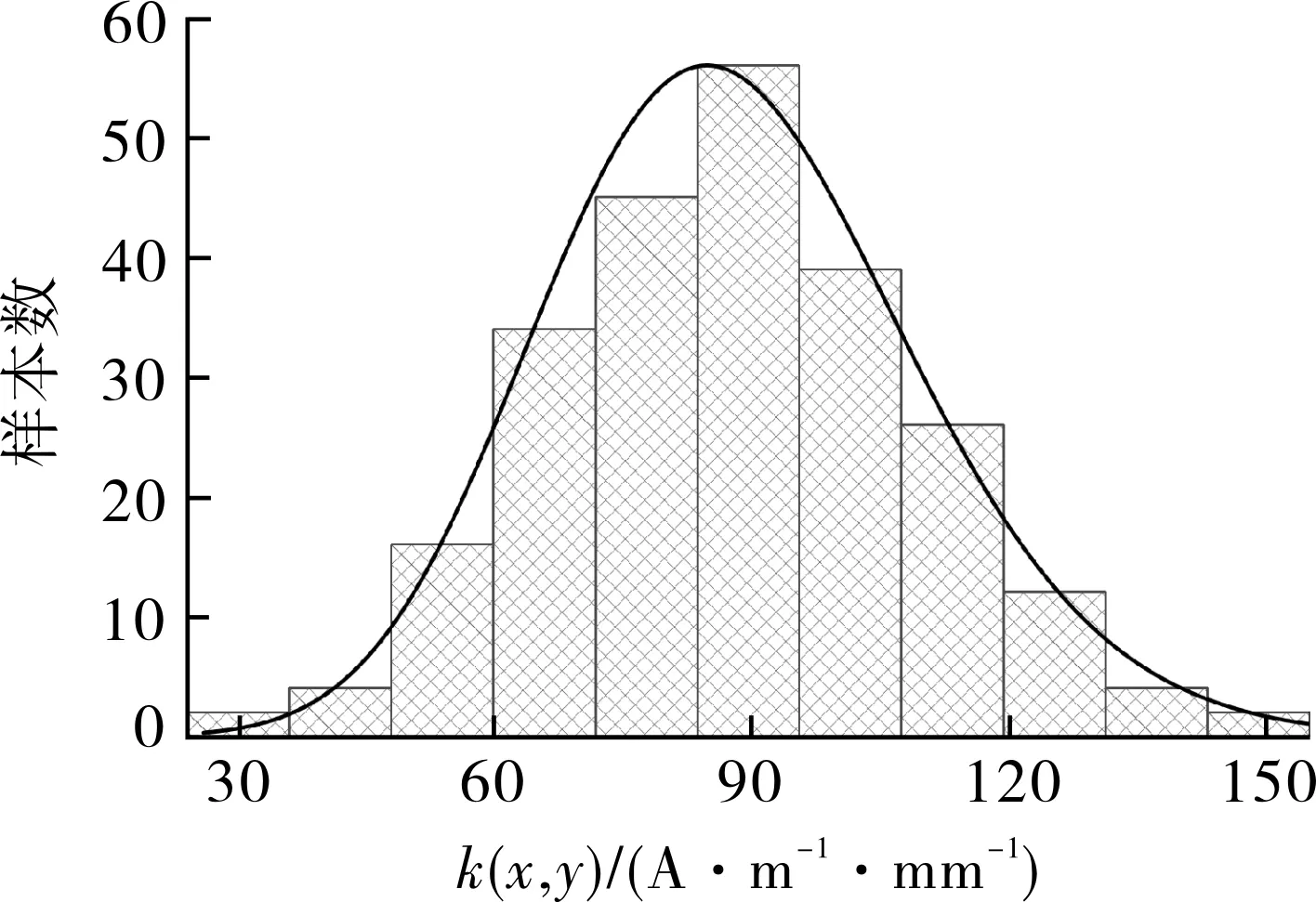
图13 k(x,y)统计分布图Fig.13 Statistical distribution of k(x,y)

3.2 可靠度定量模型建立

对于油气长输管线来说，其破损通常与管道的失效应力r、实际应力s直接相关，将r和s看成随机变量，则描述管道失效的极限状态函数Z为：

Z=r-s

(10)

若Z>0，则管道失效应力r大于实际应力s，管道可靠；反之，则管道将损坏。

在油气管道评价中，国际上广泛采用的Modified B31G准则有着高可靠度与低误差的特性[16]。为使所建可靠性模型具有实际应用价值，引入该准则：

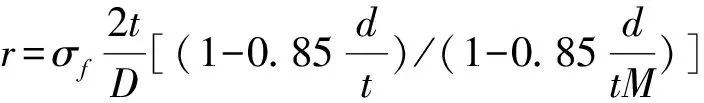
(11)

式中，r为环向失效应力,MPa;σf为流变应力,MPa,σf=1.1σs(σs为屈服应力);t为管道公称壁厚,mm;D为管道外径,mm；d为缺陷深度,mm;M为Folias系数;L为缺陷轴向长度,mm。

当L2/Dt≤50时：

(12)

当L2/Dt>50时：

(13)

综合式(11)～(13)可知，缺陷深度d和缺陷长度L是影响管道失效的重要因素，且对于在役运行埋地管道而言，该缺陷变量难以获取。结合非接触磁记忆检测优势与第2.2,2.3节内容，建立埋地管道可靠性评价模型。

为此，分别求解ΔH(y)关于d、k(x,y)关于L的偏导：

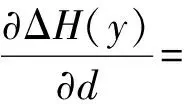
(14)

(15)

从式(14)(15)可知，偏导存在且大于零，即反函数存在：

d(ΔH(y),P)=(1.06-0.0408P)ln{[16.89-ΔH(y)]

÷[ΔH(y)-2.95exp(0.126P)

-40.89]}+4.00

(16)

L(k(x,y),P)=(7.88-0.1485P)ln{[k(x,y)

-30.93]/[0.30exp(0.1664P)

+2.21]}+2.46

(17)

用式(16)(17)分别替换式(11)～(13)中d和L，联立式(10)(11)，即可得到基于非接触磁特性参数的可靠性模型：

(18)

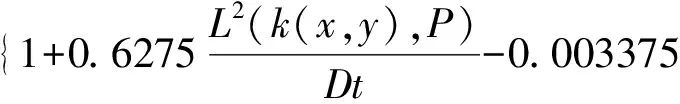
(19)

其中：L2(k(x,y),P)/Dt≤50

(20)

其中：L2(k(x,y),P)/Dt>50

3.3 基于MCMC的可靠度计算

建立可靠度模型后，在计算可靠度时，一般利用蒙特卡洛方法。但由于常规的蒙特卡洛方法在计算过程中，随机产生的样本之间存在独立性，不考虑当前状态对未来状态的影响，往往需要抽取大量样本，收敛速度较慢。

由于马尔科夫链能够考虑到样本之间的关联性与时变性，且收敛速度较快，故在传统蒙特卡洛法的基础上引入马尔科夫链，求解埋地管道的可靠度，利用当前管道运行状态对后续时刻的可靠度进行评价，解决动态性问题，克服工程实际中历史样本难以获取的问题。计算可靠度模型式(18)概率值，即可靠度R(t)：

R(t)=P(Z=r-s>0)

=Pr(r)Ps(s)

(21)

式(21)中Pr(r),Ps(s)分别为失效应力r及实际应力s的累积概率，其计算公式分别为：

(22)

(23)

基于Metropolis-Hasting (M-H)采样的可靠度模型参数后验分布计算流程(如图14所示)如下：(1)设定状态转移次数阈值m，需要的样本个数N；(2)从前述先验概率分布采样得到初始状态值x0，设定t=0；(3)从条件概率分布Q(x∣xt)中采样得到样本值x*，从均匀分布中采样u～[0,1]。如果u<α(xt,x*)，则接受转移(即xt+1=x*)，否则不接受转移；(4)重复步骤(3)直至达到状态转移次数阈值，生成的样本集即为待求参数Pr(r),Ps(s)的后验分布π(x)。

于是有N个r及N个s值，构成了r和s的随机抽样数组。若ri>si，则可靠；最后，确定ri>si的总次数Ni，则有：

R(t)=Ni/N

(24)

图14 Metropolis-Hasting采样流程图Fig.14 Metropolis-Hasting sampling flow chart

3.4 可靠度计算结果及分析

利用试验管道基本参数与试验数据，对不同压力下的R(t)进行计算，获得埋深1 m，不同ΔH(y)与k(x,y)的可靠度R(t)云图。

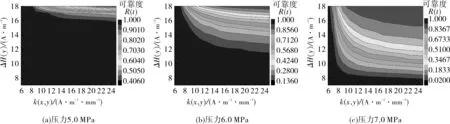
图15 在不同ΔH(y)与k(x,y)条件下的R(t)云图

由图15可看出，在一定压力下，埋地管道可靠度R(t)随着磁特性参数数值的增加而减小；磁特性参数一定时，R(t)随压力的增加而显著减小，结果符合工程实际中R(t)的变化规律。

3.5 算法比较

相同条件下，采用传统MC算法计算的可靠度与MCMC方法计算的结果进行对比校验。图16示出相同条件下两种方法计算的可靠度收敛曲线,MCMC方法在收敛速度上明显优于传统MC方法，后者在抽样进行到26 000次才显现收敛趋势；而前者在抽样进行到5 500次左右时即成功收敛，两种方法抽样次数相差近5倍。

同时，MCMC方法在收敛稳定性上也显著优于传统MC方法，分别对MC与MCMC方法进行10次重复计算，由图17对比看出，MCMC方法计算结果的离散程度明显小于传统MC方法，稳定性更好。对10次重复试验获得的可靠度R(t)进行量化计算，MCMC方法的方差仅为0.041 7，而MC方法的方差为0.102 6。

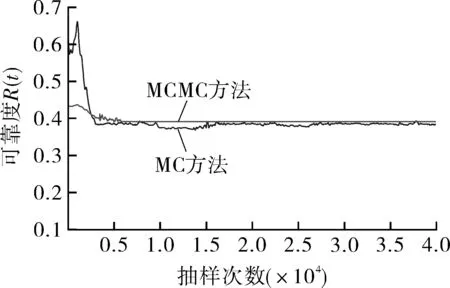
图16 MC与MCMC之间的可靠度R(t)收敛曲线对比Fig.16 Comparison of R(t) convergence curves betweenMC and MCMC

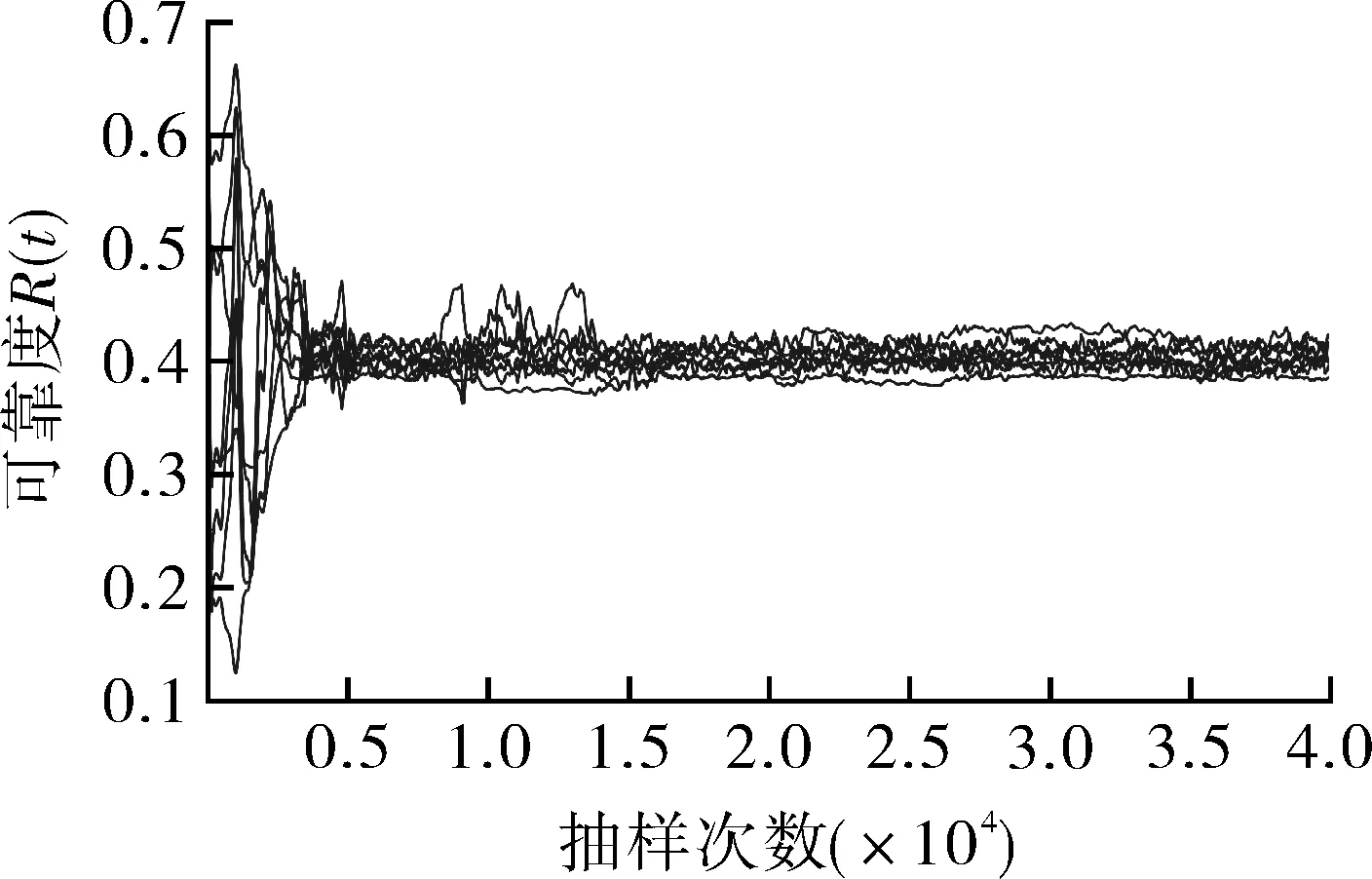
(a)MC方法

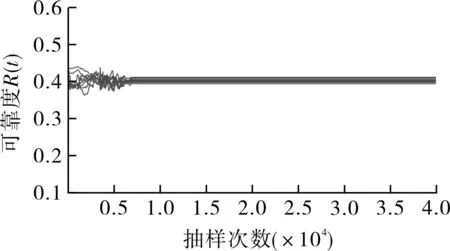
(b)MCMC方法图17 MC与MCMC收敛稳定性对比Fig.17 Convergence stability comparison betweenMC and MCMC

MCMC方法在收敛速度和稳定性上的优势，使埋地管道可靠度计算所需时间大大缩短、精度大大提高，提升了该方法的工程实用性与有效性。

4 可靠度模型验证

为了对所建可靠度模型进行现场验证，对大庆采油五厂杏南中转站某埋地输油管道进行现场试验。该埋地管道平均埋深为1 m，材质为L245N管线钢，其相关参数如表1所示。

表1 管道参数Tab.1 Parameters of the pipeline

通过现场试验测得的数据，在利用工程图纸排除管线中弯头、法兰等干扰因素对信号的影响后，利用第3.3节中构建的可靠度模型，对该埋地管道进行可靠度预测。其中可靠度异常区段如表2第2列所示，进一步对预测的可靠度异常区段进行开挖验证，同时进行超声波测厚复检，结果如表2第4列所示，其中区段610～620 m出现泄漏，开挖后现场照片见图18，利用管道实际缺陷参数，采用Modified B31G标准对异常区段进行可靠度验证计算，其结果见表2第3列所示。

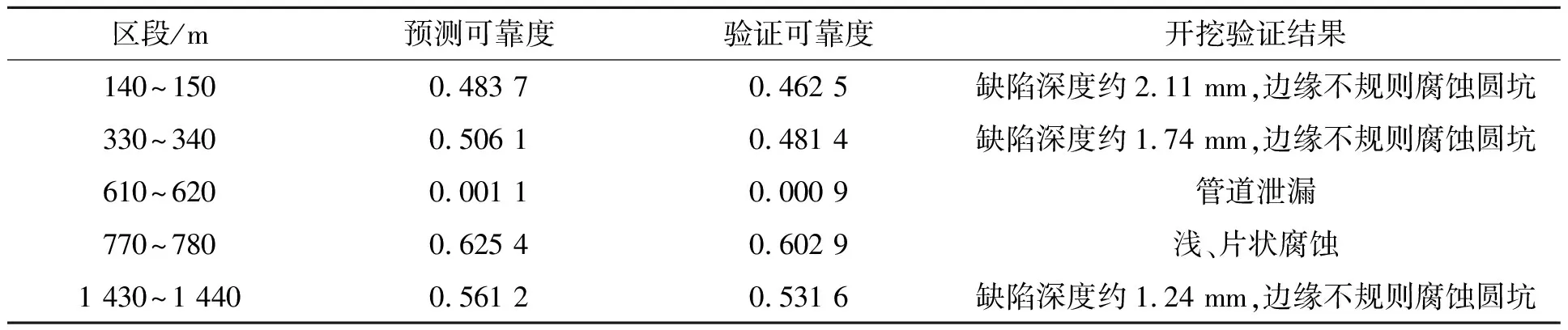
表2 埋地管道可靠度异常区段Tab.2 Reliability abnormal section of buried pipeline

由表2第2，3列可以看出，基于磁特性参数、利用所建的可靠度模型所得的可靠度，与基于实际缺陷尺寸、利用Modified B31G标准计算的验证可靠度之间的平均误差约为8.24%，因此本文所提出的埋地管道可靠度定量评价模型具有有效性，为在不开挖情况下，计算在役埋地管道可靠度，提供了一种新的方法。

图18 泄漏区段管道开挖结果Fig.18 Excavation verification photo of the pipelinein the leaking section

5 结论

(1)引入Kendall相关系数，对试验所获非接触磁特性参数的相关性进行定量研究，发现ΔH(y)和k(x,y)可分别敏感地反映并表征d,L变化规律。

(2)分别非线性拟合ΔH(y)与d、k(x,y)与L之间的回归函数，并优选修正系数，经检测样本验证得知，公式修正后最大误差分别为6.07%和8.79%。

(3)基于非接触磁特性参数，结合Modified B31G评价标准，在蒙特卡洛法基础上，引入马尔科夫链，建立埋地管道可靠度定量评价模型。与MC方法相比，MCMC方法计算可靠度所需抽样次数大幅减少，稳定性更好。

(4)现场试验结果表明，开挖后利用管道实际缺陷尺寸，利用Modified B31G评价标准直接计算的验证可靠度，与本文所建的可靠度定量评价模型计算的可靠度之间平均误差约为8.24%，这为实际工程埋地管道非接触检测与可靠度定量评价提供了一种新的思路。