一类非自治随机积分-微分方程的均方渐近概自守温和解

姚慧丽, 刘冬玥， 孙源源, 王晶囡

(哈尔滨理工大学 理学院， 哈尔滨 150080)

0 引 言

1962年，Bochner给出了概自守函数的有关概念[1]，1981年，N’Guérékata给出了渐近概自守函数的定义[2]，2008年，Liang等给出了伪概自守函数的有关概念[3]。自概自守型函数有关理论被提出以来，数学工作者们将其应用到各类方程中，讨论方程的概自守型解的存在性问题[4-8]。2010年，Fu 等提出了均方概自守随机过程的概念[9]，随后均方渐近概自守随机过程和均方伪概自守随机过程有关理论相继被给出。从应用的角度看，随机微分方程尤为重要，因为这种方程将随机性纳入了数学描述中。2013年，Li等简单介绍了方程(1)的研究背景，并研究了该方程的均方概自守温和解的存在性和唯一性[10]。其中：t∈R，{A(t)}:D(A(t))→L2(P,H)是一族稠定线性闭算子(有可能是无界的)，满足所谓的“Acquistapace-Terreni”条件，B和C分别是L1(0,∞)和L2(0,∞)中的卷积型内核，W(t)是定义在过滤概率空间的(Ω,F,P,Ft)上的一个双边一维标准的布朗运动。方程(1)如下：

(1)

近些年讨论各类随机微分方程的均方概自守解和均方伪概自守解的文献较多[11-18],相比之下，关于方程的均方渐近概自守解研究的文献较少，故本文主要研究方程(1)的均方渐近概自守温和解的存在性和唯一性。

1 预备知识

定义1一个随机过程x(t):R→L2(P,H)被称为是随机有界的，是指存在一个常数M>0满足

E‖x(t)‖2≤M

对所有t∈R成立。

定义2一个随机过程x:R→L2(P,H)被称为是随机连续的，是指对于任意s∈R,有

成立。

定义3设X∈C(R,L2(P,H))，如果对任意的实数序列{s′n}n∈N,都存在它的一个子列{sn}和一个随机过程Y:R→L2(P,H)满足：

则称X是均方概自守的，此类X的全体记为AA(R,L2(P,H))。

定义4设F∈C(R,L2(P,H))，如果F可分解为：

F=G+φ,G∈AA(R,L2(P,H)),φ∈SMC0(R,L2(P,H))

其中

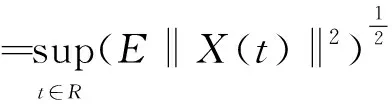
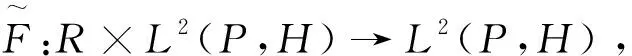
和

对任意的t∈R和X∈K成立，则称F是关于t∈R且一致对X∈K(K是L2(P,H)任意紧子集)均方概自守的，此类F的全体记为AA(R×L2(P,H),L2(P,H))。

定义6设F∈C(R×L2(P,H),L2(P,H))，如果F可分解为：

F=G+φ,G∈AA(R×L2(P,H),L2(P,H)),φ∈SMC0(R×L2(P,H),L2(P,H))

其中

SMC0(R×L2(P,H),L2(P,H))

则称F是关于t∈R且一致对X∈K(K是Lp(P,H)的任意紧子集)均方渐近概自守的，此类F的全体记为AAA(R×L2(P,H),L2(P,H))。

定义7X上的有界线性算子集合{U(t,s):t≥s,t,s∈R}，如果满足：

(1)U(s,s)=I，U(t,s)=U(t,r)U(r,s)(t≥r≥s,t,r,s∈R);

(2)(t,s)∈{(τ,σ)∈R2,τ≥σ}→U(t,s)是强连续的。

那么它被称为是卷积族。

‖(A(t)-λ0I)R(λ,A(t)-λ0I)×[R(λ0,A(t))-R(λ0,A(s))]‖≤L|t-s|α|λ|β

对t,s∈R,λ∈∑θ∶={λ∈C-{0}∶|argλ|≤θ}。

定义8设(X(t))t∈R是一个随机连续的随机过程，如果它满足下列的随机积分方程：

(2)

对于所有t≥a和每一个a∈R，则称(X(t))t∈R是方程(1)在R上的一个温和解。

2 主要结论

主要对方程(1)的均方渐近概自守温和解的存在性以及唯一性进行讨论，有以下结论：

定理1若方程(1)满足以下假设：

(H1)由满足“Acquistapace-Terreni”条件一族稠定线性闭算子A(t):D(A(t))⊂L2(P,H)→L2(P,H)生成的卷积族{U(t,s)}是一致指数稳定的，也就是存在常数M≥1和δ>0满足：

‖U(t,s)‖≤Me-δ(t-s)，∀t≥s

(H2)卷积族{U(t,s),t≥s}满足下列条件：对任意的实数序列{s′n}n∈N，都存在它的一个子列{sn}满足对任意的ε>0,存在一个N∈，满足当n>N时,有：

‖U(t+sn,s+sn)-U(t,s)‖≤εe-δ(t-s)

‖U(t-sn,s-sn)-U(t,s)‖≤εe-δ(t-s)

对所有的t≥s，其中δ>0是假设(H1)中所取常数。

(H3)函数Fi:R×L2(P;H)→L2(P;H),(t,X)Fi(t,X)(i=1,2)和G:R×L2(P;H)→L2(P;H),(t,X)G(t,X)关于t∈R且一致对于每一个X∈L2(P;H)是均方渐近概自守的。另外F1,F2和G是相对于X一致关于t满足Lipschitz条件的，即存在常数Ki>0(i=1,2,3)使得

E‖Fi(t,X)-Fi(t,Y)‖2≤KiE‖X-Y‖2,i=1,2

E‖G(t,X)-G(t,Y)‖2≤K3E‖X-Y‖2

对于所有的随机过程X,Y∈L2(P;H)，t∈R。

则方程(1)存在唯一的均方渐近概自守温和解X(t)，且可表示为：

(3)

式中t∈R。

证明在AAA(R,L2(P,H))上定义映射φ：

(4)

由引理1可得，AAA(R,L2(P,H))在‖·‖∞下是一个Banach空间。下证φ是一个从AAA(R,L2(P,H))到自身的压缩映射。

第一步： 先证φ是一个从AAA(R,L2(P,H))到自身的映射。

先在AAA(R,L2(P,H))上定义三个非线性算子，如下：

为证(φX)(t)∈AAA(R,L2(P,H)),仅需证(φiX)(t)∈AAA(R,L2(P,H)),i=1,2,3。结合假设(H3)和文献[21]中引理10，可知F1(s,X(s))∈AAA(R,L2(P,H)),所以可记F1(s,X(s))=f1(s)+f2(s)，其中

f1(s)∈AA(R,L2(P,H))，f2(s)∈SMC0(R,L2(P,H))

因此有

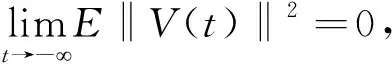
(5)

V(t)∈SMC0(R,L2(P,H))

综上得(φ1X)(t)∈AAA(R,L2(P,H))。

下证(φ2X)(t)∈AAA(R,L2(P,H))。结合假设(H3)和文献[21]中引理10可知F2(s,X(s))∈AAA(R,L2(P,H))，因此记F2(s,X(s))=I1(s)+I2(s),其中I1(s)∈AA(R,L2(P,H))，I2(s)∈SMC0(R,L2(P,H))。故有:

由假设(H1)、(H2)、(H3)及文献[21]可知，L(t)∈AA(R,L2(P,H))，根据AAA(R,L2(P,H))的定义，故只需证N(t)∈SMC0(R,L2(P,H))。

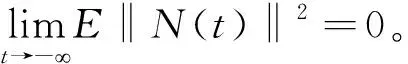
(6)

对式(6)最后三部分分别加以讨论。

对于第一部分，结合Cauchy-Schwarz不等式和(H1)可得：

对第二部分，结合Cauchy-Schwarz 不等式和(H1)可得：

整理可得：

(7)

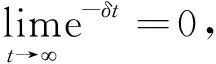
证明(φ3X)(t)∈AAA(R,L2(P,H))的过程与证明(φ2X)(t)∈AAA(R,L2(P,H))的过程类似，故省略。至此证得了式(4)定义的φ是从AAA(R,L2(P,H))到自身的映射。

第二步： 证明φ是一个压缩映射。根据不等式(a+b+c)3≤3a2+3b2+3c2,对任意X,Y∈AAA(R,L2(P,H))可得：

E‖(φX)(t)-(φY)(t)‖2

=E‖{(φ1X)(t)+(φ2X)(t)+(φ3X)(t)}-{(φ1Y)(t)+(φ2Y)(t)+(φ3Y)(t)}‖2

(8)

对式(8)的最后三项分别加以讨论。利用Cauchy-Schwarz不等式和上述列出(H1)～(H3)，可得：

(9)

对于第二部分，用第一部分相同的方法，可得：

(10)

对于第三部分，将再一次使用Ito等距积分、Cauchy-Schwarz不等式以及(H1)～(H3)可得：

由式(9)～式(11)可得：

(11)

也就是说：

(12)

结合式(12)有：

(13)

由‖·‖∞的定义并结合式(13)得：

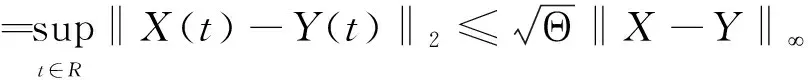
由(H4)可得映射φ为关于Θ的压缩映射，因此，由压缩定理可得，φ在AAA(R,L2(P,H))上有且仅有一个X，满足φX=X,即：

对任意的t∈R成立。上式即为前面的(3)式。将t=a代入(3)式,两端同时乘以U(t,a)，并结合U(t,σ)=U(t,a)×U(a,σ)，对于一切t≥s成立，可得：

(14)

又对t≥a有，将式(14)代入温和解的定义式(2)，有：

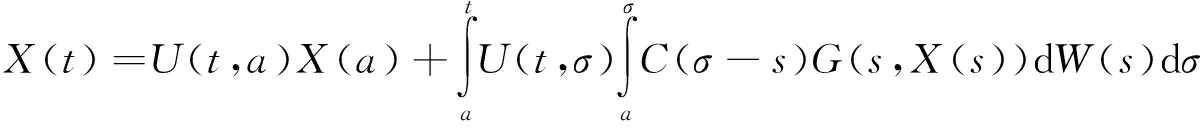
这就证明了式(2)与式(3)等价，因此，可得方程(1)有唯一的均方渐近概自守温和解。