分数阶Schrödinger-Hirota方程的显示解
何黎霞, 孙峪怀
(1.四川工商学院 计算机学院, 成都 611730; 2.四川师范大学 数学科学学院, 成都 610011)
0 引 言
分数阶非线性偏微分方程具有浓厚的物理背景和重要的科学价值。它不但可以描述反常扩散的问题,而且在黏弹性流体力学、机器人、数字图像处理、控制论、金融和热传导等众多领域中也有广泛应用。
为了更好地理解分数阶非线性偏微分方程所刻画的变化现象的内在规律以及现实背景,方程的显示精确解的构建尤为重要。近些年来,已有许多成功求解分数阶非线性偏微分方程的显示解的有效方法,如广义G′/G-展开法[1]、F-展开法[2]、改进的Kudryashov方法[3]、不变子空间方法[4-6]、动力系统分支方法[7-8]、exp-函数法[9]、改进的子方程法[10-11]、扩展sinh-Gordon方程展开法[12]、G′/(G′+G+A)展开法[13]、李群分析法[14]、(G′/G,1/G)-函数展开法[15]和完全判别系统法[16-17]等。
本文考虑分数阶Schrödinger-Hirota方程[18]:
(1)

分数阶Schrödinger-Hirota方程是描述光孤子在色散光纤中的传播的重要模型,因此构建它的精确行波解具有重要的现实意义。Hadi等用展开直接代数方法构造了方程(1)的三角函数解、有理函数解以及双曲函数解[19]。本文拟用完全判别系统法研究方程(1),以构造该方程更为丰富的显示精确解。
1 方法的简述
刘成仕借助多项式的完全判别系统,首次提出了完全判别系统法求解非线性偏微分方程[20-22]。该方法的基本思想很简单,并且也适用于求解分数阶非线性偏微分方程。
考虑如下整合分数阶偏微分方程:
P(u,Dtαu,Dxβu,…)=0
(2)
式中P是关于待求函数u=u(x,t)及其偏导数的多项式。首先借助分数阶复变换和整合分数阶导数,将方程(2)转化为如下常微分方程:
u′(ξ)=G(u,δ1,δ2,…,δm)
式中δ1,δ2,…,δm为参数。再将上式改写成积分形式:
式中ξ0为积分常数,G(u,δ1,δ2,…,δm)是关于u的多项式。通过确定参数δ1,δ2,…,δm的取值范围,可以得到积分式的不同的解,进而得到方程(2)的精确行波解。
2 分数阶Schrödinger-Hirota方程显示解的构造
假设方程(1)有如下形式的解:
(3)
式中系数ω和η是常数。引入式(3),可得
(4)
(5)
(6)

(7)


φζ2=4φ(φ2+p1φ+p2)
(8)


情形1 当Δ=0时,由于φ>0,有
(9)
若p1<0,由式(9)可以得到方程(1)有如下形式的解:
若p1>0,由式(9)可以得到方程(1)有如下形式的解:
若p1=0,由式(9)可以得到方程(1)有如下形式的解:
情形2 当Δ>0,p2=0时,由于φ>-p1,有
(10)
若p1<0,由式(10)可以得到方程(1)有如下形式的解:

若p1>0,由式(10)可以得到方程(1)有如下形式的解:
情形3 当Δ>0且p2≠0时,令γ1<γ2<γ3,且其中有一个为零,其余两个为F(φ)=0的两个实根,作等量变换φ=γ1+(γ2-γ1)sin2φ,有
(11)
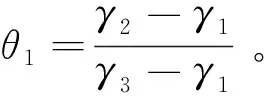
值得注意的是当θ1=0时,Jacobi椭圆函数sn将会退化成为函数sin;当θ1=1时,Jacobi椭圆函数sn将会退化成为函数tanh。因此,可以得到方程(1)有如下形式的解:

(12)

由式(12)可以得到方程(1)有如下形式的解:
值得注意的是,当θ2=0时,Jacobi椭圆函数cn将会退化成为函数cos;当θ2=1时,Jacobi椭圆函数cn将会退化成为函数sech。因此,可以得到式(1)有如下形式的解:
文中得到的显示解中u1(x,t)、u2(x,t)、u6(x,t)、u7(x,t)以及u10(x,t)为扭结波解,u3(x,t)、u5(x,t)以及u9(x,t)为三角函数解,u4(x,t)为有理函数解,u8(x,t)、u11(x,t)以及u12(x,t)为Jacobi椭圆函数解,u13(x,t)为周期波解,u14(x,t)为暗孤立波解。
3 结 论
本文将完全判别系统法应用于求解分数阶Schrödinger-Hirota方程,得到了六类显示精确解,包括扭结波解、三角函数解、有理函数解、Jacobi椭圆函数解、周期波解和暗孤立波解。与文献[19]的结果作对比,u1(x,t)、u2(x,t)以及u3(x,t)与其结果一致,其余解均为新显示解。这些新显示精确解有助于更好理解光孤子在色散光纤中的传播的物理本质。同时,结果表明完全判别系统法是求解非线性分数阶Schrödinger-Hirota方程的有效方法,具有简单便捷的优点。

