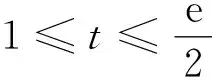具有测度积分边界条件的非线性Hadamard分数阶微分方程的正解
杨尊凯, 顾海波, 李 宁, 孙会贤, 田春平
(新疆师范大学 数学科学学院, 乌鲁木齐 830017)
0 引 言
本文主要研究以下具有测度积分边界条件的非线性Hadamard分数阶微分方程:
Dαu(t)+f1(t,u(t),v(t))=0, 1 Dαv(t)+f2(t,u(t),v(t))=0, 1 u(1)=u′(1)=0 (1) v(1)=v′(1)=0 式中:Dα和Iα分别是α阶Hadamard分数阶导数和积分,2<α≤3,1<σ≤e;A(t)是单调递增非负的可测函数。假设以下条件成立: H1:fi(i=1,2)在[1,e]×R+×R+上是非负连续函数; H2:在[1,e]上, 近年来,分数阶微分方程边值问题得到了许多学者的关注和深度研究,并且得出了大量的关于分数阶微分方程边值问题的结果。本文研究的 (1) 式正解,尚未有学者进行研究,尤其是具有测度积分边界的分数阶微分方程研究甚少,但也有学者通过使用单调迭代方法研究了分数阶微分方程边值问题解的存在性和唯一性[1-5],文献[1]通过混合单调算子的不动点定理,研究了含积分边界条件的奇异分数阶微分方程正解的唯一性: [0,+∞)是连续函数,a,h∈C(0,1),A是有界变差函数。 许多学者通过运用不动点定理研究了Caputo 类型的分数阶微分方程[6-9],如文献[6],利用增凹算子的不动点定理,研究了一个新的分数阶微分方程组正解的存在性和唯一性: 式中:cDθ10+、cDθ20+是Caputo分数阶导数;θi∈(2,3);fi: [0,1]×(-∞,+∞)×(-∞,+∞)→(-∞,+∞)是连续函数;Ai是正可测有界变差函数,ai: [0,1]→[0,+∞)是连续函数,此处i=1,2。近年来,Hadamard类型分数阶微分方程也备受学者关注,一些学者通过不动点定理等方法研究了Hadamard类型分数阶微分方程[10-15],文献[10]通过不动点定理研究了具有积分边界条件的非线性Hadamard分数阶微分方程组的正解: 式中:Dβ是β阶Hadamard分数阶导数,2<β≤3;fi(i=1,2)在[1,e]×R+×R+上是非负连续函数。 定义2.1[15]函数u: [1,∞)→R的α阶Hadamard分数阶导数定义为: 式中:n=[α]+1;[α]表示实数α的整数部分;log(·)=loge(·)。 定义2.2[15]函数u: [1,∞)→R的α阶Hadamard分数阶积分定义为: 等式右部分表示积分存在。 引理2.3令x,y∈C[1,e],C[1,e]是指[1,e]上连续函数所构成的空间,积分边值问题∶ (2) 可以转换成以下Hammerstein型积分方程: (3) 式中: (4) δ为大于零的常数: 证明对(2)式进行α阶积分,有: c1i,c2i∈R,i=1,2,3,再根据u(1)=v(1)=u′(1)=v′(1)=0,所以c12,c13,c22,c23=0,因此可以得到 根据条件: 可以推导出: 即: 令: 那么,c11,c21表示如下: - 类似地,也可以得到: 证明完毕。 通过引理2.3,方程(1)等同于以下Hammerstein型积分方程: (5) 引理2.4对任意的t,s∈[1,e],由式(4)定义的函数G1(t,s)满足下列不等式: 证明根据文献[8]的理论结果,令α∈(n-1,n],n∈N,3≤n,构造函数G(z,l): 函数G(z,l)假设如下: (R1)G(z,l)=G(1-l,1-z),对任意的z,l∈[0,1] (R2) Γ(α)k(z)q(l)≤G(z,l)≤(α-1)q(l),对任意的z,l∈[0,1] 因此,对任意的t,s∈[1,e],有∶ Γ(α)k(logt)q(logs)≤G(logt,logs)≤(α-1)q(logs) Γ(α)k(logt)q(logs)≤G(logt,logs)≤(α-1)k(logt) 令z=logt,l=logs,则函数G(z,l)=G1(t,s),所以I1和I2成立,证明完毕。 (6) 令E∶=C[1,e],‖u‖∶=maxt∈[1,e]|u(t)|,P∶={u∈E:u(t)≥0,∀t∈[1,e]},由此可知,(E,‖·‖)是实Banach空间,P是E上的锥。通过引理2.3以及引理2.4,定义算子Ti:P×P→P: (7) 对任意的t∈[1,e],有: T(u,v)(t)=(T1(u,v),T2(u,v))(t) (8) Ti:P×P→P,T:P×P→P×P是全连续算子,当且仅当(u,v)是算子T的不动点,因此可以通过(u,v)求解方程(1)。 证明仅证明T1(P×P)∈P0,通过引理2.4(I1)以及Γ(·)函数在[2,+∞)单调递增,对任意的t∈[1,e],有: 以及 因为α-1>1,所以对任意的u,v∈P,t∈[1,e],有: 证明完毕。 ω-Tω≠λω0, ∀λ≥0,ω∈∂Ω∩P,那么i(T,Ω∩P,P)=1 引理2.8[16]令E为实Banach空间,P为E上的锥。假设Ω⊂E是一个有界开集,并且0∈Ω,而 ω-λTω≠0,则i(T,Ω∩P,P)=1 为了后文表述方便,给出如下表示和相关假设条件: H3:存在常数a1i,b1i(i=1,2)≥0以及l1,l2>0满足下式: H4:存在常数a1i,b1i(i=1,2)≥0以及r1>0满足下式: 定理 3.1假设条件H1~H4成立,则方程(1)有一个正解。 证明令S1={(u,v)∈P×P:(u,v)=T(u,v)+λ(φ1,φ1),∀λ≥0},φ1是P0中一个固定元素,称S1是P×P中的有界集合,如果存在(u,v)∈S1使得: u(t)=T1(u,v)(t)+λφ1(t),v(t)=T2(u,v)(t)+λφ1(t),t∈[1,e] (9) 那么通过引理2.6,可以知道u,v∈P0。 (10) 通过式(9)对任意的t∈[1,e],有∶ u(t)≥T1(u,v)(t),v(t)≥T2(u,v)(t) (11) 根据算子Ti(i=1,2)的定义以及引理2.4和引理2.5可以得到: (12) (13) 结合条件H3,有: (14) 以及 通过进一步计算可得: 因此,存在常数M1>0,M2>0使得: (15) 这也就证明了S1在P×P中是有界的。如果选择 则对任意的(u,v)∈∂BR1∩P×P,∀λ≥0,有: (u,v)≠T(u,v)+λ(φ1,φ1) (16) 成立。因此,通过引理2.7,有: i(T,∂BR1∩(P×P),P×P)=0 (17) 接下来证明 (u,v)∈∂Br1∩P×P,∀λ∈[0,1],(u,v)≠λT(u,v) (18) 假设式(18)不成立,存在(u,v)∈∂Br1∩(P×P),λ∈[0,1],使得(u,v)=λT(u,v),这也就意味着对任意的t∈[1,e],有: u(t)≤T1(u,v)(t),v(t)≤T2(u,v)(t) (19) 通过引理2.4以及2.5可得: 将H4代入上述不等式,可得: 因此,可得: 所以,通过H4可以知道∶ i(T,∂Br1∩(P×P),P×P)=1 (20) 由式(14)以及式(18)可得: =0-1=-1 令a11=20,a12=700,b11=400,b12=10,a21=3,a22=5,b21=2,b22=3,那么: a11(k1+k3δ)+a12k4≈0.232+0.595<1,b12(k1+k4δ)+b11k3≈0.039+0.252<1 a21(k2+k5δ)+a22k6≈0.429 7+0.535<1,b22(k2+k6δ)+b21k5≈0.056 4+0.016 2<1 ≈1.758 5 a11(k1+k3δ)+a12k4≈0.232+0.623<1,b12(k1+k4δ)+b11k3≈0.116+0.268<1 a21(k2+k5δ)+a22k6≈0.389 7+0.064<1,b22(k2+k6δ)+b21k5≈0.390 6+0.019<1 因此,对任意的t∈[1,e],x,y∈R+,α1,α2>1。令f1(t,x,y)=(20x+400y)α1,f2(t,x,y)=(400x+10y)α2,由此可以得到: 因此条件H3和H4成立。
1 预备知识


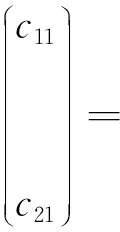













2 主要结果




3 例 子