大柳煤矿深部软岩巷道支护技术数值模拟研究

李治祥，王福奇，田斌，吴军，经来旺，张瀚文

(1. 华亭煤业大柳煤矿有限公司，甘肃省平凉市，744100；2.安徽理工大学光电和力物学院，安徽省淮南市，232001；3. 安徽理工大学深部煤矿采动响应与灾害防控国家重点实验室，安徽省淮南市，232001)

现阶段我国西部地区煤炭开采过程中井下巷道变形破坏程度十分严重，面临着严峻的软岩巷道支护难题[1]。以甘肃华亭煤业大柳煤矿为例，1405工作面进风巷道掘进初期便发生严重底鼓变形，随后全断面收缩变形，局部区域受淋水影响支护结构近乎失效。具体表现在顶板最大下沉量达800 mm，帮部最大内移量达1 000 mm，墙角最大鼓出量达1 200 mm，底鼓最大变形量达1 800 mm。目前该通风巷道已开展多轮刷帮卧底再支护工作(由于井工矿井巷道受地压的原因，巷道两侧会往回聚，巷道的顶板和底板会产生下沉和底鼓，这样巷道的断面就不够，会带来不安全因素，这时就需要对巷道两侧和底板进行修复，修复巷道两帮就叫“刷帮”，修复底板就叫“卧底”，也叫“起底”)，但变形情况仍然没有得到改善。

学者们针对软岩巷道大变形问题给出了多种支护方案[2-5]，例如薛维培在许疃煤矿南翼运输大巷支护设计时提出锚杆与金属支架相互增强技术[6]；彭巍针对大雁矿区软岩巷道变形特征以及矿压作用情况，提出以锚喷支护为主体U型钢为辅的综合支护技术[7]；郭相平根据新元煤矿9102原回风巷大变形情况，设计出全锚索支护方案[8]。需要强调的是根据巷道所处地质条件、围岩应力状态等制约因素不同，相应地支护设计方案也不相同。

笔者以甘肃华亭煤业大柳煤矿1406工作面回风巷道为研究对象，从蠕变变形控制问题入手，采用ABAQUS数值模拟方法研究锚杆+锚索+注浆一体化支护对巷道围岩变形的控制情况，为支护方案优化设计提供参考依据。

1 工程概况

1406工作面回风巷道与1405工作面采空区相邻，巷道断面为梯形，上顶宽4.70 m、下底宽5.40 m、高4.55 m，巷道两帮和底板均处于4号煤层，煤层埋深在500～600 m，可采厚度4.46～8.29 m，普氏系数0.7，含夹矸0～2层，夹矸厚度0～0.6 m，4号煤层围岩柱状如图1所示。由于1406工作面回风巷道面临2个附近工作面重复采动作用，巷道围岩受到二次扰动影响，应力分布更加复杂且支护难度较大。

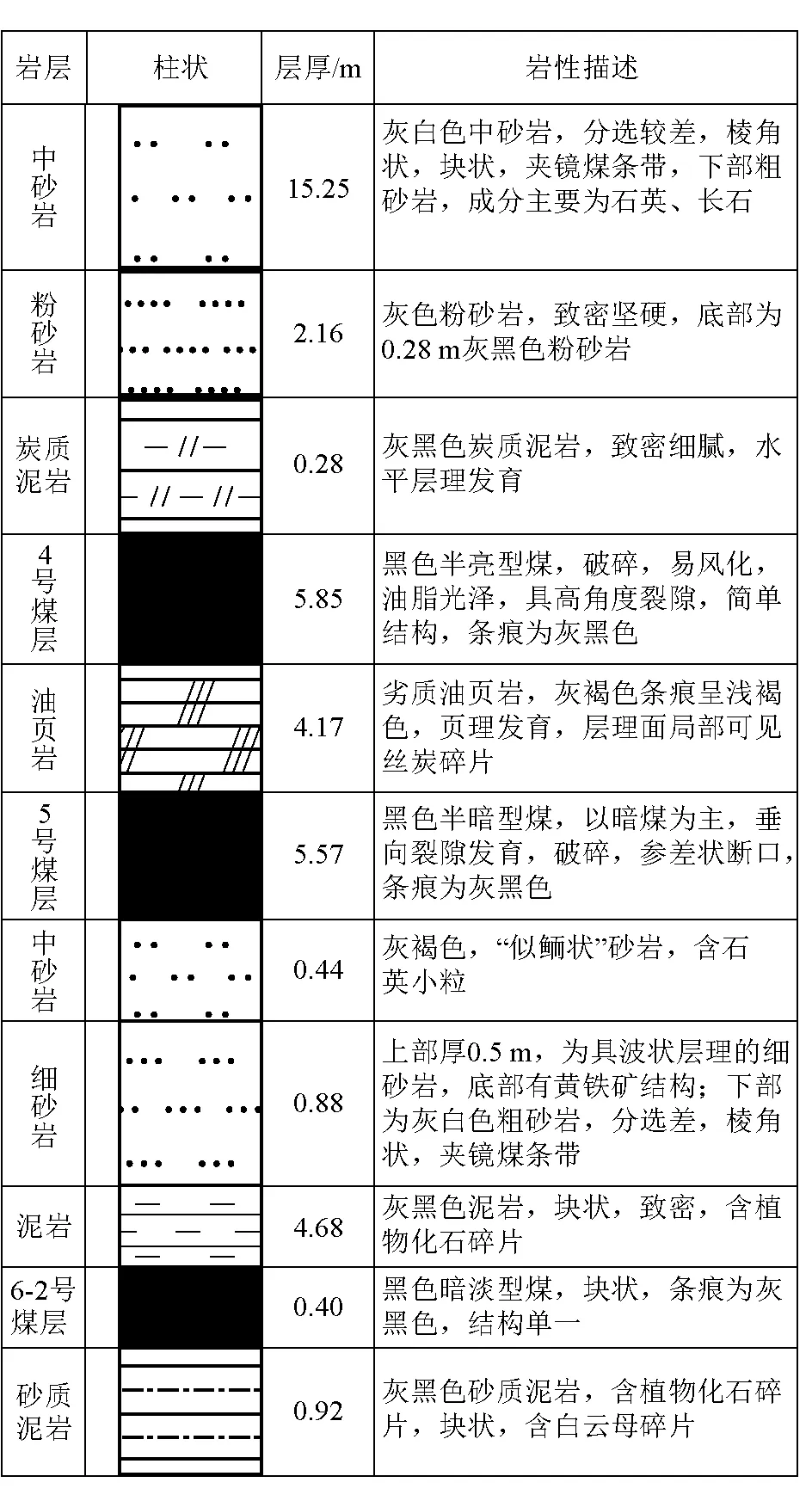
图1 4号煤层围岩柱状

2 数值模拟研究

2.1 蠕变本构模型

数值计算采用Drucker-Prager Creep模型：εc(t)′=Aqntm，两边同时对t求积分，如式(1)所示：

(1)

式中：εc(t)——某一时刻的应变；

A、m、n——蠕变参数；

q——围岩压力；

t——时间；

c——常数，取0。

2.2 模型介绍

数值分析模型为50 m×50 m×4 m的三维立体模型，岩层分布如图1所示，中间部分是煤层。巷道为一条等腰梯形巷道，上顶宽4.70 m，下底宽5.40 m，腰长4.56 m，高4.55 m。围岩共划分出17 220个C3D8R结构单元，锚杆/锚索使用三维线作出，Assombly模块与岩体模型组装在一起，通过嵌入的方式定义锚杆/锚索与岩体之间地相互作用，共划分出1 659个T3D2桁架单元。模型左右边界X方向位移、前后边界Y方向位移均设定为零，上覆岩层压力12.575 MPa，重力加速度10 m/s2，水平侧压系数0.75[9]，模型荷载及边界条件如图2所示。

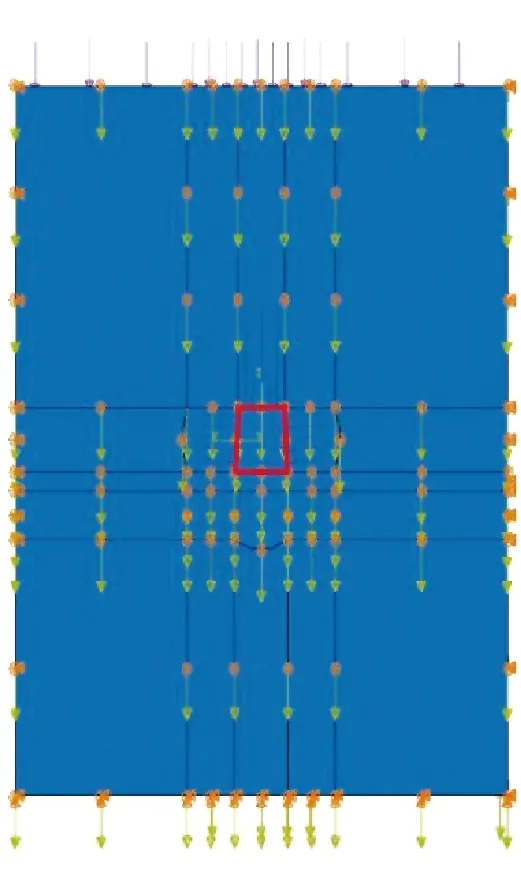
图2 模型荷载及边界条件

2.3 支护方案设计

采用锚杆+锚索+注浆一体化支护方案，顶板锚杆采用Φ22 mm×2 400 mm左旋无纵筋螺纹钢锚杆，两帮采用Φ17.8 mm×3 650.0 mm高强钢绞线锚索，间排距均为800 mm×800 mm，顶板锚索采用Φ21.8 mm × 7 300.0 mm高强钢绞线锚索，布置形式为3-4-3交错排列，间排距为1 500(1 600) mm×800 mm。顶部长锚索与短锚杆交错布置，具体锚杆/锚索断面布置如图3所示。由于受地下水和局部淋水影响，巷道底板岩层泥化现象非常严重，故在锚杆+锚索支护基础上，分别进行底部注浆和三帮注浆，注浆范围为巷道底部和帮部顺其方向向外延伸5.5 m的圆弧区域[10]。数值计算过程中，将模型分为上部围岩、煤体、注浆后煤体、下部围岩，相应的计算参数见表1。

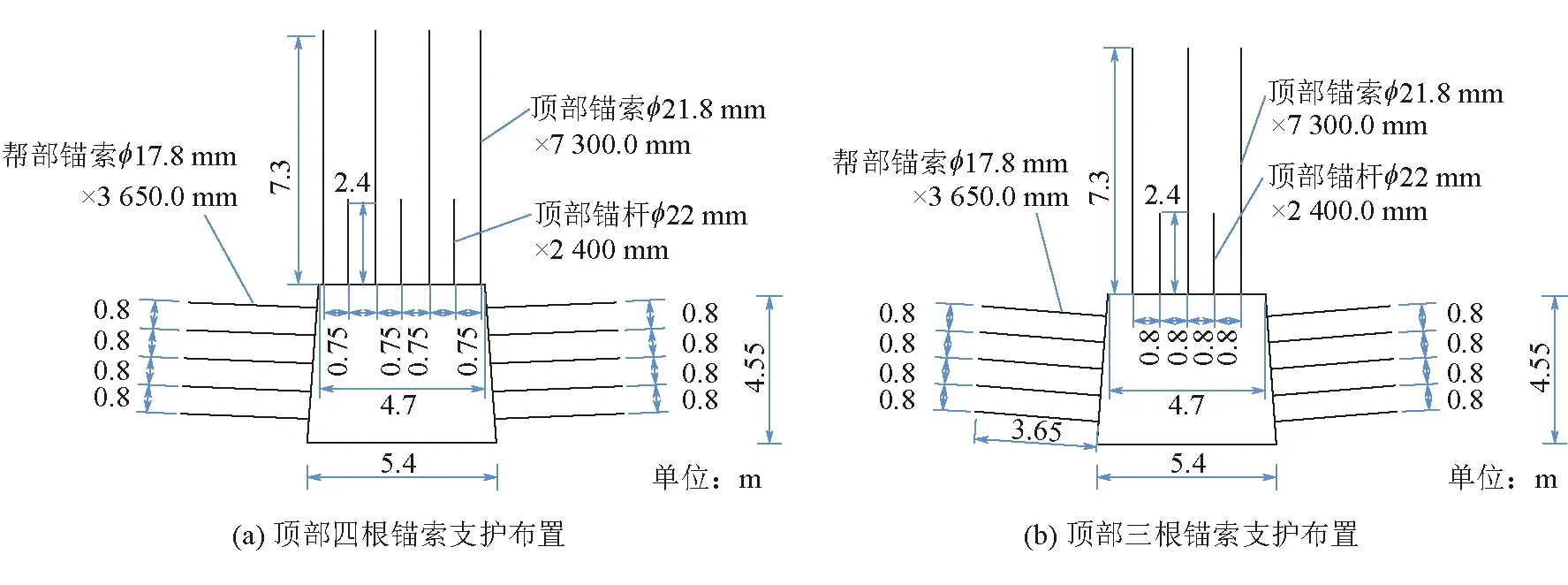
图3 锚杆/锚索3-4-3断面布置

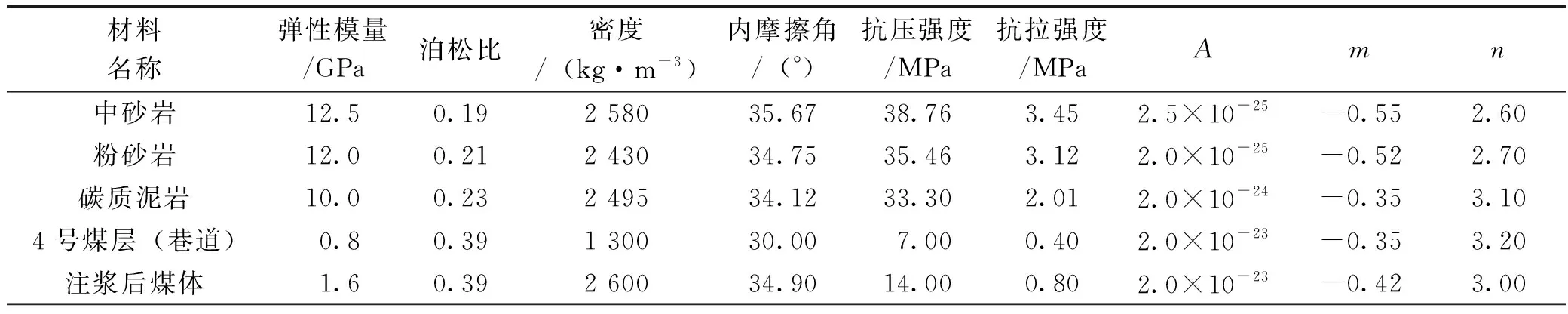
表1 数值计算参数

续表1

3 数值计算结果分析

为了更清晰地分辨不同方案支护效果的差异，共开展了4种支护方案下的数值分析，依次是未支护、锚杆锚索支护、锚杆锚索支护+底部注浆、锚杆锚索支护+三帮注浆。

3.1 Mises应力分析

Mises是一种综合考虑了第1、第2、第3主应力的强度准则(主应力是指物体内某一点以法向量的微面积元上剪应力为零时的法向应力，根据受力物体内任意一点的应力状态，都可取1个直角坐标系(x、y、z)，使3个坐标轴分别与互相垂直的3个主应力方向重合，这3个轴就叫作主应力轴，又按主应力的大小，即σ1>σ2>σ3的顺序，分别称之为最大主应力轴、中间主应力轴和最小主应力轴)，可以用来评价疲劳、破坏等现象。Mises应力是基于剪切应变能的一种等效应力，其值见式(2)：

(2)

式中：σ——Mises应力；

σ1、σ2、σ3——第1、第2及第3主应力。

模拟不同支护方案下，3个月蠕变后Mises应力分布如图4所示。图4(a)中由于煤层较软的缘故，Mises最大应力位于巷道左右上方围岩内，最大值达到13.67×106Pa；图4(b)中Mises最大应力集中位置分布在巷道帮部和底部，近似呈闭合状，显然增加锚杆锚索支护后巷道帮部及底部Mises应力值增加；当对巷道底部进行注浆补强支护后，如图4(c)所示，最大应力主要集中在底部注浆区域；图4(d)则是三帮注浆补强支护后，Mises应力值得到明显提高，最大值达到15.01×106Pa，应力集中区域在巷道两帮位置且呈对称分布。

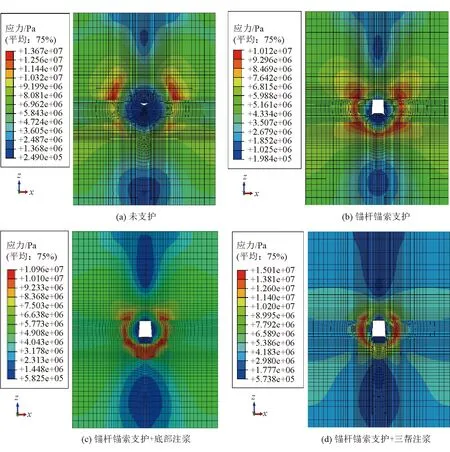
图4 不同支护方案3个月蠕变后应力分布

3.2 位移分析

不同支护方案下3个月蠕变后位移分布如图5所示。由图5(a)可以看出，巷道最大位移发生在巷道两帮处，左右两帮位移达到3.100 m，底鼓位移也发生较大的位移变形，达到1.376 m，巷道基本被堵死，不能进行正常的生产活动。由图5(b)可以看出，位移情况发生很大变化，两帮的位移变形由未支护的3.10 m减少为0.49 m，减少了84%以上，效果比较明显；底鼓位移变形由未支护的1.37 m减少为0.88 m，减少了0.49 m，两帮锚索对底鼓位移也产生了一定的抑制作用；顶板下沉由未支护的0.88 m减小为0.10 m，减少了0.78 m；顶部3-4-3式锚杆锚索支护对顶板下沉而言效果显著。相对于图5(b)而言，图5(c)中两帮位移由0.490 m减少为0.418 m，顶部下沉位移基本没有变化，底鼓位移由0.88 m减小为0.29 m，减少0.59 m，底鼓基本上得到了控制；底部注浆在锚杆锚索基础上对底鼓位移起到了很大的控制作用。相对于图5(c)而言，图5(d)中两帮位移变形由原来的0.418 m减小为0.245 m，减少0.173 m，但是底鼓位移由于两帮位移下沉，导致底鼓位移由原来的0.29 m增加为0.36 m，增加0.07 m。

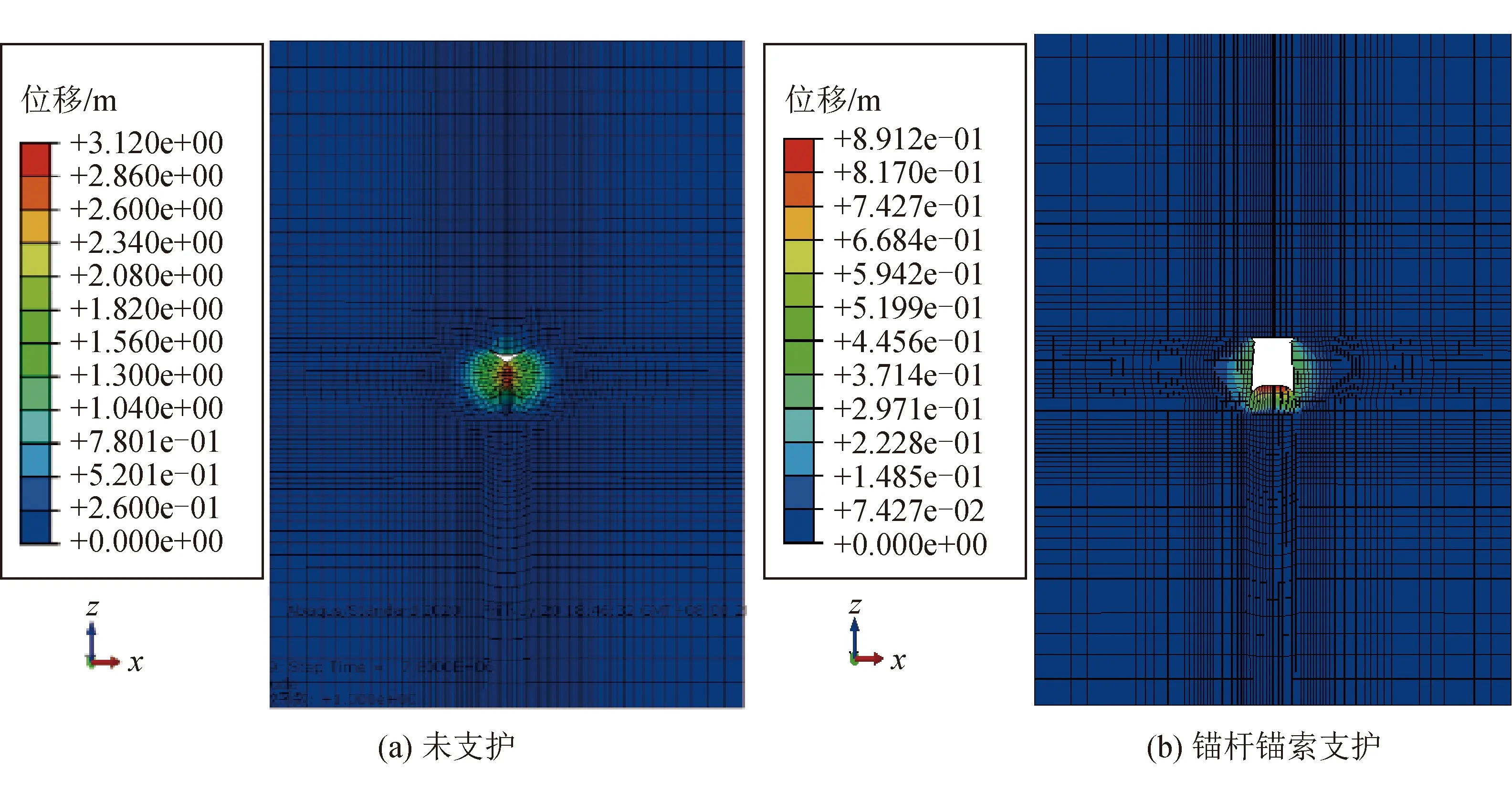
图5 不同支护方案3个月蠕变后位移分布云

3.3 三帮中点蠕变位移分析

为便于进一步分析，在巷道周边取4个关键点，关键点1是巷道顶板中点、关键点2和3是巷道左右两帮中点，关键点4是巷道底板中点，由此可绘制出三帮中点蠕变位移曲线[11]，如图6所示。由图6(a)可以看出，未加支护时，顶板下沉随着蠕变时间的增加而增大，3个月后下沉达到0.88 m，加锚杆锚索后顶板下沉起到抑制作用，最大达到0.08 m，相对于未支护减少了0.80 m，不同组合的注浆支护相对于加锚杆锚索支护而言，对顶板下沉位移基本没有起作用。由图6(b)可以看出，未加支护时，右帮位移随蠕变时间的增加而迅速增大，最大位移达到3.1 m，若不做支护处理，巷道会因两帮变形的增大而堵塞。加锚杆锚索支护后，两帮位移起到很好的抑制作用，随蠕变时间的增长位移达到稳定值。不同形式的注浆，尤其是三帮注浆后，两帮位移为0.24 m，达到巷道支护要求。由图6(c)可以看出，未加支护时，底鼓位移迅速增加，在3个月的蠕变时间内，最大底鼓量达到1.37 m，在锚杆锚索支护+三帮注浆时，底鼓变形最大达到0.36 m，但在锚杆锚索支护+底部注浆时，底鼓变形量最大为0.29 m，明显减少。

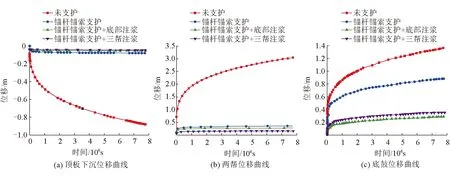
图6 三帮中点蠕变位移曲线

4 结论

(1)Mises应力分析结果表明，与未支护和帮顶锚杆锚索支护相比，注浆后的Mises应力有所提高，表明围岩的强度提高，注浆区能承担一部分应力集中情况，应力在巷道围岩相对较近的地方达到峰值，说明围岩松动圈半径变小。

(2)位移变形结果表明，与未支护巷道变形相比，在帮顶加锚杆锚索支护对巷道变形起到了很好的抑制作用，但是注浆支护后效果更加明显，可以达到安全生产的要求，进一步证明注浆支护在抑制巷道变形方面起到了良好的作用。

(3)巷道两帮和顶底板之间是相互作用的统一体，加强帮部支护在提高帮部强度的同时还能够改善顶底板受力状况，提高巷道整体稳定性。数值分析结果表明，控制帮部位移在一定程度上可以减少底鼓的上升量，说明帮部强化对底鼓位移有很好的抑制作用。