光电-静电复合驱动MEMS悬臂梁挠度分析
唐玉娟,陈昱松,王新杰,乔 锟
(1.金陵科技学院 智能科学与控制工程学院,江苏 南京 211169;2.南京理工大学 机械工程学院,江苏 南京 210094;3.中兴通讯西安研发中心,陕西 西安 710000)
微机电系统(Micro-electro-mechanical system,MEMS)具有体积小、重量轻、功耗低、精度高等优点,被广泛应用在测量、驱动和能量转换等多种功能技术中,其中精密驱动是MEMS技术的一个重要发展方向[1]。近年来,基于智能材料的微驱动方式被越来越多的研究者所青睐,如压电驱动[2]、形状记忆合金驱动[3]、磁致伸缩驱动[4]、电致形变驱动[5]和人工肌肉材料驱动[6]等方式。这些驱动方式需要电、热、磁场的刺激,虽具有各自的优势,但一般都需要传统的电磁激发源装置,易引起电磁噪声干扰,在洁净或真空操作环境中有较大的局限性。PLZT陶瓷在紫外光照射下可以基于光-电-热-力多能场耦合效应,将光能转化为电能,形成光致静电场,通过静电力最终实现光能到机械能的转化,这种基于PLZT陶瓷的光电-静电复合驱动方式,具有电磁兼容性好、驱动源清洁、可远距离控制等优点,为MEMS系统提供了一种理想的驱动方式。
近年来,众多学者针对PLZT陶瓷的反常光电效应和光致形变效应在主动控制和微驱动应用方面、PLZT陶瓷多能场耦合数学模型构建及完善方面展开了大量研究。在板壳的主动振动控制方面,Sun等[7]对PLZT陶瓷层合的柔性梁结构进行了主动控制研究;Chen等[8]通过进行尺寸效应的分析,建立了包括0-1和0-3极化的PLZT陶瓷单晶片和双晶片的微悬臂梁的本构方程,研究了与尺寸有关的尖端挠度、等效弯矩和阻塞力;在微驱动方面,黄家瀚等[9]提出了一种基于PLZT陶瓷双晶片的光驱动微夹钳;Lu等[10]利用PLZT陶瓷的光致伸缩效应提出了一种光驱动伺服系统,并进行了闭环伺服控制研究。在PLZT陶瓷多能场耦合数学模型构建及完善方面,黄家瀚等[11]将紫外光源照射下产生的温度变化影响因素引入到PLZT陶瓷的多物理场耦合的作用机理分析中,构建了更为完善的多能场耦合数学模型。针对PLZT陶瓷光致形变直接驱动存在响应速度较慢的问题,有学者尝试将PLZT陶瓷产生的光生电压施加到压电材料上,开展光电-压电复合控制的探索研究;如姜晶等[12]利用PLZT陶瓷产生光生电压驱动压电作动器,研究分析了光照强度、作动器电极表面积及作动器厚度等参数对光电-压电混合驱动性能的影响;乔锟[13]将PLZT陶瓷产生电压施加到PVDF层合柔性悬臂梁结构上,进行了光电-压电复合驱动柔性梁结构的驱动特性研究。基于PLZT陶瓷产生的高值光致电压开展光电复合驱动方式研究,为微驱动领域提供了一种全新的选择。
综上可知,学者们对PLZT陶瓷在振动控制、微驱动及本构模型构建方面做了大量工作;由于PLZT陶瓷所产生的光生电压与光致形变位移之间(即电能-机械能转换过程中)存在迟滞现象,即光生电压的响应速度(光能-电能转化速度)要远大于光致形变响应的速度。其主要原因是PLZT陶瓷在光照阶段产生了光致热场;如果利用PLZT陶瓷的光致形变特性对负载进行直接驱动,难以实现快速响应;PLZT陶瓷在光照期间可快速产生kV级光生电压,并迅速建立静电场;如利用静电力对负载进行驱动,其响应速度将大幅提高。但基于PLZT陶瓷所开展的光电-静电复合驱动研究仍属于初始研究阶段,尤其是对光电-静电场位置和光电-静电场强度变化引起执行机构挠度变化的研究更为欠缺。本文利用PLZT陶瓷的反常光电效应,提出一种光电-静电复合驱动MEMS柔性悬臂梁的新型驱动方式,建立光电-静电驱动悬臂梁的静态数学模型,并推导出其挠度解析式,归纳了悬臂梁自由端挠度随光电-静电场分布位置和光电-静电场强度的变化规律。这一研究成果为光电-静电复合驱动奠定理论基础,为实现大位移光电-静电复合驱动提供参考依据,具有一定的工程意义。
1 光电-静电复合驱动悬臂梁机构数学模型构建
本文基于光电-静电复合驱动机理,提出了一种基于PLZT陶瓷的光电-静电复合驱动悬臂梁的结构,如图1所示。在悬臂梁自由端一层表面上粘贴铜箔,形成可动铜箔极板;在与可动极板对应的绝缘基座支架上粘贴另一片铜箔,形成固定铜箔极板;可动极板与固定极板保持一定的距离。PLZT陶瓷电极两端分别通过导线与固定极板与可动极板连接;PLZT陶瓷在UV光照下所产生的光生电压会施加到悬臂梁自由端上的铜箔极板和基座上的铜箔极板上,从而在两个铜箔极板之间形成光致静电场,在静电力的作用下,悬臂梁会发生弯曲变形。悬臂梁的长度、宽度和厚度分别记为l、b和h;铜箔的长度为lcu,宽度为bcu,其厚度远小于悬臂梁厚度,对自由端挠度的影响可以忽略不计。
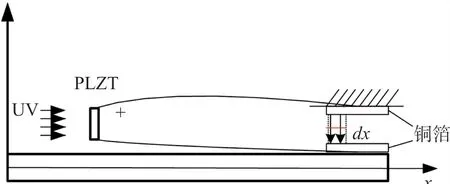
图1 光电-静电符合驱动悬臂梁示意图
如图1所示在静电力的作用下,悬臂梁在y方向发生弯曲变形,接下来分析光电-静电复合驱动悬臂梁的微元结构(如图2所示),其中d为可动铜箔极板与固定铜箔极板之间的初始间距,取一个微元dx,此微元上的挠度为dw。此时,将该微元近似看作一个平行板电容结构,间距为d-dw。

图2 光电-静电驱动悬臂梁微元示意图
则微元平行板电容结构的能量dW可表示为

式中:U是微元电容结构间的电压;dC是微元电容结构的的电容;εA是空气的介电常数。
由虚功原理,可知
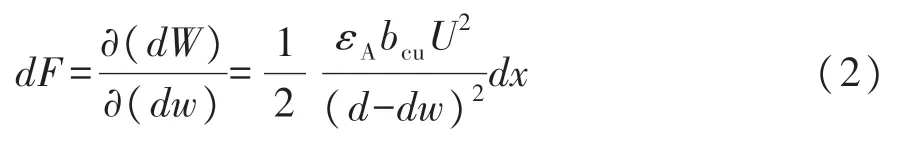
式中:dF是微元dx上两平行板之间的静电力。
图3为悬臂梁受静电力简化模型,悬臂梁受静电力时,自由端挠度wtail的表达式为

式中:a为力F的施加点到原点的距离;E为悬臂梁的弹性模量;I为悬臂梁的截面惯性矩。

图3 悬臂梁受静电力简化模型
对悬臂梁自由端而言,受到微元dx上产生的微元力dF时,悬臂梁自由端的挠度值dwtail按式(3)可以写为

将式(2)代入式(4)得到光电-静电驱动下自由端挠度微分表达式,用x代替a表示在悬臂梁上任意点所受到微元静电力的作用,再用wtail代替dw。最终得到悬臂梁自由端挠度的表达式为

式(5)表示的物理含义是在悬臂梁的x点处施加一个微元静电力dF,在悬臂梁的自由端产生一个微元挠度值dwtail。
整理式(5),即得到悬臂自由端挠度的微分方程如下

利用挠度的叠加特性对式(6)两边分别积分即可求得悬臂梁自由端的挠度解析值,可以表示为

考虑到初始条件,即当lcu=0时,悬臂梁自由端挠度w l=0;计算式(7)得到悬臂梁自由端挠度w l的解析表达式为

在光电-静电复合驱动MEMS悬臂梁机构中驱动电压是PLZT陶瓷产生的光生电压,光生电压U可由如下公式表示

式中:τ为光照时间常数;Acur为光电流响应系数;Ar为光电阻响应系数;I为光照强度;αcur为光电流随光照变化常数;αr为光电阻随光照变化常数;IP为PLZT陶瓷片产生的光电流;RP为PLZT陶瓷片的等效电阻;CP为PLZT陶瓷片的等效电容。
综上分析,悬臂梁自由端挠度将随着光照强度和光照时间而发生变化。本文将采用文献[14]中PLZT陶瓷样品进行饱和挠度分析,将文献[14]基于试验数据拟合出的αcur=0.690 8,αr=0.429 3,AcurAr=322.76,代入式(9)可得到饱和光生电压随光照强度变化的曲线如图4所示。
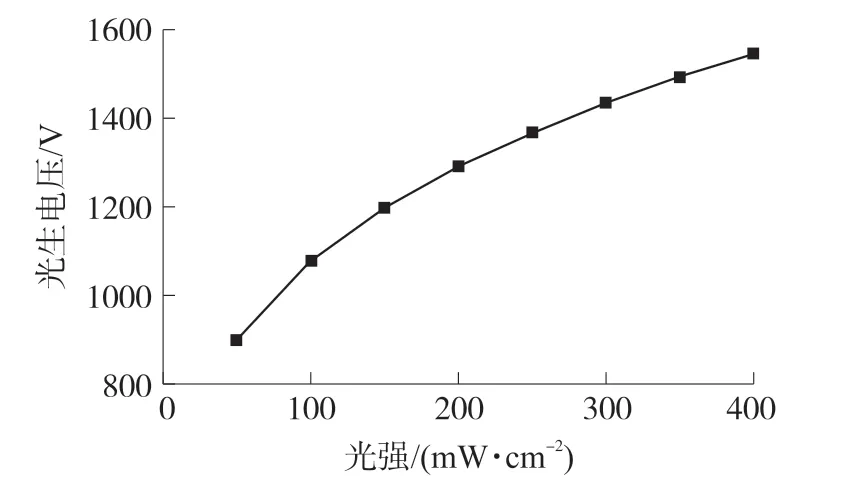
图4 光照强度与反常光生伏特效应电压关系
2 光电-静电场位置分布数学模型
在光电-静电驱动器中,光电-静电场的长度要小于悬臂梁的长度,光电-静电场与悬臂梁固定端的距离将影响悬臂梁自由端的挠度,下文构建考虑了光电-静电场区域大小及其位置分布的悬臂梁自由端挠度数学模型。如图5所示为光电-静电场在MEMS悬臂梁上的位置分布示意图。
光电-静电场区域左右两端的坐标分别为x1和x2,光电-静电场的中心位置用c表示,lcu表示静电场的长度。当光电-静电场的静电区域增大时,lcu值也随之增大;当光电-静电场沿着x轴正向不断移动时,c的值也随之增大。光电-静电场的静电区域大小和位置变化时引起悬臂梁自由端挠度的变化。

图5 光电-静电场在MEMS悬臂梁上的位置分布示意图
根据图5,得到c和lcu与x1和x2的几何关系为

对图5所示的变静电场区域位置和大小的悬臂梁机构,同样可以采用式(5)计算悬臂梁自由端挠度。将悬臂梁的静电区域分为无数个长度为dx的微元,每个微元上的静电力dF都使悬臂梁自由端产生挠度变形,利用挠度的叠加特性,可求得整个静电区域的静电力产生的自由端挠度,自由端的微元挠度满足式(5)所示的方程。此时,静电区域为[x1,x2],对式(6)的右边求定积分的时候,其积分上下限相应的变为x1和x2,积分表达式如下所示

积分后得到悬臂梁自由端挠度w l的解析表达式为
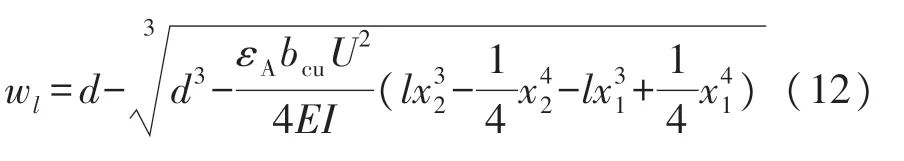
对式(12)而言,光电-静电复合驱动MEMS悬臂梁的自由端挠度w l除了与光生电压U、悬臂梁尺寸等因素有关之外,还和静电场坐标x1和x2有关,即和静电场区域的大小和位置都有关。
3 光电强度和静电场分布对悬臂梁挠度的影响及优化分析
由前述分析可知,光电-静电复合驱动MEMS悬臂梁的自由端挠度受照射PLZT陶瓷的光强大小、介电常数、悬臂梁尺寸和光电-静电场的分布影响。为了得到光电强度和静电场分布对悬臂梁挠度的影响规律,假设悬臂梁的尺寸l、b和h分别为200μm、40μm和10μm,光电-静电场的特性参数如表1所示,分别对施加在PLZT陶瓷上的光照强度、静电场分布位置和静电场区域大小对悬臂梁自由端挠度的影响规律进行研究。

表1 光电-静电场特性参数
(1)PLZT陶瓷所受光强对悬臂梁自由端挠度的影响
结合式(8)和(9)可以得到悬臂梁自由端挠度与PLZT陶瓷所受光强的关系,式(13)为PLZT陶瓷在饱和光照下的光强与悬臂梁饱和挠度的关系式

设置光电-静电场位于MEMS悬臂梁的中间位置,即c=100μm,光电-静电场的长度lcu=180μm,基于图5所示的不同光照强度下的饱和光生电压,如果PLZT陶瓷所受的高能紫外光光强从50 mW/cm2逐步增加到450 mW/cm2,得到悬臂梁自由端挠度随光电强度变化规律曲线如图6所示。由图6可以看到,悬臂梁自由端饱和挠度随着光照强度增大而增大。因此,为了获得较大驱动能力,可适当增大施加在PLZT陶瓷上的光照强度。
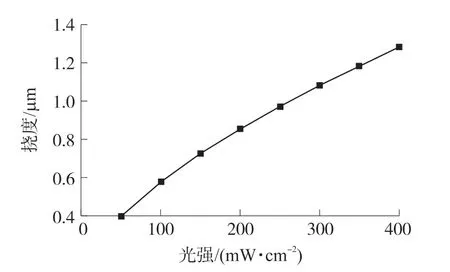
图6 悬臂梁挠度随光电强度变化的规律曲线
(2)光电-静电场分布位置对悬臂梁自由端挠度的影响
利用式(10)把x1和x2用光电-静电场参数c和lcu代替,再将其代入式(11),可以得到悬臂梁自由端挠度关于c和lcu的表达如式(14)所示

当光照强度为300 mW/cm2时驱动电压为1 434 V,光电-静电场的长度lcu=20μm,中心位置c从10μm逐渐变化到190μm,得到MEMS悬臂梁自由端的挠度变化曲线如图7所示。从图7可以看出,随着光电-静电场不断远离MEMS悬臂梁的固定端,其自由端的挠度不断增大。因此,如想要增大MEMS悬臂梁的挠度输出,应该在允许范围内,尽可能让静电区域远离悬臂梁的固定端。
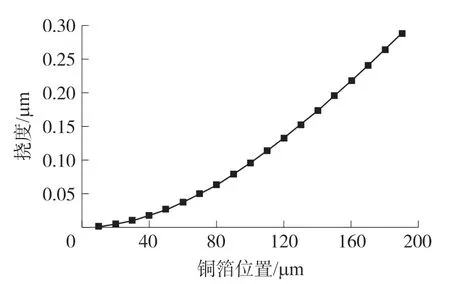
图7 悬臂梁自由端挠度随光电-静电场中心位置的变化规律
(3)光电-静电区域大小对悬臂梁自由端挠度的影响
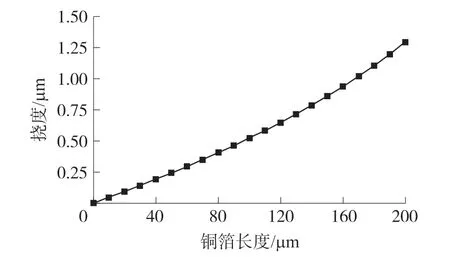
图8 悬臂梁挠度随光电-静电场长度的变化规律曲线
如让光电-静电场的位置位于MEMS悬臂梁的中间位置,即c=100μm。光照强度为300 mW/cm2,分析光电-静电区域逐渐增大(即从0μm逐渐增大到200μm)对自由端挠度的影响规律,分析结果如图8所示。从图8可以看出MEMS悬臂梁自由端的挠度随着光电-静电区域的增大而增大。
4 结束语
本文利用PLZT陶瓷在紫外光照射下的光电效应,提出一种光电-静电复合驱动MEMS悬臂梁的驱动机构,是一种无电磁干扰、非接触远程光控的新型微驱动;与常规的电磁激发类驱动方式有很大的不同。基于PLZT光生伏特效应和悬臂梁弯曲变形叠加原理建立了光电-静电复合驱动MEMS悬臂梁模型;利用平行板电容器原理,推导出微元静电力与悬臂梁微元挠度的关系表达式,进而解得悬臂梁自由端挠度的解析表达式,并分析出驱动电压随PLZT陶瓷受光照强度变化的规律;最后分析了光照强度、静电场位置和静电场大小对悬臂梁的挠度影响。仿真结果显示,悬臂梁自由端挠度与光照强度、静电场远离固定端的距离、静电场区域大小成正相关变化。因此,为了获得更大挠度输出,一方面可增大静电场区域,另一方面应尽量使静电场位置靠近悬臂梁的自由端。

