高速列车底板铆钉结构的分区应力解算与气动疲劳评估

周 伟，李佳乐，王兆华，付少青，王维峰

(1.中南大学 轨道交通安全教育部重点实验室，湖南 长沙 410075；2.中车青岛四方机车车辆股份有限公司，山东 青岛 266111)

高速铁路是中国的一张亮丽名片，随着列车运行速度的提高，气动载荷对车体结构的影响也更加显著，疲劳破坏等问题日益突出，因此开展疲劳评估的研究具有重要意义[1，2]。气动载荷的研究为解决高速列车结构的气动疲劳问题提供了理论依据，Baker等[3]通过风洞试验测量车辆的多点历史压力值进而确定车辆上的复杂脉动压力场。Fujii等[4]采用数值仿真的方法研究了列车交会时的相互气动作用和产生的流场的基本特征。Niu等[5]对不同编组长度的列车以各自最不利长度隧道通过和交会工况进行模拟，并对车体表面产生的交变压力载荷进行研究。聚焦列车风挡、车体与设备舱结构等；针对风挡结构，刘珍[6]对高速列车橡胶外风挡下部出现的裂纹现象进行流体力学仿真分析，将其归因于列车交会产生的气动载荷；针对车体结构，Lu等[7]首次采用顺序耦合方法研究压力波对大型复杂车体结构疲劳强度的影响，并发现短隧道气动载荷对疲劳强度的安全系数比长隧道低15%，权海阳[8]研究了时速400 km下的高速列车车体气动载荷及气动载荷谱，王前选等[9]研制了车体交变气动载荷试验装置以实现车体结构的气动疲劳加载，张德文[10]研究了列车隧道会车时气动载荷对车体的影响，宋烨等[11]研究了明线会车、隧道通过、隧道会车和侧风4种气动载荷工况下车体的疲劳强度，Miao等[12]研究了侧风作用下高速列车车体非定常的空气动力载荷；针对设备舱结构，段华东等[13]分析里了气动载荷对设备舱的影响并优化了设备舱结构，黄珊[14]采用数值仿真与实车试验相结合的方法研究了气动载荷对设备舱的影响，刘业博[15]采用不同的流体仿真方法，编制了单车明线运行、单车过隧道和明线交会工况下的设备舱气动载荷谱，并评估了设备舱裙板结构的疲劳损伤，Zhou等[16]采用雨流计数建立了八级载荷谱以研究设备舱的基体金属与焊缝的疲劳特性。由此可见，国内外学者通常采用仿真与试验的方法解决气动载荷导致的列车疲劳问题，针对列车底板铆钉结构的气动载荷疲劳研究仍处于相对空白的状态。

高速列车底板结构作为设备舱底部的关键密封板，在列车高速通过隧道或交会时，会承受强交变、大幅值气动载荷作用。铆接件的铆孔结构存在较为严重的应力集中，长期受到循环交变载荷作用，这些区域极易出现裂纹、甚至出现疲劳失效发生脱落，严重时导致底板结构脱落，影响列车运行安全。本文以高速列车底板为研究对象，通过实车试验获取真实气动载荷谱，基于有限元仿真、雨流计数法与累积损伤准则，建立铆钉结构件的疲劳损伤评估模型，为底板铆钉结构的疲劳损伤评估和优化提供科学依据。

1 分区加载有限元应力解算

1.1 模型描述

本文研究对象为某型高速动车组牵引变流器主风机安装底板结构，底板结构通过两侧各3个抽芯铆钉与车体底部骨架横梁连接在一起，如图1(a)所示。其中，底板厚度为1.5 mm，骨架横梁厚度为5 mm、长度取1 018 mm(与底板同)，铆钉结构公称直径为4.8 mm，底板、骨架梁与铆钉结构的材料参数如表1所示。

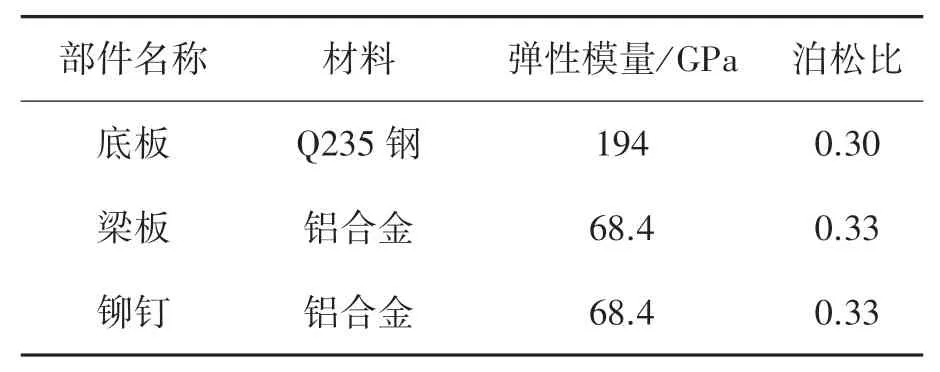
表1 材料参数定义

采用六面体结构网格对铆钉、底板和骨架梁结构进行离散，并对接触区域进行网格加密处理，共生成六面体实体单元86 580个、节点112 103个，底板-铆钉-骨架梁耦合有限元模型如图1(b)所示，三者之间的相互接触对定义如图1(c)所示。其中，接触对的摩擦系数取0.17[17]。根据铆钉的拉伸极限强度试验[18]，钉芯的拉断力为1 000 N，故铆钉预紧力取1 000 N。

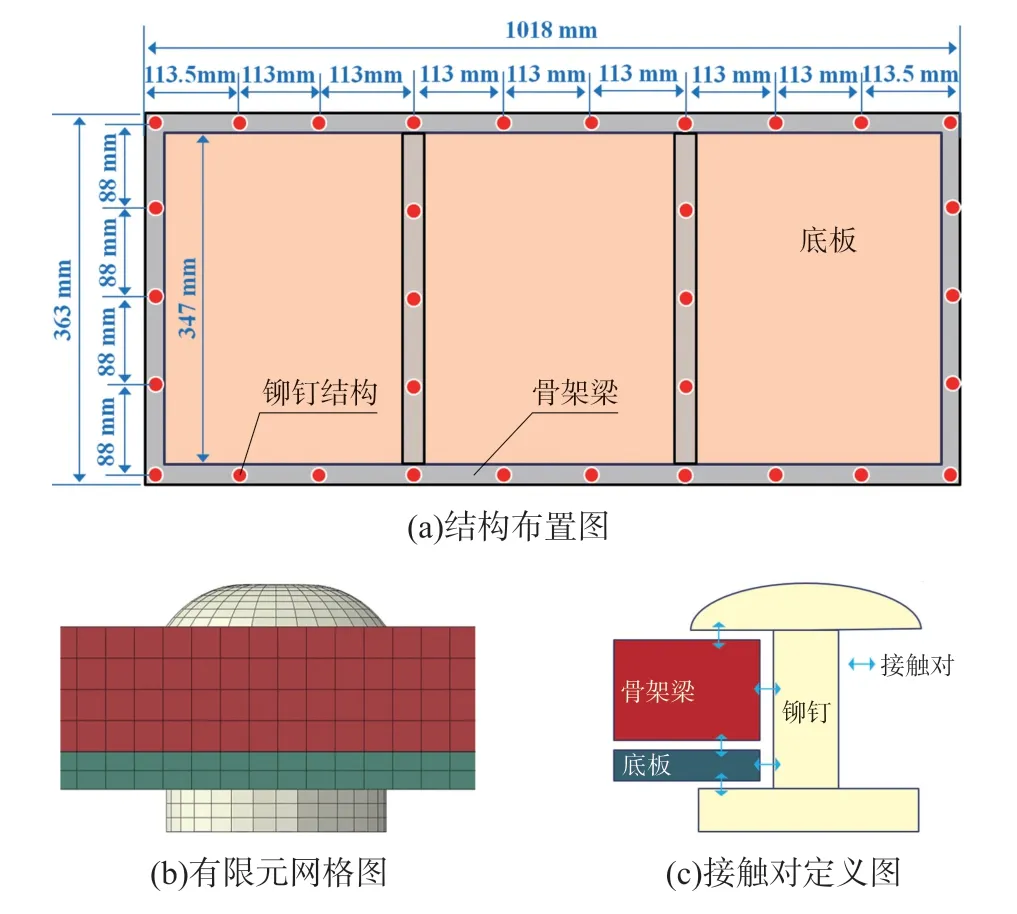
图1 底板-铆钉-骨架梁耦合分析模型

1.2 分区解算

由于底板结构沿车宽方向受到不均匀分布的气动载荷，为准确分析结构应力分布，风机安装底板被骨架梁分为1＃、2＃、3＃这3个子区域，分别在3个子区域单独施加不同幅值气动载荷P1、P2、P3，确定所有32个铆钉件的大值应力点，各区域的铆钉结构危险点分别定义为P、S、Q(分别为2取1)，建立线弹性阶段铆钉结构应力与分区气动载荷的传递系数，如图2所示。

采用加权计损的方法，对每个子区域单独仿真，确定各子区域气动载荷对铆钉结构的应力贡献权重，通过权重系数把结构应力解算出来，完成结构疲劳损伤评估。

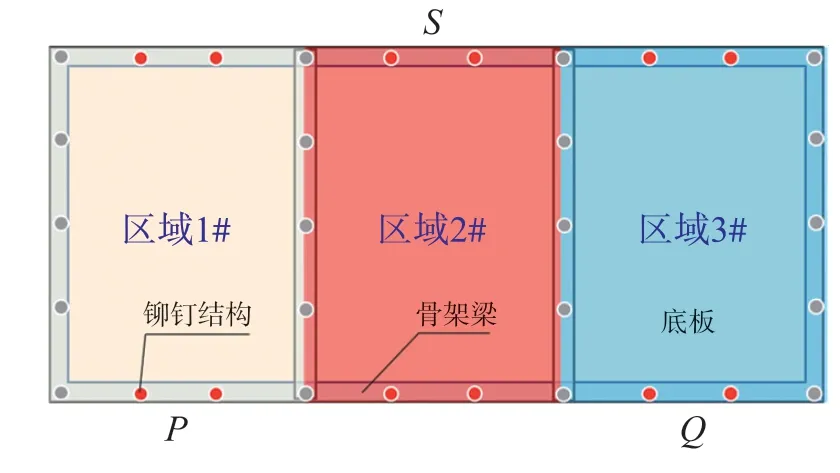
图2 铆钉危险点P、S、Q

当在1＃区域单独施加气动载荷P1时，得到气动载荷P1与铆钉各危险点的六分量应力的传递系数分别为C1XX、C1YY、C1ZZ、C1XY、C1YZ、C1ZX；在2＃区域单独施加气动载荷P2时，得到气动载荷P2与铆钉各危险点的六分量应力的传递系数分别为C2XX、C2YY、C2ZZ、C2XY、C2YZ、C2ZX；在3＃区域单独施加气动载荷P3时，得到气动载荷P3与铆钉各危险点的六分量应力的传递系数分别为C3XX、C3YY、C3ZZ、C3XY、C3YZ、C3ZX。记当前实测3个区域的气动载荷分别为P1test、P2test、P3test，则各区域危险点的六分量应力SXX、SYY、SZZ、SXY、SYZ、SXZ解算模型如式(1)所示

式中:i表示铆钉危险点位置P、S、Q；S0XX～S0ZX为铆钉预紧力(1 000 N)作用下铆钉危险点的六分量静应力。对危险点P分别取值为15.0 MPa、41.8 MPa、100.9 MPa、6.6 MPa、16.8 MPa和-6.5 MPa，对危险点S分别取值为7.1MPa、39.5 MPa、110.1 MPa、6.1 MPa、23.0 MPa和-6.7 MPa，对危险点Q分别取值为15.0 MPa、40.2 MPa、103.4 MPa、6.4 MPa、16.1 MPa和-6.4 MPa。

根据实测气动载荷的极值(-200～400 Pa，正压表示自内而外)，以50 Pa为增量计算铆钉结构应力，得到铆钉结构P、S、Q点的六分量应力与气动载荷的重构系数如表2。

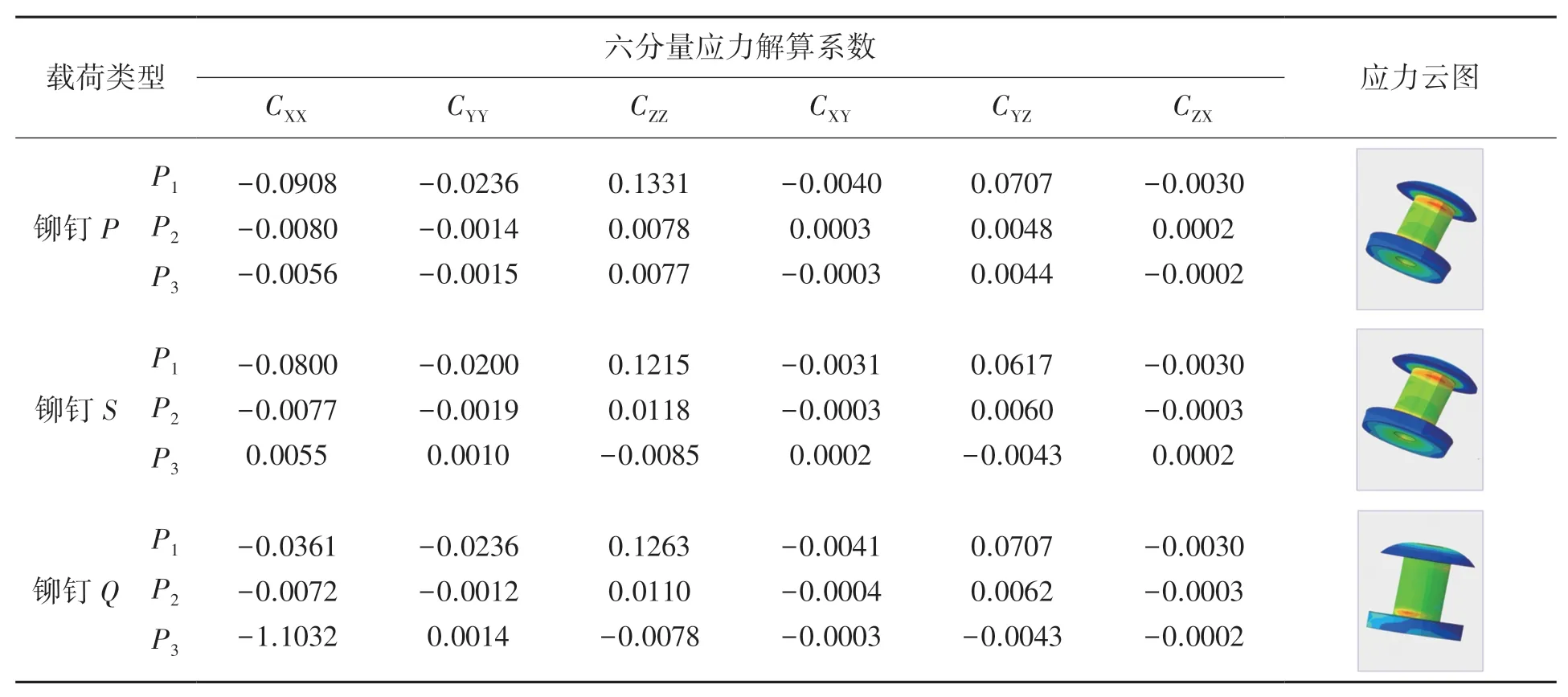
表2 六分量应力传递系数解算结果 MPa/Pa

2 气动载荷试验研究

2.1 试验概况

对武广客运专线上运行的某型动车组牵引变流器主风机安装底板的沿车长方向前、中、后3个区域的中心位置布置3个差压传感器测点。底板内外气动差压的外部压力采用薄圆形感压片设置在测点位置；内部压力通过导压软管过盈连接贯通小孔至测点位置底板内部，测点分布位置如图3所示。

图3 底板3处气动差动压力测点位置

由于武广客运专线沿线地形复杂，海拔高度差较大，会引起测点压力大范围变化与差压测量精度之间的矛盾，因此采用基于薄元介质感压的差压双向同步导压测量方法，即前端双薄元感压片进行气动压力的感知，中间有限长度导压软管进行气压传递，后端双向差压输入进行气动差压同步测量。采用网络传输采集设备进行数据采集，并通过LabVIEW编写数据分析程序。

2.2 载荷谱编制

根据应力传递因子和载荷-时间历程曲线，可以得到不同时刻的铆钉结构应力，即应力时程曲线。实车试验3个测点的气动载荷值-时间历程曲线如图4所示。

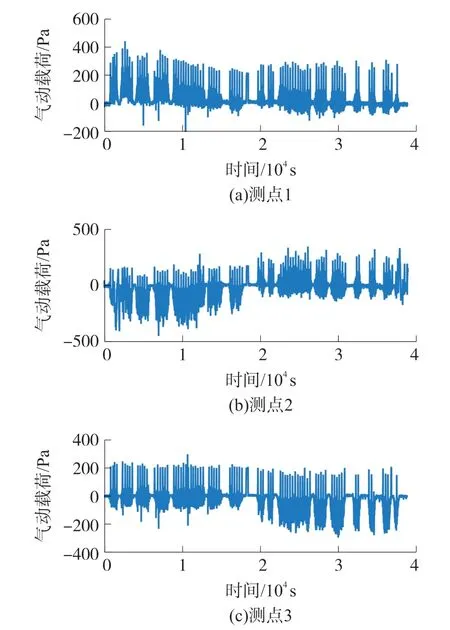
图4 气动载荷-时间历程曲线

通过实车试验测得各测点气动载荷时程，代入应力解算式(1)得到铆钉危险点P、S、Q的六分量应力SXX、SYY、SZZ、SXY、SYZ、SXZ，通过结合第四强度等效应力，Von Mises应力计算方式如式(2)所示

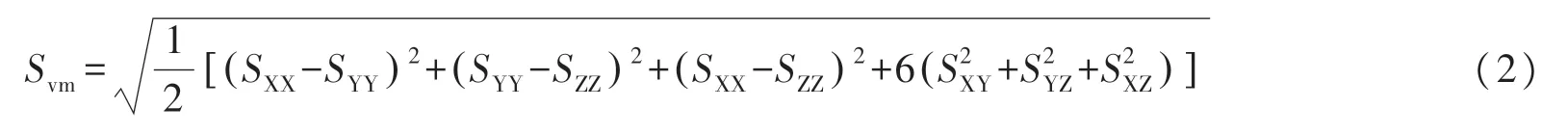
由于Von Mises应力为非负应力值，没有考虑载荷对称循环性，因此在疲劳分析中考虑带符号的Von Mises结构应力，其计算方法如式(3)所示

式中:sign函数为取变量正负符号函数；I1是第一应力不变量，I1=SXX＋SYY＋SZZ。

当气动载荷分别作用于底板区域1＃、区域2＃和区域3＃时，通过结构六分量应力解算矩阵(1)、带符号等效应力式(2)和(3)，获取铆钉结构3处危险点P、S、Q的等效应力时程如图5所示。

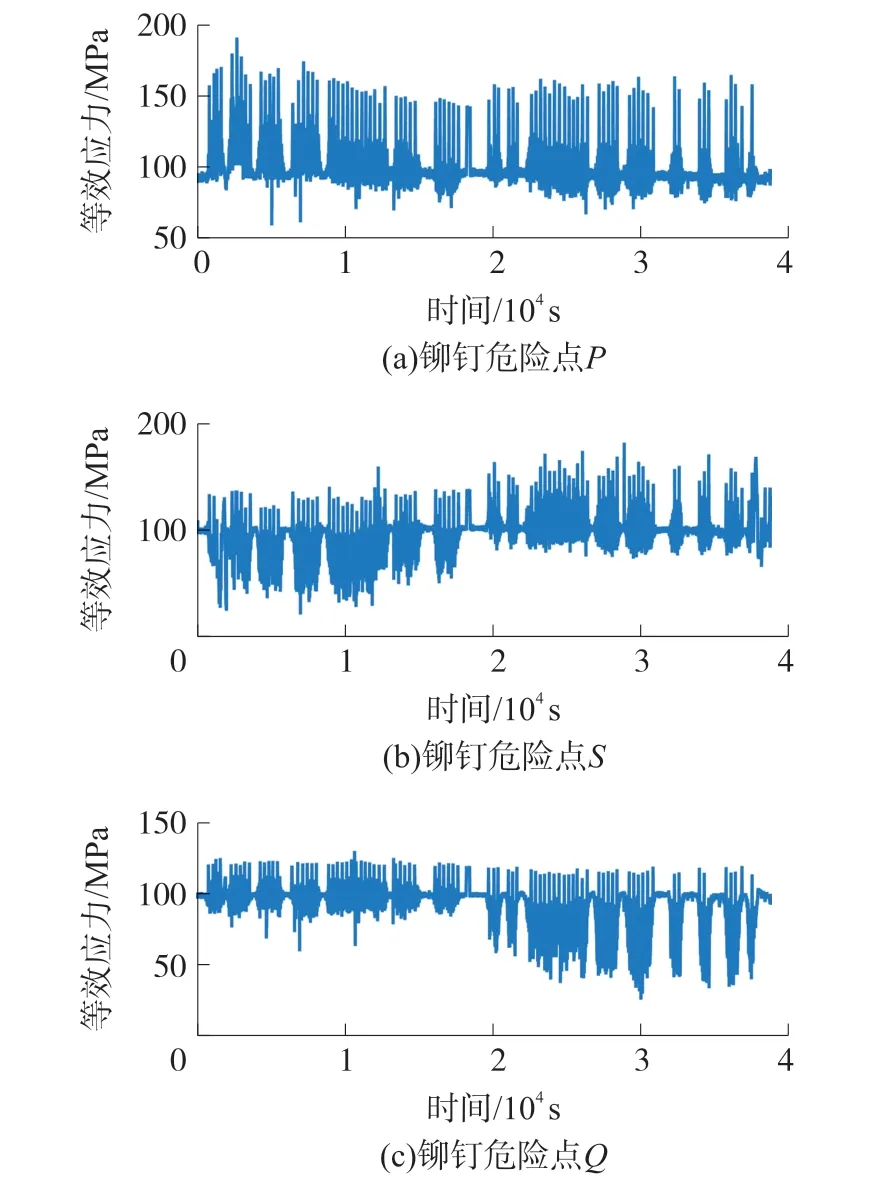
图5 铆钉结构等效应力时程解算

由于各危险点等效应力为拉应力，考虑载荷均值对幅值的损伤贡献，采用雨流计数法统计结构二维应力均幅值的八级载荷谱，并通过64级三维柱状等值云图展现各级载荷循环频次在8级区间的分布，如图6所示。由图6可以看出，铆钉结构3处危险点P、S、Q的应力均值分布不同，P点应力均值主要分布在83～105 MPa，S点应力均值主要分布在73～107 MPa，Q点应力均值主要分布在85～108 MPa，P点所在分区应力幅值变化较大。铆钉结构3处危险点P、S、Q的应力均值波动中心不同，P点在83～160 MPa之间，S点在38～158 MPa之间，Q点在85～166 MPa之间。

图6 铆钉结构二维应力均幅值载荷谱

3 疲劳损伤评估

3.1 材料疲劳参数

为了对结构进行准确的疲劳损伤评估，必须建立外部载荷与结构寿命之间的关系。取横坐标为疲劳载荷循环次数N，纵坐标为试件的疲劳强度S，便得到材料的S-N曲线。该曲线包含有限疲劳寿命阶段和无限疲劳寿命阶段。在有限疲劳寿命阶段，交变应力作用下构件达到一定循环次数就会发生疲劳破坏；在无限疲劳寿命阶段，如果应力低于临界点应力，则无论应力循环多少次，都不会发生疲劳破坏，故临界点对应疲劳极限循环次数，本文取1×107次。

铆钉、底板与骨架结构的材料疲劳参数[19，20]如表3所示。

表3 疲劳参数定义

3.2 累积损伤理论

根据S-N曲线定义的循环应力载荷幅[21，22]，当达到结构的疲劳极限循环次数N时将产生疲劳失效，但当结构的循环次数n未达到极限循环次数N，j为应力水平级数，则在不同的应力水平下，都将产生一个损伤率n i/N i，其中n i为第i级的应力水平级数，Ni为第i级应力水平的疲劳寿命。当这些在不同的应力水平下产生的损伤率加在一起达到1时，就会出现完全失效[23]。Miner线性累计损伤理论因简便、准确而得到了广泛的应用。根据Miner线性累积损伤理论，其过程可表示为

当疲劳总损伤D=1时，即认为疲劳失效。

对应力载荷进行处理编制二维八级载荷谱，结合材料的疲劳参数和Miner准则计算疲劳损伤。疲劳计算应当首先确定材料的S-N曲线方程

式中:Sa为应力幅值；m、C为材料S-N曲线参数。对Q235钢材[24]，m=7.829，C=1.0×1024.08；对A6N01S铝合金[19]，m=9.9529，C=3.32×1026。

第i级载荷幅为Sai，循环次数为C i时的疲劳损伤为

式中:Ni为第i级载荷幅对应的疲劳极限循环数。

根据式(5)和(6)，在第i级载荷幅值下的疲劳损伤为

式中:Sai为i级载荷水平下的幅值。

二维载荷谱区别于仅考虑载荷幅值的一维载荷谱，考虑载荷幅值和均值对疲劳的影响，因此采用Goodman修正后的等效对称循环应力[25]，其计算公式为

式中:S-1为对称循环载荷幅值，Sa为载荷幅值，Sm为载荷均值，Su为极限强度。

因此二维八级载荷谱下，根据S-N曲线可计算载荷循环次数为N ij时对应的疲劳损伤D ij，总损失D计算如下

动车组单日运行里程记为LC，气动载荷导致疲劳损伤记为DC，高速动车组设计服役寿命为S(运行里程)，则结构当量损伤DEQV定义为车辆达到设计寿命时的累积损伤，如式(10)所示

若DEQV＜1，则认为铆钉结构在动车组设计寿命内满足使用要求；反之，则认为铆钉结构会发生疲劳破坏。

3.3 损伤评估分析

高速动车组的设计寿命为1 200万千米，将日运行2 100 km的载荷循环次数等效至设计寿命，并计算各级应力均幅值下的当量损伤，得到铆钉结构危险点P、S、Q的总当量损伤与安全系数，如表4所示(安全系数为容许损伤1.0除以当量损伤)。

表4 运行里程1 200万千米当量损伤与安全系数

从疲劳当量损伤的对比结果来看，S点铆钉结构的当量损伤最大，当运行里程达到设计寿命时，其损伤达0.83，安全系数为1.20；其他两个铆钉危险点的当量损伤均在0.34以上；因此，高速动车组在具有隧道群的武广铁路运行时，复杂环境下动车组服役1 200万千米的设计里程，铆钉能够满足使用要求，但安全系数较低，仅为1.20。

从底板铆钉结构的重构应力响应来看，其初始结构应力较大，达100 MPa，交变气动载荷造成的动应力变化幅值也达80 MPa，因此建议从铆钉规格选取上提升铆钉强度，满足连接可靠性前提下优化初始拉铆力以降低其初始静应力，合理设计骨架梁与铆钉的对称布置形式以平滑集中应力，通过以上措施提升铆钉结构的服役性能。

4 结束语

(1)本文针对高速列车风机安装底板铆钉结构的气动疲劳问题，提出底板/铆钉/骨架梁耦合分区气动加载的应力有限元解算模型，通过对每个子区域分区加载，明确各子区域气动载荷对铆钉结构的应力贡献权重，建立了底板弯曲效应下铆钉结构的等效应力重构模型。

(2)通过对武广铁路高速列车日运行2 100 km的线路气动载荷进行跟踪实测，获取动车组变流器主风机安装底板的分区气动载荷谱，以此重构危险点铆钉结构的等效应力谱，采用雨流计数与累积损伤准则进行二维疲劳损伤评估。当高速列车运行里程达设计里程时，危险点铆钉结构的最大当量损伤达0.83，满足使用要求，但安全系数较小。

(3)为降低铆钉结构初始静应力和动应力幅值，建议从铆钉规格选取、初始拉铆力设计和骨架梁-铆钉几何布置优化出发，以提升铆钉强度、降低初始应力、平滑集中应力，从而提升铆钉结构的服役性能，确保行车安全。