GI/G/1排队系统的近似分析

赵 宁，黄小峰，刘文奇

(昆明理工大学1.数据科学研究中心；2.理学院，云南 昆明 650500)

现实生活中存在各种各样的随机服务系统，排队论是分析和优化随机服务系统性能的有效工具[1，2]。本文针对到达过程是一般过程，服务时间服从一般分布的GI/G/1排队系统展开研究，以便为解决诸多实际问题提供理论依据。

经典的单一服务器的排队系统已经被广泛研究，例如M/M/1排队系统、M/G/1排队系统、GI/M/1排队系统等。M/M/1排队系统可以通过分析相应的马尔可夫过程求解系统的性能指标(队长的概率分布、逗留时间分布、忙期等)。关于M/G/1排队系统，可以通过在顾客离去时刻构造嵌入马尔可夫链，得到排队系统的平均等待时间[3]。对于GI/M/1排队系统，可以在顾客的到达时刻构造嵌入马尔可夫链，运用到达过程的Laplace-Stieltjes变换得到GI/M/1排队系统平均等待时间的解析表达式[3]。

GI/G/1排队系统通常不具有马尔可夫性，理论上无法求解系统性能指标的解析表达式，以往关于这一系统的研究主要是近似分析。近似分析方法包括两类:扩散近似和启发式近似。Kobayashi[4]运用高斯过程及其扩散方程，研究了GI/G/1排队系统及一般排队网络中队长的近似概率分布。Heyman[5]通过构造近似扩散过程，得到了GI/G/1排队系统的等待时间和队长分布。Krämer和Langenbach-Belz[6]使用启发式方法提出了平均等待时间和等待概率的近似表达式。Gelenbe[7]使用不同的扩散近似模型研究了GI/G/1排队系统平均等待时间的近似。Marchal[8]提出使用到达时间间隔和服务时间分布的一阶矩、二阶矩相关的近似公式分析一般单服务器排队系统的平均等待时间。

二阶近似在到达时间间隔变化较大时很难获得较好的近似值，在这种情况下，三阶矩对GI/G/1排队系统的平均等待时间有显著的影响。Myskja[9，10]基于H2/M/1排队系统的精确结果，根据到达时间间隔的一阶至三阶矩和服务时间的一阶、二阶矩，提出了GI/G/1排队系统平均等待时间的启发式近似。Myskja[10]指出，如果到达时间间隔不服从H2分布，这种三阶近似方法表现不佳。为此，Wu等[11]引进服务时间和到达时间间隔的三阶矩，对GI/G/1排队系统平均等待时间的近似方法进行了改进。虽然Wu等[11]利用三阶矩的启发式近似方法提高了近似的精度，却无法分析系统的队长概率分布。

由于GI/G/1排队系统通常不具有马尔可夫性，理论上无法精确求解，本文试图将到达时间间隔和服务时间近似为满足马尔可夫性的随机变量，从而对系统进行近似分析。如果给定随机变量的一阶至三阶矩，Bobbio等[12]提出可以用非周期的相位(Phase type，PH)分布拟合一般分布，Osogami和Harchol-Balter[13]提出了用PH拟合任意分布的算法。此外，通过PH分布，可以构造马尔可夫到达过程(Markovian arrival process，MAP)。

MAP和PH分布具有马尔可夫性，被广泛用于排队系统的研究。Sreenivasan等[14]研究了具有休假的MAP/PH/1排队系统。Zhao等[15]研究了具有两类顾客和自主优先权的MAP/PH/1排队系统。Brugno等[16]研究了具有批量服务的MAP/PH/1排队系统。Ye等[17]研究了具有休假和有限缓冲区的离散时间MAP/PH/1排队系统，得到了系统队长的稳态概率分布以及损失概率等性能指标。但是目前尚未有学者详细分析MAP/PH/1排队系统对GI/G/1排队系统的逼近效果。

本文将GI/G/1排队系统通过近似方法构建为MAP/PH/1排队系统，根据排队系统相邻到达时间间隔的一阶至三阶矩将到达过程近似为MAP，根据服务时间的一阶至三阶矩将其近似为PH分布。利用矩阵几何解的方法分析相应的MAP/PH/1排队系统，得到GI/G/1排队系统性能指标的近似解，并将本文提出的方法与现有的近似方法进行误差分析。

1 GI/G/1排队系统描述

本文研究具有一般性的单服务器排队系统——GI/G/1排队系统。这一系统中相邻顾客到达时间间隔XG独立且服从一般分布，服务时间SG也是独立同分布的，XG和SG相互独立。假设XG和SG的i阶矩存在，分别记为和，i=1，2，3。XG和SG的平方变异系数分别是，，且

系统缓冲区无限大，按照先到先服务的规则服务。假设系统的到达率为λ，，服务速率为μ，，服务强度ρ=λ/μ，且ρ＜1。

2 GI/G/1排队系统的近似分析方法

本节将GI/G/1排队系统的到达过程近似为MAP，服务时间近似为PH分布，将GI/G/1排队系统近似为MAP/PH/1排队系统。通过分析相应的MAP/PH/1排队系统，得到GI/G/1排队系统性能指标的近似解。

2.1 服务时间的近似

首先根据服务时间SG的i阶矩(i=1，2，3)，将其分布近似为PH分布，记为(β，T)，其中β为1×n向量，T为n×n矩阵。服从PH分布的服务时间SPH的i阶矩为[18]

式中:e为所有元素都为1的列向量。

构造(β，T)的基本原则是SPH的一阶至三阶矩分别与SG的一阶至三阶矩相等，即

将E k-1，k(α)表示为PH分布的形式(β，T)如下

将H2(p1，p2；α1，α2)表示为PH分布的形式(β，T)如下

通过求解上述方程组，可得p1，p2，α1，α2，从而得到服务时间的近似PH分布(β，T)。

2.2 到达过程的近似

根据到达时间间隔XG的i阶矩(i=1，2，3)，构造马尔可夫到达过程(D0，D1)，其中D0和D1是m×m矩阵，D0表示没有顾客到达的情况下MAP的状态转移速率矩阵，D1表示有顾客到达的情况下MAP的状态转移速率矩阵。到达时间间隔XMAP的i阶矩为[19]

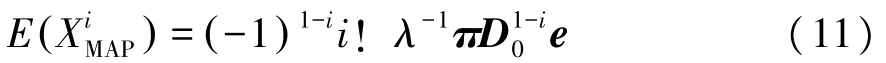
式中:λ=πD1e，π(D0＋D1)e=0，πe=1。

构造(D0，D1)的基本原则是XMAP的i阶矩与XG的i阶矩相等(i=1，2，3)，即

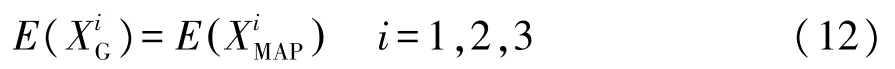
MAP的构造方法可以通过先构造满足上述条件的PH分布随机变量XPH，再由PH分布构造MAP。下面分别针对和两种情况构造MAP。

令D0=T，D1=-Teβ，则(D0，D1)即为到达过程的MAP近似。

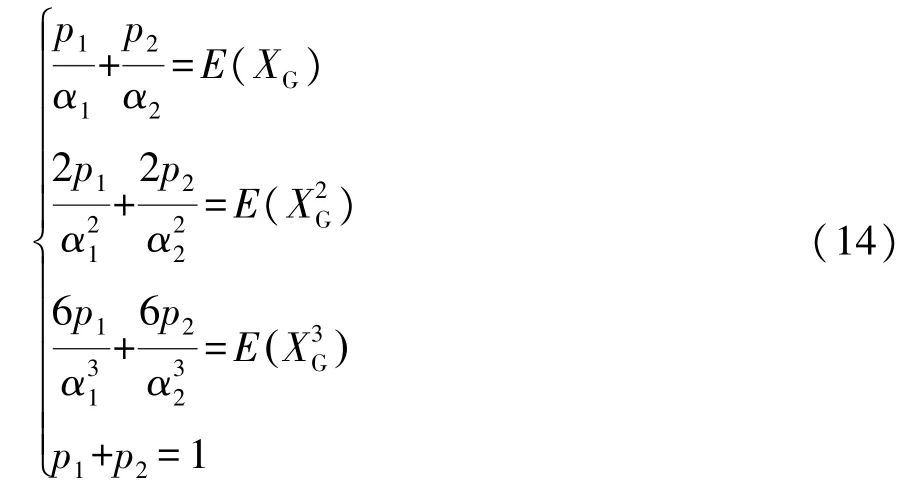
通过求解上述方程组，可得p1，p2，α1，α2，从而得到到达时间间隔的近似PH分布(β，T)。令D0=T，D1=-Teβ，则即为到达过程的MAP近似。

2.3 近似稳态概率分布

由2.1节和2.2节的方法，可以将GI/G/1排队系统近似为MAP/PH/1排队系统。MAP/PH/1排队系统可以表示为一个连续时间的三维马尔可夫过程Z(t)={N(t)，J(t)，K(t)，t≥0}，其中N(t)为t时刻系统的顾客数，J(t)为t时刻MAP(D0，D1)的状态，K(t)为t时刻服务时间PH分布的状态。

马尔可夫过程Z(t)的生成矩阵Q为

式中

式中:⊗表示Kronecker积，⊕表示Kronecker和。

Q是一个无穷行、无穷列的三对角矩阵，此马氏链可以通过矩阵几何解的方法计算稳态概率分布Π=(x0，x1，…)。

Π由ΠQ=0和Πe=1唯一确定，x0为1×m向量，x i为1×mn向量(i≥1)，表示系统里有i个顾客的概率向量，x i有以下的矩阵几何结构

R满足

通过求解以下方程组，可以得到x0和x1

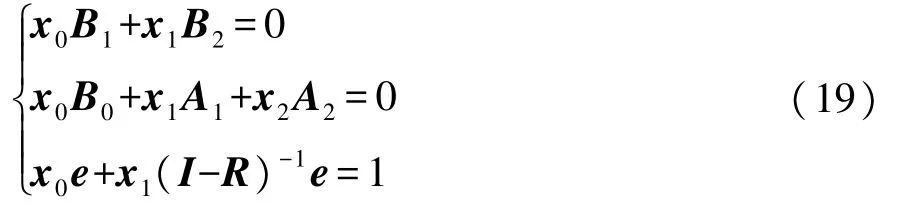
因此，GI/G/1排队系统的近似稳态概率分布为Π=(x0，x1，…)。

2.4 性能指标

由GI/G/1排队系统的近似稳态概率分布，可得如下性能指标:

(1)平均顾客数:E(L)=x1e＋2x2e＋3x3e＋…=x1(I-R)-2e；

(2)平均逗留时间:E(T)=E(L)/λ=x1(IR)-2e/λ；

(3)平均等待时间:E(W)=E(L)/λ-E(SPH)=x1(I-R)-2e/λ-1/μ。

3 平均等待时间的近似方法

关于GI/G/1排队系统的近似分析方法较多，本节总结了目前常用的GI/G/1排队系统平均等待时间的近似方法，依次记为方法1，方法2，…，方法7，将本文提出的方法记为方法8，如表1所示。

表1 GI/G/1排队系统平均等待时间的近似方法

续表1

4 数值试验

下面通过数值试验介绍怎样使用本文提出的近似方法分析GI/G/1排队系统的性能指标，并且验证其准确性。4.1节通过实例介绍一个GI/G/1排队系统如何近似为MAP/PH/1排队系统及其近似分析的效果，4.2节将本文提出的方法与现有的近似方法进行误差分析，比较各近似方法的误差大小。

4.1 实例分析

假设GI/G/1排队系统的到达时间间隔分布和服务时间分布分别为XG～Gamma(1/5，6/500)，SG～Gamma(10/7，1/7)，即E(XG)=100/6，E(SG)=10，=5，=0.7，ρ=0.6。

根据第2节的方法(见式(14))，将到达时间间隔XG近似为超指数分布，从而得到到达过程MAP(D0，D1)，且

根据(7)式将服务时间近似为PH分布(β，T)

通过矩阵几何解的方法(方法8)可求解系统队长的概率分布如图1所示，MAP/PH/1的平均等待时间的近似值为=54.454 4。

图1 队长的概率分布

对这个系统进行仿真试验，统计6×107个顾客的平均等待时间，得到平均排队时间模拟值ˉW=52.170 3。因此，近似值与模拟值的相对误差为

为了更直观地观察方法1—方法8的近似误差，图2给出了SG～Gamma(10/7，1/7)，XG～Gamma(1/5，ρ/50)，ρ∈{0.1，0.2，…，0.9}的情况下各种近似方法相对误差。图2显示方法1、2、5相对其他方法误差较大；除了方法7，其他方法的相对误差随着ρ的增大而逐渐减小。

图2 平均排队时间相对误差比较

4.2 近似方法比较

本文采用平均排队时间的平均相对百分比误差R作为评价各种近似方法准确性的指标。

以上任意情形下，当ρ取某确定值时，

E(SG)、和这3个参数有108种组合，即N=108。对任意的参数组合i∈{1，2，…，108}，根据表1计算平均排队时间近似值，与模拟值比较，从而得到方法1—方法8的平均排队时间的平均相对百分比误差。情形1—情形4的误差比较的结果分别如表2—表5所示，其中下划线“ ”表示对于某个ρ，所有方法中的最小平均相对百分比误差，例如表2中，当ρ=0.9时，方法8的平均相对百分比误差为R=0.27%。

表2—表5的数据显示:

(1)除了方法4和方法7，其他方法的平均相对百分比误差整体上随着服务强度ρ的增大而减小(见表2—表5)；

(2)启发式的近似方法(方法6—方法8)整体上优于基于扩散方程的近似方法(方法1-方法3)(见表2—表5)；

(7)当服务强度ρ较大(ρ→1)时，方法8误差最小(见表2—表5)。

综上可见，本文提出的方法8在以上4种情形下均表现较优，当或ρ→1时，方法8近似效果最好。虽然方法6和方法7在的情况下估计效果较好，但是无法估计系统队长的概率分布，方法8可以弥补方法6和方法7的不足。

表2 0＜＜1，0＜＜1时平均排队时间的平均相对百分比误差比较

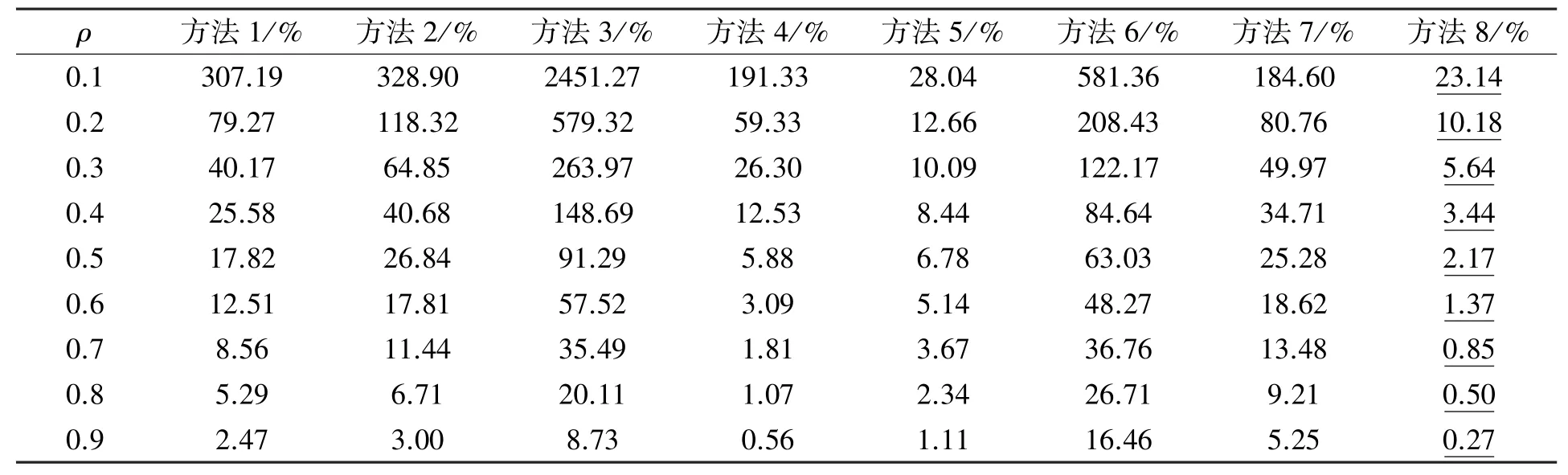
表2 0＜＜1，0＜＜1时平均排队时间的平均相对百分比误差比较

ρ 方法1/% 方法2/% 方法3/% 方法4/% 方法5/% 方法6/% 方法7/% 方法8/%0.1 307.19 328.90 2451.27 191.33 28.04 581.36 184.60 23.14 0.2 79.27 118.32 579.32 59.33 12.66 208.43 80.76 10.18 0.3 40.17 64.85 263.97 26.30 10.09 122.17 49.97 5.64 0.4 25.58 40.68 148.69 12.53 8.44 84.64 34.71 3.44 0.5 17.82 26.84 91.29 5.88 6.78 63.03 25.28 2.17 0.6 12.51 17.81 57.52 3.09 5.14 48.27 18.62 1.37 0.7 8.56 11.44 35.49 1.81 3.67 36.76 13.48 0.85 0.8 5.29 6.71 20.11 1.07 2.34 26.71 9.21 0.50 0.9 2.47 3.00 8.73 0.56 1.11 16.46 5.25 0.27

表3 0＜＜1，≥1时平均排队时间的平均相对百分比误差比较

表3 0＜＜1，≥1时平均排队时间的平均相对百分比误差比较

ρ 方法1/% 方法2/% 方法3/% 方法4/% 方法5/% 方法6/% 方法7/% 方法8/%0.1 1109.13 59.90 1362.11 10.91 20.04 79.23 18.51 4.86 0.2 395.43 26.51 483.45 16.25 12.06 31.73 2.99 2.42 0.3 212.07 15.61 259.02 14.35 7.88 18.73 0.75 1.49 0.4 130.27 10.12 159.13 10.85 5.39 12.66 1.79 0.98 0.5 84.39 6.81 103.15 7.63 3.75 9.02 2.23 0.67 0.6 55.14 4.58 67.45 5.10 2.58 6.47 2.24 0.45 0.7 34.87 2.93 42.70 3.23 1.67 4.54 1.93 0.27 0.8 20.15 1.76 24.70 1.77 1.03 2.82 1.50 0.26 0.9 8.95 0.94 10.97 0.76 0.66 1.39 0.98 0.45

表4 ≥1，0＜＜1时平均排队时间的平均相对百分比误差比较

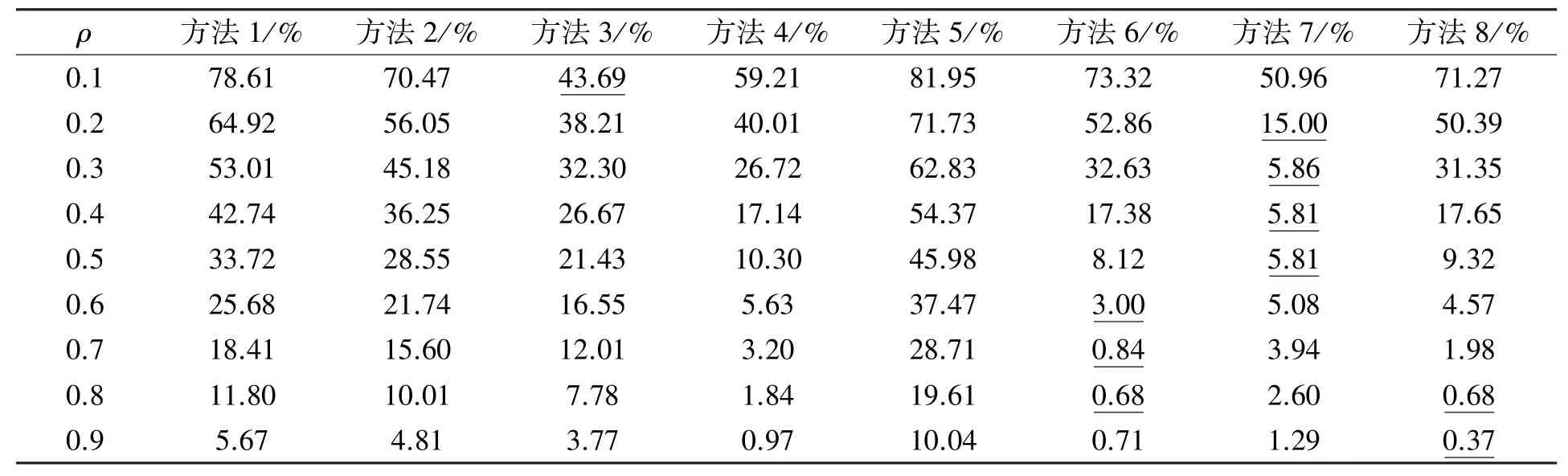
表4 ≥1，0＜＜1时平均排队时间的平均相对百分比误差比较

ρ 方法1/% 方法2/% 方法3/% 方法4/% 方法5/% 方法6/% 方法7/% 方法8/%0.1 78.61 70.47 43.69 59.21 81.95 73.32 50.96 71.27 0.2 64.92 56.05 38.21 40.01 71.73 52.86 15.00 50.39 0.3 53.01 45.18 32.30 26.72 62.83 32.63 5.86 31.35 0.4 42.74 36.25 26.67 17.14 54.37 17.38 5.81 17.65 0.5 33.72 28.55 21.43 10.30 45.98 8.12 5.81 9.32 0.6 25.68 21.74 16.55 5.63 37.47 3.00 5.08 4.57 0.7 18.41 15.60 12.01 3.20 28.71 0.84 3.94 1.98 0.8 11.80 10.01 7.78 1.84 19.61 0.68 2.60 0.68 0.9 5.67 4.81 3.77 0.97 10.04 0.71 1.29 0.37

表5 ≥1，≥1时平均排队时间的平均相对百分比误差比较

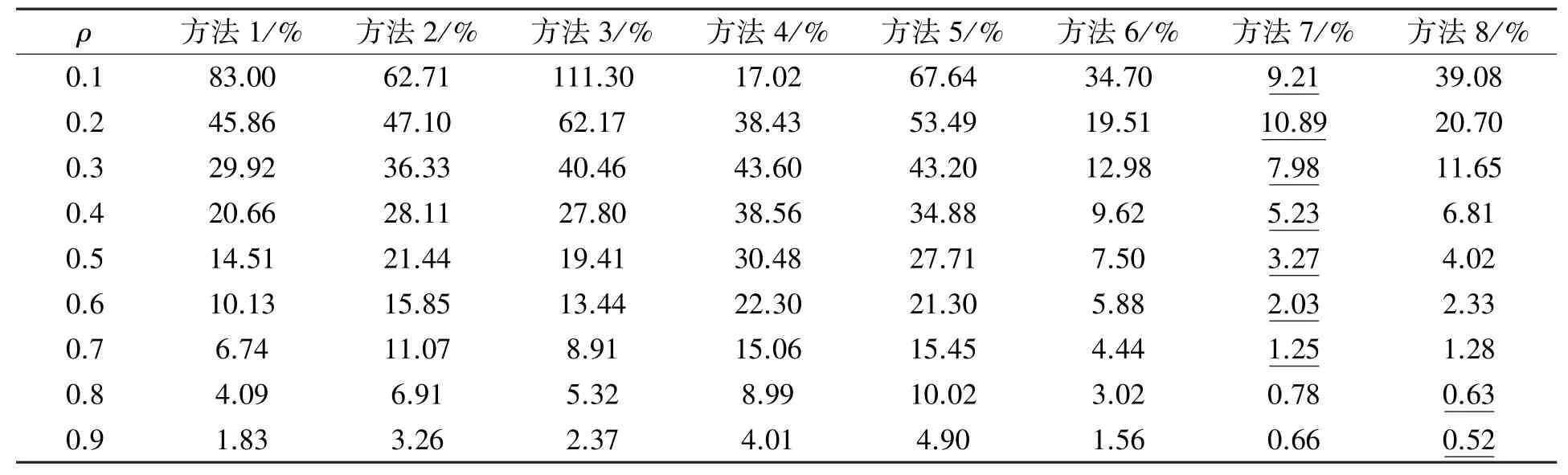
表5 ≥1，≥1时平均排队时间的平均相对百分比误差比较

ρ 方法1/% 方法2/% 方法3/% 方法4/% 方法5/% 方法6/% 方法7/% 方法8/%0.1 83.00 62.71 111.30 17.02 67.64 34.70 9.21 39.08 0.2 45.86 47.10 62.17 38.43 53.49 19.51 10.89 20.70 0.3 29.92 36.33 40.46 43.60 43.20 12.98 7.98 11.65 0.4 20.66 28.11 27.80 38.56 34.88 9.62 5.23 6.81 0.5 14.51 21.44 19.41 30.48 27.71 7.50 3.27 4.02 0.6 10.13 15.85 13.44 22.30 21.30 5.88 2.03 2.33 0.7 6.74 11.07 8.91 15.06 15.45 4.44 1.25 1.28 0.8 4.09 6.91 5.32 8.99 10.02 3.02 0.78 0.63 0.9 1.83 3.26 2.37 4.01 4.90 1.56 0.66 0.52

5 结束语

本文提出将GI/G/1排队系统通过近似方法构建为MAP/PH/1排队系统，即具有马尔可夫性的排队系统，通过分析MAP/PH/1排队系统，得到GI/G/1排队系统的近似数量指标。数值试验结果表明当到达过程的平方变异系数小于1或ρ→1，本文提出的方法近似效果较优。后续研究可以对到达过程的平方变异系数大于1的情况进行修正，以提高近似分析的精度，或者利用这一方法研究更复杂的排队系统，例如GI/G/m排队系统以及排队网络等。