一类长度为2m的负循环码的重量分布
黄 山
(安徽警官职业学院,安徽 合肥 230031)
0 引言
有限域上循环码是线性码的一个子类,具有高效的编译码算法,因此被广泛应用于消费电子、数据传输技术等领域.有限域上负循环码是循环码的发展与推广,它不仅具有丰富的代数结构,而且具有高效的编译码算法,因此被广泛应用于最优码、自对偶码以及量子码的构造等领域.Berlekamp[1]首次研究了有限域上的负循环码.Blackford[2]利用有限域上的负循环码构造了自对偶码.Danev等[3]利用有限域上的负循环码构造了一类最小距离为5的最优码.Kai等[4-5]将有限域上的负循环码应用于量子码的构造,得到了极大距离可分量子码.因此,研究有限域上的负循环码是十分具有价值的工作.
有限域上负循环码的代数结构已得到深入的研究.Bakshi等[6]确定了有限域上长度为2m的自对偶负循环码的代数结构.Dinh[7]确定了有限域上长度为2ps的负循环码的代数结构.Bakshi等[8]确定了有限域上长度为2pn的负循环自对偶码和负循环自正交码的代数结构.Sharma等[9]确定了有限域上长度为2mpn的负循环自对偶码和自正交码的代数结构.最近,Wu等[10]确定了有限域上负循环码的代数结构,并将其应用于线性互补对偶码的构造.
确定有限域上负循环码的最小距离通常是困难的.2008年,Dinh[11]确定了有限域Fpa上长度为ps的负循环码的最小距离.最近,Dinh等[12-14]先后确定了有限域Fpm上长度为3ps、4ps和5ps的负循环码的最小距离.目前,关于负循环码参数的研究工作相对较少,因此,确定负循环码的参数是一个有趣且具有挑战性的问题.本文通过分圆陪集理论,确定了有限域Fq长度为2m的负循环码的参数,其中q是一个奇素数幂.
1 预备知识
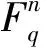
定义1设C是Fq上长度为n的线性码,如果对任意的(c0,c1,…,cn-1)∈C,恒有(-cn-1,c0,c1,…,cn-2)∈C,则称C为Fq上长度为n的负循环码.
下面介绍负循环码的代数结构.设R=Fq[x]/(xn+1)表示多项式环Fq[x]关于理想(xn-1)的商环.定义
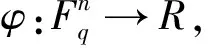
(c0,c1,…,cn-1)c0+c1x+…+cn-1xn-1,
且φ(C)={φ(c)|c∈C}.本文中,视C与φ(C)为同一概念.因此,有限域Fq上长度为n的线性码C是负循环码当且仅当C是商环R的理想.众所周知,商环R的每个理想都是主理想.设C=g(x)R=(g(x))是Fq上长度为n的负循环码,其中g(x)∈Fq[x]是一个首一多项式且整除xn+1.多项式g(x)称为负循环码C的生成多项式,h(x)=(xn+1)/g(x)称为负循环码C的校验多项式.在此基础上,给出不可约负循环码的定义.
定义2设C是Fq上长度为n校验多项式为h(x)的负循环码,当h(x)在Fq上不可约时,则称C为不可约负循环码.
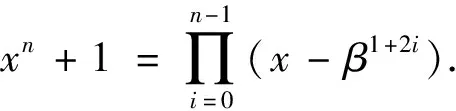
定义3设n与q互素,对任意i∈Z2n,q-模2n含i分圆陪集定义为
Ci={iqj(mod 2n)|0≤j≤li-1},
其中:li是使得iqli≡i(mod 2n)的最小正整数.
由定义3,容易验证,β1+2i在Fq上的极小多项式为
M1+2i(x)=∏j∈C1+2i(x-βj),
其中:C1+2i表示q-模2n含1+2i分圆陪集.设Δ={1+2i|0≤i≤n-1},由定义3,存在Z2n的子集Γ使得Δ=∪i∈ΓCi且Ci∩Cj=∅对任意i≠j.由此推出,xn+1在Fq上的不可约分解为xn+1=∏i∈ΓMi(x).进而,不可约负循环码具有如下的代数结构.
性质1设xn+1=∏i∈ΓMi(x),其中Γ和Mi(x)定义如上.设C是Fq上长度为n的负循环码,则存在i∈Γ,使得Mi(x)是码C的校验多项式.
2 长度为2m的不可约负循环码
下面研究Fq上长度为2m(m≥3)的不可约负循环码.为此,首先研究q-模2m+1含奇数的分圆陪集的性质.设q=1+2ab或q=-1+2ab,其中a≥2且b为奇数.设Δ={1+2i|0≤i≤2m-1},则有如下性质.
引理1(1)当q=1+2ab且m≤a-1时,则
(2)当q=-1+2ab且m≤a-1时,则
其中:0≤i≤2m-1-1.
(3)当q=±1+2ab且m≥a时,则q-模2m+1含所有奇数的分圆陪集,
证明(1)当q=1+2ab且m≤a-1时,2m+1整除q-1,所以C1+2i={1+2i}.显然,C1+2i(0≤i≤2m-1)各不相同,因此,

(3)对任意正整数e,利用数学归纳法可以证明,(±1+2ab)2e=1+2a+ebe,其中be为奇数.由此推出,
q2m-a=(±1+2ab)2m-a≡1+2m(mod 2m+1)
且
q2m-a+1=(±1+2ab)2m-a+1≡1(mod 2m+1).
因此,ord2m+1(q)=2m+1-a.于是,对每个1+2i,
C1+2i={(1+2i)ql|0≤l≤2m+1-a-1}.
下面证明C1+2i(0≤i≤2a-1-1)各不相同.假设存在0≤i,j≤2a-1-1且i≠j使得C1+2i=C1+2j,即存在l使得
1+2i≡(1+2j)ql(mod 2m+1).
(1)
由此推出,
1+2i≡(1+2j)ql≡
(1+2j)εl(mod 2a),
(2)
其中,
当εl=1时,由式(2)推出,i≡j(mod 2a-1),这与0≤i 2a≡(1+2j)(ql+1)(mod 2m+1). 因为m≥a,所以 2a≡(1+2j)(-1+2a)(mod 2a+1), 即2j(2a-1)≡1(mod 2a+1),矛盾.综上所述,结论成立. 设β是2m+1-次本原单位根,则β1+2i的极小多项式为 设NC(1+2i)是Fq上长度为2m校验多项式为M1+2i(x)的不可约负循环码. 定理1设q=1+2ab,其中a≥2且b为奇数. (1)如果m≤a-1,则NC(1+2i)的参数为[2m,1,2m]. (2)如果m≥a,则NC(1+2i)的参数为[2m,2m+1-a,2a-1]且重量为j的码字个数 Aj= 证明(1)当m≤a-1时,由引理1,M1+2i(x)=x-β1+2i.注意到 x2m+1=x2m-(β1+2i)2m= (2)当m≥a时,由引理1, 设γ=(β1+2i)2m+1-a,则ord(γ)=2a,所以γ∈Fq,即β1+2i是多项式x2m+1-a-γ的零点.因此,M1+2i(x)=x2m+1-a-γ.注意到 x2m+1=(x2m+1-a)2a-1-γ2a-1= 下面确定NC(1+2i)的重量分布.设c(x)∈NC(1+2i)是非零的码字,则存在f(x)∈Fq[x]且deg(f(x))≤2m+1-a-1,使得 c(x)= 由此推出,wt(c(x))=2a-1·wt(f(x)).因此,NC(1+2i)的每个非零码字的重量均被2a-1整除.特别地,wt(c(x))=2a-1l当且仅当wt(f(x))=l.因此, 定理2设q=-1+2ab,其中a≥2且b为奇数. (1)如果m≤a-1,则NC(1+2i)是参数为[2m,2,2m-1]的MDS码,且重量为j的码字个数为 (2)如果m≥a,则NC(1+2i)的参数为[2m,2m+1-a,2a-1]. 证明(1)当m≤a-1时,由引理1, M1+2i(x)=(x-β1+2i)(x-β1+2(2m-1-i))= x2-(β1+2i+β1+2(2m-1-i))x+1. 因为ord(β1+2i)=2m+1>8,所以β1+2i+β1+2(2m-1-i)≠0.容易验证,NC(1+2i)的对偶码NC(1+2i)⊥是Fq上由M1+2i(x)生成的参数为[2m,2m-2]的负循环码. A0=1,A2m-1=2m(q-1) 且 A2m=q2-1-2m(q-1). (2)当m≥a时,由引理1, 设λ=(β1+2i)2m-a,则ord(λ)=2a+1.注意到q2-1=2a+1(2a-1b-1)b,所以λ∈Fq2且λ+λq∈Fq.由此推出, (x2m-a-λ)(x2m-a-λq)= x2m+1-a-(λ+λq)x2m+1-a+λq+1∈Fq[x]. 因为β1+2i是(x2m-a-λ)(x2m-a-λq)的零点,所以M1+2i(x)整除(x2m-a-λ)(x2m-a-λq).比较多项式的次数可得,M1+2i(x)=x2m+1-a-(λ+λq)x2m-a+λq+1.又因为ord(λ)=2a+1,所以λq+1=(λ2a)b=-1且λ+λq≠0,即M1+2i(x)=x2m+1-a-(λ+λq)x2m-a-1. 设z=x2m-a且 x2m+1=z2a+1= [z2-(λ+λq)z-1]· [θ2a-2z2a-2+θ2a-3z2a-3+…+θ1z+θ0]. 比较等式两边的系数可得, 解得 i)当deg(f(x))≤2m-a-1时, 因此,wt(c(x))=(2a-1)·wt(f(x))≥2a-1. ii)当deg(f(x))≥2m-a时,设f(x)=f1(x)+x2m-af2(x),其中deg(f1(x))≤2m-a-1,deg(f2(x))≤2m-a-1,于是, θ2a-2f2(x)x2m-2m-a. 由此推出, wt(c(x))=wt(f1(x))+wt(f2(x))+ 特别地,当f1(x)=0时, wt(c(x))=(2a-1)·wt(f2(x))≥2a-1. 当f1(x)≠0且f2(x)≠0时,注意到λq=λ-1+2ab=-λ-1,所以 由此推出, (-1)jλ2j+1(λ2+1)[λ2(i-j)-(-1)i-j]=0 ⟺λ2(i-j)-(-1)i-j=0. 当i-j为奇数时,λ2(i-j)=-1,这与ord(λi-j)=2a+1≥8矛盾.当i-j为偶数时,λ2(i-j)=1,即2a|(i-j).又因为1≤i,j≤2a-2,所以i=j.即 由此推出wt(c(x))≥1+1+2a-3=2a-1.综上所述,NC(1+2i)的最小距离为2a-1. 例1设n=24,在F9上,xn+1=(x4+ω)(x4+ω3)(x4+ω5)(x4+ω7),其中ω是F9的本原元. 由定理1,F9上有4个不同的不可约负循环码且它们的参数均为[16,4,4].它们的重量分布为1+32z4+384z8+2048z12+4096z16. 例2设n=24,在F3上,xn+1=(x8+x4+2)(x8+2x4+2). 由定理2,F3上有2个不同的不可约负循环码且它们的参数均为[16,8,3].经Magma验算,它们的重量分布为1+32z3+384z6+2048z9+4096z12. 本文通过计算q-模2m+1分圆陪集,确定了Fq上长度为2m的不可约负循环码的生成多项式.利用生成多项式的结构,确定了Fq长度为2m的不可约负循环码的最小距离,并给出了一类不可约负循环码的重量分布.
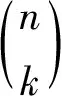
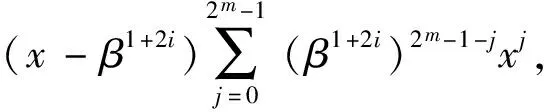

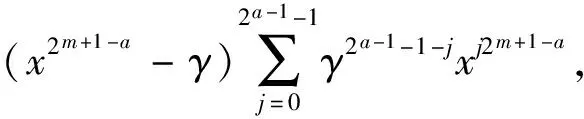


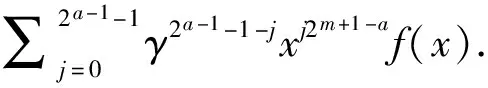
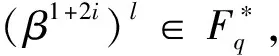
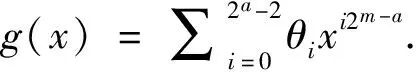


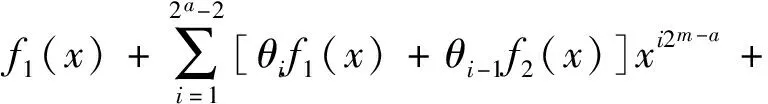
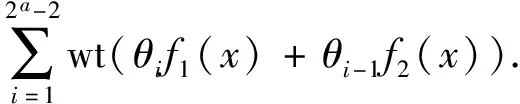

3 结语

