基于商空间粒度的序关系及其转换研究
李海霞
(莆田学院 新工科产业学院,福建 莆田 351100)
0 引言
日常生活中人们时刻进行着观察、对比、决策.要进行对比,首先要对事物按某种尺度进行量化,在量化的基础上排泛序[1]、求解问题.对于比较复杂的问题,在更小的细节上划分的序(微观序)下解决,会陷入细节,难以求解,或者说求解的复杂度比较高,这时,需要进行转换,将微观序转化为更粗粒度上的序(宏观序),在该序上解决问题,可以降低求解问题的复杂度,提高求解效率.
文章基于商空间粒度理论,讨论了元素上的序(微观序)到集合上的序(宏观序)的转换、集合上的序(微观序)到集合幂集上的序(宏观序)的转换以及信息表上序的转换,给出了微观序到宏观序转换的步骤,并举例说明微观序到宏观序的转换在人们生活中的应用.
1 相关概念
1.1 商空间粒度理论
粒度(Granularity)[2-6]就是取不同大小的对象,是描述模糊和不确定性对象的工具.也就是说,将原来“粗粒度”的大对象分割成若干个“细粒度”的小对象,或者把原来若干个“细粒度”的小对象合并成一个粗粒度的大对象,进行研究.我国学者张钹院士曾经指出:“人类智能的一个公认的特点:人们能从极不相同的粒度空间上观察和分析同一问题.人们不仅能在不同粒度世界上进行问题的求解,而且能够很快地从一个粒度世界跳转到另一个粒度世界,往返自如,毫无困难.这种处理不同粒度世界的能力,正是人类问题求解的强有力的表现”[7].
在求解实际问题的过程中,根据求解问题的不同,需要不同粒度世界的描述.有时候解决同一问题时,同时需要若干不同粒度的世界.商空间理论[6-7]用三元组(X,f,T)描述一个问题,其中X表示问题的论域;f是论域的属性,是对对象X的特征的刻划;T是论域的结构,指论域X中各元素的相互关系(如距离、半序、拓扑等).分析或求解问题(X,f,T),是指对论域X及其有关的结构、属性进行分析、研究.比如,当X很复杂时,可以对X的大小粒度进行简化,产生一个新的较大粒度的论域[X],那 么 把 原 问题(X,f,T)变成新的层次上的问题([X],[f],[T]).即从较粗粒度[X]去考察问题.
1.2 商空间族的性质
商空间族[7]即所有可能的商空间构成的集合.
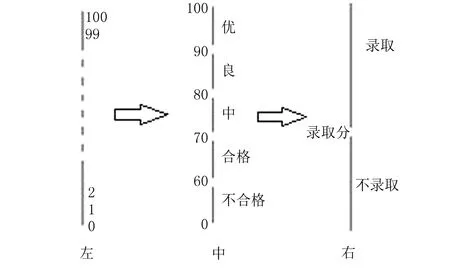
定义1给定一论域X,设R是X上一切等价关系的全体.定义R1,R2∈R,若x,y∈X,xR1y⇒xR2y,则称R1比R2细,记为R2 定义2给定X上的两个拓扑T1,T2,设Ti的全体开集构成的集合族Oi,i=1,2.若O2是O1的子族,则称T1比T2细,记为T2 定义3设(X1,T1),(X2,T2)∈(X,T),若X1 定理1在(X,T)上定义如上的“<”关系,则(X,T)构成一个完备半序格. 从不同粒度来考察问题,所有可能选取的商空间和结构就是(X,T)中的元素,文章主要讨论对于给定的问题,如何从(X,T)中选取更“粗”的元素进行求解——将论域中的子集当作新的元素进行研究,用数学术语来讲,就是对X进行划分,得到商集[X],然后对[X]进行研究. 没有什么东西是绝对微观的或绝对宏观的.采用微观的观点还是宏观的观点主要取决于观察者的目的、理解和所处的环境等.不同的观察者对相同的事物有不同的尺度[8],因此对于相同的事件,不同的观察者会存在不同的观点和不同的解决方法,即所谓的“横看成岭侧成峰”. 泛系相对性[9-11]是指系统的相对性和关系的相对性,是形成宏观序和微观序的基础,宏观和微观不是绝对的,是相对的.根据泛系相对性,宏观序是一般的序,而微观序是从更小的细节上划分的序.从粒度的观点来看,宏观序是在比微观序更粗的粒度空间研究序. 由于解决问题或决策的需要,经常需要将微观序转换成宏观序[12-13],在更粗的粒度空间解决问题,以提高求解问题的效率,降低求解问题的复杂度. 如何将微观序转换成宏观序呢? 结合1.2中商空间族的性质,接下来讨论对于给定的问题(微观序下),如何通过商化,从(X,T)中选取合适的元素并定义宏观序,以达到简化问题的目的. 定义4集合A和B上定义序关系≤ ’: 满足集合B中的元素或者大于集合A中的元素,或者与集合A中的元素没有关系.将A、B上的这一关系记为g,则g= { 例1:设集合A= {a,b, 0, 1 },集合A上的序关系ƒ = 图1 集合A上的序关系f 众所周知A= A的滤子:F= { 1,a}. A的理想:I= {b,0 }. 根据定义4,在F和I之间存在序关系≤′,将集合上的这一序关系记为g,则 g= { {F,I} ,≤′} = { < {0,b},{1,a} > }.如图2所示. 图2 { F,I }上的序关系g 序关系ƒ 到序关系g的转化如图3所示. 图3 序关系ƒ到序关系g的转换 显然,序关系ƒ= 从粒度的角度来看[4-5],微观序ƒ和宏观序g是不同的粒度层次,宏观序g是更粗的粒度空间上的序.在更粗粒度空间上解决问题,能降低求解能提的复杂度. 定义5设A是一个集合,A的子集B⊆P(A)(P(A)是集合A的幂集合),B= {B1,B2,B3, …},对于任何X∈Bi如果存在集合Y, 并且满足Y∈Bj,X⊆Y,则Bi⊆Bj. 例2:设集合A= {{a,b,c,d},{a,c},{a,b}, {a}},集合A上的序关系ƒ′= 图4 集合A上的序关系ƒ′ 构造满足定义5的集合B,B={{{a,b,c,d}},{{a,c},{a,b}},{{a}}},则B上有包含关系⊆′,集合B和B上的包含关系⊆′形成序关系g′= 图5 集合B上的序关系g′ 序关系ƒ′到序关系g′的转换如图6所示. 图6 集合上的序到集合的幂集上的序的转换 容易得知,序关系ƒ′= 同样地,从粒度的角度[4-5]来看,微观序ƒ′和宏观序g′是不同的粒度层次,宏观序g′是更粗粒度空间上的序.在更粗粒度空间上解决问题,能降低求解能提的复杂度. 信息表是粗糙集理论中对知识进行表达和处理的基本工具.信息表与泛权场一一对应,故可以将信息表的研究转变为对泛权场的研究. 经典粗糙集理论中,论域U是元素的集合,未能显化事物和事物的区别,所以对事物的认识不是很清晰.为此,引入了元素语义,构成泛权场,泛权场显化了事物之间的区别,使得对事物的描述更全面,对事物的认识更清晰. 定义6泛权场[1]:在一个广义系统S=(A,B)中,如果满足B:A→W,则S就是一个泛权场,其中W为A的泛权集. 定义7子泛权场:设泛权场fU:U→W,fX:X→W,集合X⊆U,如果对∀x∈X,不存在y∈U-X,使得fX(x)=fU(y),称fX是fU的子泛权场. 特别地,设∅ 也是fU的子泛权场. 定义8偏序“⊆”(“⊇”)上的宏观序“⊆*”(“⊇*”):设fX、fY∈P(B),∀fx∈fX和∀fy∈fY要么fx⊆fy(fx⊇fy)或fx,fy没有“⊆”关系,则有fX⊆*fY(fX⊇*fY).其中B为某泛权场所有子泛权场的集合;P(B)为B的幂集. 例3:假设有如图7所示的泛权场布尔代数: 图7 某泛权场布尔代数 根据定义8,对图7某泛权场布尔代数进行商化,如图8所示. 图8 某泛权场布尔代数的商化 商化后得到如图9所示的商化后的序. 图9 商化后的序 在此基础上,根据定义8,对图9中的序继续商化,如图10所示. 图10 对商化后的序的商化 构造出更粗粒度空间上的宏观序(线型序),如图11所示. 图11 商化后的宏观序(线型序) 在这里,将原来的泛权场布尔代数通过求商、再求商,最终变成了线形序.大大降低了问题的复杂性. 定理2任何一个泛权场布尔代数,通过商化,最终可转变为线形序. 定理3商化之后的偏序或线形序中,最小元为原布尔代数的理想,最大元为原布尔代数的滤子.商化越厉害,对应的理想和滤子也越大. 为了提高问题的求解效率,降低求解问题的复杂度或者决策的需要,经常需要结合商空间粒度理论将微观序转换为宏观序,在更粗的粒度空间分析、解决问题.具体转换步骤如下: Step 1 分析研究当前微观序的元素和元素上的序关系(微观序); Step 2 根据1.2商空间族的性质,在微观序的基础上构造更粗的粒度空间——将论域中的子集当作新的元素进行研究; Step 3 定义出粗粒度空间上的序关系(宏观序). Step 4 如有需要,再重复step1、step2、step3步,构造出更粗粒度空间上的序. 微观序从更细节的地方观察和控制事物,而宏观序从整体上、全局上观察和控制事物.下面举一个日常生活中微观序到宏观序转换的简单例子. 例:升学考试过程:学生考试,获得分数;学校根据招生人数、学生分数高低以及排名,决定是否录取. 考试是量化学生学习好坏的一个工具,考得的分数是量化的结果.通常情况下,按照学生分数的高低排名(图12左),这是学生及家长所关注的;对老师来说,更关注学生在各个分数段的分布情况(图12中);而对升学来说,只关注哪些学生被录取(图12右). 图12左边的序关系是微观序,不适合做决策.对于学校来说,他们只需要确定一个升学的录取分,如果考生的成绩高于录取分,则录取,否则,不予录取. 图12 微观序到宏观序的转换 可以看出,对于决策者学校来说,从宏观序进行升学录取的效率更高. 人们在微观序下,分析问题、解决问题的效率不高,经常需要从微观序转换到宏观序,从宏观上做决策. 文章结合商空间粒度理论,重点讨论了元素上的序到集合上的序的转换、集合上的序到集合幂集上的序的转换以及信息表上序的转换,给出了微观序到宏观序转换的步骤,并举例说明微观序到宏观序的转换在人们生活中的应用. 通过将微观序转换为宏观序,对复杂问题进行更粗的粒度划分, 将其转化成较为简单的问题, 从而有助于对复杂问题的分析与求解.1.3 微观序和宏观序
2 微观序到宏观序的转换
2.1 元素上的序到集合上的序的转换
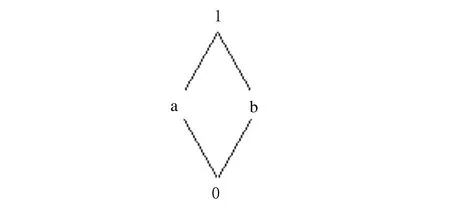

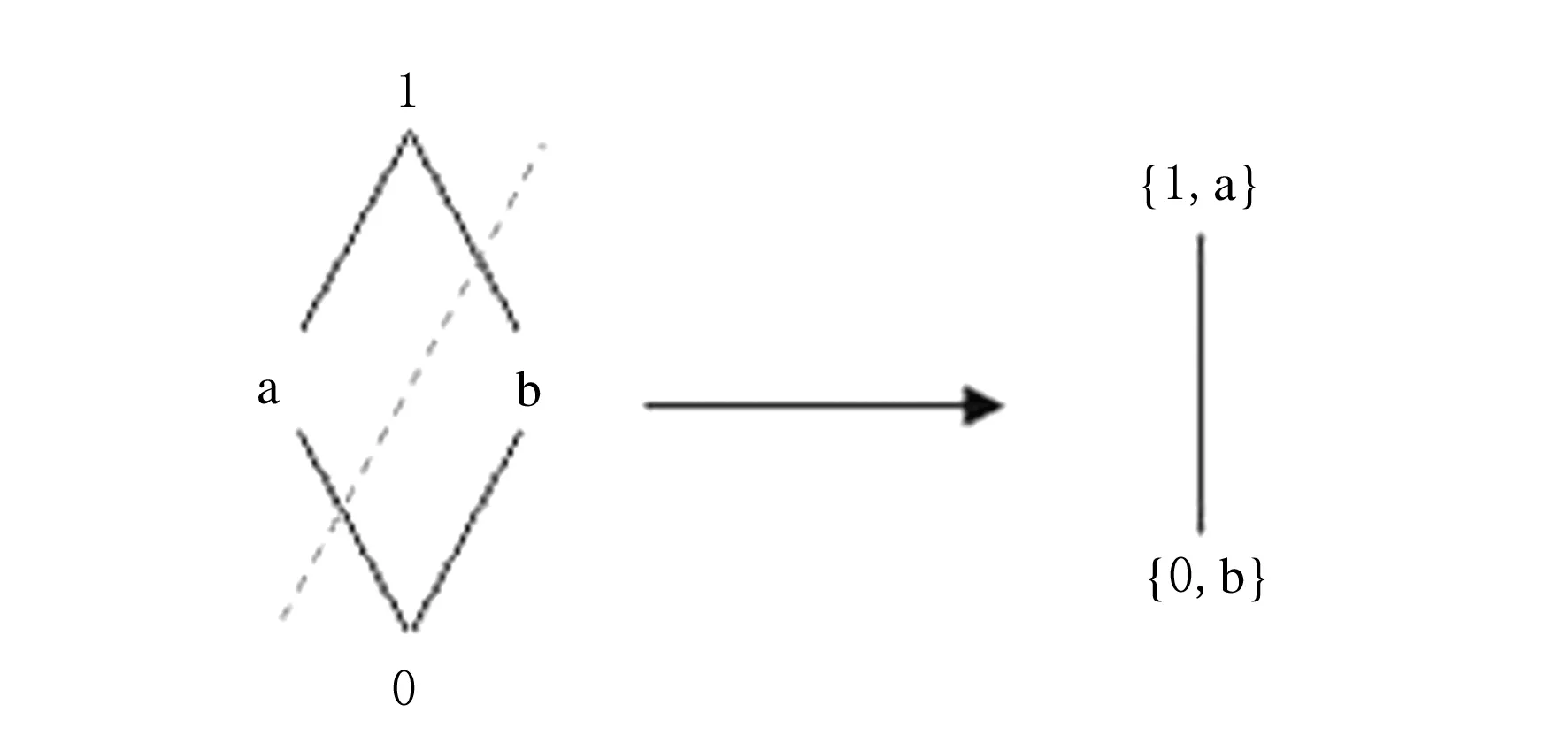
2.2 集合上的序到集合幂集上的序的转换
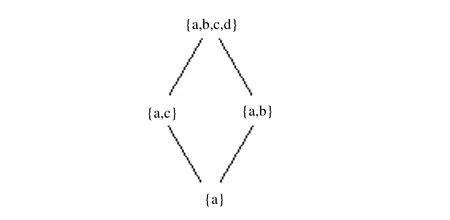
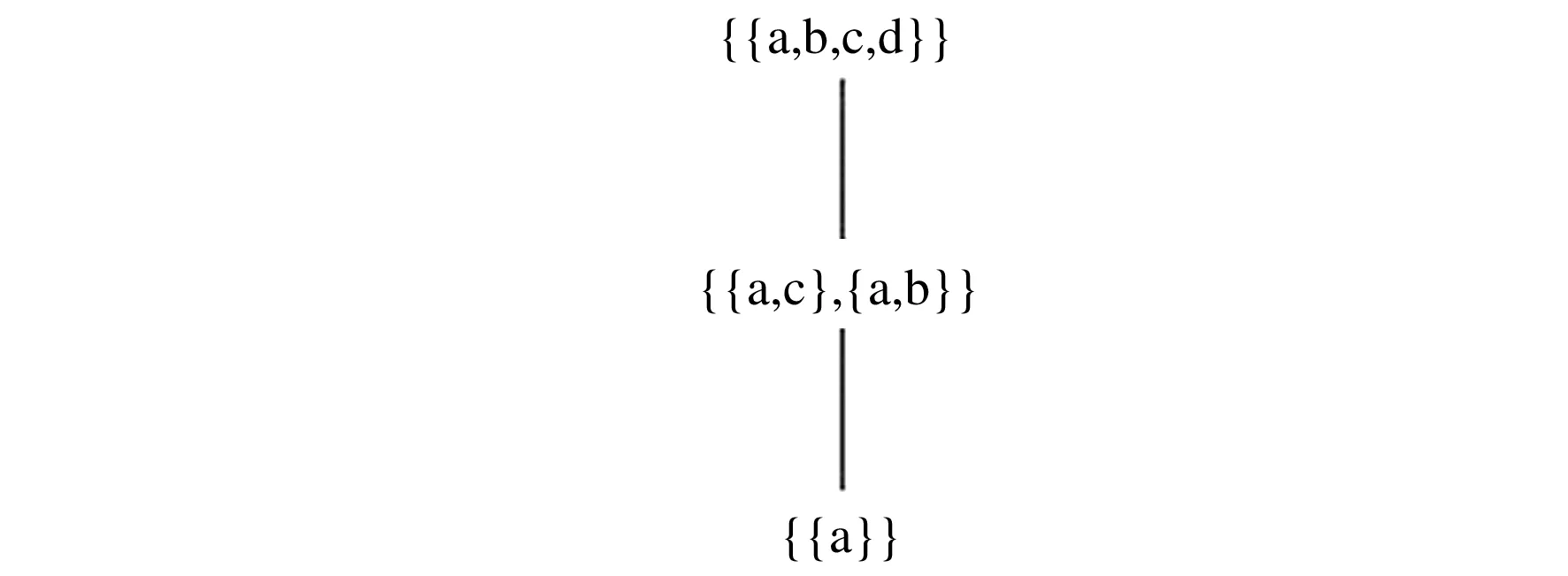
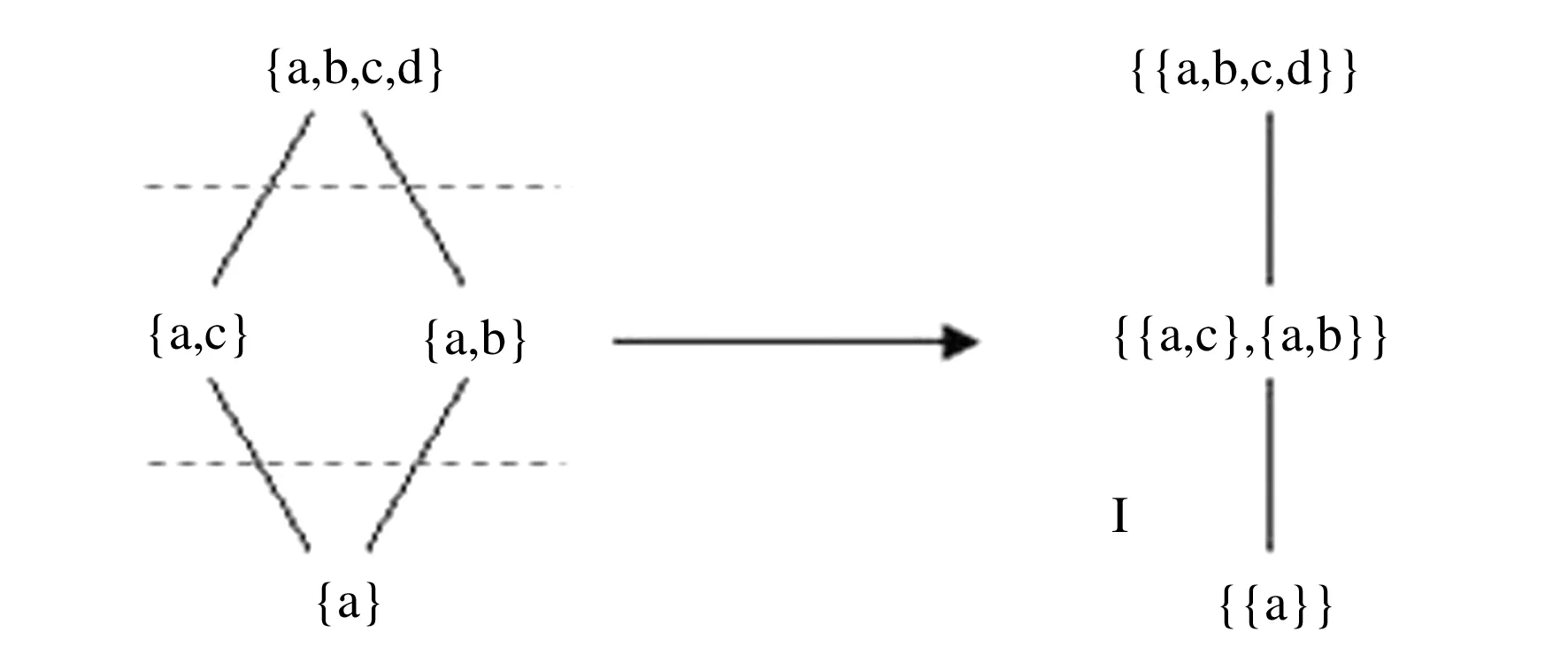
2.3 信息表上序的转换


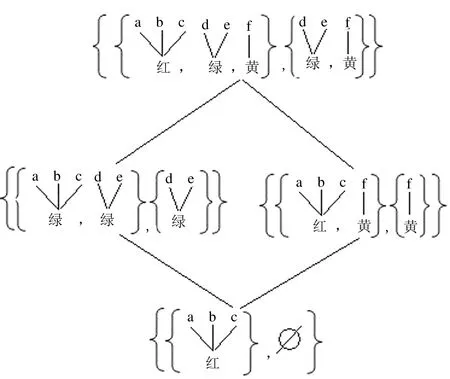
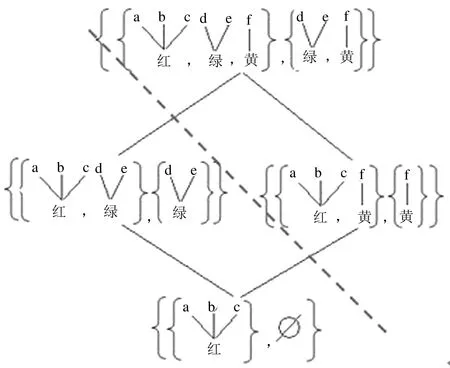
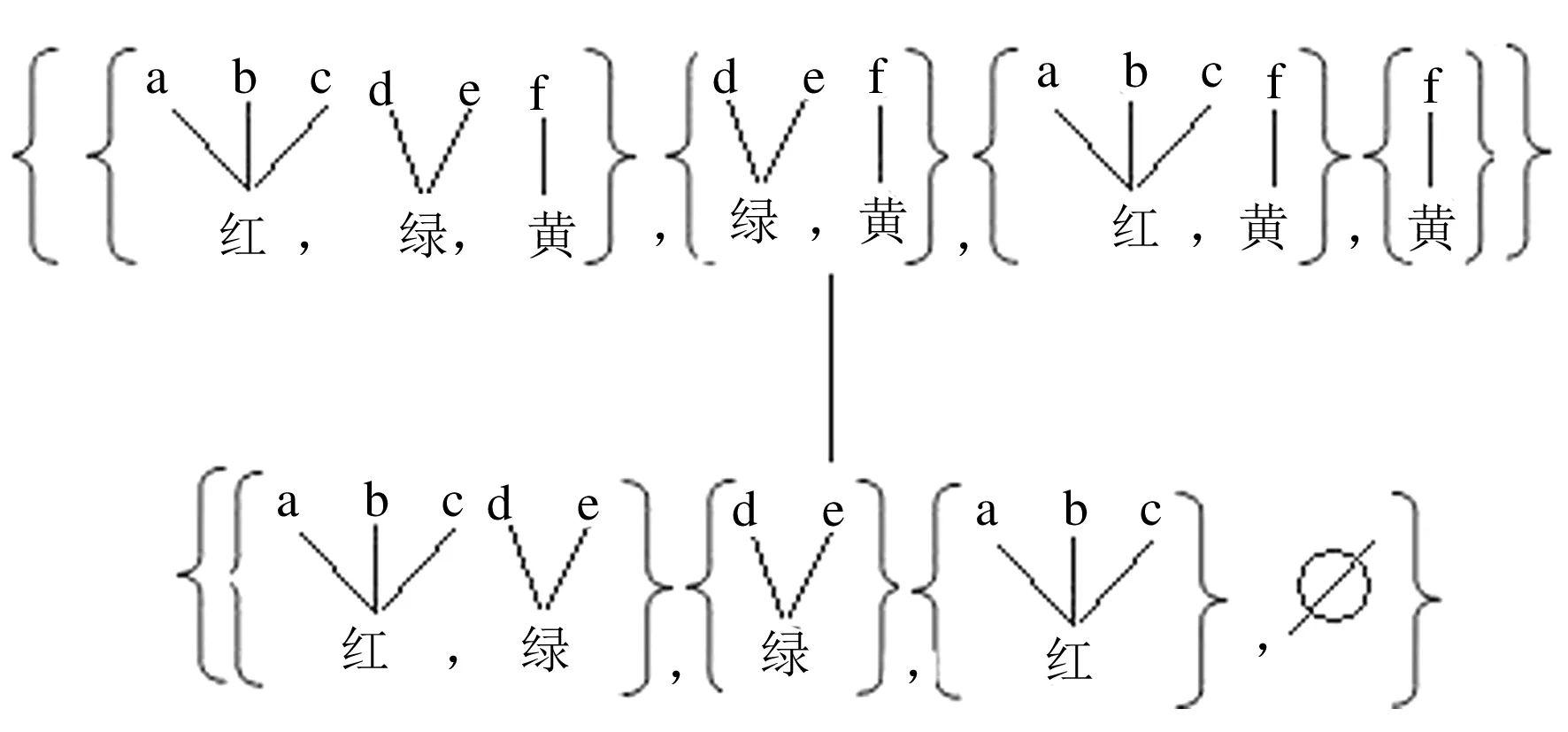
2.4 从微观序到宏观序转换的方法
2.5 从微观序到宏观序转换的应用
3 结语

