三维引擎动画关键技术优化设计研究

丁 磊

(安徽文达信息工程学院 计算机工程学院，安徽 合肥 231201)

随着三维引擎动画诸多关键技术的发展与成熟，使用三维引擎动画作为展示和交互方式的现象日趋普遍，人们对三维动画的细节美感要求也越来越高，导致其数据量和模型复杂程度也水涨船高，对应存储与网络传输所需消耗的计算机资源也逐渐增加[1].因此把重构模型失真程度控制在满足使用要求的前提下，大幅提高三维动画的压缩比是一个有待解决的技术问题.针对这个问题，前人提出了多种解决方案，

罗国亮等[2]为了提高三维动画数据的压缩比与压缩时效性，提出了一种基于三维模型顶点序列调整的优化压缩算法，采用不同类型动画数据对其进行测试，结果表明，该算法在压缩比和压缩速度上比传统算法有所提升.王美丽等[3]针对三维模型浮雕在解压模型过程中容易出现细节信息丢失的问题，提出了适用于三维复杂网络模型生成数字浮雕的优化方案，实验结果表明，该方案能有效降低构建三维数字浮雕模型重构过程中的信息损失.于兵科[4]针对传统三维动画模型在解压重构后动画效果有所劣化的问题，采用动力学方法，以物理引擎为基础，设计出一套改进的三维模型重构算法，实验结果显示，该算法重构出的三维模型动画效果更接近未解压前的状态，动画信息损失更少.综上所述，行业内专家对模型压缩优化方法做了详细研究，但是较少涉及流式传输，因此本文设计一种三维引擎动画的优化压缩算法，其对于降低计算机处理负担、提高三维动画的网络传输速度、实现动画数据的流式传输具有一定价值.

1 面向三维引擎动画的改进压缩算法

1.1 基于整数规划的时域聚类算法

三维引擎动画的压缩技术呈现出由单分辨率压缩向多分辨率压缩转变的趋势，因为多分辨率压缩又称为渐进式压缩，支持对几何模型的渐进传输，其网络利用效率更高[5-8].本研究提出一种渐进式压缩的优化改进算法，其算法的压缩流程如图1所示.

图1 改进的三维引擎动画压缩算法流程

如图1所示，算法的压缩核心步骤为：①读取三维引擎动画文件，读取各关键帧里的顶点坐标数据与拓扑数据;②通过计算待求指标的顶点在所有帧中坐标连成的空间曲线，然后用每帧的指标加权值得到每个顶点的曲率与绕度；③采用提出的时域聚类算法将要素相似的帧聚为一类;④对时域聚类结果的每一类关键帧进行空域分割，使顶点运动趋势相似且拓扑连续的点聚为一类;⑤完成对时空两者的聚类后，再对输出数据进行图傅里叶变换以进一步提高压缩效果;⑥对经过图傅里叶变换的系数值进行SPECK编码，然后结合前面的连接数据与编码后的数据输出压缩后的三维动画文件.若要对模型解压重构，按照压缩流程逆向执行即可.

为了处理相邻帧的冗余信息，提出一种基于整数规划的时域聚类算法，通过它对动画帧进行聚类，让相似度高的网络帧聚集为一类，以便下一步消除这些冗余数据.考虑到时域聚类结果中每类所含帧数都为整数，因此普通的时域聚类并不适合此次研究[9-12].采用每帧顶点的曲率和绕度来代表其运动剧烈程度，这里的曲率、绕度是指由所有帧中待求曲率顶点组成的曲线，与每帧交点的曲率与绕度，其数值通过差分法求得，以减小拟合误差，从而得到每帧的运动图，以纵坐标为顶点模型运动值，横坐标为顶点索引，则可以用相邻帧的运动图与坐标轴所围面积的差异大小来衡量运动剧烈程度.因此，该规划问题的目标函数就可以定义为每类偏离平均面积的平方和，约束条件为所有类含帧数之和等于总帧数，这样，普通时域聚类问题被转化成为非线性约束的整数规划问题.具体的，第i个顶点在每帧中的曲率以及绕度的具体求解公式如下：

(1)

(2)

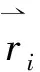
MO=αk+(1-α)τ，

(3)

其中:k、τ代表曲率、绕度，α代表权重，一般情况下两者重要性相同，α取0.5，特殊情况下应适当调整.如果模型几乎是在单个平面上移动，则曲率指标重要性更高，α需要调大一些.

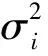
(4)

其中:t为i类所含帧数，为了控制算法运行过程中所消耗的存储空间，定义一个权重系数β，表示误差在目标函数中所占比重.另外，设空域分割一帧保存结果需要的存储空间为t，则目标函数定义为：

min{βL(t1,…,tk)+(1-β)Kt}=

(5)

其中:K为聚类后的类别数量.最后帧数的约束条件如下：

(6)

其中:Nkey为关键帧的数量.至此，时域聚类问题便完整转化为非线性约束下的整数规划问题，然后采用蒙特卡罗方法求解.

1.2 基于动画对象运动特性的分割算法

对数据进行时域聚类后，还需要对聚类结果中每一类的关键帧进行空域分割，其目的是为了把模型中相似的各顶点划分为同一块[13-15].如果两顶点的欧式距离与其时域聚类的簇内运动期望之差的加权均值很小，算法就认为两顶点相似度高，应聚为同一类，其中关键帧通过逐帧计算该类当前帧与其他各帧的帧距总和，然后取该值最小的对应帧为关键帧.设时域聚类第k类的关键帧f被空间分割为S块，应选择合适的S值使分割结果中每块内含有顶点之间的运动量差别最小，其值由后续实验确定，则目标函数可表示为：

(7)

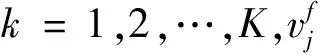
(8)

下面以第t类的关键帧f为例阐述空域分割的过程，其计算流程如图2所示.

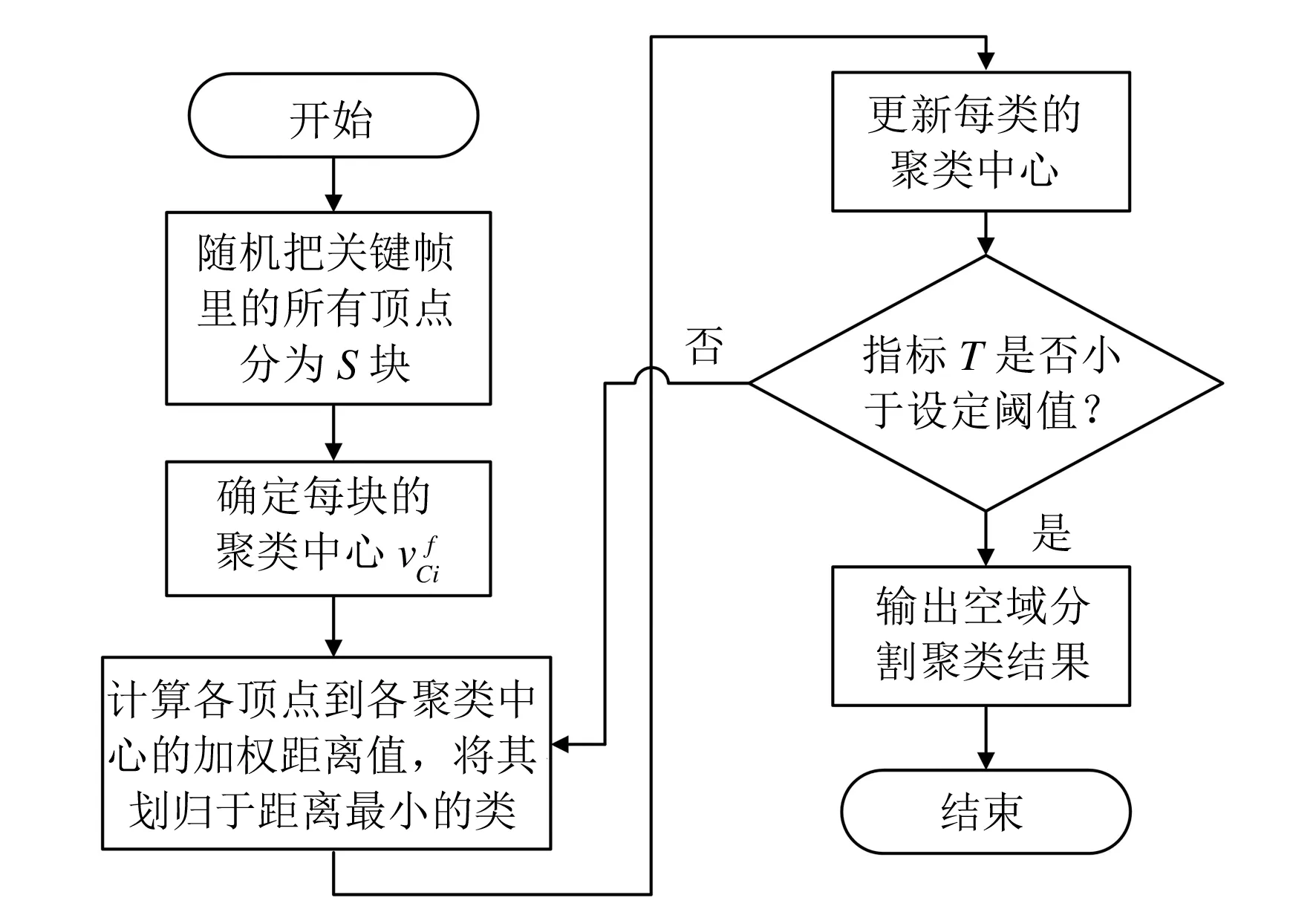
图2 空域分割聚类流程图

(9)

完成时域、空域聚类后，再对所有处理后的数据进行图傅里叶变换，进一步提高压缩效果.设变换对象为第i类的第j块Sij.先运用聚类后的动画数据拓扑求出Sij的拉普拉斯矩阵L，计算公式为L=D-A.D是对角矩阵，对角上的元素为对应顶点的度，A为邻接矩阵，由数据的拓扑信息求得，两顶点有边对应位置记1，无边记为0.另外，L、D、A均为‖Sij‖×‖Sij‖的矩阵，‖Sij‖代表第i类里第j块的顶点数量.求出拉普拉斯矩阵L后，再求出对应的特征向量V，同为‖Sij‖×‖Sij‖的矩阵.最后，把每帧里相应顶点的三维坐标分别取出，投影到对应部分的基上，计算得到相应系数，再根据输出文件的质量、网络传输速度、模型所属行业等要求，从中选出kn个基较为重要的系数，以备下一步编码.

为了满足当下主流的渐进传输要求，对经过图傅里叶变换后提取的系数采用嵌入式编码算法编码，而常见嵌入式算法中SPECK编码在独立编码、编码速度方面具有明显优势，因此研究选择SPECK算法对图傅里叶变换输出系数进行编码.

2 改进压缩算法的压缩效果分析

2.1 改进压缩算法的压缩对比实验参数设置

针对设计好的算法，选用两种常见的三维引擎动画模型Human、Cat，它们的模型拓扑信息、几何信息如表1所列.实验使用的三维模型通过3 ds Max2017软件构建，实验在惠普251-050cn型台式计算机平台进行.对其使用该算法与常见的三维动画压缩算法Luo et al.2013、Vasa et al.2010进行对比压缩实验，以验证该算法的压缩效果，后两种算法与本算法有相似之处，但它们仅对三维模型的几何信息进行压缩，不压缩拓扑信息，且不考虑时域冗余.

如表1所列，模型的几何信息远大于拓扑信息.在确定算法的关键参数时，对于空域分割中的距离权重系数χ，考虑到算法需要较高的空间连续性以尽可能减少分割后每块所含不连续顶点的数量，从而保证下一步图傅里叶变换的准确性，该权重系数设置范围为0.5～1，用以保证聚类后数据的空间连续性，具体取值通过Human、Cat模型的分割后χ权重系数与不连续点关系实验确定，其实验结果如图3所示.

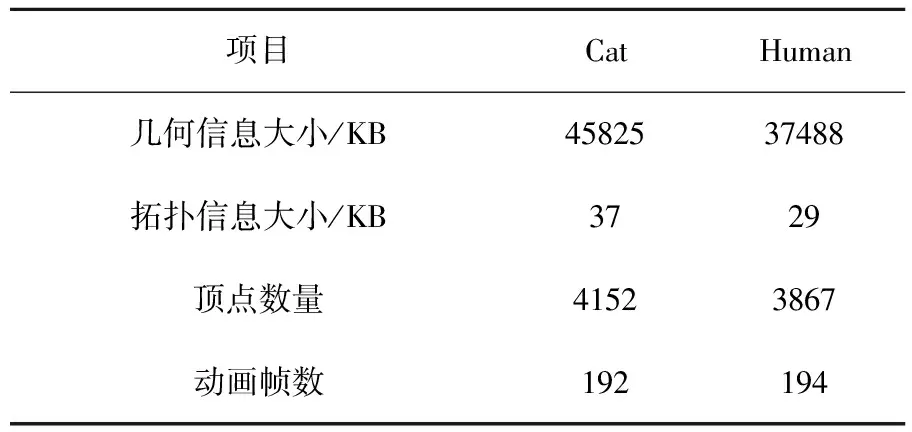
表1 用于测试的三维引擎动画模型部分参数

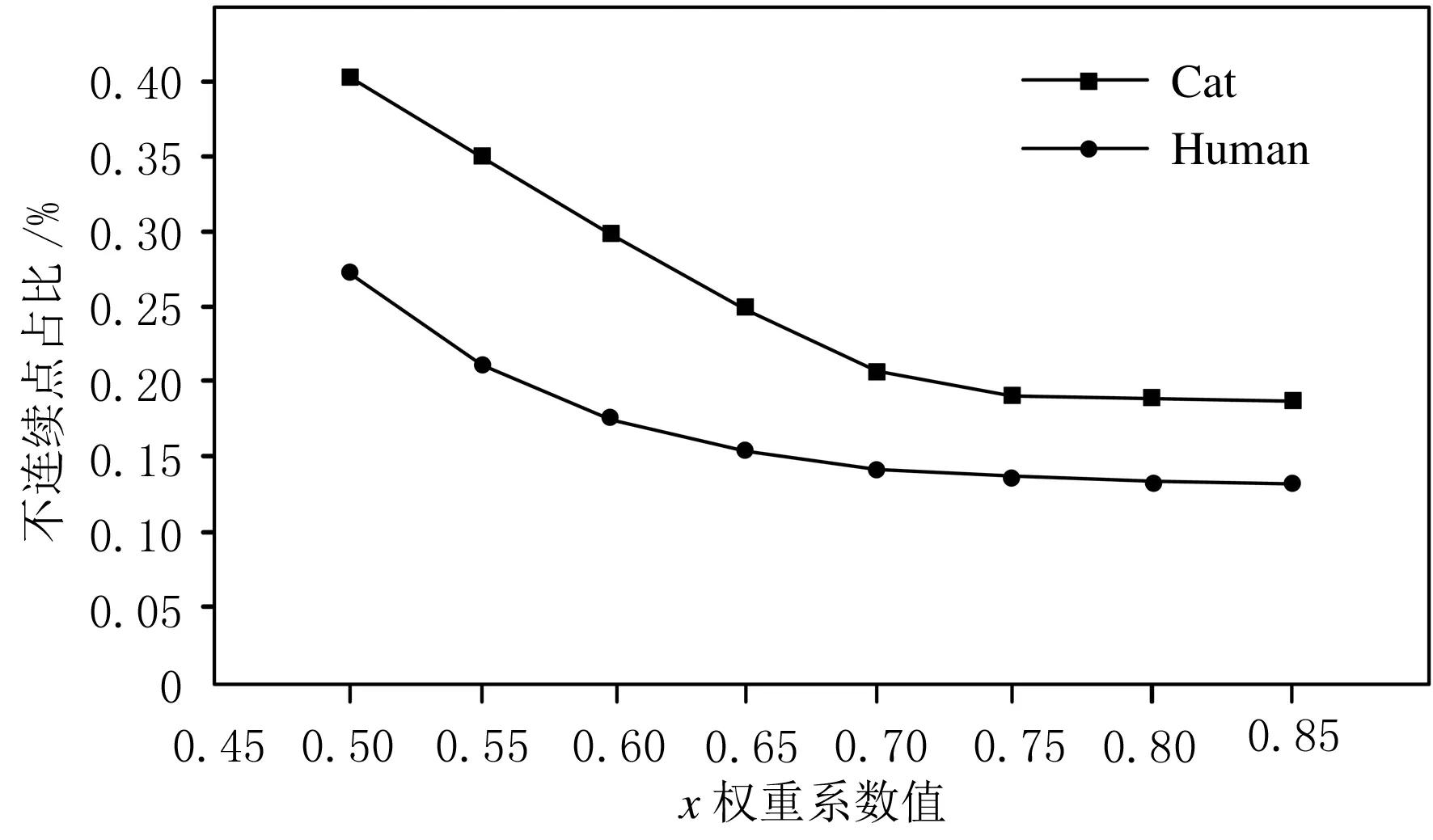
图3 分割后χ权重系数与不连续点占比的关系

分析图3可知，当χ权重系数小于0.8时，随着系数的增大，两模型中不连续点占比下降明显，但下降速度有所减缓；而当权重系数接近0.8以后，随着系数的增大，不连续点占比变化已不明显，即这时增加系数对减少不连续点的作用已极其有限，所以χ权重系数选择0.8较为合理.按照同样的思路，可以确定kn取值较为合理.

2.2 三维引擎动画模型压缩对比试验结果分析

选好算法系数后，采用常规的压缩率-重构误差率曲线来对比各算法效果，压缩率由压缩后的总数据大小除以模型顶点个数与动画总帧数的乘积.各算法对Human三维引擎动画压缩效果如图4所示.

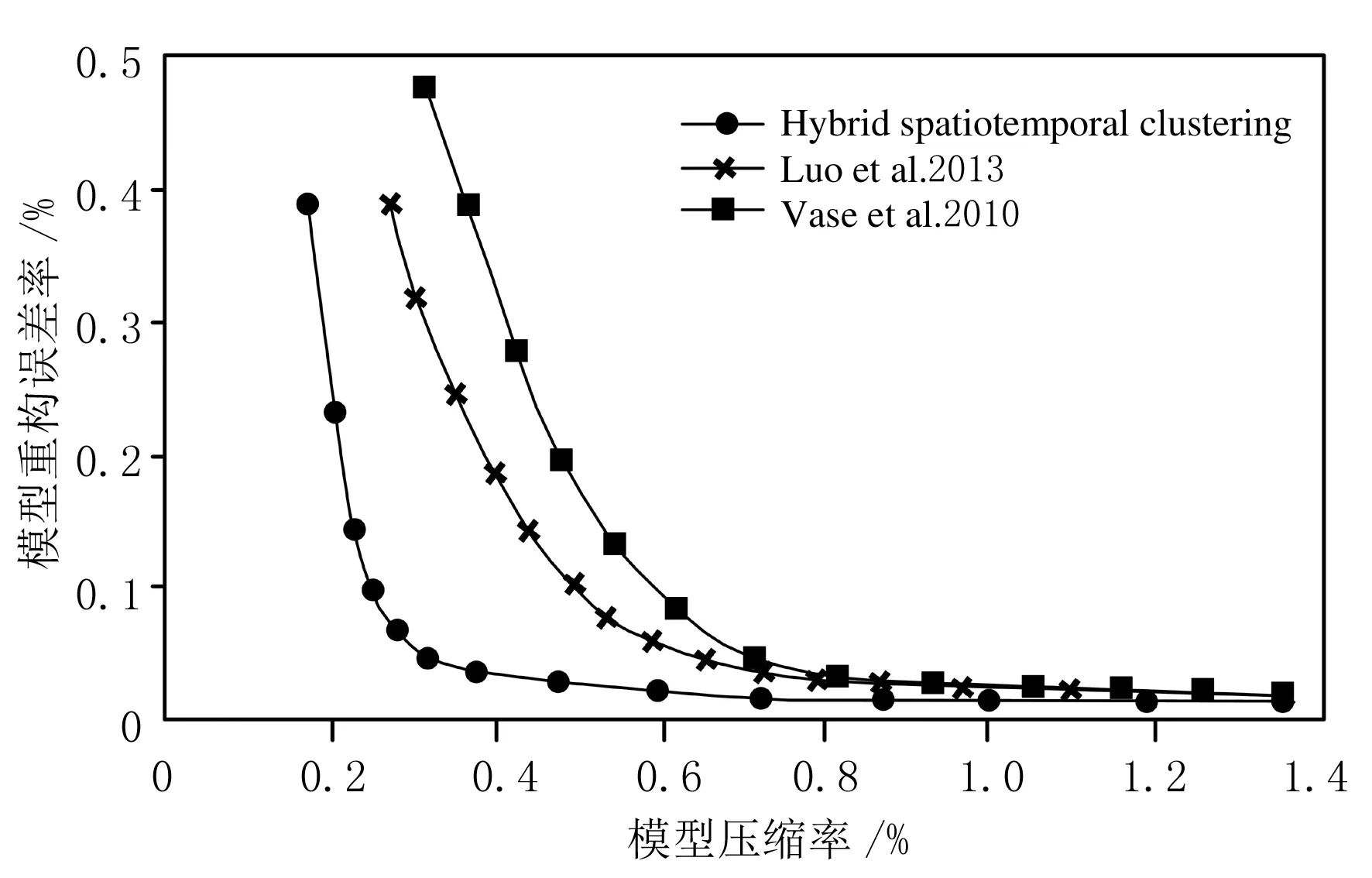
图4 各算法对Human三维引擎动画模型压缩效果

图4中的“Hybrid spatiotemporal clustering”即为本研究提出的混合时空聚类压缩算法.分析图4可知，在3种算法都存在数据的范围内，达到同一模型压缩率时，此算法的模型重构误差率最小，即模型重构时失真程度最小，而在达到同一模型重构误差率时，该算法的压缩率又远远小于其他两种算法，并且此算法在压缩率大于0.3%时，减小压缩率(即提高压缩程度)带来的模型重构误差增长微小.综上所述，该研究提出的新型压缩算法对Human动画模型的压缩效果、重构效果明显优于传统压缩算法.为进一步确认算法效果，再对Cat三维动画模型进行压缩比对测试，结果如图5所示.

图5 各算法对Cat三维引擎动画模型压缩效果

如图5所示，对Cat三维引擎模型的压缩、重构效果与对Human的大体一致，仅少数细节有所不同.因为Cat动画模型较之Human更为复杂、运动变化更为激烈，所以在各算法下整体重构误差率均较高，且在同样重构误差率下，压缩效果整体都更差.算法间对比结果同样显示出，该研究提出的压缩算法在压缩效率、重构误差方面具有显著优势.

3 结论

本文针对三维引擎动画的关键技术之一的压缩技术进行了优，在分析了前人解决方案的基础上，提出了一种基于时域、空域双重聚类的三维动画压缩算法.该算法创新性地把目标函数、曲率、绕度进行了重新定义，从而把基于整数规划的时域聚类问题转换成为非线性约束的整数规划问题.使用该算法与其他三维动画压缩算法进行压缩与重构实验，在相同模型压缩率条件下，使用该算法进行模型重构时，重构误差率最小，而在同一模型重构误差率时，该算法的压缩率又远远小于其他算法，在小压缩率、中等压缩率、大压缩率条件下，该算法的重构误差率较对比算法分别降低了至少45%、20%和3%.结果说明该研究提出的新型压缩算法对三维引擎动画的压缩率、重构误差有一定的优化效果.