基于小波阈值的电能质量扰动信号去噪研究
王昌盛,丁 松,郑 平
(安徽理工大学 电气与信息工程学院,安徽 淮南 232001)
0 引言
由于电力系统中的电能常常受到很多污染,人们为了更安全地使用电能就需要对受影响的电能信号进行检测[1],分析各种类型的扰动信号的频率、幅值以及持续时间.这些扰动信号进行采样收集后,往往伴随各种噪声的污染,使人们无法判断其属于哪种扰动类型,那么对采样信号进行去噪处理,使其最大程度上还原出原始信号就显得极为关键[2-4].小波变换由于对突变以及非平稳信号具有较强的适应性分析,如今已广泛应用于电能扰动信号的检测与识别当中.而基于小波变换的扰动信号去噪也成为当下的研究热点,常见的小波去噪方法有;小波阈值去噪法、小波系数相关性去噪法、模极大值去噪法等[5].其中应用最广泛的是阈值去噪算法.由D L Donoho等[6]提出的传统的软硬阈值降噪法,小波分解层数与小波基难以确定,同时硬阈值函数在处理信号上会出现阈值处不连续性,呈现“一刀切”现象.软阈值函数则出现边缘模糊、固定偏差等情况,使其去噪效果都差强人意.综上所述,在剖析了传统软硬阈值去噪的基本原理及其函数方程后,理解各自存在的优缺点,给出了采用自适应阈值门限结合改进阈值函数的去噪算法,在Matlab环境下模拟仿真电能扰动信号,分别使用传统和改进的算法进行去噪对比实验,最后从信噪比和均方根误差两方面综合分析,证明了改进的去噪方法能够有效克服传统去噪的缺陷[7].
1 小波阈值去噪原理
假设在接收端采集到的一维含噪信号为
s(t)=f(t)+n(t),
(1)
其中,s(t)表示含有噪声的采集信号;f(t)表示理想状态下的原始信号;n(t)表示包括噪声、脉冲等的干扰信号.研究表明,噪声信号往往以高频信号的形式出现,而原始信号一般为低频且平稳的信号[8].这样的区别就给小波去噪提供了依据.而去噪就是将采集信号s(t)中的原始信号f(t)及干扰信号n(t)拆分开,通过阈值量化将干扰信号n(t)尽可能剔除[7],最后通过小波重构最大程度上还原出原始信号.小波变换去噪的具体实现过程如图1所示.但其中需要注意的是,不光是阈值门限和阈值函数的选取会对去噪结果产生影响,小波变换去噪法在选择什么样的小波基分解以及具体分解多少层上均会影响最后的去噪结果.本文在这4个方面均有介绍并都进行了实验验证,着重阐述前两部分,即改进阈值处理部分.

图1 小波阈值去噪流程图
2 传统阈值去噪算法
2.1 阈值的选取
去噪阈值门限的量化选取会对最后的去噪结果造成影响.当阈值选取过小时,干扰信号的小波系数会大于所设定的阈值,从而导致算法判断其为有用信号而被保留下来;当阈值选择过大时,则一些有用信号因为低于所选定的阈值,而被当成干扰信号给过滤掉.
目前传统的阈值选择方法可以分为以下4种:
(1)无偏风险估计阈值(rigrsure)
先将信号s(i)中包含的所有元素取绝对值,并根据从小到大进行排序,再将各个元素求平方,则新的元素序列为
f(k)=
(sort(|s|))2(k=0,1,…,N-1).
(2)
然后对阈值为f(k)的第k个元素取平方根,
λk=
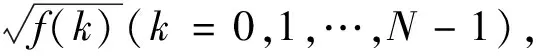
(3)
则该阈值所产生的风险为
Rish(k)=
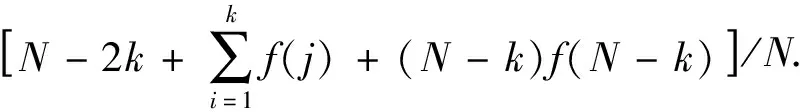
(4)
在得到风险曲线Rish(k)后,取最小风险点所对应值kmin,即rigrsure阈值为
(5)
(2)固定阈值(sqtwolog)
(6)
式中,N为信号长度.
(3)启发式阈值(heursure)
它是由rigrsure阈值和sqtwolog阈值折中而来的,当信噪比SNR较大时,它会自适应选择rigrsure阈值,当SNR较小时,会选择sqtwolog阈值.
(4)极大极小阈值(minimaxi)
(7)
N为信号长度.
2.2 小波阈值函数
传统的小波阈值函数分为硬阈值和软阈值函数.其中硬阈值函数表达式为
(8)
对应的函数图像如图2所示.上式中λ为给定的阈值门限,当经过尺度函数分解得到的小波系数绝对值大于等于阈值门限时,其值保持不变;当绝对值小于阈值时,则令该情况为零.
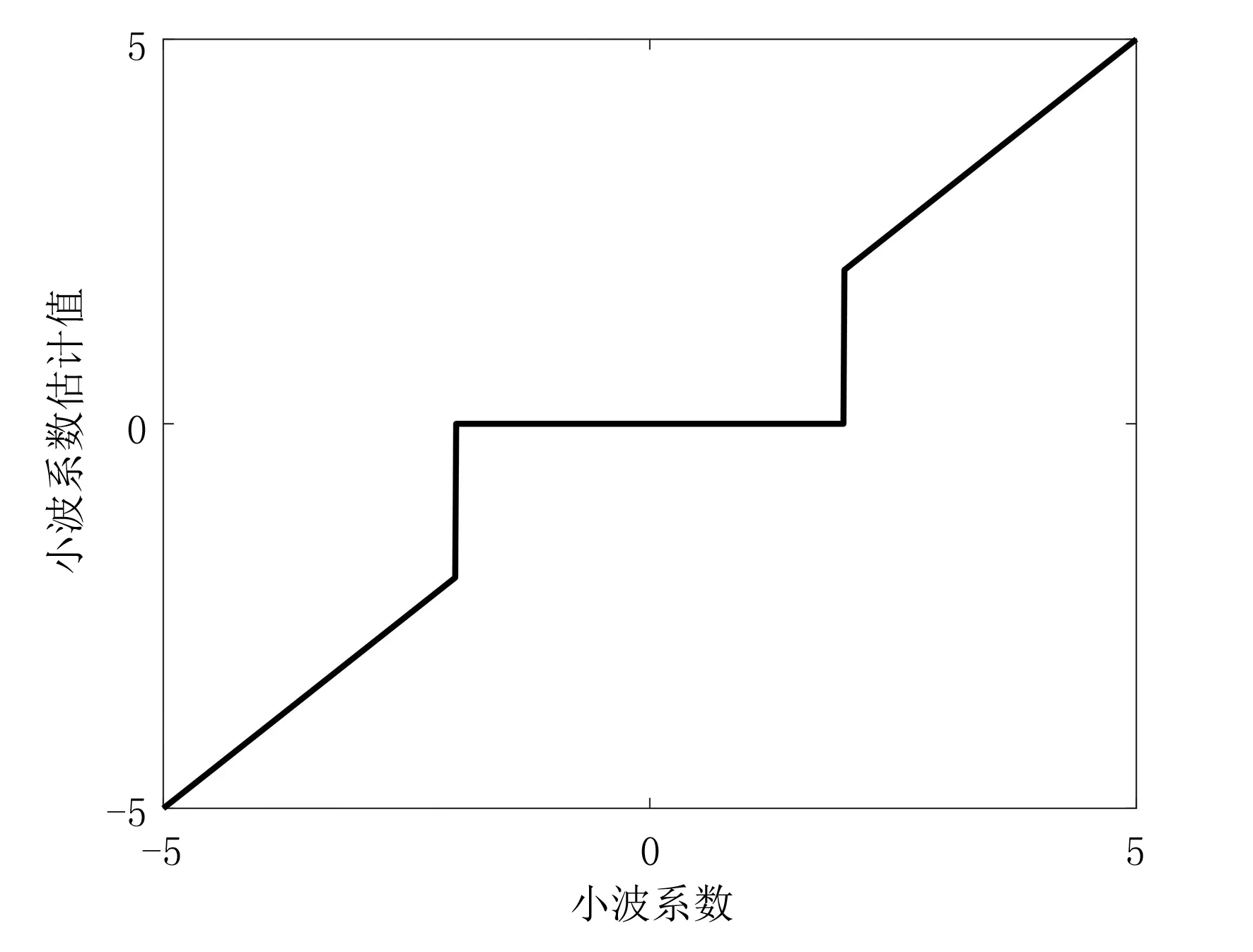
图2 硬阈值函数图
软阈值函数表达式为
(9)
其中:λ为给定阈值;sgn()为符号函数.其对应的函数图像如图3所示.
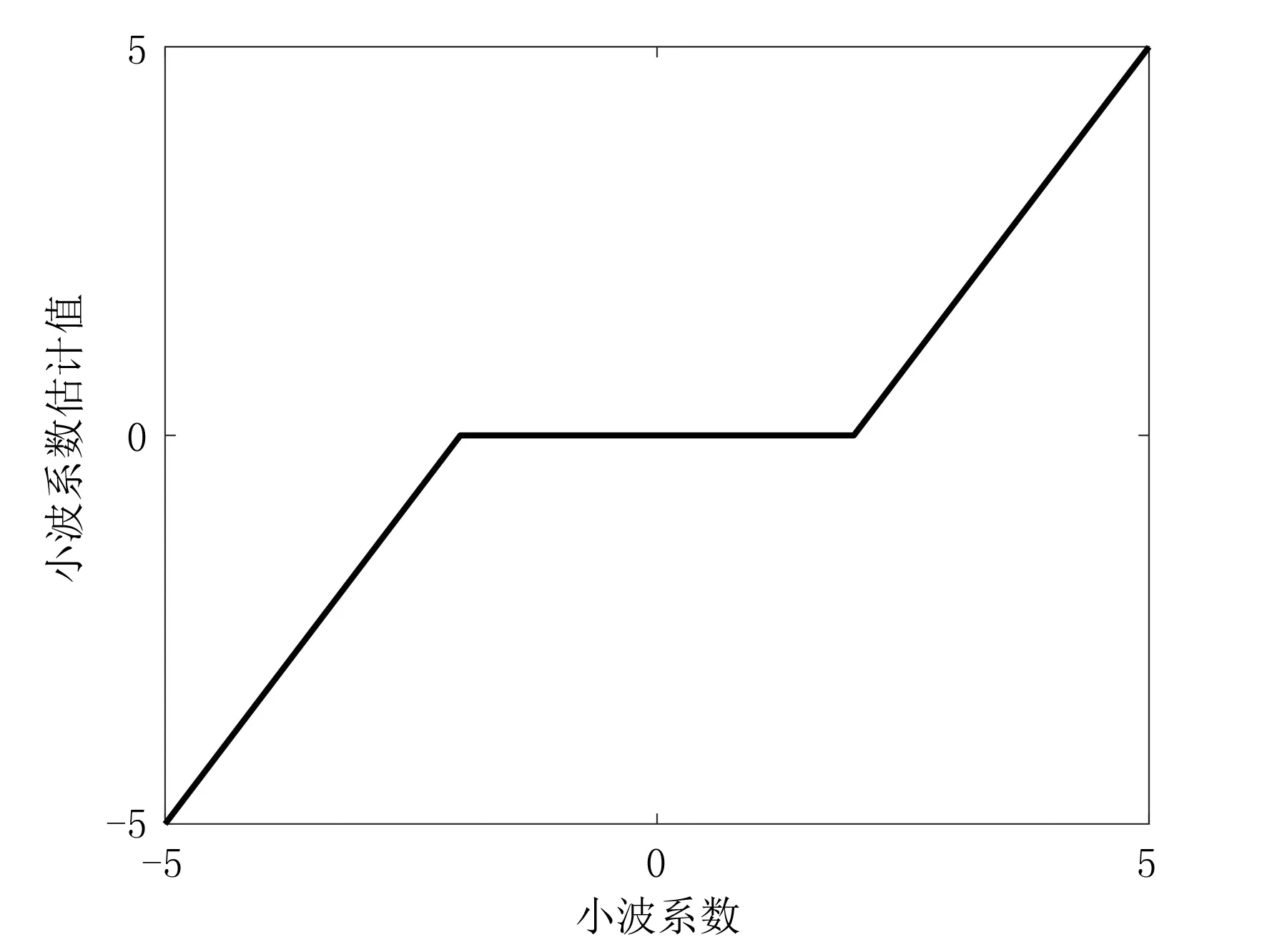
图3 软阈值函数图
综上所述,经由函数图像以及表达式能够发现硬阈值函数在对含噪声信号进行去噪时可以很好地保留其主要特征.但是因为硬阈值函数在所选阈值±λ处具有间断点,从而导致函数不连续,直接造成了重构后的信号波形产生震荡.而软阈值函数则解决了硬阈值函数不连续的缺陷,使处理后的信号波形变得平滑且连续,但由于所得到的小波系数估计值与原小波系数之间存在固有偏差,从而造成重构的信号出现波形失真.
3 改进的小波阈值和阈值函数
3.1 改进小波阈值
第二节内容介绍了4种传统阈值选取规则,可以发现上述方法都没有考虑到噪声的方差,且对于每一层分解所用的小波系数都采用同一阈值估计,这样经过分解重构后的小波信号会发生严重失真.本文在考虑上述问题后,采用改进传统阈值量化规则的新阈值,其表达式为
(10)
式(10)中噪声方差σ由式(9)得到.
σ=median(|cD|)/0.6745,
(11)
其中,cD为处理后的高频小波系数.
式中λ可随分解层数n的变化而发生改变,满足自适应调整阈值的条件,使得分解重构后的小波信号得到更好的还原.
3.2 改进阈值函数
由上文分析可知,软、硬阈值函数在处理噪声信号上均存在缺陷,为此本文改进了阈值函数,使其能够更好地剔除干扰信号.其数学表达为
(12)
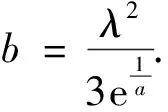
由式(12)可得出新的小波阈值函数具有以下特征:
(1)该函数克服了硬阈值在±λ附近存在间断点的缺点,整体是一个连续函数.
(2)在|wj,k|≥λ区间内,新函数能够快速逼近硬阈值函数,从而改善了软阈值函数存在的固有偏差问题.
(3)指数函数和调节因子的引入使得改进后的新函数自适应能力相较于传统函数有了很大提升,当含噪信号经去噪重构后得到的波形毛刺较多不平滑,可以增大调节因子a的取值,若情况相反则可减少其取值.
新函数对比传统软、硬阈值函数的图像如图4所示.
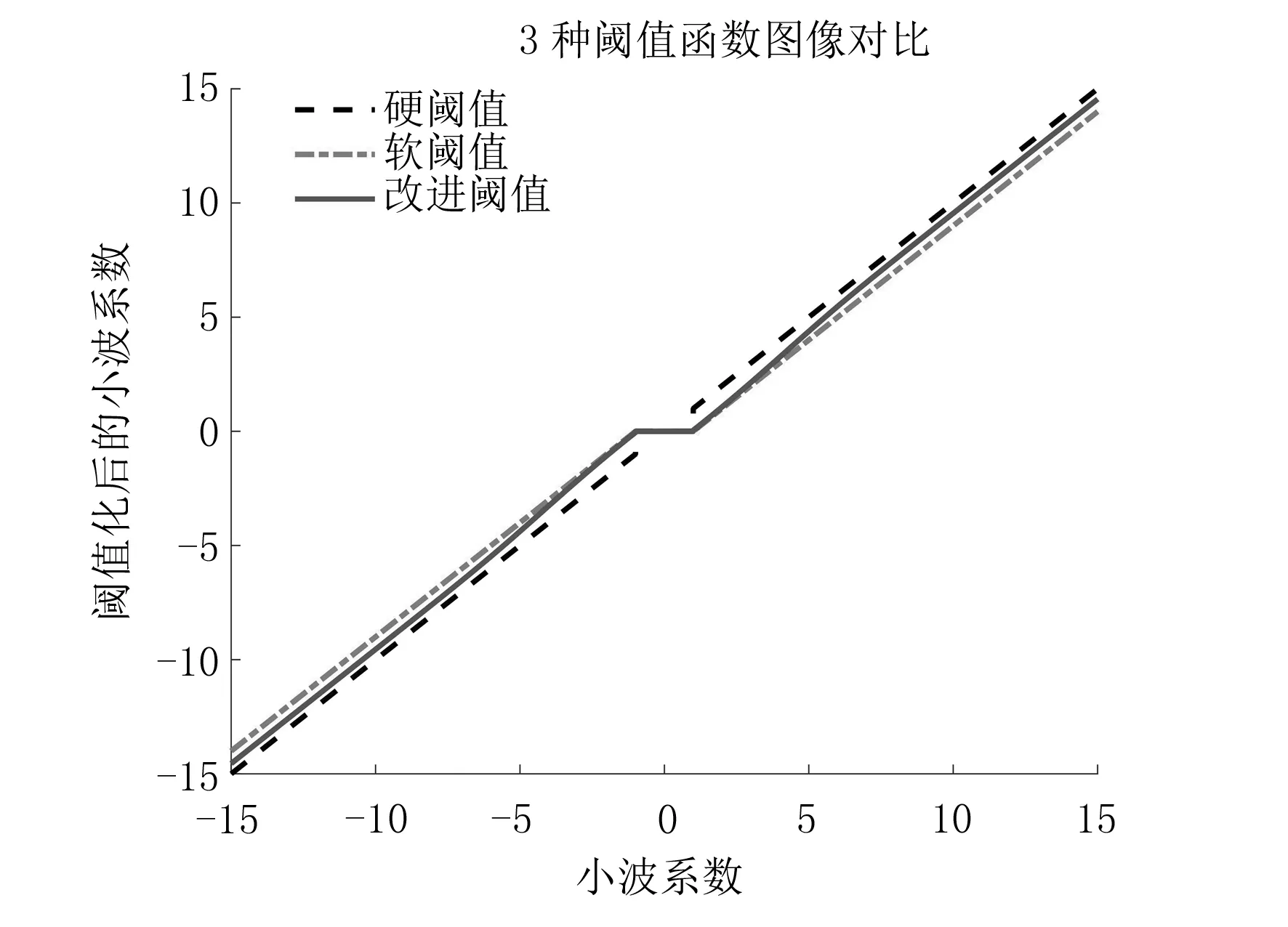
图4 3种函数图像对比图
4 实验仿真
本文依据IEEE对电能质量扰动信号的定义,利用代数方程式在Matlab仿真软件中随机生成电能质量扰动的信号波形,这里以电压暂降的扰动类型举例,其数学模型为
{1-c[u(t-t1)-u(t-t2)]}sin(w0t),
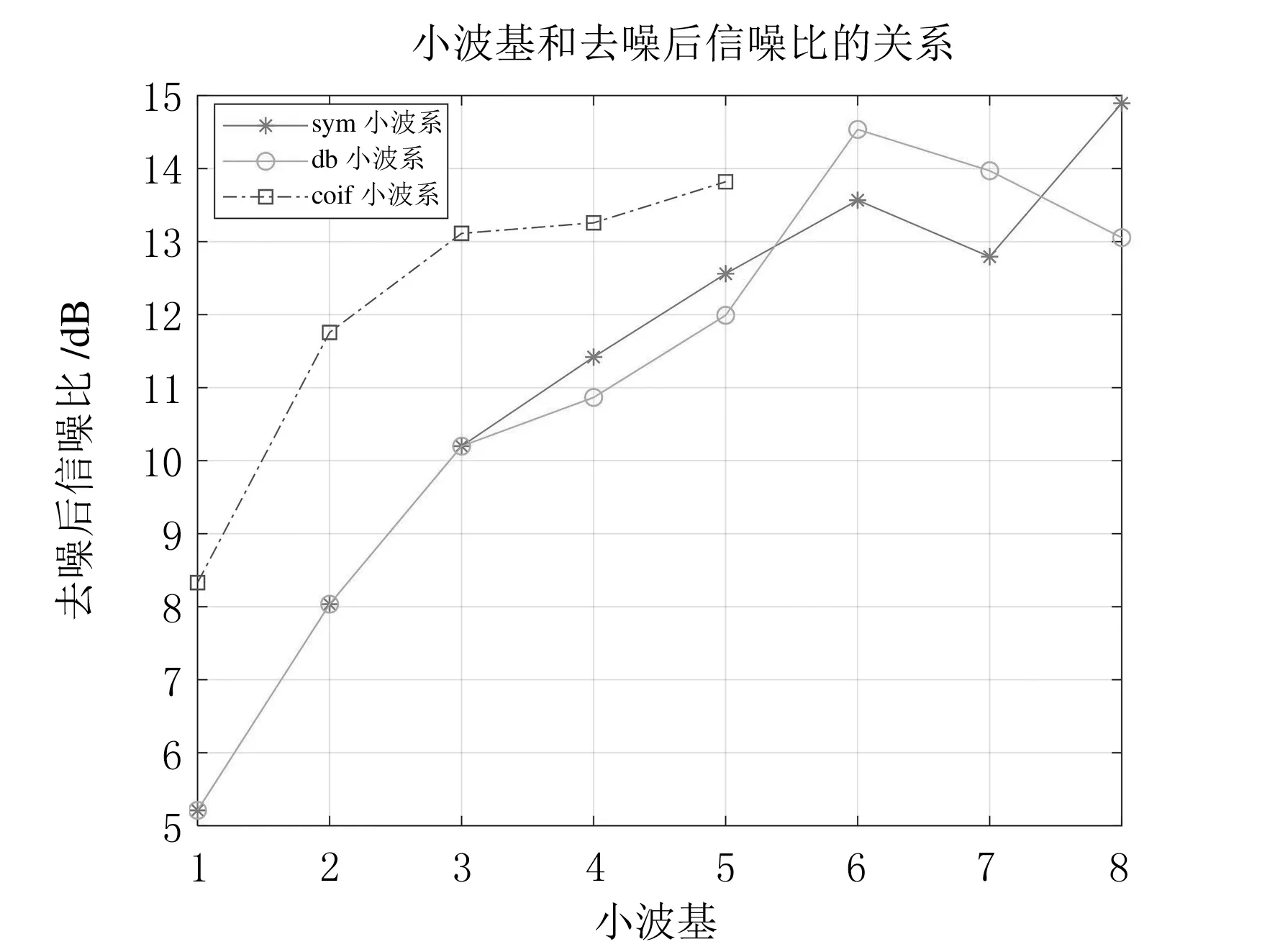
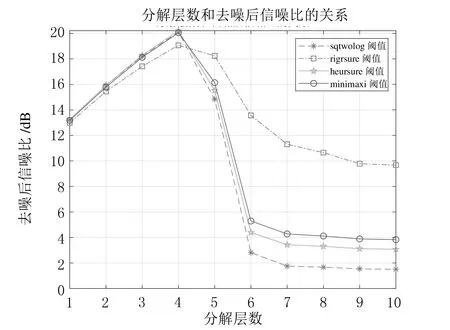
c=0.9~1.0,T (13) 其中:c为电压幅值. 接下来为原始扰动信号添加SNR为10 dB的高斯白噪声,信号的取样频率为50 Hz,取样点数为1001.其原始信号以及染噪波形如图5所示. 图5 原始及染噪信号波形图 为了更客观地对比去噪算法的优劣,这里引入了信噪比(SNR)以及均方误差(MSE)作为衡量标准.其计算公式分别为 (14) (15) 其中:s(i)为原始信号;y(i)为去噪后的信号. 由式(14)、式(15)可知,若信号经去噪后得到的信噪比SNR值越大,均方根误差MSE值越小,则说明去噪算法性能越优良. 由于在使用小波去噪时,其小波基的选取以及分解层数不是自适应确定的,这也是小波变换的缺点,这里通过调用并计算sym小波基、db小波基以及coif小波基与去噪后信噪比的关系,经过30次试验对比,结果显示最优小波基为sym8小波基,其函数曲线图如图6所示.通过比较4种传统阈值与去噪后信噪比的关系计算出最佳分解层数,经过30次仿真实验,其函数图像如图7所示,可以看出最佳分解层数为4层. 图6 小波基和去噪后信噪比的关系图 图7 分解层数和去噪后信噪比的关系图 在确定完最优小波基和最佳分解层数后,开始进行实验对比仿真.这里拿软、硬阈值函数与4种传统阈值相互结合,得到8种组合结果,分别仿真出去噪重构后的波形,与改进后的阈值去噪法相对比,其仿真结果如图8所示. 由图8可知,9种仿真结果总体上都能保留大部分有用信息,4种传统阈值与软阈值结合去噪后的效果明显优于硬阈值,从直观上很难分析出仿真结果的好坏.接下来针对这9种去噪方法进行定量分析,使用上文介绍过的信噪比和均方误差作为衡量算法好坏的标准,随机生成30组含10 dB高斯白噪声的信号进行实验,取平均值,具体结果如表1所列. 由表1可以看出,4种传统阈值与软阈值函数结合的去噪效果在定量标准下是优于与硬阈值结合的,而改进后的去噪算法信噪比最高,均方误差最小,从结果上看要明显优于传统的8种算法组合. 表1 9种去噪算法定量比较 小波去噪在一维信号噪声处理方面具有广泛的应用.文中在解决扰动信号噪声问题上较传统方法具有以下3个优点:第一,通过算法可以自适应确定最优小波基和分解层数;第二,从MATLAB的仿真结果上看,改进后的去噪算法进一步优化了传统算法,不管在图像还是定量分析上都具有显著的提高;第三,改进后的阈值去噪算法在应用于电能扰动信号去噪后能够较好地保留扰动波形的特征信息,从而为后续研究的扰动突变定位、突变幅值以及扰动持续的时间等提供可靠的研究依据.综上所述,证明了改进后的算法是要优于传统去噪算法.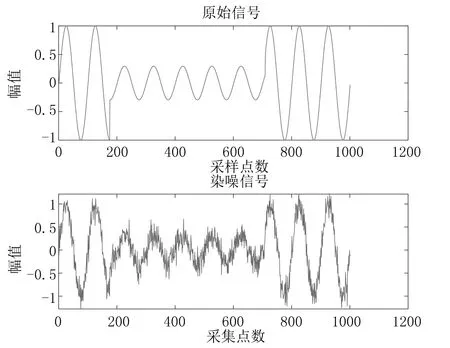

5 结语

