基于ARIMA模型对江苏省GDP的预测
查 华,石 舢
(1.南京审计大学 统计与数据科学学院,江苏 南京 210031;2.喀什大学 数学与统计学院,新疆 喀什 844000)
0 引言
GDP数据的大小从一个角度反映了这个国家或地区的经济状况,因此预测和分析GDP数据未来的走势,具有非常重要的理论意义和现实意义.GDP数据受多方面的因素影响.江苏省地区生产总值自改革开放以来持续增长,江苏省GDP总量一直位居全国前几位.本文以通过江苏省统计年鉴获取了1975-2020年GDP数据为样本,以1975-2017年江苏省GDP数据为训练集,以2018-2020年江苏省GDP数据为测试集,通过相对性误差分析,构建了可信度较高的ARIMA模型.对江苏省未来2年的GDP做出了预测,预测的结果为江苏省制定经济决策提供了参考.
随着近些年来对经济的研究热度持续上升,GDP是在经济研究中的一个重要指标.目前对GDP数据的预测方法众多,国内目前也有不少学者通过不同的预测方法对GDP数据进行了预测,也获得了不同预测效果.朱佳俊[1]通过选用1978-2018年我国的GDP数据,运用统计分析R软件先后构建了ARIAM模型、BP神经网络模型、组合预测模型,最终通过构建预测效果较好的改进组合模型对我国未来3年的GDP进行了预测.严彦文[2]通过对1975-2015年GDP数据进行分析,构建了ARIMA(1,1,1)模型,对山东省未来五年的GDP进行了预测.沈秋彤[3]以1978-2013年辽宁省的GDP数据为样本,构建了ARIMA(1,1,1)模型并对辽宁省2012-2014年GDP数据进行了预测,经过对比发现2012和2013年实际GDP和预测GDP相对误差都控制在5%以内.同时对辽宁省统计局当年发布的2014年GDP数据和模型预测数据进行对比,发现预测误差控制在5%以内,模型短期预测效果较好.宋平和邱燕玲[4]选取1993-2016年青海省GDP数据,通过构建ARIMA、最小二乘模型和逐步回归3个模型分别对青海省2015年和2016年两年GDP数据进行预测,得出了3个模型都有较好的预测效果,同时ARIMA模型短期预测效果较好,在预测10年以及时间更长的长期预测效果较差.本文选取江苏省1975-2020年GDP数据,通过spss软件和python软件数据分析的功能构建ARIMA模型,对江苏省未来2年的GDP数据做出了预测.
1 理论基础
1.1 ARIMA模型理论基础
ARIMA是差分自回归移动平均模型的英文缩写,其中AR表示的是自回归模型,MA表示的是移动平均模型,I表示的是差分[5].它针对的是平稳的时间序列模型.然而在现实生活中绝大多数时间序列都是非平稳的.因此可以对数据进行差分,使其转化为平稳的时间序列,再用ARIMA模型对其数据进行建模和预测.ARIMA模型是根据过去不同时期数据的相关性,可以进行有效和精准的短期预测,它弥补了AR和MA进行预测出现的参数过多问题,在短期预测领域具有广泛的应用.它的基本形式如下:
Φ(B)(1-B)dyt=Θ(B)εt,
E(εk,εt)=0,k≠t,E(εt)=0,Var(εt)=σ2,
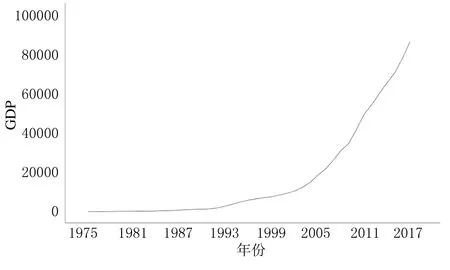
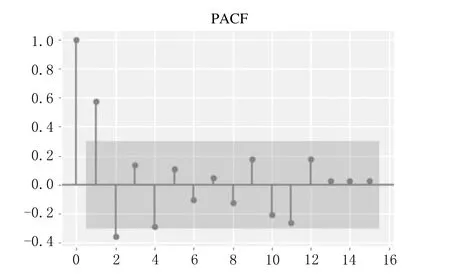
E(εt,yk)=0,∀k ARIMA模型是由AR(自回归)模型和MA(移动平均)模型经过差分构成的组合模型,一般写成ARIMA(p,d,q).p和q分别为自回归阶数和移动平均阶数,d表示差分的次数,一般可以通过几阶差分将不平稳的序列转化为平稳的序列,一般差分的阶数不超过3阶.上述公式中{yt}表示需要预测的时间序列;Φ(B)=1-φ1B-φ2B2-…-φpBp,表示模型的自回归多项式;以及Θ(B)=1-θ1B-θ2B2-…-θqBq,表示为模型的移动平均多项式;{εt}则为白噪声序列,d表示差分的次数[5]. 在对ARIMA模型理论相关知识了解的基础上,用ARIMA模型进行建模预测就变得非常容易了.具体建模流程如下所示: (1)首先需要对需要拟合的样本数据进行平稳性检验. (2)若拟合的样本数据不是平稳数据,则需要进行差分使其平稳化.否则进行下一步. (3)对平稳的样本数据进行白噪声检验,若是白噪声数据,则建模结束;否则进行下一步. (4)对平稳非白噪声的样本数据建立ARIMA模型. (5)模型的优化和应用. 具体的ARIMA建模流程图如图1所示. 图1 ARIMA建模流程图 本文以江苏省1975-2017年的GDP数据作为训练集,以2018-2020年的GDP数据作为测试集构建了ARIMA模型,并预测了江苏省未来2年的GDP数据.1975-2020年的GDP数据均来自于江苏省统计局网站所发布的江苏省统计年鉴,所有GDP数据如表1所列. 表1 1975-2020年江苏省GDP数据 单位:亿元 一般在生活中得到的原始时间序列数据是非平稳的,所以要对数据进行差分或者取对数运算,使原始时间序列数据变成平稳时间序列数据.江苏省1975-2020年GDP数据,选取了1975-2017年数据为训练集,2018-2020年数据为测试集,通过时序图以及平稳性检验发现是非平稳的,时间序列图如图2所示. 图2 江苏省1975-2017年GDP时序图 经过对GDP数据取对数和一次差分后,通过观察时序图可以看出数据变成了平稳时间序列数据,通过取对数和一阶差分后的GDP数据趋势基本消除,但是这并不能够精准地判断该数据为平稳时间序列.对GDP数据取对数和一次差分的时间序列图如图3所示. 图3 江苏省GDP数据取对数一阶差分后时序图 接下来将通过更为严格的单位根检验来进行判断. 通过单位根检验发现p值为0.000 752,分别大于显著性水平为1%和5%以及10%所对应的临界值,可以判断不存在单位根,可以判断出该数据为平稳时间序列.ADF检验结果如表1所列. 表1 取对数后且一阶差分后的GDP序列ADF检验 同时使用python软件对该组数据使用Q检验进行了白噪声检验,结果返回统计量和p值,发现p值全部都小于0.05,表明该平稳序列不是白噪声. 在通过平稳性处理的过程中,模型中的d可以确定为1,模型中的另外两个参数p和q通过观察ACF和PACF图来确定.使用python软件绘制的ACF和PACF图如图4和图5所示. 图4 江苏省GDP取对数一阶差分后序列自相关图 图5 江苏省GDP取对数一阶差分后序列偏自相关图 从图中可以看出,自相关图经过1阶延迟之后,ACF均落在于两倍的标准差范围之内.同时取值围绕0上下波动,呈现出截尾性质.而PACF衰减到0的速度比较慢,呈现出拖尾的性质.初步可以判定拟合MA模型. 但是通过ACF和PACF图对模型进行定阶主观性较强,最后通过AIC和BIC准则来确定.最终通过使用python软件进行数据分析,得出当p=0,q=1时,AIC值和BIC值均取得最小值.最终模型确定为ARIMA(0,1,1),模型统计和参数估计结果如表2、表3所列. 表2 模型统计 表3 ARIMA 模型参数 表2中可以看出相关系数为0.998 714,说明模型的拟合效果较好.同时p值为0.995 302,大于显著性水平0.05,说明残差序列为白噪声.同时还没有离群值的出现,反映出模型整体拟合的效果不错.从表3的参数估计结果来看,p值远远小于显著性水平0.05,说明模型的参数都是显著的,通过了参数的显著性检验.最终的预测模型确定为ARIMA(0.1,1)模型. 通过选取江苏省1975-2020年GDP数据为训练集,建立了ARIMA(0,1,1)模型,同时预测了2018-2022年江苏省GDP数据,预测值见表4所列. 从表4可以看出模型预测的相对误差均在10%以下,平均相对误差为3.75%,整体预测效果较好.同时也给出了江苏省未来2年的GDP数据分别为109 505.67亿元,123 192.63亿元.但是随着预测年份的增加,预测的GDP数据误差也渐渐变大.也反映出ARIMA模型适合做短期预测,不适合进行长期预测. 表4 2018-2022年江苏省GDP预测值与实际值对比 单位:亿元 本文通过选取江苏省1975-2017年GDP数据为测试集,2018-2020年GDP数据为验证集.构建了ARIMA(0,1,1)模型,预测了江苏省2018-2022年的GDP.可以看出模型在验证集上表现出较好的预测效果,平均相对误差在5%以下.最后从结果可以看出,未来2年江苏省GDP呈现出稳步增长的趋势,为当地经济决策者作出经济决策提供了一定的参考.同时随着预测年份逐渐增加,预测精度也发生了下降,也反映出ARIMA模型适合短期预测.尤其是2020年江苏省GDP预测值出现了超过5%的误差,也有可能和2020年出现的新冠疫情有关.1.2 ARIMA模型建模流程
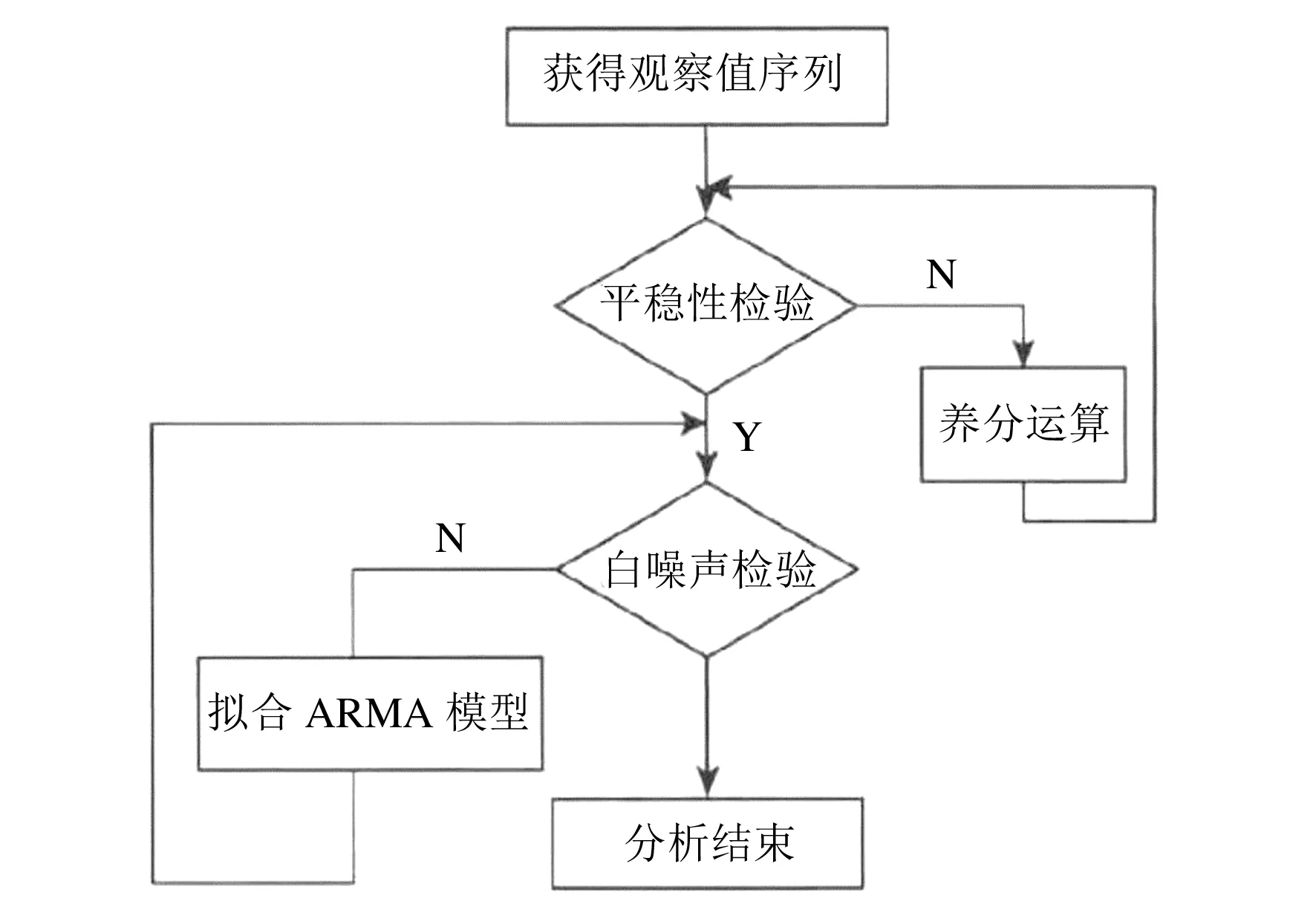
2 实证分析
2.1 数据来源

2.2 平稳性检验及处理
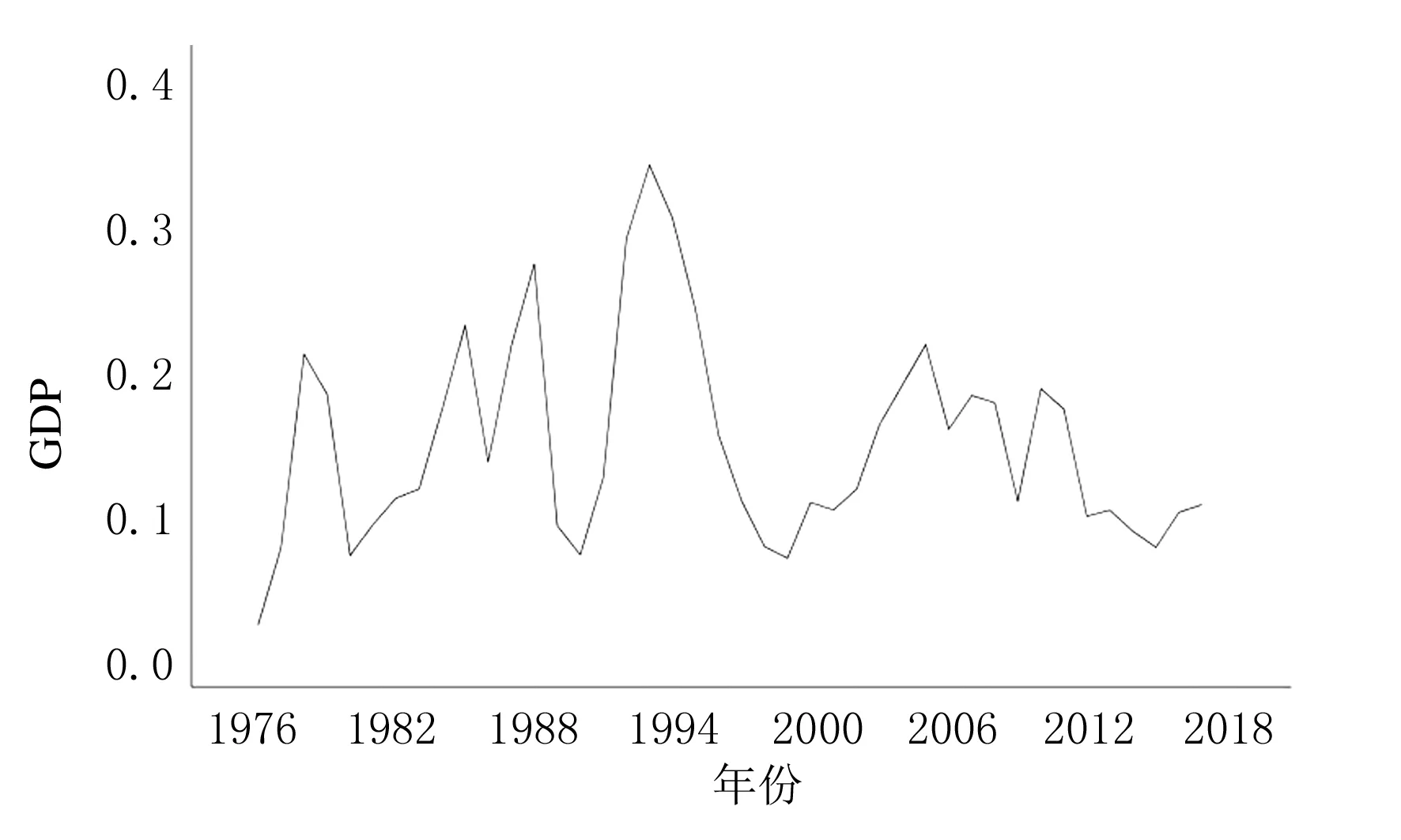

2.3 ARIMA模型的建立及估计



2.4 ARIMA模型预测

3 结语

