机械臂逆运动学的带修复策略自适应差分进化求解*

李志敏

(无锡工艺职业技术学院机电与信息工程学院，无锡 214200)

0 引言

冗余机械臂逆运动学求解问题具有非线性、高耦合性等特点，因此逆运动学求解存在较大困难。冗余机械臂逆解的精度和优劣，将直接决定机械臂末端执行器的定位精度、驱动耗时和耗能[1]，因此研究机械臂逆运动学求解问题具有较大理论价值和实用价值。

机械臂运动学逆解是指根据给定的末端执行器位姿，求解对应的关节角空间点。求解方法可以分为三类，分别为几何法、代数数值法、智能搜索法。几何法依据机械臂的机械结构，使用几何知识对逆运动学进行求解。胡奎等[2]引入了臂角变量的概念，将关节角限位与臂角可行范围进行映射，并将该映射关系进行线性展开，得到了一种冗余机械臂逆运动学求解方法。FARIA等[3]通过最小化当前位置和自运动范围边界，实现避关节限位和避奇异，同时求出运动学逆解。代数数值法是指使用增广雅可比矩阵、伪逆法、梯度投影法等进行逆运动学求解。东辉等[4]使用傅里叶变换和卷积定理构造非线性空间密度函数，使用迭代法求解该密度函数，从而得到运动学逆解。WAN等[5]在最小二乘范数法中引入了弹性场函数，从而提出了改进最小二乘范数法的逆运动学求解方法。基于智能搜索算法的求解思路为，将逆运动学求解问题转化为搜索问题，包括粒子群算法、遗传算法等。谢习华等[6]提出了权值自适应差分进化算法，并使用映射关系解决边界约束问题，与传统算法提高了求解精度和速度。BAYATI[7]将布谷鸟算法与帝国主义算法混合，将其应用于机械臂逆运动学求解，求解性能好于单独算法。以上研究方法在各自设置场景下均取得了较好的结果，但是仍有两个问题需进一步解决：一是进一步优化算法的搜索能力，算法搜索能力决定了问题求解深度；二是对于约束优化问题，约束条件的转化仍需进一步研究。

针对冗余机械臂逆运动学求解问题，本文以位姿精度为前提，以关节角变化量为优化量。提出了带修复策略自适应差分进化算法的求解方法，在保证逆解精度基础上，实现了关节角变化量最小化的目标。

1 问题描述与建模

1.1 研究对象

本文以KUKA LBR iiwa7自由度冗余机械臂为研究对象，该机械臂具有7个自由活动关节，该机械臂的简易模型如图1所示。

图1 机械臂简易模型

此机械臂运动学的D-H参数如表1所示，表中ai为连杆长度，αi为连杆扭曲角度，di为连杆偏置，θi为关节转角。

表1 机械臂D-H参数

1.2 问题分析与模型

在机械臂运动学逆解问题的研究中，一般以机械臂末端的位置误差和姿态误差最小为求解目标。但是除了考虑求解的精度外，关节角的变化量也至关重要。以图2所示情况为例，图2中A点为起点位姿，B点为终点位姿，其中B点位姿对应2种关节角组合。关节角变化量与机械臂耗能、耗时具有直接关系，因此从关节角变化量的角度讲，点B应当选择关节角组合1，而不是关节角组合2。

图2 逆运动学多解举例

一般来说，7自由度冗余机械臂末端执行器的位姿点均对应无数个关节空间点，因此存在运动学逆解选择与优化的问题。按照上述分析，本文将冗余机械臂逆运动学求解的优化模型设置如下。

优化目标为关节角位移之和最小，即：

(1)

式中，y为优化目标函数；N为位姿点数量。

约束条件包括两个方面，一是关节角运动范围约束，二是末端执行器位姿误差应在一定误差范围内。

约束条件1：所有关节角的活动范围都应在约束范围内，描述为：

θimin≤θi≤θimax

(2)

式中，θimin为关节i的最小关节角；θimax为关节i的最大关节角。

约束条件2：末端执行器位姿误差应在一定误差范围内。本文使用末端执行器质心位置坐标(x,y,z)代表末端执行器位置；姿态表示方法较多，包括欧拉角法和四元素法等，为了计算简单和叙述方便，使用四元素(i,j,k,v)表示末端姿态。对于关节空间点θ，使用正运动学方程得到的末端执行器位姿表示为：

(3)

式中，R3×3为3×3矩阵，表示末端执行器姿态；P1×3=(x,y,z)T表示末端执行器位置；03×1为零矩阵。

将期望的末端执行器位置记为Pex=(xex,yex,zex)T，则位置误差的约束条件为：

(4)

式中，Ep表示位置误差；‖‖表示欧氏距离；Δp表示位置误差阈值。

(5)

则末端执行器姿态误差的约束条件为：

Er≤Δr

(6)

式中，Er表示姿态误差；Δr表示姿态误差阈值。

结合式(1)、式(4)、式(6)，即可得到机械臂逆运动学求解的优化模型。

1.3 正运动学方程

机械臂正运动学求解一般通过旋转和平移实现。可以由以下几个步骤实现：

步骤1：建立关节坐标系，以关节i转向为Zi轴向；Xi轴向为Zi轴与Zi+1轴的垂直方向，并由Zi轴指向Zi+1轴；Yi轴向根据右手准则确定，如图3所示。

图3 机械臂坐标系

步骤2：使用RX(α)表示沿X轴旋转α角，RY(β)、RZ(γ)具有类似含义；PX(d)表示X轴正向平移距离d，PY(t)、PZ(a)具有类似含义。则坐标系i到坐标系i+1的旋转矩阵可表示为：

(7)

2 带修复策略的自适应差分进化算法

2.1 差分进化算法

差分进化算法主要包括算法初始化、交叉、变异、选择等操作。其中初始化使用随机初始化方法，选择使用一对一贪婪准则，即当子代优于父代时选择子代进入下一代，当父代优于子代时选择 父代进入下一代。在此着重介绍变异和交叉操作。

DE/rand/1的变异方式为：

(8)

DE/rand/2的变异方式为：

(9)

式中，r1、r2、r3、r4、r5为种群中的5个任意个体，且r1≠r2≠r3≠r4≠r5。

DE/best/1的变异方式为：

(10)

DE/best/2的变异方式为：

(11)

DE/target-to-best/1的变异方式为：

(12)

(2)交叉操作。差分进化算法的交叉操作是在染色体维度方面依据交叉因子进行交叉互换，为：

(13)

式中，CR为交叉因子，取(0,1)之间的值；rand为(0,1)间的随机数。

2.2 自适应差分进化算法

在第2.1节给出了多种变异策略，但是不同策略的适用情况不同[8]。比如，DE/best/1、DE/best/2和DE/target-to-best/1在解决单峰问题时，收敛性好且能快速找到最优值，但是求解多峰问题时容易陷入局部极值；DE/rand/1和DE/rand/2的变异策略与此相反，适用于多峰问题，但是求解单峰问题时收敛性较差。

对于实际待解决的问题，一般情况下难以掌握该问题的全部性质，因此无法确定一个适用的变异策略。为了解决这一问题，本文提出了变异策略自适应确定方法。具体操作方法如下。

从种群中随机选择染色体作为测试染色体，在算法更新至k代时，第i个变异策略生成的个体被选为下一代的个数记为si,k，无法被选为下一代的个数记为fi,k，则第i种变异策略的成功得分Qi,k为：

(14)

式中，ε为一个较小值，本文取ε=0.01，防止出现Qi,k=0的情况。则算法迭代至k代时使用第i种变异策略的概率为：

(15)

算法依据式(15)，按照轮盘赌规则确定最终使用的变异策略。经过以上设计，算法可以根据问题特点自适应改变和选择变异策略，使算法的变异策略可以根据问题特点自适应变化。

2.3 针对约束条件的修复策略

针对带约束的优化问题，当前常用方法包括可行准则法、罚函数法等。本文以DE/best/1变异策略为例对上述方法进行分析。使用图4所示情况说明，假设图中T点为位置最优点，点A和点C为第k代个体，经过变异和交叉后k+1代分别为B点和D点。

图4 约束条件处理方法分析图5 修复策略核心思想

若使用可行准则法，B点不在可行域内，因此染色体B不会进入下一代；而点D函数值优于点C，且点D在可行域内，因此点D会进入下一代。但是从实际上讲，点B的搜索方向更优，却因为可行域被放弃。罚函数也具有类似的缺陷，该方法得到的个体并不能维持自适应差分进化算法的最优搜索方向。

为了保持自适应差分进化算法较优的搜索方向，针对约束条件处理问题，本文提出了带伸缩因子的修复策略。修复策略的核心思想如图5所示，图中A点为第k代个体，经过变异和交叉后k+1代分别为B点，当B点在可行域外时，使用伸缩因子将其沿原搜索方向映射到可行域中距离点B最近的点C。

具体实现方法为：当点B超出可行域时，构造一个子问题为：

(16)

式中，g(x)≤0为原不等式约束；k0为映射伸缩因子。式(16)含义为在原方向AB上搜索距离点B最近的点C。

3 仿真与验证

3.1 仿真设置

为了对上述逆运动学求解方法进行验证，以螺旋曲线为例进行逆运动学求解，螺旋曲线函数为：

在该螺旋曲线上等步长均匀选取100个点作为轨迹点，末端执行器姿态根据任务需要设置为表2所示情况。

表2 末端姿态设置

带修复策略的自适应差分进化算法参数设置为：最大迭代次数为200，缩放因子F=0.7，交叉因子CR=0.9，染色体规模为70。位置误差阈值Δp=10-4mm，姿态误差阈值Δr=10-4rad。

3.2 求解结果与分析

为了验证改进措施的有效性，首先将带修复策略的自适应差分进化算法与带修复策略的传统差分进化算法进行比较，传统差分进化算法参数设置与自适应差分进化算法参数一致。为了对比两种算法的搜索快速性、搜索精度和搜索稳定性，使用两种算法各自独立求解10次，某次的搜索过程如图6所示。

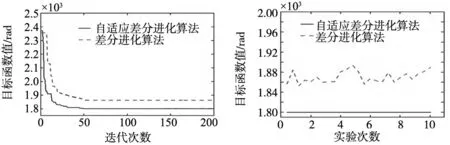
图6 求解的搜索过程图7 求解结果分布

可以看出，差分进化算法和自适应差分进化算法的收敛速度相近，均在迭代至50次左右时目标函数值不再下降。

自适应差分进化算法和差分进化算法各自独立运行10次得到的结果分布如图7所示。

由图7给出的10次结果分布，并结合图6搜索结果可以看出，自适应差分进化算法搜索的结果整体优于差分进化搜索结果；从结果分布稳定性角度分析，差分进化算法搜索的结果存在较大波动，而自适应差分进化算法搜索结果的波动极小。综合以上分析，自适应差分进化算法的搜索精度和稳定性均优于差分进化算法。

为了进一步分析本文方法对逆运动学问题的求解性能，同时使用本文方法、文献[9]、文献[10]方法对上述逆运动学问题进行求解，各自独立运行10次，结果如表3所示。

表3 逆运动学求解结果 (rad)

由表3可以看出，本文提出的带修复策略自适应差分进化算法求解的目标函数值最小，为1.80×103rad，差分进化算法、文献[9]、文献[10]求解的目标函数均值均大于本文方法。从标准差的角度看，本文所提方法在10次求解中均能够得到相对最优解，算法稳定性高于另外几种方法。以上结果和分析验证了带修复策略自适应差分进化算法在逆运动学求解中的优越性。

下面对带修复策略自适应差分进化算法的逆运动学求解精度进行验证，结果如图8所示。

图8 求解点与标准轨迹

经统计，100个轨迹点的逆运动学求解中，最大位置误差为1.2×10-5mm，最大姿态误差为1.6×10-5rad，均满足设置的位姿误差约束。结合图7和图8可知，本文提出的逆运动学求解精度较高，且能够在保证精度前提下，得到角度变化量最小的逆解。以上结果和分析验证了带约束自适应差分进化算法在逆运动学求解中的优越性。

4 结论

本文研究了机械臂逆运动学求解问题，在保证逆解精度前提下，搜索关节角变化量最小的逆解。提出了变异策略自适应变化策略，有效提高了算法的搜索能力。针对约束条件，给出了带伸缩因子的修复策略，解决了约束条件问题。经验证得出以下结论：①带伸缩因子的修复策略可以有效解决约束问题；②自适应变异策略有效改善了差分进化算法的搜索能力；③在保证逆解精度前提下，带修复策略的自适应差分进化算法可以搜索出关节角变化量较小的逆解。