融合ArUco码先验信息的SLAM累计误差消除算法*
刘贵涛,张 雷,徐 方
(1.中国科学院沈阳自动化研究所机器人学国家重点实验室,沈阳 110016;2.中国科学院机器人与智能制造创新研究院,沈阳 110169;3.中国科学院大学,北京 100049;4.沈阳新松机器人自动化股份有限公司,沈阳 110168)
0 引言
双目视觉SLAM(simultaneous localization and mapping)系统通过处理图像序列,可以实时地估计双目相机的位置和姿态。因为双目相机具有成本低廉,安装方便,同时适应室内和室外环境,获取信息丰富等优点,因而被广泛地应用到移动机器人自主导航中。通过将双目视觉SLAM系统前后帧数据关联,可以实时地向机器人输出双目相机的位姿。但是由于噪声的干扰,随着时间增加,双目视觉SLAM系统估计的相机位姿累积误差会越来越大[1],可能最终导致SLAM精度下降甚至定位失败。
针对此问题,目前主流的方法是依靠回环检测及回环校正,消除双目视觉SLAM系统的累积误差。ORB-SLAM2系统[2-4]引入了DBOW2库[5],用于回环检测,消除系统的累积误差。虽然该方法回环的准确性很高,但是回环率很低,即经常在发生回环的地方,检测不到回环。同样是利用DBOW2,PL-SLAM[6]同时对点特征描述和线特征描述进行聚类训练,得到基于点线特征的词袋模型。应用点线特征的模型,虽然定位精度更可靠,但是回环率依然很低。单纯依靠人工特征AprilTag的TagSLAM系统[7]的回环检测方法成功率和准确率很高,可以很好地进行累计误差消除。UcoSLAM[8-9]是一种融合自然特征和人工特征的单目视觉SLAM方法。在存在人工特征的地方,回环检测的成功率和准确率都很高,可以很好地消除视觉SLAM系统的累积误差。虽然回环校正的方法可以有效地消除SLAM系统的累积误差。但是,实际机器人工作场景中存在许多无法回环的情况。在无回环场景下,消除双目视觉SLAM系统的累积误差,有着重要的实际应用价值。因为它不仅会极大地扩展移动机器人的应用场景,还可以大大提高移动机器人的定位精度。
为了解决上述问题,本文提出了一套利用ArUco[10]码先验信息辅助消除累积误差的算法。该算法由下面三个步骤组成,首先,进行ArUco码检测,得到ArUco码在检测图像中的位置;然后,结合ArUco码先验信息和ArUco码在图像中的位置,估计相机在世界坐标系下没有累积误差的位姿;最后,构建图模型,优化全局地图,消除双目SLAM系统的累积误差,得到精确的环境模型。
1 SLAM系统
本文提出的算法以ORB-SLAM2系统为基础框架,新增ArUco码检测模块、相机位姿估计模块和累积误差消除模块。整体系统架构如图1所示,虚线框部分为本文所提方法的贡献。
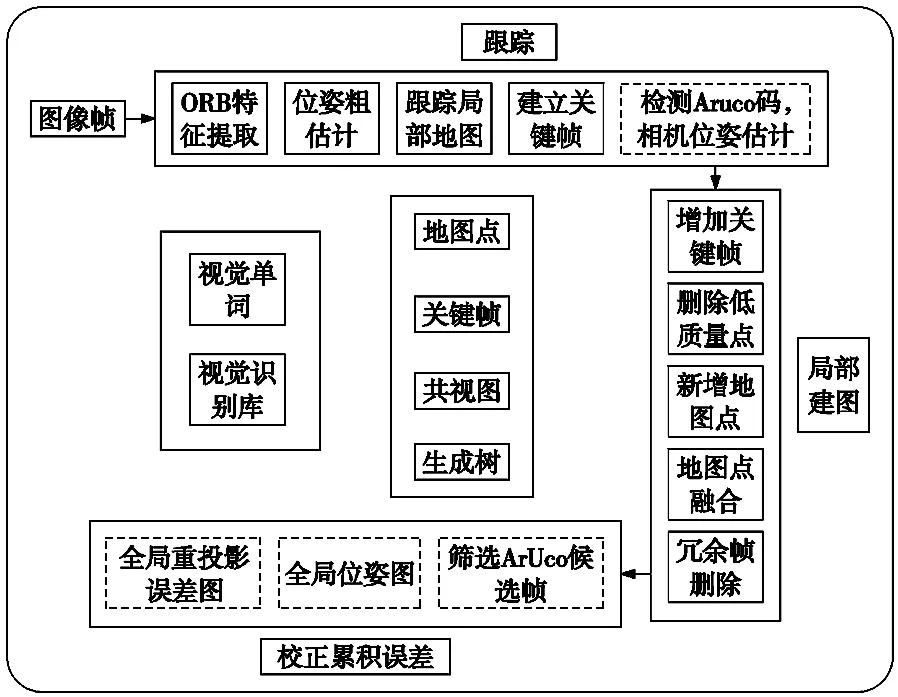
图1 SLAM系统
整个算法包含前端跟踪、后端建图、校正累积误差三个线程,下面分别进行介绍。
1.1 前端跟踪线程
前端跟踪线程接收双目图像数据流。首先,按照参考帧模型或运动模型跟踪3D地图特征点位置,粗略估计相机位姿。之后,跟踪局部地图的所有3D地图特征点,精确估计相机位姿。当图像中跟踪的3D地图特征点数目不足时,建立新的关键帧,生成新的3D地图特征点。
在构造新的关键帧时,系统还会检测该关键帧图像中是否存在ArUco码。在检测到ArUco码后,采用EPNP[11]算法计算相机相对该ArUco码坐标系的位姿变换。之后,结合该位姿变换和ArUco码先验信息计算该关键帧处相机消除累积误差后的位姿,并将其保存。最后,系统将该关键帧传入后端建图线程。
1.2 后端建图线程
后端建图线程接收到新的关键帧后,对该关键帧新建立的3D地图特征点按照一定的策略进行筛选,只保留质量高的点。在此进程中,还会进行三角化左右目图像2D特征点、融合地图、删除冗余关键帧以及局部地图集束调整(bundle ajustment,BA)等工作。最后,后端建图线程将该关键帧传入全局校正线程。
1.3 校正累积误差线程
校正累积误差线程接收到新的关键帧后,首先判断该关键帧的图像中是否可以检测到ArUco码。如果没检测到,则跳过此关键帧。如果该关键帧检测到ArUco码,则根据ArUco码的解码ID是否正确判断是否进行累积误差消除的工作。当ArUco码的解码ID正确时,执行位姿校正和全局地图优化,优化算法采用levenberg-marquardt[14](LM)算法。
2 累积误差消除
2.1 ArUco码检测
在建立新的关键帧时,前端跟踪线程会检测该关键帧的图像中是否存在ArUco码。检测过程如下:首先,对图像进行阈值化处理,检测出当前帧图像中所有具有凸性的候选四边形;然后,按照四边形是否相似、是否靠近边界、是否与其他四边形有包含关系等条件筛除不合适的四边形;之后,对检测到的候选四边形进行解码,辨识其ID;最后,亚像素优化ArUco码的4个顶点位置,并按照顺时针顺序将4个顶点坐标保存记录在系统中。
2.2 相机位姿估计
首先对ArUco码的坐标系进行定义,如图2所示。ArUco码的坐标系Oa-XaYaZa,坐标原点为ArUco码的中心点,X、Y轴分别为沿ArUco码的横纵线,Z轴为垂直于ArUco码表面并穿过坐标原点的直线。
本文算法的ArUco码先验信息包括两种:第一种是环境中各个ArUco码在世界坐标系的位姿Taw,第二种是ArUco码的4个3D顶点在该ArUco码坐标系中的相对位置。其中,各个ArUco码坐标系的位姿由以下方法确定:如图2所示,默认ID为0的ArUco码坐标系为世界坐标系Ow-XwYwZw,其他ArUco码坐标系的位姿即相对于该世界坐标系的位姿变换Taw。两种先验信息由人工预先标定。

图2 相机位姿估计
将第二种先验信息和2.1节中检测到的ArUco码4个顶点在关键帧图像中的亚像素位置对应,建立式(1)。
λu=KTcaP
(1)
式中,Tca是相机在ArUco码坐标系下的位姿;P是ArUco码的顶点在ArUco码坐标系下的三维坐标;u是ArUco码的顶点在像素坐标系下的对应二维坐标;K是相机的内参;λ是在相机坐标系下的深度。
4个顶点可得到4个式(1),利用EPNP算法可求解得到相机在ArUco码坐标系的位姿Tca。如图2所示,Tca为从ArUco码坐标系Oa-XaYaZa到相机坐标系Oc-XcYcZc的位姿变换。
本文中的SLAM系统根据第一种先验信息Taw及相机在ArUco码坐标系下的位姿Tca可解算出当前帧相机的位姿Tcw。解算公式如式(2)所示。
Tcw=TcaTaw
(2)
2.3 累积误差消除
校正累积误差线程会逐个关键帧地检查该帧是否检测到ArUco码。如果该关键帧没有检测到ArUco码,则跳过该帧处理下一帧;如果该关键帧检测到ArUco码时,则对其建立图模型,更新地图中关键帧的位姿信息和3D地图特征点的位置信息,消除SLAM系统的累积误差。
为了叙述方便,将检测到ArUco码的关键帧统一简洁命名为Ar帧。
2.3.1 地图预处理
在建立图模型之前首先对地图进行预处理,为图模型优化提供良好的初值,使其更快迭代收敛到最优值。
地图预处理的工作包括两部分,更新局部关键帧的位姿信息和更新局部3D地图特征点的位置信息。其中,局部关键帧是指与Ar帧有足够共视点的所有关键帧,局部地图特征点是指局部关键帧观测到的所有地图特征点。
利用2.2节得到的Ar帧消除累积误差后的位姿,更新局部关键帧的位姿信息和更新局部3D地图特征点的位置信息。
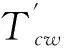

(3)

(4)
2.3.2 位姿图图模型
本文SLAM系统位姿图图模型的顶点由地图中各个关键帧的位姿构成,边由共视关键帧间的相对位姿关系构成。
各个顶点的初值按照上节关键帧被校正更新后的位姿取值。若该关键帧的位姿未在上节被更新,则按原始的位姿取值。
位姿示意图如图3所示,圆和五角星代表顶点,直线和虚线代表边。五角星顶点代表Ar帧的位姿,因其累积误差已被消除,所以令该顶点固定不变;圆顶点代表普通关键帧的位姿,为优化变量。
本文SLAM系统位姿图中的边,按照是否有Ar帧参与,可分为一元边和二元边。如图3所示,直线代表二元边,连接两个普通关键帧,构造同ORB-SLAM2中本质图的二元边一样,优化变量为两个普通关键帧的位姿;虚线边代表一元边,连接一个普通关键帧和一个Ar帧,优化变量仅有普通关键帧的位姿。满足以下条件的关键帧,其位姿相应的顶点被一元边约束:①和Ar帧是父子帧关系;②和Ar帧有足够多的共视点。
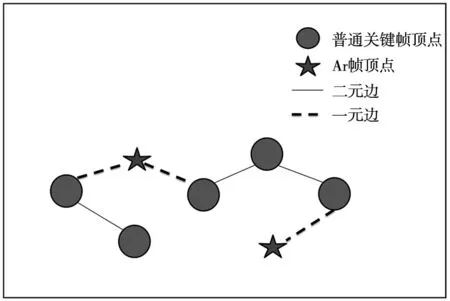
图3 位姿图示意图
位姿图中一元边的误差函数ei1如式(5)所示。其中,边的测量Tij取为局部关键帧位姿未更新前相机从Ar帧向关键帧Ki的位姿变换,Ti是Ki的位姿,Tj是Ar帧的位姿。
(5)
位姿图的误差函数Epose由所有边的误差函数相加组成,如式(6)所示。对Epose采用LM算法迭代优化,使其最小化,得到位姿图中所有顶点的最优值。
(6)
2.3.3 全局重投影误差图图模型
全局重投影误差图图模型的顶点是地图中所有关键帧的位姿和所有3D地图特征点的位置,边是3D地图特征点在关键帧图像上投影的误差。
重投影误差图模型示意图如图4所示,圆三角形和五角星代表顶点,直线和虚线代表边。五角星顶点代表Ar帧的位姿,因其累积误差已被消除,所以令该顶点固定不变;圆顶点代表普通关键帧的位姿,为优化变量。三角形顶点代表3D地图特征点位置,为优化变量。
在全局重投影误差图图模型中,边按照是否有Ar帧参与,分为一元边和二元边。如图4所示,直线边代表二元边,连接一个普通关键帧和一个3D地图特征点,其构造同ORB-SLAM2中本质图的二元边一样,优化变量为两个普通关键帧的位姿;虚线边代表一元边,连接一个Ar帧,和一个3D地图特征点,因为Ar帧位姿的累积误差已被消除,所以优化变量仅有3D地图特征点的位置。

图4 全局重投影误差图示意图
一元边对应的误差函数如式(7)所示。
(7)
式中,K是相机内参;ξj是Ar帧位姿Tj的李代数表示;Pi是3D地图特征点的世界坐标系表示;ui是该3D地图特征点在关键帧图像上匹配的二维特征点的坐标。
全局重投影误差图的误差函数Ereproj由所有边的误差函数相加组成,如式(8)所示。对Ereproj采用LM算法迭代优化,使其最小化,得到全局重投影误差图中所有顶点的最优值。
(8)
3 实验
3.1 实验条件
为验证提出的算法是否能够消除无回环场景下双目视觉SLAM产生的累积误差,在沈阳某公司的两种无回环场景下总共录制了8个数据集进行实验,分别将各个数据集命名为Dataset1-8。
两种实验场景布局图如图5所示,图5a和图5b分别对应图1中的不闭合场景和长廊场景。直线代表相机在每次录制数据时行进的大致轨迹,灰色矩形块代表该公司办公区域,为机器人的不可越过障碍物,矩形黑白色块代表ArUco码。

(a) 不闭合场景示意图 (b) 长廊场景示意图图5 实验场景布局图
以ID为0的ArUco码坐标系为世界坐标系,用米尺测量每一个ArUco码中心点在世界坐标系的X、Y轴坐标,完成对所有ArUco码坐标系位姿的预标定。米尺的最小长度单位为mm。
采集数据集所用双目相机为小觅双目相机标准版,左右目像素都是752×480像素,曝光模式采用自动曝光。实验处理算法在一台笔记本电脑上完成,电脑配置如下:CPU为Intel-i7-9750H,主频最高2.60 GHz,8 G内存,电脑操作系统软件采用Ubuntu18.04。
3.2 累积误差消除
为了检验本文系统的累积误差消除效果,分别在8个实验数据集下进行实验。因为各个实验数据集中ArUco码个数不同,为保证实验一致性,各个实验场景中都只用4个ArUco码消除SLAM系统的累积误差。在实验中,终点位置误差由米尺测量得到,最小单位为mm。为对比本文算法消除双目SLAM系统累积误差的有效性,进行了和其他优秀双目SLAM系统的对比实验。但由于数据集为自制数据集,所以选择了和典型的开源算法ORB-SLAM2(特征法SLAM主流代表)、stereo-DSO[14](直接法SLAM主流代表)和VINS_FUSION[15](光流法SLAM主流代表)进行对比实验。
在8个数据集下,分别采用ORB-SLAM2、VINS_FUSION(双目模式)、stereo-DSO和本文系统计算终点位置累积误差。统计4个SLAM系统在8个数据集下的累积误差,如表1所示。

表1 累积误差 (m)
由表1可见,在8个数据集中,相比其它杰出的双目SLAM系统,本文双目SLAM系统的累积误差都更小。
在数据集Dataset5中,其他双目SLAM系统均存在一定的累积误差,而本文双目SLAM系统的累积误差仅有0.012 m。这是因为在终点处刚刚进行了累积误差消除,使得误差值接近于0。该实验直接说明了本文累积误差消除算法的有效性。
在其余数据集中,本文SLAM系统和其他SLAM系统均存在一定的累积误差,但本文SLAM系统的累积误差远小于其他SLAM系统的累积误差。如在数据集Dataset1中,双目ORB-SLAM2系统的累积误差约为1.602 m,STEREO-DSO约为1.854 m,VINS-FUSION约为2.262 m,而本文系统的累积误差只有0.138 m。究其原因,本文SLAM系统累积误差较小,是由于采用图优化技术(graph optimization)对检测位姿和特征点的位置进行了优化的结果。这从侧面验证了本文累积误差消除算法的有效性。
3.3 系统实时性
为了检验本文系统的实时性,在8个数据集下分别进行了和双目ORB-SLAM2的耗时对比实验。在每个数据集中,记录ORB-SLAM2系统和本文系统处理每帧图像的用时。数据集Dataset1中的用时对比如图6所示。在用时图中,横轴为图像帧的序列号,纵轴为相应图像帧的花费时间。统计8个数据集下本文系统和双目ORB-SLAM2系统平均用时,如表2所示。

(a) ORB-SLAM2用时 (b) 本文算法用时图6 用时对比图

表2 单帧图片平均耗费时间 (ms)
由图6可见,本文系统和双目ORB-SLAM2系统的共同点是每帧数据处理用时都集中地稳定在30~40 ms之间,不同点在于本文系统算法处理时间的峰值比双目ORB-SLAM2系统大很多。按照对应帧数查询,发现它们的对应图像中存在ArUco码,即ArUco码检测和相机位姿估计需要多花费一部分时间。
由表2知,本文系统的平均耗时约为34.85 ms,双目ORB-SLAM2的平均耗时约为33.98 ms,本文SLAM系统平均耗时仅比ORB-SLAM2系统多0.87 ms。虽然本文增加了ArUco码检测部分,但由于其只在关键帧处检测,因而对平均耗时影响甚微。本文系统处理每帧图像用时34.85 ms,约为每秒处理28帧图像,可以满足双目SLAM系统实时性要求。
4 结束语
本文提出了一套利用ArUco码先验信息消除双目SLAM系统累积误差的创新算法。该算法由3部分组成,ArUco码检测、相机位姿估计和累积误差消除。经过在8个实验数据集下实验测试,证明本文提出的算法,可以稳定可靠地消除双目SLAM系统的累积误差,同时满足机器人定位的实时性要求。
在实际应用本文提出的SLAM系统时,发现虽然可以解决累积误差问题,但视觉SLAM系统有时仍然不能正常工作。究其原因,是实验场景中的特征在一些局部区域内非常少,如柱面、墙面等,导致系统无法提取到足够的特征,不足以估计相机位姿和建立新的地图特征点。因此,本文的下一步工作将会向融合点线面特征等方向发展,用以解决弱纹理区域定位困难的问题。

