基于AGA的焊接机器人避障轨迹规划*
张 宏,汤小红,2,龚永健,任垒垒
(1.中南林业科技大学机电工程学院,长沙 410004;2.湖南理工学院机电工程学院,岳阳 414000)
0 引言
随着智能制造的大规模发展,机器人技术在工业领域得到了广泛的应用,其中机器人的运动规划与避障问题是当前的研究热点。机器人路径规划的主要任务是找到从初始构型到最终构型的最优无碰撞轨迹。近年来,许多专家学者针对这个问题进行了深入的分析和研究。CHEN等[1]在改进自抗扰控制的基础上,提出了一种高精度的自由度串联机器人轨迹跟踪控制策略,利用运动学方程和速度逆雅可比矩阵将运动轨迹和姿态轨迹转换为关节轨迹来完成任务空间轨迹的跟踪控制,实现了位置和姿态轨迹跟踪精度的提高。HUANG等[2]采用全局遗传方法规划受关节速度、角度、力矩和加速度约束的机器人运动轨迹。SUDHAKARA等[3]提出了一种对现有的A-star算法进行改进的优化技术,用于机器人在不碰撞任何障碍物的情况下,确定从起始状态到目标状态的最佳路径。ZHANG等[4]提出了一种基于实时优化的串行机器人轨迹规划方法,将原来的联合耦合优化问题转化为多个联合独立优化问题,计算复杂度大大降低,有效的提高了优化求解的计算效率。RÖSMANN等[5]提出了一种新的基于拓扑特征的移动机器人轨迹在线优化集成方法,通过最小化路径长度、过渡时间等目标来改变由全局规划器生成的初始粗路径。王志强[6]针对并联机器人的插补算法和轨迹优化问题,研究了一种基NURBS的Delta机器人时间最优轨迹优化算法,并在三维环境下验证了算法的性能。实验结果表明,该算法能够充分发挥并联机器人的性能,满足其运行平稳、高速、准确的指标。CHEN等[7]采用点云切片技术通过激光扫描获得待喷涂工件的点云数据进而进行处理,利用插补算法连接数据点,得到喷涂机器人的空间轨迹。SHINTAKU[8]提出了一种以能量最小为优化目标的遗传算法,并通过确定多项式的参数来最小化目标函数的适应度。PACK等[9]针对空间中存在障碍物轨迹规划问题,提出了一种基于遗传算法的构型空间有效解搜索方法。YANO等[10]应用遗传算法求解两关节机器人手臂末端执行器的位置和运动。定义了笛卡尔空间和关节空间的目标函数,组合起来优化机器人的轨迹,获得了光滑轨迹和最小关节旋转的最优解。
尽管当前机械臂轨迹规划方法与相关的研究成果很多,但基本是不同学者根据不同的实际应用与生产需求进行的针对性研究,到目前为止也未形成完整的轨迹规划体系;目前,围绕焊接机器人的光滑焊缝轨迹规划,最小能量、最小时间、最小冲击等轨迹优化方法的研究逐渐被提上日程,成为学术界的研究热点之一。
针对经典遗传算法进行优化选择时易困于空间局部最优解的缺点,本文以ABB IRB 120焊接机器人为研究对象,采用自适应遗传算法(AGA)优化机器人在避开障碍物进行焊接工作时的路径。该算法设计含有惩罚项的适应度函数,降低不满足运动学约束条件的个体被选择的概率;自适应调整交叉概率Pc和变异概率Pm,加快算法收敛速度,找到起始位置到目标点的路径,保证机器人在运动过程中不与障碍物相撞,从而使得末端执行器能在避开障碍物的前提下寻找到最优路径。
1 机械臂运动学系统建模
为描述机械臂连杆间的几何关系,国内外学者做了大量的研究,目前已经有多种成熟的方法。本文采取D-H法[11]建立空间机械臂运动学模型,该方法的优点是涉及参数较少,模型一致性较好。
D-H法是机器人运动学分析中最常用也是最为经典的建模方法,该方法通过一系列规则建立机械臂连杆坐标系,采用αi、ai、di、θi(i=1,2,…,n)等4个变量来描述空间机械臂连各杆间的变化关系。其中,αi为关节i与关节i+1轴线的夹角,称为连杆i的扭角;ai为关节i和关节i+1轴线的公垂线的长度,称为连杆i的长度;di为关节i轴线上两公法线之间的距离,称为关节i的偏置;θi为关节i轴线方向上两公法线之间的夹角,称为关节i的转角。
αi和ai为连杆i的参数,用于描述连杆i本身;di和θi为关节i的变量,用于描述连杆i和连杆i+1间的关系。对于旋转关节,di是固定不变的,θi随关节运动而变化;对于移动关节,θi是固定不变的,di随关节运动而变化。
在此6R焊接机械臂的运动学分析中,将连杆从机械手的基座到末端执行器依次编号为0,1,2,…,n。将连杆i-1与连杆i组成的运动副记作第i个关节,这样机械臂可以看作是由n+1个连杆和n个关节组成[12]。采用坐标后置法建立坐标系,在机械臂基座处以O0为坐标原点建立第一个坐标系,将关节1的坐标系与基坐标系重合。根据D-H法则依次建立其他关节坐标系,将中间坐标系O1、O2、O3、O4、O5分别设在关节2、3、4、5、6处,将工具坐标系O6建立在执行器末端点处。最终得到机械臂的连杆坐标系如图1所示,此焊接机器人的D-H参数如表1所示。

图1 6R焊接机器人连杆坐标系

表1 连杆参数表
2 机械臂运动学分析
2.1 正运动学分析
对于机械臂而言,其正运动学问题是在已知基座位姿和关节角时,解算其末端位姿的过程。根据D-H法,可得连杆坐标系{i-1}与连杆坐标系{i}之间的变换矩阵为[13]:
(1)
(2)
令s表示sin,c表示cos,此后一律采用此约定。将表1中的数据带入式(2)得该焊接机器人各相邻连杆的变换矩阵如下:
将各个变换矩阵依次相乘得到其末端执行器坐标系相对于机座坐标系的变换矩阵为:
(3)
式(3)矩阵中的前三列表示该焊接机器人末端执行器在基坐标系下的姿态,最后一列表示该焊接机器人末端执行器在基坐标系下的位置。
将表1中的数据代入式(3)得:
(4)
图2是利用MATLAB/Robotics Toolbox建立的焊接机器人三维数学模型,其位置和姿态与式(4)所求结果完全相同,表明此焊接机器人运动学方程是正确的。
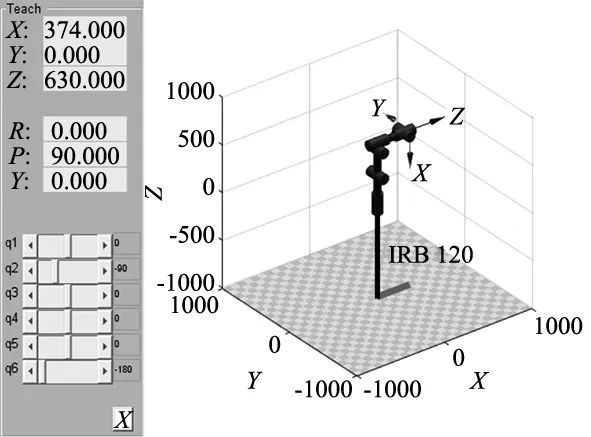
图2 焊接机器人MATLAB仿真模型
2.2 逆运动学分析
将末端执行器的位置和姿态从笛卡儿空间变换到关节空间的过程定义为运动学逆问题。本文所研究的ABB IRB 120六自由度焊接机器人后3个关节的轴线交于一点,根据机器人求封闭解的条件,该焊接机器人的逆运动学分析有封闭解[14]。
本文基于代数法,采用位姿分离的方法简化求解过程,得到该焊接机器人的逆解。但该解析结果并不唯一,需要从所得出的所有解析结果中选择一组最优解。
记该机器人后3个关节轴线交于腕心,在式(3)中,令d6=0,可得腕心的坐标x、y和z分别为:
wx=302cθ1cθ23+70cθ1sθ23+270cθ1sθ2
(5)
wy=302sθ1cθ23+70sθ1sθ23+270sθ1sθ2
(6)
wz=-302sθ23+70cθ23+270cθ2+290
(7)
进而可得:
(8)
利用式(8)将连杆坐标系{6}以原姿态置于腕心,将该焊接机器人的逆运动学求解问题从末端转换到腕心。为提高计算效率,采用位姿分离的方法,根据腕心的位置得到θ1、θ2与θ3,再根据腕心的姿态解算出后3个关节角。
2.2.1 解算前3个关节角
联立式(5)和式(6)可得:
wxsinθ1-wycosθ1=0
(9)
由式(9)得:
(10)
联立式(5)、式(6)和式(7)可得:
Asθ2+Bcθ2=E
(11)
(12)
式中,A=wxcθ1+wysθ1;B=wz-290;E=(A2+B2+2702-702-3022)/540;G=A-270sθ2;H=B-270cθ2。
由式(11)求解得:
(13)
由式(12)和式(13)求得:
θ3=atan2(70G-302H,70H+302G)-θ2
(14)
2.2.2 解算后3个关节角
连杆坐标系{3}与{6}之间的姿态变换矩阵为:
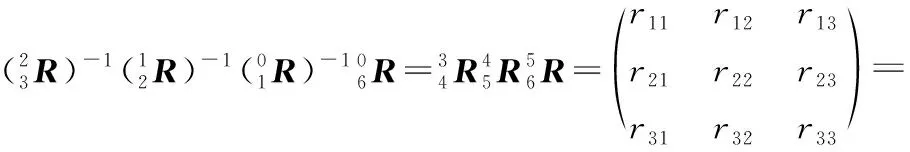
(15)
由式(15)可得:
(16)
θ4+θ6=atan2(r12,-r22)
(17)
此时,关节4和关节6的轴线重合,机器人处于奇异位形,可以适当选取θ4的值,然后由式(16)得到相应θ6的值。
当θ5≠0时,由式(15)得:
θ4=atan2(-r23/sθ5,-r13/sθ5)
(18)
θ6=atan2(-r32/sθ5,-r31/sθ5)
(19)
根据θ6的关节范围以及机器人实际作业情况,取(-180°,180°]。
3 自适应遗传算法轨迹优化设计
3.1 优化问题描述
针对焊接机器人在焊接过程中,末端执行器需要穿过障碍物内部或者需要避过特定形状的障碍物进行焊接时,机械臂与障碍物之间的干扰影响焊接质量与焊接效率。本文以矩形框障碍物为例,通过分析机械臂与障碍物之间的位置关系,将机械臂和障碍物进行简化之后再进行空间几何位置分析,从而简单快速地判断出机械臂在工作时是否和工作空间中的障碍物发生碰撞。
自适应遗传算法(AGA)可以根据适应度自动改变交叉概率Pc和变异概率Pm。当种群的个体适应度为局部最优时,这两个参数会增大,但当种群适应度分散时,这两个参数会减小。同时,当种群的适应度平均值较为靠近最大适应度值时,自适应地减小Pc,同时增加Pm, 以便更好地产生新的个体摆脱局部极值寻找到全局最优解[15-17],进一步提高收敛速度与寻优能力,保持种群的多样性,缩短运行时间。
机械臂在运动过程中,每个关节的关节扭转角、关节速度和关节加速度直接影响着机械臂的运动结果,因此本文将其作为遗传算法的优化参数,进行避障轨迹规划。以ABB IRB 120机器人为研究对象,通过在机器人末端添加焊接头实现焊接工作。优化过程采用的适应度函数为:
fG=fob/(η1f1+η2fq+η3ft)
(20)
式中,fG为适应度值;η1、η2、η3为加权系数;f1为机械臂末端执行器运动过的路径长度;fq为各关节的关节角增量之和;ft为路径上运动的总时间。
f1的求解:在进行轨迹规划的时候设机器人的实时中断周期为t,总的运动时间为T1+T2,对于其中的一个障碍点来说,前后两段之间的周期数为t/T1、t/T2,每个周期末端执行器的位置坐标之间的距离就是执行器走过的路径长度。
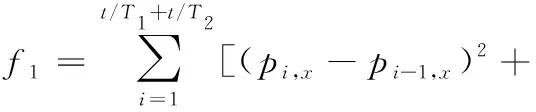
(21)
式中,p为每个周期对应的末端执行器的位置。关节角增量fq计算如下:
(22)
式中,pij为第i个周期的第j个关节角度值。
通过简化计算,当点和线段距离大于指定距离时,fob=1,否则fob=0。
3.2 实验仿真平台
3.2.1 遗传算法仿真分析
本文选取初始种群为P=100,进化代数G=400。 障碍物简化为矩形框,路径优化结果分析如图3所示。
从图3中种群适应度值的变化趋势可以看出自适应遗传算法在0~54代之间适应度值呈迅速上升趋势,54代后虽有极小范围内的波动,但整体收敛,其最大种群适应度值达到1.544 6。在同样参数下,采用经典遗传算法得到的种群适应度值得变化趋势。从图中可以看出,经典遗传算法在进化到70代时才开始收敛,收敛时间较长;且收敛后,其种群适应度值波动较大,容易陷入局部最优解。
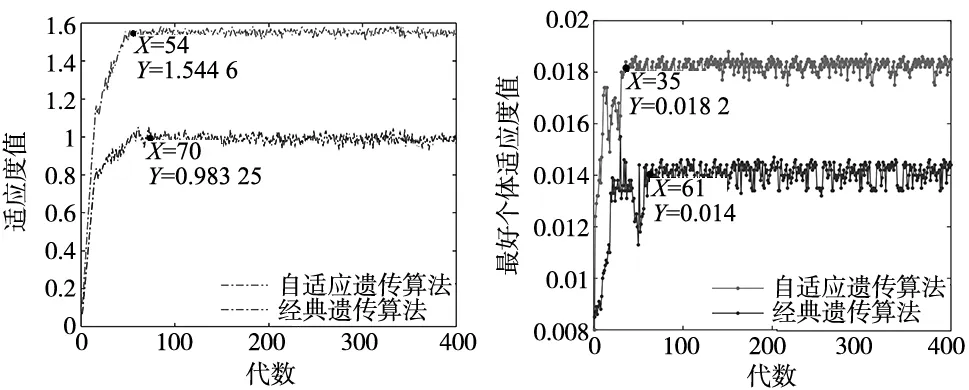
图3 自适应遗传算法与经典遗传算法种群适应度 图4 自适应遗传算法与经典遗传算法最好个体适应度
通过对比两种算法种群适应度变化趋势可以看出,自适应遗传算法的收敛性明显好过经典遗传算法;且最大适应度值高于经典遗传算法所得的最大适应度,在遗传的过程中可以保持种群中个体基因的多样性;通过自适应遗传算法进行优化选择时不易困于空间中的局部最优解。
图4为自适应遗传算法与经典遗传算法最好个体适应度值随进化代数增加的变化趋势,由图可知,自适应遗传算法从第35代最好个体适应度值开始收敛,随进化代数增加逐渐趋于稳定,稳定值为0.018 2,虽有小范围内浮动,但整体收敛性较好。而经典遗传算法得到的最好个体适应度在上升过程中发生突变,但随进化代数的增加,在第61代时收敛,收敛后仍有上下波动,相比自适应遗传算法,波动幅度较大;优化选择的最好个体适应度为0.014,同样最优个体收敛时间较自适应遗传算法长,计算效率偏低。
通过对比分析可得,自适应遗传算法的个体明显优于经典遗传算法。所以通过自适应遗传算法进行优化选择时能够较好的在全局空间中去寻找最优解。
3.2.2 五次多项式插值轨迹规划仿真分析
机器人在焊接过程中,从当前焊点位姿向下一个焊点位姿进行调整的过程中,需要保持焊钳的平滑过渡,在此过程中,机器人关节变化不稳定会引起焊钳抖动,进而影响焊钳的状态,对焊点质量产生影响。因此,本次优化设计为满足加速度条件使运动轨迹保持连续性和平滑性,使用五次多项式插值进行轨迹拟合,生成相对平滑的各关节角位移、角速度及角加速度曲线,实现焊接机器人平稳、精确地穿过障碍物的运动。五次多项式通式为:
θ(t)=a0+a1t+a2t2+a3t3+a4t4+a5t5
(23)
式中,a0、a1、a2、a3、a4、a5为待定系数。
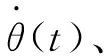
(24)
由此可获得五次多项式插值下的关节运行路径函数。在MATLAB编辑框中,输入起止位置q、起止时间、起止速度以及起止加速度。并设定初始状态。得到的各个关节角、角速度、角加速度变化趋势图以及机械臂规划后的路径图如图5所示。

(a) 机械臂穿过障碍物所扫过的路径 (b) 机械臂在YOZ平面的路径投影
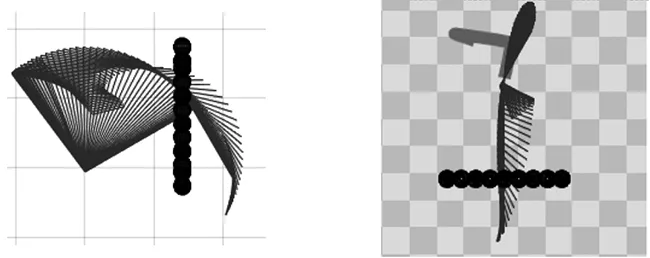
(c) 机械臂在XOZ平面的路径投影 (d) 机械臂在XOY平面的路径投影图5 自适应遗传算法规划轨迹
其为通过MATLAB/Robotics Toolbox编程获得焊接机器人在笛卡尔空间中的运动轨迹。由以上结果可以看出,通过自适应遗传算法优化选择后的路径能够顺利平滑的穿过障碍物,很好的从起始点出发达到目标点。
图6~图8分别为基于五次多项式插值所得该焊接机器人关节角、关节角速度、关节角加速度变化曲线图。从图6可以看出,焊接机器人焊枪末端在运行过程中一直保持连续平稳,验证了正逆运动学求解的准确性。从图7与图8中可以观察到,各关节角速度、角加速度初始和终止点的值都是0,满足设置的初始条件;各关节速度整体波动的大小在(-2,2)之间,远小于关节设置的速度约束;关节角加速度曲线连续,整个运动过程变换缓和,无突变现象发生。由此可见,该焊接机器人在焊接过程中机构运行平稳,且各连杆之间无错位冲突现象,不会产生较大震动,焊接质量更为可靠。
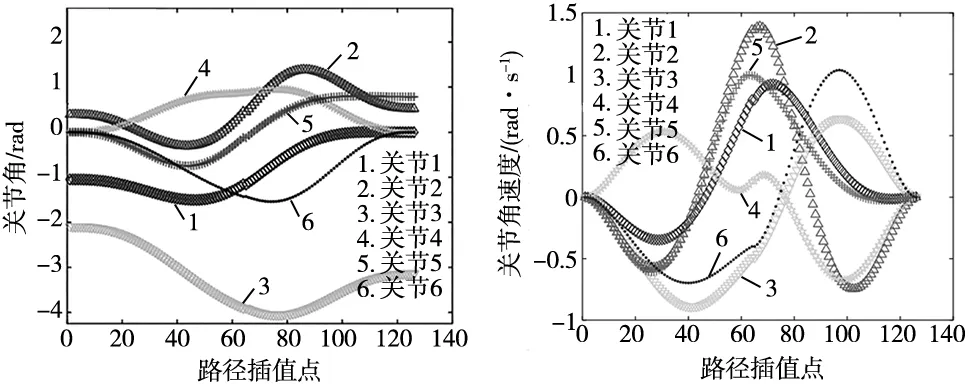
图6 各关节角变化 图7 各关节角速度变化
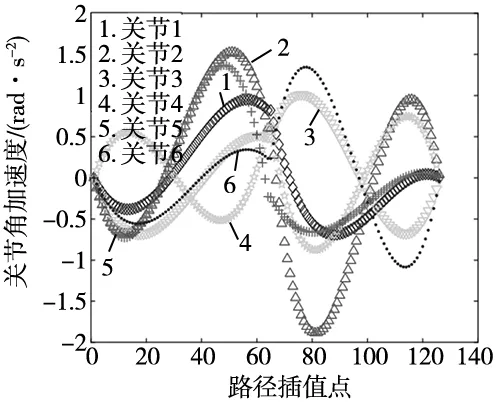
图8 各关节角加速度变化
4 结论
本文以ABB IRB 120焊接机器人本体为基础,建立其数学模型。采用自适应遗传算法规划焊接机器人末端执行器顺利穿过障碍物的最优轨迹;同时基于五次多项式对关节角进行约束规划,从而使得焊接机器人在工作的过程中不仅能够避免与障碍物碰撞;其关节角、关节角速度、关节角加速度都可以连续平滑的过渡,保证机械臂的运动稳定性,有效的防止了运动过程中受力过大造成机器或焊接件的损坏。通过MATLAB/Robotics Toolbox仿真结果表明,与经典遗传算法相比,自适应遗传算法(AGA)在进化的时候不容易发生“早熟”现象,有效地减少轨迹运行时间,提高机器人的工作效率;且在焊接机器人通过目标路径点的过程中能以平稳的速度曲线、较小的加速度和较小的运动时间行走,可以快速地找到机械臂在运动过程中的最优路径。

